在复变函数教学中加强对解题方法的归纳和总结

李景和，周永芳，李艳玲，白云

在复变函数教学中加强对解题方法的归纳和总结

李景和，周永芳，李艳玲，白云

（河北工业大学 理学院，天津 300401）

针对学生在复变函数学习中对解题方法掌握不佳的实际情况，归纳和总结了３种常见题型的解题方法，并予以分析和说明. 通过加强对解题方法的归纳和总结，以期提高学生的解题能力，加深学生对教学内容的理解和掌握，从而收到良好的教学效果．

解题方法；可导性；复积分；孤立奇点；归纳和总结

复变函数是大学工科许多相关专业的基础课，在工科复变函数的教学实践中，经常发现一些学生对解题方法掌握不佳，做题无从下手．在教学中加强对解题方法的归纳、总结和分析是十分必要的，这将有助于学生消化和吸收所学的知识，改善学生做题无从下手的状况，从而提高该课程的教学效果．本文以复变函数可导性的判定、求复积分的值和孤立奇点类型判定这３种常见题型为例，对解题方法进行归纳、总结和分析.

1　复变函数可导性的判定方法

复变函数可导是复变函数中十分重要的概念，函数可导性的判定与函数解析性的判定密切相关，一般来说，可导性的判定有３种方法．

1.1　由复变函数可导的定义进行判定

1.2　由复变函数求导法则和复变初等函数可导性讨论的结论进行判定

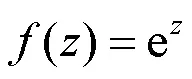
1.3　由复变函数可导的充要条件定理进行判定

1.4　判定复变函数可导性３种方法的说明和分析

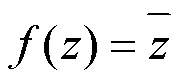
2　求复变函数积分的方法

教材[1]有“复变函数的积分”一章，在这章学完后，可根据教材全章的例题和作业题，对这一章中求复积分的方法进行总结，一般有3种常用的方法[8]：

2.1 原函数法

2.2 求闭路积分的方法

2.3　应用基本公式

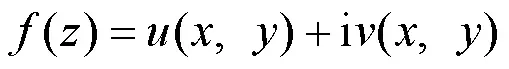
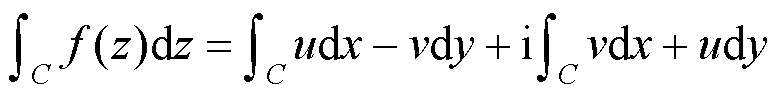
2.4　求复变函数积分3种方法的说明和分析

（4）需要特别指出的是，在求复积分时，由于被积函数往往形式多样，有时会比较复杂，必要时可适当变形，综合运用定理和积分的性质等所学知识，如可将被积函数拆分为若干分式的代数和，利用已经推出的一些例题的结论等．另外，教材[1]在一个用多种方法求解积分的例题中，其中一个方法是由复积分的定义求得复积分，但在实际做题时，一般很少采用由定义求复积分，因此此种方法没有总结在常见方法之中．

3　复变函数孤立奇点类型的判定方法

3.1　展开式法

3.2　极限法

3.3　拆分变形法

3.4　取倒转零法

3.5　分子分母零点阶数比较法

3.6　判定孤立奇点类型５种方法的说明和分析

（1）展开式法对判定３种孤立奇点都是适合的，尤其是对本性奇点的判定，展开式法应是最佳选择．

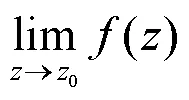
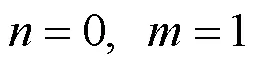
（5）由于函数形式的多样性，因此实际做题时到底用哪种方法还要结合函数的具体特点，有的孤立奇点的判定适合多种方法，应选择最快捷简便的方法进行判定．

4　结语

对解题方法进行归纳、总结和分析，既可以穿插在教学内容之中，也可在习题课上复习时统一进行，应随时给学生布置总结解题方法的作业，调动学生积极思考，以加深学生对解题方法的掌握．

在教学中加强对常见题型解题方法的归纳和总结，在一定程度上提高了学生解题的能力．教学的实践表明，对一些常见题型的解题方法进行认真总结和详细分析，有利于改善学生做题无从下手的状况，对学生消化相关的教学内容，提高课程的教学效果起到良好的促进作用．

[1] 徐勇，李景和，张相梅．复变函数与积分变换[M]．北京：科学出版社，2018：24-25，43．

[2] 西安交通大学高等数学教研室．复变函数[M]．4版．北京：高等教育出版社，1996：37，97-98．

[3] 王锦森．复变函数[M]．北京：高等教育出版社，2008：37．

[4] 徐永权．工程数学[M]．天津：天津科学技术出版社，1996：415-416．

[5] 钟玉泉．复变函数论[M]．4版．北京：高等教育出版社，2013：49．

[6] 白艳萍，雷英杰，杨明．复变函数与积分变换[M]．北京：国防工业出版社，2004：20-21．

[7] 王志勇．复变函数与积分变换[M]．2版．武汉：华中科技大学出版社，2017：15．

[8] 陆庆乐．复变函数学习方法指导书[M]．北京：高等教育出版社，1982：79．

Strengthening the induction and summary for the solution method in teaching of complex function

LI Jinghe，ZHOU Yongfang，LI Yanling，BAI Yun

（School of Science，Hebei University of Technology，Tianjin 300401，China）

For the actual situation that students do not grasp the solution method well in learning of complex function， the solution method of three common question types was induced and summarized，then the analysis and explanation was given．By strengthening the induction and summaryfor the solution method，hope to improve students' problem-solving ability，deepen students' understanding and mastery for teaching content，so as to receive good teaching effect .

solution method；derivability；complex integral；isolated singular point；induction and summary

1007-9831（2022）09-0070-05

O174.5∶G642.0

A

10.3969/j.issn.1007-9831.2022.09.015

2022-01-07

河北工业大学2020年度本科教育教学改革研究与实践项目（202003004）

李景和（1963-），男，天津人，副教授，从事工科数学教学研究．E-mail：limu1987@yeah