一类有理函数的拐点问题
2022-10-20万安华
万安华
一类有理函数的拐点问题
万安华
(中山大学 数学学院,广东 广州 510275)
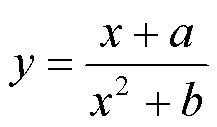
有理函数;拐点;二阶导数;一元三次方程解法;变量替换
拐点在刻画函数曲线的凹凸性时具有重要的作用[1-7].已有文献中有一些关于多项式函数的拐点个数的研究[8-10],但未见对有理函数的拐点问题进行系统研究的文献.

图1 曲线与3个拐点所在的直线



类似地,可以得到式(2). 证毕.
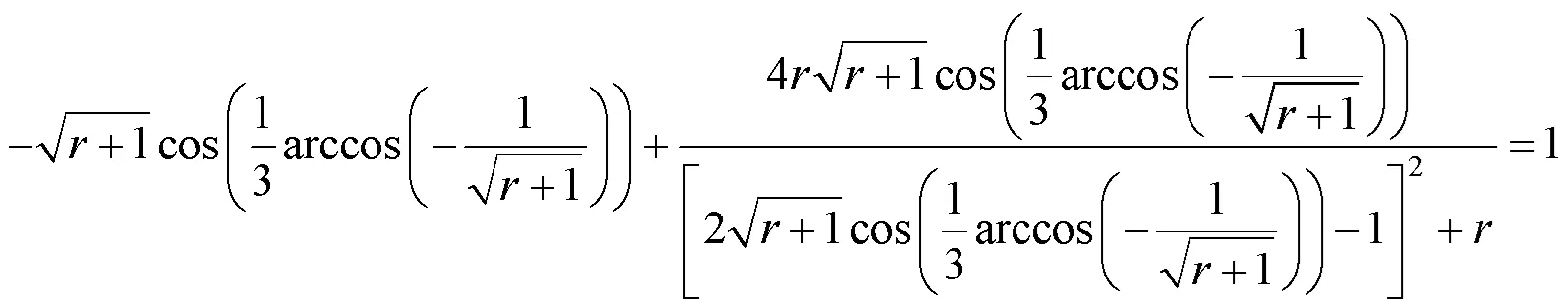



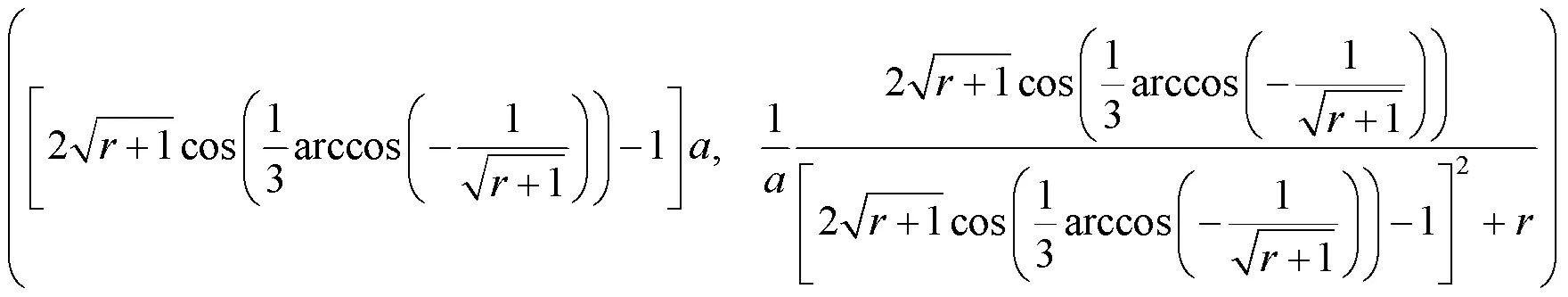
由引理1可知,3个拐点共线,共同所在直线的斜率为

由此,曲线的3个拐点所在直线的方程为

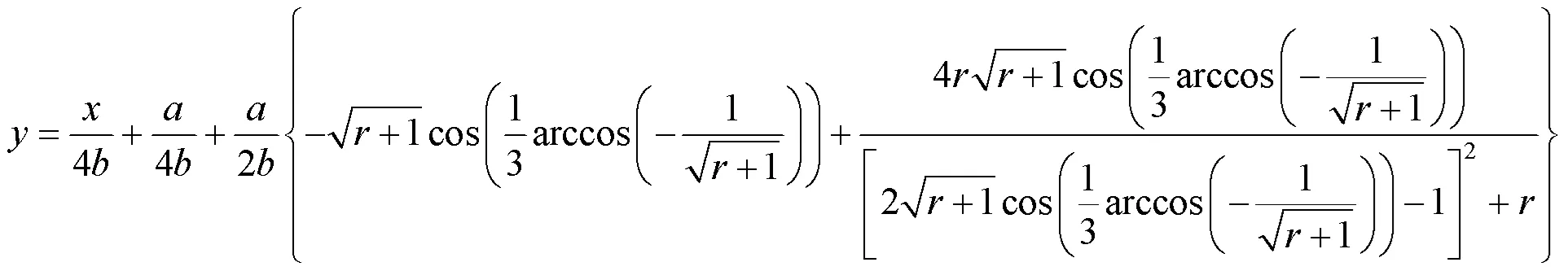

图2 和3个拐点所在的直线
综合定理1~2,可得到定理3.
3 结语
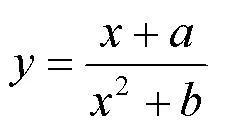
[1] 同济大学数学系.高等数学:上[M].7版.北京:高等教育出版社,2014.
[2] 同济大学数学系.高等数学习题全解指南:上[M].7版.北京:高等教育出版社,2014.
[3] 李忠,周建莹.高等数学:上[M].2版.北京:北京大学出版社,2009.
[4] 王绵森,马知恩.工科数学分析基础:上[M].3版.北京:高等教育出版社,2017.
[5] 朱健民,李建平.高等数学:上[M].2版.北京:高等教育出版社,2015.
[6] James Stewart.Calculus[M].8th ed.Boston:Cengage Learning,2015.
[7] Joel Hass,Christopher Heil,Maurice D.Thomas′ Calculus[M].14th ed.Boston:Pearson,2018.
[8] 易良海,齐紫微,林敏,等.一类特殊函数的拐点的计数方法[J].高等数学研究,2017,20(5):25-27.
[9] 倪谷炎,李颖.多项式函数的极值点与拐点判别及个数公式[J].高等数学研究,2016,19(5):7-9.
[10] 明万元,黄香蕉.一种判断多项式函数极值点和拐点个数的简单方法[J].大学数学,2011,27(6):161-163.
The inflection points of a class of rational functions
WAN Anhua
(School of Mathematics,Sun Yat-sen University,Guangzhou 510275,China)

rational function;inflection point;second derivative;solving method of univariate cubic equation; variable substitution
1007-9831(2022)09-0001-07
O171
A
10.3969/j.issn.1007-9831.2022.09.001
2021-12-20
广东省高等教育教学改革建设项目(2021);广东省教育科学规划课题(2021GXJK167);广东省自然科学基金项目(2020A1515010454);广州市科技计划项目(201904010374);中山大学本科教学质量与教学改革工程项目(2021)
万安华(1976-),女,江西南昌人,副教授,博士,从事优化、稀疏信息处理研究.E-mail:wananhua@mail.sysu.edu.cn
