有限元方法计算格式的向量化

何朝葵

有限元方法计算格式的向量化

何朝葵

（河海大学 理学院，江苏 南京 211100）

针对初学者反映有限元方法难以编制程序的问题，基于Python软件的向量运算优势，引入形函数向量和形函数导数向量，从而使有限元方法的计算格式向量化．向量化后的计算格式简单易懂，易于编写程序，也便于根据精度要求和边界条件的变换进行调整.

有限元方法；高斯积分；向量化；程序

有限元方法是一种非常流行的数值计算方法，广泛应用于结构力学、流体力学和热学等众多领域．掌握有限元方法已成为很多工程设计从业人员的一个基本要求．有限元方法由于其具有理论性强、基础要求高、实践应用性特别强的特点，给有限元方法课程教学的内容安排、教学方案设计带来了很大的挑战，学生普遍反映学习的难度大，为此，众多学者对有限元方法课程如何选择教材，如何安排教学内容，采用何种有效教学手段进行了深入的探讨[1-8]．有限元方法课程一个关键的难点在于有限元方法的计算格式比较繁杂，导致程序的编写比较困难，而学生判断“懂了”和“没懂”的关键指标就是程序编制是否成功，一旦程序调试成功，他们才认为掌握了有限元这种方法．在有限元方法课程教学过程中，教师不妨把教会学生编制有限元方法程序（一次插值和二次插值）作为首要任务，再思索如何简明地讲解有限元方法计算格式，引导他们编制相应的程序．

1 有限元方法计算格式

有限元方法的第一步，基于加权余量原理把问题的微分形式转化为积分形式．如对于两点边值问题

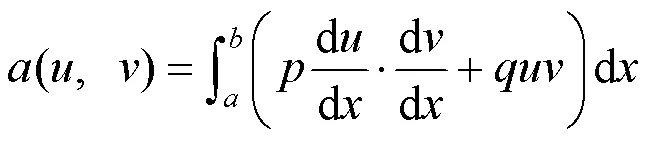
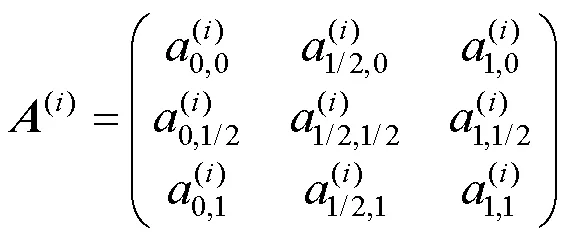
其中

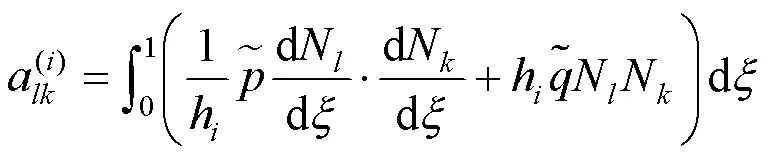
（7）

按照有限元方法这个计算格式的流程，把关键点放在式（6）（7）上，采用循环语句依次对每个单元计算单元的系数矩阵和常数项矩阵里的每一个元素，并且积分还要采用高斯积分，这样就需要多个循环语句．另外，由于3个形函数和形函数的导数的结构是不同的，程序编写起来就会很冗长，对于初学者来说，编制程序就变得非常困难．第一次讲授时，20个学生中只有3个学生编制程序成功．这严重地影响了教学的效果．因此，如何优化有限元方法的计算格式，使其便于初学者理解，并易于编制程序就显得非常重要．

2 计算格式向量化

考虑到Python软件的向量运算功能，对有限元方法计算格式采用向量形式来表示，引入形函数向量和形函数导数向量

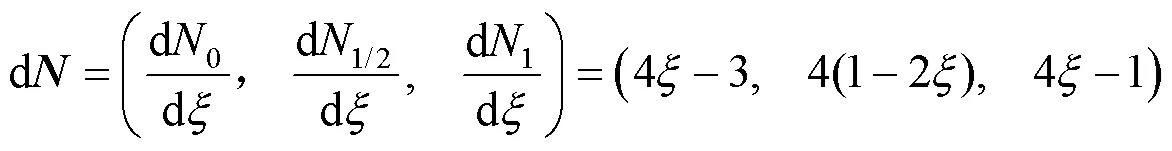
那么，单元系数矩阵和单元常数项矩阵就可分别表示成

结合高斯积分

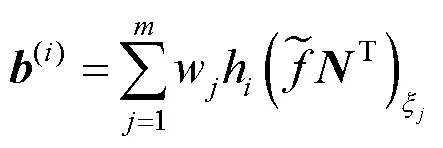
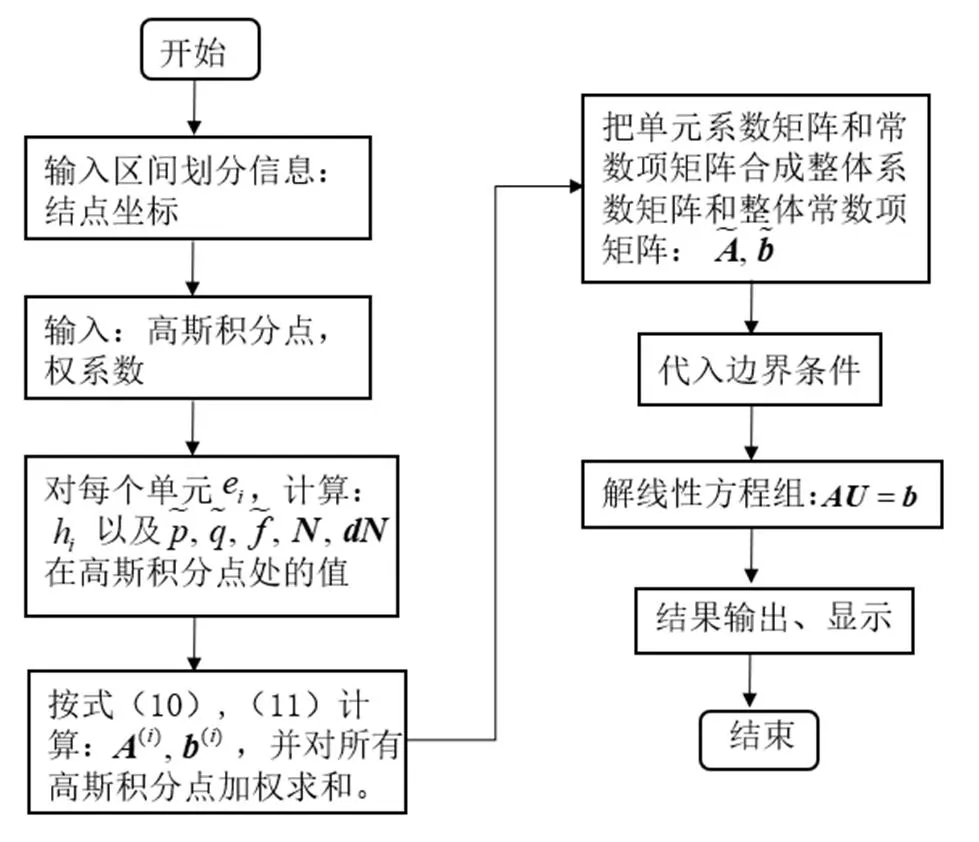
图1　有限元方法程序流程

3 有限元方法程序

1 import numpy as np

2 x=[0，0.45，1，1.5，2]

3 n=len（x）

4 m=2；n1=m*（n-1）+1；

5 xi=[0.2113，0.7887]

6 w=[0.5，0.5]

7 n2=len（w）

8 c1=1；c2=8

9 A=np.zeros（（n1，n1））；h=np.zeros（n-1）

10 b=np.zeros（（n1，1））

11 for i in range（n-1）：

12 h[i]=x[i+1]-x[i]

13 Ai=np.zeros（（m+1，m+1））

14 bi=np.zeros（（m+1，1））

15 for j in range（n2）：

16 p=x[i]+h[i]*xi[j]+1

17 q=1

18 f=x[i]+h[i]*xi[j]

19 N=[[（2*xi[j]-1）*（xi[j]-1），4*xi[j]*（1-xi[j]），xi[j]*（2*xi[j]-1）]]

20 dN=[[4*xi[j]-3，4-8*xi[j]，4*xi[j]-1]]

21 NT=np.transpose（N）； dNT=np.transpose（dN）

22 Ai=Ai+w[j]*（p/h[i]*np.dot（dNT，dN）+h[i]*q*np.dot（NT，N））

23 bi=bi+w[j]*f*NT*h[j]

24 A[m*i：m*（i+1）+1，m*i：m*（i+1）+1]=A[m*i：m*（i+1）+1，m*i：m*（i+1）+1]+Ai

25 b[m*i：m*（i+1）+1]=b[m*i：m*（i+1）+1]+bi[0：m+1]

26 A[0，：]=0.0；A[0，0]=1；b[0]=c1

27 A[n1-1，：]=0.0；A[n1-1，n1-1]=1；b[n1-1]=c2

28 invA=np.linalg.inv（A）

29 u=np.zeros（（n1，1））

30 u=np.dot（invA，b）

31 y = np.zeros（（n1，1））

32 for i in range（n-1）：

33 y[m*i]=x[i]

34 for k in range（m-1）：

35 y[m*i+1+k]=x[i]+（k+1）*h[i]/m

36 y[n1-1]=x[n-1]

盐城地区年平均日太阳辐照量达13 582kJ/m2，全年大部分时间太阳光照充分，6层商业裙房屋顶面积大，除放置机电各专业机房及设备，太阳能集热板布置条件好。

37 u2 = np.zeros（（n1， 2））

38 u2[：，0]=y[：，0]； u2[：，1]=u[：，0]

39 print（u2）

程序的第5，6行是高斯积分点以及对应的权系数，计算单元系数矩阵和单元常数项矩阵只用了2行代码，即第22，23行．第19，20行分别为形函数向量、形函数导数向量，如果要采用更高次的拉格朗日插值函数，则修改第19，20行，并相应地提高数值积分的精度，修改程序的第5，6行，以及第4行中的m即可．程序具有良好的可读性，根据精度需求和不同的边界条件易于做出相应的调整.

4 应用实例

例1边值问题

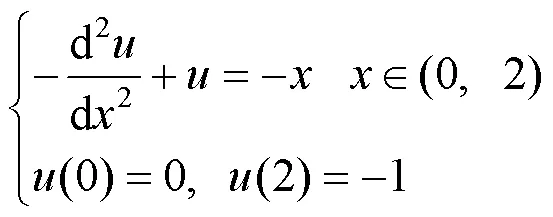
图2　例1的有限元方法数值解

例2 混合边值问题

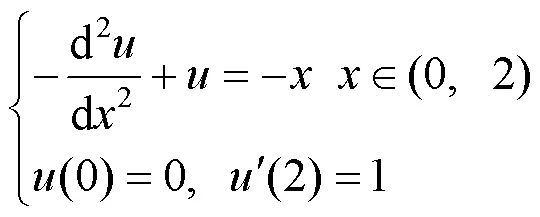
由边界条件有，因此，在对例1采用三次插值函数计算的基础上再修改程序中第8，27行：8 c1=0；g=1；27 b[n1]= b[n1]+1．运行程序，得到数值解（见图３）．

5 结语

有限元方法程序主要步骤在于依次对每个单元计算单元系数矩阵和单元常数项矩阵，经典的有限元方法教材编制程序用的是Fortran语言，通过多个循环语句来计算单元系数矩阵和单元常数项矩阵的元素，这可以理解为从微观的角度来编制程序．借助Python语言矢量运算的优势，引入形函数向量和形函数导数向量，那么单元系数矩阵和单元常数项矩阵就是通过向量运算得到的，即是从宏观的角度来理解有限元方法的计算格式，从宏观的角度来编制程序，程序不但具有良好的可读性，还便于根据精度要求、边界条件的变换进行调整，这显然达到了优化程序的目的．由于篇幅的限制，本文是以一维问题为例来说明向量化的优势，实际上对于二维、三维问题这一优势更加明显．把计算格式向量化后，在教学实践中也看到了效果，编制程序成功的学生越来越多，选这门课的学生也越来越多．

[1] 刘岩．专业认证背景下有限元技术基础课程改革与实践[J]．高师理科学刊，2019，39（4）：76-79．

[2] 周腾，吴之豪，史留勇．有限元分析及混合教学法在材料力学课程中的教学研究[J]．高教学刊，2021（35）：82-86，90．

[3] 马竹樵．应用型本科院校《有限元方法》教学改革分析[J]．教育现代化，2019，6（15）：51-53．

[4] 刘杨，赵宇来，奚方权，等．有限单元法课程教学现状与改革方法探究[J]．中国教育技术装备，2019（18）：71-73．

[5] 于亚婷，杜平安．《有限元法》课程实践教学方法探索[J]．实验科学与技术，2008（1）：108-110．

[6] 智晋宁．有限元方法课程教学改革与实践[J]．安徽工业大学学报（社会科学版），2010，27（5）：117-118．

[7] 张有宏，常新龙，张青，等．基于“理论引领、应用并行、案例示范”理念的有限元方法教学改革与实践[J]．教育教学论坛，2020（6）：127-128．

[8] 向家伟．“有限元方法及程序设计”课程教学实践[J]．重庆工学院学报（自然科学版），2007（7）：171-173．

[9] 林群．微分方程数值解法基础教程[M]．3版．北京：科学出版社，2017．

[10] 章本照，印建安，张宏基．流体力学数值方法[M]．北京：机械工业出版社，2003．

Vectorization of calculation format of finite element method

HE Zhaokui

（School of Science，Hohai University，Nanjing 211100，China）

Aiming at the problem that beginners reflect that the finite element method is difficult to program，based on the vector operation advantages of the software Python，the shape function vector and the shape function derivative vector are introduced，so that the calculation format of the finite element method is vectorized．The calculation format after vectorization is simple and easy to understand，easy to program，and easy to adjust according to the accuracy requirements and the transformation of boundary conditions.

finite element method；Gaussian integral；vectorization；program

1007-9831（2022）09-0062-05

O242.21∶G642.0

A

10.3969/j.issn.1007-9831.2022.09.013

2022-01-10

高等学校大学数学教学研究与发展中心项目（CMC20220203）；江苏省高等教育教改研究课题重点项目（2021JSJG090）；2021年江苏省高校“基础课程群”专项重点课题（2021JDKT017）；河海大学课程思政示范课程建设项目（2021A05）

何朝葵（1974-），男，湖南郴州人，讲师，硕士，从事有限元方法教学研究．E-mail：hzk@hhu.edu.cn