基于离散元EDEM的米粒破碎特性分析

刘 程 王旺平 宋少云

(武汉轻工大学机械工程学院，湖北 武汉 430024)

碾米机碾白过程中存在米粒与米粒、米粒与碾辊、米粒与米筛之间的碰撞，在碰撞过程中会产生碎米，米粒破碎率是评价碾米机碾白效果的重要指标之一。有关米粒破碎特性的研究已有大量报道，如周显青等[1]研究表明，糙米的品质对其力学特性及加工质量有较大的影响；吴中华等[2]研究了含水率和温度对糙米籽粒压缩破裂载荷的影响，结果表明破裂载荷随温度升高而下降，随含水率下降而增大，且含水率对破裂载荷的影响更为显著；李毅念等[3]分别以糙米的腹部、背部作为承压面，对糙米的3点弯曲破碎力学性能进行了测试，研究发现腹部的断裂能小于背部；冯帅博[4]利用自制撞击力试验平台对不同含水率、不同品种的糙米进行撞击试验，分析了糙米的撞击力学特性，最终得知糙米撞击动量与撞击力、含水率有关且影响糙米撞击力因子的主次顺序为撞击动量、含水率、品种；Mohapatra等[5]研究了3种籼稻的物理、化学和力学性能，并对糙米进行不同程度的碾磨，采用碾磨系数和磨损指数表示糙米品质。

此外也有学者对碾米加工时米粒破碎原因进行了研究，如：崔帆等[6]研究结果表明挤压破碎是碾白过程中糙米破碎的主要原因；张强等[7]利用离散元EDEM进行了碾白室运动过程的模拟并对米粒破碎原因进行了分析，结果表明米筛形状、碾筋个数及碾辊直径都对米粒破碎率有显著影响；贾富国等[8]对不同含水率的糙米进行碾米加工试验, 研究糙米的含水率对精米率、碾米加工的能耗、裂纹率及碎米率的影响规律。

上述研究大多是对糙米的力学特性进行的分析，以及结合米粒整机碾白表现对米粒破碎进行的分析，缺乏碾白过程中对米粒与各部件以及米粒与米粒间碰撞的深入研究。研究拟结合离散元法，利用EDEM软件对不同含水率、不同速度下的单粒米粒以及两粒米粒碰撞进行仿真，分析米粒碰撞时的碰撞破碎特性，以期为碾米机碾辊转速优化提供理论依据，减少碾白过程中米粒的碎米率。

1 米粒离散元接触力学模型

EDEM是一种离散元素法建模软件，可用于模拟和分析颗粒处理及生产操作过程，快速创建颗粒实体的参数化模型，EDEM软件已逐步应用于农业工程中，如谷物清选、干燥及输送等[9]。颗粒黏结模型(Bonded Particle Model)属于EDEM中一种基础模型，其原理是利用理想的弹性黏结键对基本粒子进行黏结，形成一个可破碎的聚合体。基本粒子间的黏结键可因拉伸、剪切、压缩等外部载荷的作用发生形变，从而达到模拟破碎的效果。

1.1 创建米粒离散元模型

依次选取含水率为10.6%，11.7%，13.9%，15.4%的糙米样品。建模时将米粒简化为椭球体，用长轴短轴的长度区分米粒的尺寸大小。然而现实中米粒的宽 (W) 与厚 (T) 并不相等，如图1所示。因此，设米粒长为L，短轴为宽(W) 与厚 (T) 之和的1/2，即 (W+T)/2。最终得到长轴为6.6 mm，短轴为2.2 mm的近似椭球体来模拟真实米粒[10]。

EDEM中米粒模型构建过程如图2所示：先用SolidWorks建立一个挤压填充模型[11]，向其中填充椭球体，再通过EDEM仿真挤压成型。填充椭球体的物理半径[12]0.22 mm，颗粒间接触半径0.264 mm(图3)。当黏结的颗粒距离小于0.264 mm时颗粒间就会形成黏结键。在几何体内部生成颗粒填充物后，将生成后的颗粒通过椭球几何体上半部挤压向下运动，得到如图2(b)所示完整椭球体。利用EDEM中 Hertz-Mindlin with bonding接触模型在椭球聚合体中的球颗粒间引入平行黏结键，即可形成用于模拟的可破碎米粒的椭球聚合体，如图2(c)所示。最终形成的带有黏结键的米粒模型(图4)。模型中颗粒颜色从蓝色到红色变化，代表键受力由小到大。图4为新建的米粒模型，此时颗粒受力最小，显示为蓝色。

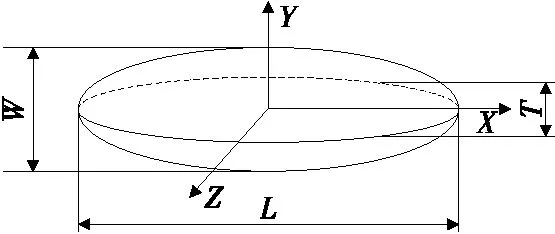
图1 米粒简化椭球体模型

图2 EDEM中米粒模型构建过程

图3 填充颗粒模型图

两粒米粒碰撞模型建立过程同上，只需增加一组挤压几何体模型，两组同时进行，如图5所示。

图4 椭球聚合体离散元模型

1.2 离散元仿真参数标定

当利用EDEM中Hertz-Mindlin with bonding接触模型对不同含水率的单粒米冲击破碎过程进行模拟时，还需确定除基本颗粒物性参数(泊松比、剪切模量和密度)和接触参数(恢复系数、静摩擦系数和滚动摩擦系数)以外的黏结参数，包括弹性黏结键单位面积法向和切向刚度、临界法向和切向应力以及黏结键截面半径等。目前黏结参数通过单轴压缩、三轴压缩、巴西盘劈裂等常规力学试验获取。所建模型的黏结参数以及球颗粒间静摩擦系数见表1[12]。

图5 两粒米粒离散元接触模型

表1 弹性黏结键参数

2 米粒碰撞仿真过程与结果

2.1 单粒米粒碰撞仿真

对相同含水率的单粒米粒设定不同的碰撞速度进行

碰撞仿真，碰撞结果见表2，仿真中出现的4种米粒碰撞状态分别为米粒完整、米粒基本完整、米粒轻微断裂、米粒断裂。由表2可知，当含水率固定时，米粒破碎率随米粒碰撞速度的增加而升高；黏结键断裂个数也随之增加，米粒状态也发生了变化。当速度为15.0～22 m/s时，米粒完整且无连接键被破坏,模型见图6；当速度为22.5～23.5 m/s时，米粒轻微碎裂，部分连接键被破坏，填充颗粒部分脱落，模型见图7；当速度为 24.0～27.5 m/s时，米粒断裂，中间连接键断裂，模型见图8。因此，米粒破碎状态可分为完整米粒、轻微破碎米粒、断裂米粒3种状态。

图6 单粒米粒碰撞后完整米粒模型图

图7 单粒米粒碰撞后轻微破碎米粒模型图

表2 不同含水率单粒米粒在不同速度下的碰撞结果

图8 单粒米粒碰撞后断裂米粒模型图

根据米粒破碎状态可反向推导出不同含水率的单粒米粒临界破碎速度。由图9可知，米粒破碎临界速度随含水率增加而降低。含水率10.6%的完整米粒能承受的最大临界破碎速度为23.5 m/s，含水率13.9%的轻微破碎米粒能承受的最大临界破碎速度为27.5 m/s。因此，不同含水率对米粒破碎速度有着直接影响且存在一个最优含水率对米粒破碎影响最小。

图9 单粒米粒在不同含水率下临界破碎速度

2.2 两粒米粒碰撞仿真

对相同含水率的两粒米粒设定不同的碰撞速度然后进行碰撞仿真，碰撞结果见表3，仿真中出现的4种米粒碰撞状态分别为① 两粒米粒完整；② 米粒基本完整，下方米粒下部轻微破碎；③ 米粒基本完整，下方米粒上下部位皆轻微破碎；④ 下端米粒断裂。由表3可知，含水率固定时，米粒破碎率随米粒碰撞速度的增加而升高，黏结键断裂个数也随之增加，米粒状态也发生了变化。

表3 不同含水率两粒米粒在不同速度下的碰撞结果†

当速度为13.0～22.0 m/s时，两粒米粒完整且无黏结键被破坏，模型见图10；当速度为21～28 m/s时，米粒基本完整，下方米粒和碰撞台接触部位轻微破碎，15个黏结键被破坏，模型见图11；当速度为29～43 m/s时，米粒基本完整，下方米粒上下部位皆轻微破碎，60～77个黏结键被破坏，模型见图12；当速度达到44 m/s时，米粒断裂，中间黏结键断裂，模型见图13。因此，米粒状态可分为米粒完整、底部米粒下方轻微破碎或上下方皆轻微破碎、底部米粒断裂3种临界破碎形态。

图10 两粒米粒碰撞后完整米粒模型图

图11 两粒米粒碰撞后轻微破碎米粒模型图

图12 两粒米粒碰撞后上下部位少量破碎米粒模型图

图13 两粒米粒碰撞后断裂米粒模型图

根据米粒破碎状态可反向推导出不同含水率的两粒米粒临界破碎速度。由图14可知，两粒米粒与单粒米粒碰撞相似，也存在一个最优含水率，使米粒完整和不断裂时能承受较大的速度。两粒米粒碰撞下，米粒完整和不断裂时的最优含水率皆为10.6%，其速度分别为22，46 m/s。

综上，含水率10.6%的单粒米粒碰撞或两粒米粒碰撞破碎速度相似。米粒完整时，单粒米粒和两粒米粒皆在含水率10.6%时临界破碎速度最大，碰撞效果最优，临界速度分别为23.5，22.0 m/s。含水率对米粒破碎具有较大影响，且在设定的范围内，含水率越高，米粒越容易破碎。

图14 两粒米粒在不同含水率下的临界速度

3 结论

运用SolidWorks建立米粒挤压模型，以含水率、碰撞速度为变量，利用EDEM中颗粒黏结模型对单粒米粒和两粒米粒进行碰撞仿真，结果表明单粒米粒碰撞断裂速度远小于两粒米粒碰撞断裂速度，不同速度对米粒破碎有着显著影响；不同含水率的米粒临界破碎速度不同，含水率对米粒破碎率影响显著，含水率越高，米粒越容易破碎。综上，存在一个最优含水率对米粒破碎率影响最小。但含水率设定相对较少，且梯度相对较大，后续需对更多不同含水率的米粒黏结键参数进行测定，寻找最优含水率和米粒不破碎所能承受的最大碰撞速度，从而对碾米机碾辊速度进一步优化，减少碾白过程中米粒的碎米率。