高效液相色谱法测定中果酒中山梨酸含量的不确定度评定

在防腐保鲜剂中，山梨酸具有高效性和安全性，这是得到国际社会共同认可的[1]。其作用机理是通过降低食品中微生物脱氢酶的活性抑制微生物的生长和繁殖，广泛应用于多种行业[2]。因此，对食品中的山梨酸的定性和定量检测在保障食品安全方面至关重要[3-5]。本研究采用GB 5009.28—2016方法测定果酒中山梨酸的含量，并依据JJF 1059.1—2012对实验过程中各分量所产生的不确定度进行评估计算。

1 材料与方法

1.1 材料与试剂

果酒来自食品安全监督随机抽样样本；乙酸铵：致远化学试剂有限公司（天津）；甲醇：Merck公司（德国）；水中山梨酸（1.00 mg·mL-1）：北京坛墨质检科技有限公司。

1.2 仪器与设备

LC-2030C 3D高效液相色谱仪：日本岛津；MS205DU电子天平：瑞士Mettler-Toledo。

1.3 方法

1.3.1 样品前处理

准确称取约2 g果酒于50 mL容量瓶中，用纯化水定容至刻度，混匀，取上清液经0.45 μm滤膜过滤，按照液相色谱仪操作进样测定。

标准溶液配制：准确量取山梨酸标准品5.0 mL于10 mL容量瓶，用水定容至刻度得到500 μg·mL-1的中间储备液。精密吸取山梨酸中间溶液0.10 mL、0.20 mL、0.40 mL、0.80 mL和1.00 mL于10 mL容量瓶，用超纯水定容至刻度，配制成质量浓度分别为5 μg·mL-1、10 μg·mL-1、20 μg·mL-1、40 μg·mL-1和 50 μg·mL-1的标准曲线溶液。

果酒中山梨酸含量测定：样液由液相色谱仪进行峰面积测定，根据标准工作曲线计算得到果酒中山梨酸的质量浓度。

1.3.2 建立数学模型

按照以上试验操作，建立果酒中山梨酸的含量不确定度数学模型为

式中：X为果酒中山梨酸含量，g·kg-1；C为由标准曲线计算出果酒待测样液的浓度，μg·mL-1；V为稀释后的试样体积；m为果酒质量，g；1 000为单位换算因子。

2 结果与分析

2.1 确定不确定度的来源

从样品前处理、液相色谱测定以及数学模型可知，测定果酒中山梨酸含量不确定度主要来源于标准溶液引入urel(std)、校准曲线建立引入urel(S)、实验前处理引入urel(P)和样品重复性测量引入urel(R)。

2.2 不确定度分量因素的量化计算

2.2.1 标准物质引入的不确定度urel(std)

本实验采用的标准品为水中山梨酸，浓度为1.00 mg·mL-1，扩展不确定度为±1%（k=2）。则山梨酸标准品引入的不确定度为

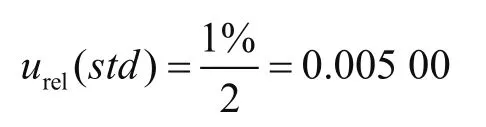
2.2.2 配制标准溶液和建立校正曲线引入的相对不确定度urel(S)

（1）由配制标准中间工作液引入的不确定度urel(S1)。①5 mL刻度吸管引入的相对不确定度urel(S1-1)。规定5 mL刻度吸管（A级）容量允差为±0.025 mL，采用B类评定方法，取矩形分布，则

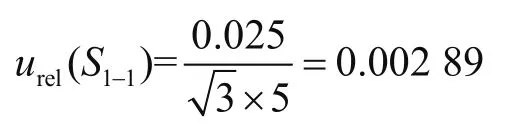
②定容至10 mL容量瓶引入的相对不确定度urel(S1-2)。则

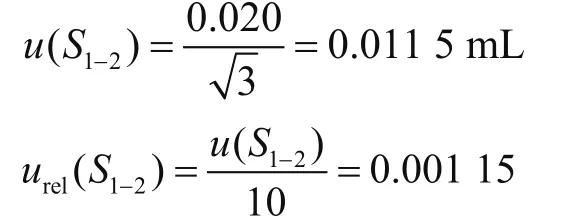
③温度变化引入的相对不确定度urel(S1-3)。实验室温度控制在20 ℃±5 ℃，此温度下玻璃膨胀系数为2.5×10-5/℃，水的体积膨胀系数为2.1×10-4/℃。取均匀分布计算

合并以上分量相对不确定度，则由配制中间标准溶液过程引入的相对标准不确定度为

（2）标准中间工作溶液稀释成系列标准工作曲线引入的不确定度urel(S2)。吸取标准中间工作溶液0.10 mL、0.20 mL、0.40 mL、0.80 mL和1.00 mL于10 mL容量瓶中，引入的不确定度如下。配制标准曲线使用了0.1 mL、0.2 mL、0.5 mL、1.0 mL刻度吸管，依照相关规程JJG 196—2006、JJG 646—2006规定，按均匀分布并取矩形分布，采取B类评定方法，则由刻度吸管引入的相对标准不确定度urel(S2-1)为

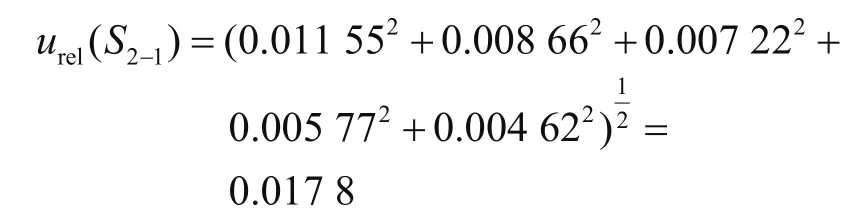
吸取的标准中间工作液定容于10 mL容量瓶，引入的不确定度主要是容量瓶定容引入u(S2-2)和温度变化引入u(S2-3)。依照相关规程JJG 646—2006和JJG 196—2006的规定，10 mL容量瓶最大允差±0.020 mL，按照B类评定方法，取矩形分布，则按照均匀分布计算，则

合并以上分量相对不确定度，则由标准中间溶液配制成标准工作曲线引入的相对不确定度为

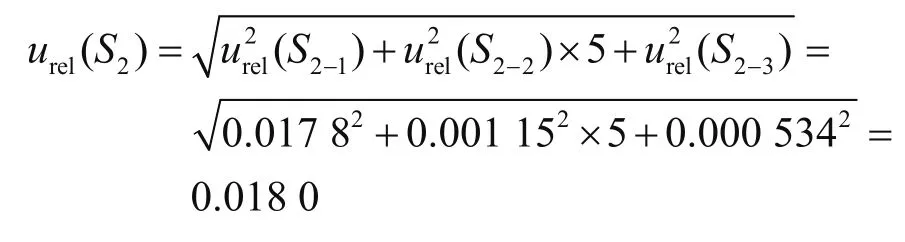
（3）建立校准曲线引入的不确定度urel(S3)。5个不同浓度标准工作溶液对应的峰面积见表1，结合校准曲线为y=a+bx和最小二乘法拟合，得出a=-1 599.87，b=60 292.79，在下列各式中视为常数。

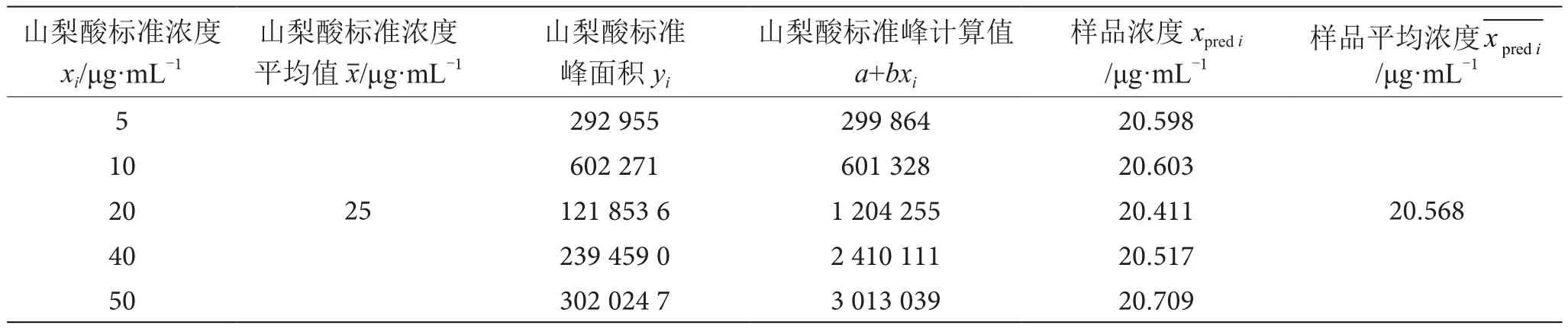
表1 标准工作液与样品测得结果表

根据公式（2）、（3）计算校准曲线引入的不确定度urel(S3)为

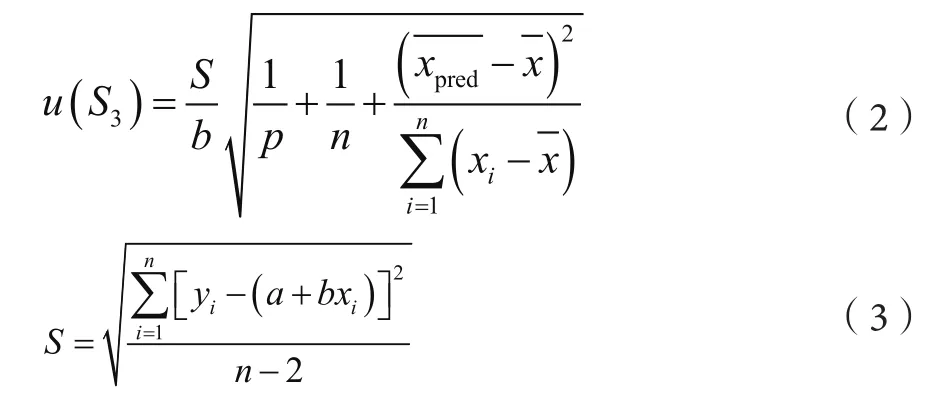
式中：xpredi为测定山梨酸含量引入的不确定度；S为由拟合直线求得与相应yi测定值之差按贝塞尔公式求出的残余标准误差；p为样品溶液测定次数；n为标准溶液测定次数；为山梨酸浓度平均值，μg·mL-1；为山梨酸标准溶液浓度平均值，μg·mL-1。

将表1中各数据代入公式（2）、（3），计算得S=13 483.51，u(S3)=0.144 μg·mL-1，则校准曲线引入的不确定度为

合并以上分量，由建立标准曲线引入的不确定度为

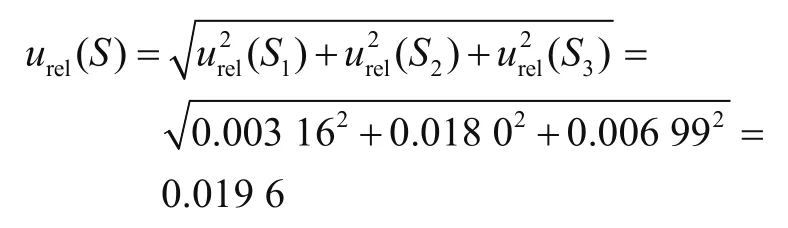
2.2.3 试样前处理引入的不确定度urel(P)

（1）试样称样引入的不确定度urel(P1)。称量样品使用的天平（MS205DU），不确定度为U=0.02 mg，k=2，由此引入的不确定度为u(P1)=0.000 02/2=1.000×10-5g；由称取果酒样品为2.000 g引入的相对标准不确定度为urel(P1)=u(P1)/2.000=5×10-6。

（2）由定容体积引入的不确定度urel(P2)。样品处理后用50 mL的A级容量瓶定容，参照《常用玻璃量具检定规程》，其最大允许误±0.05 mL，采用B类评定方式，考虑由矩形分布引入的不确定度为则定容的相对标准不确定度为urel(P2)=u(P2)/50=5.78×10-4。

（3）温度变化引入的样品定容不确定度urel(P3)。根据均匀分布则50 mL容量瓶的温度波动引入的标准不确定度为u(P3)=50×(2.1×10-4-2.5×10-5)×则相对标准不确定度为urel(P3)=u(P3)/50=5.34×10-4。

合并以上分量，由试样前处理引入的不确定度为

2.2.4 试样测定结果重复性的不确定度urel(R)

本实验考察了仪器测试稳定性，对同一样品重复测量5次，所得结果分别为 0.515 0 g·kg-1、0.515 0 g·kg-1、0.510 3 g·kg-1、0.512 9 g·kg-1和 0.517 7 g·kg-1。采用 A类评定，应用贝塞尔法计算，则重复测量同一样品量引入的标准不确定度为

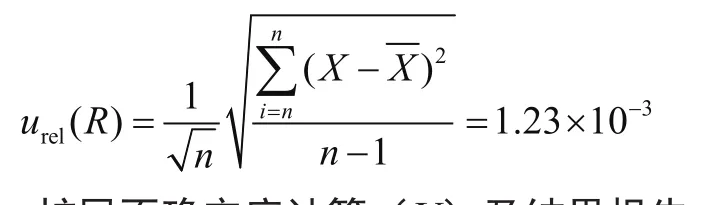
2.3 扩展不确定度计算（U）及结果报告

综合以上结果，根据影响本测定实验不确定度urel(std)、urel(S)、urel(P)、urel(R)的各分量合成计算，得出果酒中山梨酸含量测定的相对不确定度urel(T)为

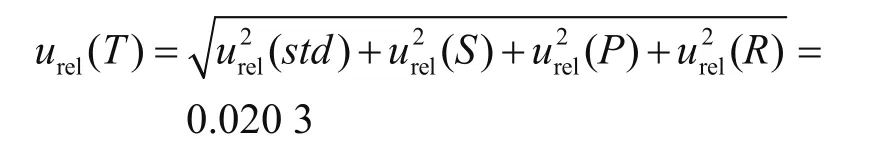
试样中山梨酸含量的算术平均值为0.514 0 g·kg-1，则标准不确定度为urel(t)=urel(T)×0.514 0=0.010 4 g·kg-1。

取包含因子k=2得出扩展不确定度为

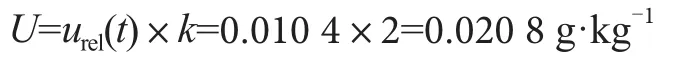
因此，在置信概率P=95%（k=2）时，本实验果酒中山梨酸含量的测定不确定报告为X=(0.514 0±0.020 8) g·kg-1，k=2。

3 结论

本研究对高效液相色谱法测定果酒中山梨酸所引入的不确定度各分量进行分析和合成，结论得出配制标准工作溶液引入的不确定度贡献率最大（87.7%）。针对以上数据，为有效提高测定结果的准确性，关键控制点在于减少建立校正曲线时配制系列工作曲线引入的误差，所以需要减少小体积的移取偏差，可以通过将刻度吸管换为更精准的进口移液器，减小允差，同时使用高精度的量具来减小引入的不确定度，定期维护和检定移液枪和量具。此数学模型可为其他液相色谱测定酒类添加剂不确定度研究提供参考。