光伏电池输出特性及MPPT仿真

朱煜伟，刘梁挺

（安徽理工大学 电气与信息工程学院，安徽淮南， 232001）

能源贯穿了人类发展的历史，化石能源仍旧是现在世界各国消耗的主要能源。由于化石能源的产出不可持续，短时间内并不能再生。人类文明进入工业化以来，能源的需求量与日俱增，而由于人类的工业活动导致的全球气候变暖的问题已经迫在眉睫，气候变化已成为当今人类社会面临的重大全球性挑战。对此，我国承诺在2030年实现“碳达峰”，并在往后逐渐减少碳排放，并在2060年前实现“碳中和”，实现“碳达峰”、“碳中和”也是当前全球竞争的核心所在，这将引领各国新一代技术的研发，未来一段时间全球将进入一个能源、工业、交通等领域技术变革的时代[1]。

1 光伏电池工作原理

光伏电池依据PN结光生伏特效应原理，是通过光能照射到半导体材料上来产生电能的。光生伏特效应的原理在于光照并非均匀，即物体的各个部位受光照的强度并不相同，当太阳光照射到PN型半导体材料上时，由光的能量所产生的光子将半导体材料中不稳定原子周围的核外电子从原子核的束缚中挣脱，形成自由电子，就在PN结上生成了电子-空穴对，电子和空穴成对出现，在很短时间又结合在一起，即电子的复合。由于P型和N型的半导体化学特性上的差异，当它们被结合在一起时会在它们的结合面上产生PN结，其中P型半导体一侧带负电，而N型一侧带正电，由此就会出现浓度差，浓度差会使N区多余的自由电子扩散至P区，P区空穴移动到N区，当浓度达到平衡时，电子将不再扩散，从而形成了电荷通道，方向是由N区指向P区，形成电势差，从而产生电流的流动[2]。所以在等效电路中，就可以把光伏电池看作是一个恒流源。

2 光伏电池数学模型分析

光伏电池等效电路的推导公式如下：

式中Rsh为等效并联电阻，Rw为等效串联电阻，由于光伏电池的漏抗Rsh数值很大，又有Rw远远小于二极管导通时的阻值，所以理论上这俩阻抗可以忽略，整理上述内容和公式的输出电流与电压的简化关系式：

其中，Iph为模拟光伏电池光电效应产生的电流；ID0为反向饱和电流；q=1.6×10-19C，即单位电子电荷量；n为二极管因子；K是玻尔兹曼常数，为1.38×10-23J/K；T是绝对温度。光伏电池的等效电路，如图1所示。图中二极管表示电池内部等效的PN结。

图1 光伏电池等效电路图

影响光伏输出特性的因素分别是外界温度T和光照强度S。规定标准环境下的数值Isc、Im、Um、Uoc，通过改变外界条件[3]，得到响应状态数值，加入修正补偿系数后联立公式可以得出光伏电池的输出特性曲线，公式推导过程如下：

上述公式中T和S是实验温度和实验光强，ΔT和ΔS分别为实验温度与规定标准温度的差值，以及实验光强和规定标准光强的差值，Im’、Isc’、Um’、Uoc’分别为其对应参数的修正值，Sref=1000W/m2，Tref=25℃，a=0.0025/℃，b=0.5，c=0.003/℃，e为自然对数[4]。

3 光伏电池输出特性仿真分析

设定标准环境下Im=8.10A，Isc=9.20A，Um=30.60V，Uoc=36.50V，根据上述公式和参数在Matlab/Simulink中搭建仿真模型。如图2所示。

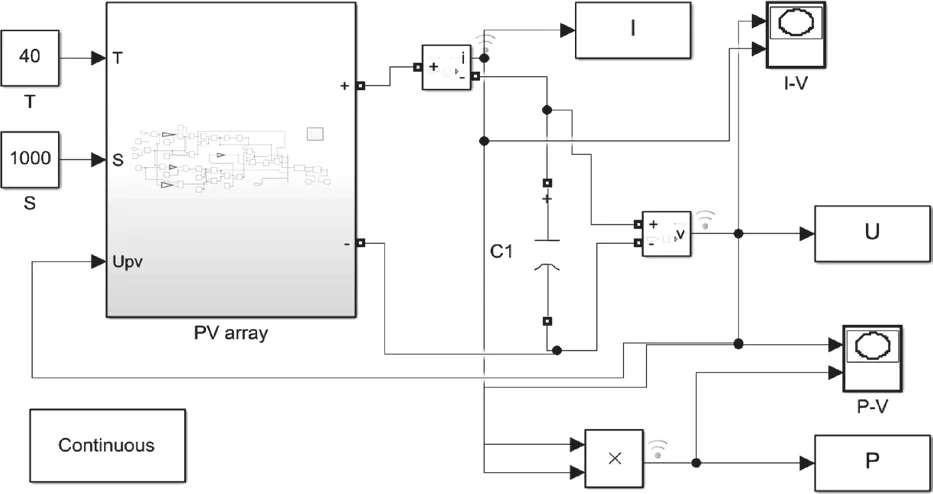
图2 光伏电池仿真模型图

运用搭建的仿真模型，设置外界环境参数在光照1000W/m2，温度25℃的标准环境下，可以得到如图2的输出特性曲线。

图3中实曲线为P-U特性曲线，虚曲线为I-U特性曲线，从I-U特性曲线中可以看出光伏电池在输出较低电压时呈现近似恒流源的特性，而在输出较高电压时又会呈现恒压源的特性。从P-U特性曲线中可以看出光伏电池在光照和温度固定的前提条件下，有且只有一个最大功率点。

图3 标准状态下光伏输出特征曲线

运用所搭建的仿真模型分析在不同光照下的光伏电池输出特性，即保持温度这一参数固定在25℃，探究改变光照强度对于光伏电池输出特性的影响，其输出特性分为P-U输出特性和I-U输出特性，如图4所示。实线光强为1000W/m2，虚线光强为800W/m2，点虚线光强为600W/m2。

从图4中可以得到光伏电池在光照强度逐步提升的状态下，输出特性曲线也随之上升的结论，上升幅度十分明显，体现光伏电池输出功率与光强之间的正向相关关系。

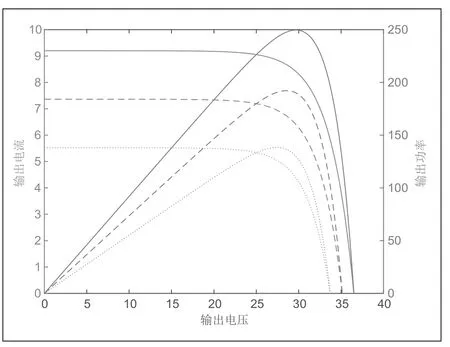
图4 不同光照下光伏电池输出特性曲线

接着在光照强度固定在1000W/m2的条件下，模拟温度对光伏电池的影响，输出特性曲线见图5。其中实线温度为40℃，虚线温度为25℃，点虚线温度为10℃。

从图5中可以看出，当光照强度固定不变时，光伏电池的开路电压随温度上升而减小，短路电流稍有增大；最大功率点随温度的增加而小幅减小，同时在最大功率点处的电压也逐步变小。输出特性曲线随温度的变化而变化的幅度不大，温度与光伏电池输出之间的关系没有光照那么明显。

图5 不同温度下光伏电池输出特性曲线

从以上仿真结果得知，光伏电池属于一种非线性电源，其输出特性也同环境温度以及光照强度的变动密切相关，在环境温度或者光照强度一定时，光伏电池只存在一个最大功率点。光照强度的改变对光伏电池输出功率的影响远较环境温度改变的影响大。

4 光伏MPPT仿真分析

由上述仿真结果可以得知光伏电池的输出特性曲线是非线性的，且与工作的光照强度、环境温度密切相关。可以知道随着光照强度和温度变化的影响，电池并不是时刻都工作在最大功率点的。为了得到光伏电池的最大功率点的输出，需要进行最大功率点的跟踪研究，即MPPT控制技术，使电池能随时处在最大功率点进行工作。现今实际工程应用中常见的基于扰动的自寻优最大功率跟踪算法有扰动观察法、电导增量法、波动相关控制法等[5]。

其中电导增量法（INC）是从光伏电池输出功率随输出电压变化而变化的规律入手，整理总结光伏电池工作于最大功率点时的电导和电导变化率之间的对应关系，推导出的一种MPPT控制方法。INC通过设定一个变化量，来判断当前光伏电池工作在最大功率点的哪一侧。在最大功率点右侧时，变化量为负；在最大功率点左侧时，变化量为正。并且从一个稳态过渡到另一个稳态时，根据输出电流的变化就能做出正确判断，最终稳定在最大功率点的附近。其控制流程图见图6。

图6 电导增量法流程图

在两级式光伏逆变系统中，MPPT通常通过Boost电路来实现，Boost电路是一种升压式斩波电路，在光伏系统中起着将光伏电池输出的不稳定直流电能转化为稳定的直流电能的作用。其基本工作电路由输入电容、电感、开关管、二极管和输出电容共同组成。电路拓扑图见图7。

图7 Boost电路拓扑图

对照拓扑图，下面简要分析一些其工作原理。开关管S在一个开关周期T内有两种开关状态，Boost电路对应就会有两种工作状态。当开关管S导通时，导通时间Ton内输入电压Uin向电感L充电，电容C2给负载供电。当开关管S关断，关断时间Toff内，电感L和电源同时为C2充电并供能给负载。由于一个开关周期内只有导通和关断两种状态，所以占空比D为Ton与T的比值[6]。电感L是储能元件，根据其原理可知L吸收与释放的能量是守恒的，综合其工作原理，我们可以得到Boost电路输出电压与输入电压的比值为1/1-D，由此可以得到控制占空比即可控制输出电压这一结论。而实际上MPPT正是通过控制占空比D来进行最大功率点追踪的。

根据INC的控制原理，在算法中需要求电压和电流的微分，而在实际控制中，常使用瞬时增量来代替微分进行控制，达到简化算法的目的。已知有P=UI，两边同时对U求导后替换微分量并对式进行变换，可得工作点判断式I/U+ΔI/ΔU，当判断式等于0时，工作点位于最大功率点上，MPPT不改变占空比，电压不变；当判断式小于0时，工作点位于最大功率右侧，MPPT增大占空比，电压减小；当判断式大于0时，工作点位于最大功率点左侧，MPPT减小占空比，电压增大[7]。

根据MPPT控制的原理，使用本文中的仿真电源，Boost电路参数如下：输入滤波电容C1=0.0001F，输出滤波电容C2=0.0024F，电感L=0.005H，开关频率fk=10kHz。搭建仿真模型图8。

图8 MPPT-INC仿真模型图

仿真温度设置为25℃，初始光照强度为1000W/m2，到第3秒时下降到800W/m2而后又在第6秒上升到1200W/m2。在此条件下对INC进行仿真，仿真结果见图9。

图9 INC功率输出曲线

从仿真结果图可知，INC能很好地踪到最大功率点，即使外界环境如光照强度改变，也能很快的在此追踪到最大功率点。然而，从图上还能看出实际上光伏电池的工作点其实一直在最大功率点附近震荡，这是传统INC无法避免的。所以在那些精度要求较高的工程中，常常将智能算法与传统MPPT相结合的方式来进行最大功率点跟踪控制。

5 结论

本文中选择了一个适用于实际工程设计的简单光伏电池数学模型，并在Matlab/Simulink的环境中建立仿真模型，并进行了传统INC的控制仿真。仿真结果显示，该模式是合理的、可行的，并且能够精确反映环境条件和光照强度变化以及时光伏电池的输出特性，为进一步MPPT以及光伏发电系统的研究，创造了良好的模拟电源。