基于CHES-FY系统的织物触感风格等级评价

2022-10-19杜赵群

丝绸 2022年10期

阳丹, 杜赵群, 刘贵, 林旭

(1.东华大学纺织面料技术教育部重点实验室,上海 201620; 2.福建省纤维检验中心福建省纺织产品检测技术重点实验室,福州 350026)

织物风格特征是人对织物的物理力学性能和形态特征所做出的反应,织物的风格特征主要取决于织物的弯曲性能、剪切性能、压缩性能、拉伸性能及表面摩擦性能等物理力学性能[1-2]。最早Peirce的悬臂梁弯曲模型通过定量测试织物的弯曲性能,客观表征织物的硬挺度,并提出织物触感风格主要由弯曲刚度、压缩性能和表面摩擦力三个因素决定[3]。目前国内外较为通用的风格仪分别是KES[4]系统和FAST[5]系统,其中KES系统使用多元回归的方法客观表达织物风格的物理力学量,但物理力学量之间的相关性没有被考虑,具有一定的数理统计缺陷[6]。FAST系统通过指纹图对面料性能和用途进行快速分析,但没有考虑织物的手感弹性检测[7]。近年PhabrOmeter风格评价系统在国内企业和高校广泛研究[8-9],该系统主要是基于环形测试的测量模式,利用加权欧式距离计算织物对应的综合触感值。有学者研究了丰宝仪测试指标的物理意义,发现其测试结果与常用仪器测试结果相关性较弱,并且与主观试验结果存在较多不符的情况,认为其存在指标表征能力较弱等缺陷[10]。CHES-FY风格仪[11-14]基于三点梁弯曲原理,通过一次测量便可得到表征织物柔软度、硬挺度、滑爽度及松紧度风格特征值,CHES-FY系统具有测试效率高和成本低等特点,并且广泛应用于服装质量检测和面料设计过程中对面料性能的预测。但目前CHES-FY风格仪还缺乏客观的等级评价系统,将主观评级与客观测试结果进行线性回归分析得到织物风格评价模型[15-16],在主观评级过程中存在一定的人为主观性。杜赵群等[17]使用动态模糊聚类与加权欧式距离度量准则,对服装面料风格进行聚类分析,实现了织物的分类,但没有对织物各基本风格指标值进行等级评价。Shao Y等[18]将Ward层次聚类与K-means聚类算法结合分析,对织物接触压迫舒适进行聚类讨论,通过绘制谱系图虽可以观察到数据的分类特征,但其最终的簇类数目还是由主观观察数据分布得到。

针对目前CHES-FY风格仪缺乏客观等级评价系统,使用主观评级或者在K均值聚类中以经验判定K值的方法存在主观因素影响,因此本文使用CHES-FY风格仪测试织物触感风格,结合簇内误差法和轮廓系数法客观选取K值,运用K-means聚类统计分析方法,对四项基本风格指标的等级进行划分,进一步利用贝叶斯判别法建立了判断织物基本风格等级模型,为形成科学客观的织物风格等级评价系统提供理论依据,实现对织物风格等级作出快速客观评价。

1 试验

1.1 试验样品

选取60块在材质、颜色、厚度及平方米质量等方面上差异较大的织物,试样材质成分包含了棉、涤纶、羊毛、蚕丝、粘胶、氨纶及尼龙等常用纤维,其中35块试样为机织物,25块试样为针织物,试样实物图如表1所示。距布边边缘至少150 mm裁剪试样,在经向、纬向和45°方向各裁剪3块,试样裁剪尺寸为500 mm×55 mm,并用于CHES-FY系统测试织物触感风格;另外裁出5块10 cm×10 cm的方块,用于YG141N测厚仪测量织物厚度,测得60块织物的厚度在0.055～7.577 mm;并用电子天平称量其质量,测试后转化成平方米质量,测得平方米质量在25～475 g/m2。上述所有试验均在标准大气温湿度(20±2) ℃、湿度(65±3)%条件下进行,并且测试前试样均在标准大气温湿度下进行调湿处理24 h。

表1 试样实物Tab.1 Sample physical drawing

1.2 CHES-FY风格仪

CHES-FY风格仪是由东华大学与南通宏大实验仪器有限公司联合研发,属于单台单测多指标式风格仪,如图1(a)所示。该系统是基于三点梁弯曲原理,通过在测试过程中抽拔试样,使试样与三点梁机构交互作用,在不同阶段构造其形变,形象地模拟人手对面料主观感受的过程。根据各变形采集的力—位移曲线提取定量化指标,得到柔软度指数、硬挺度指数、滑爽度指数和松紧度指数指标,进而表征纺织材料触感风格相关的物理力学性质。三点梁是指测试设备的主要测试部件是一个三点梁结构,上面一个压杆,下面两个支撑杆,织物在上下三根杆中间实现小应力下的应变,如图1(b)所示。

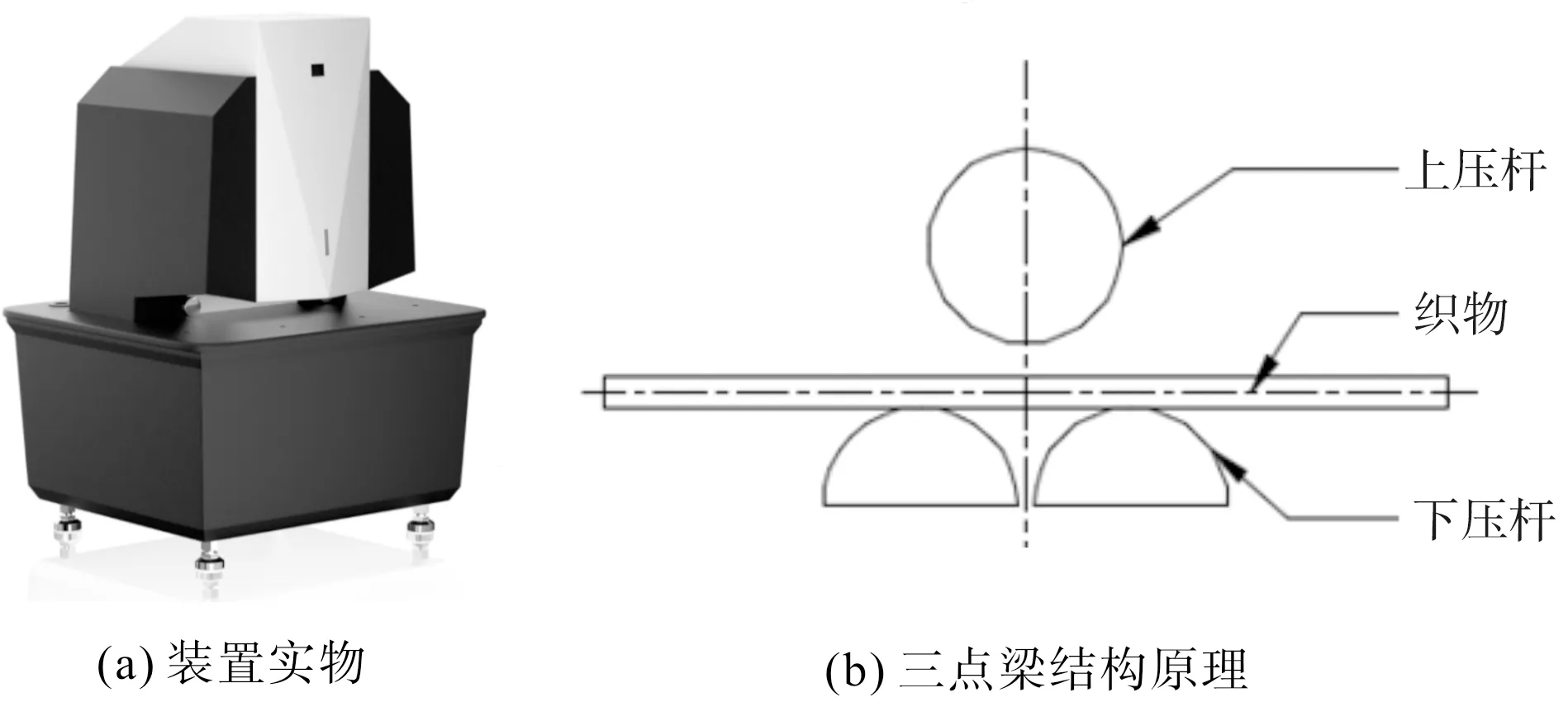
图1 CHES-FY风格仪装置及原理Fig.1 Device and schematic diagram of CHES-FY style instrument

1.3 曲线与测试指标

使用CHES-FY风格仪对面料进行测试,以52#试样为例,所得典型力—位移曲线如图2(a)所示。测试曲线包含压缩、弯曲、摩擦和拉伸四个阶段,设备测试过程示意如图2(b)所示。根据各阶段的力—位移曲线提取表达织物基本风格特征指标值,指标含义及表征方法如表2所示。

图2 CHES-FY风格测试曲线及过程Fig.2 Test curve and process of CHES-FY style

表2 CHES-FY风格仪指标含义及表征Tab.2 Meaning and characterization of CHES-FY style instrument indicators

系统参数设置如下:测试过程中压杆速度为24 mm/min;压缩阶段定压力值为200 cN;弯曲阶段弯曲挠度值为20 mm;摩擦阶段的定压力值为50 cN;拉伸阶段的定压力值为400 cN,在实际测试中,由于位移控制器本身有量程限制,所以对于拉伸阶段,结束情况分为两种,一是达到拉力值400 cN,另一个是达到位移控制器有效限制量程结束。

60块织物测试结果统计如表3所示,其中16#织物为涂层覆膜织物,将试样裁剪成500 mm×55 mm的长条形状时,该试样在无外力作用时织物易发生起翘,无法平整放于试验台上,因此在压缩和弯曲过程测试异常,其柔软度和硬挺度数据舍弃,摩擦和拉伸受外力作用后正常测试,其滑爽度和松紧度结果保留。从统计结果可以看出,所选试样织物风格指标具有较大差异性,适合织物风格的聚类研究。

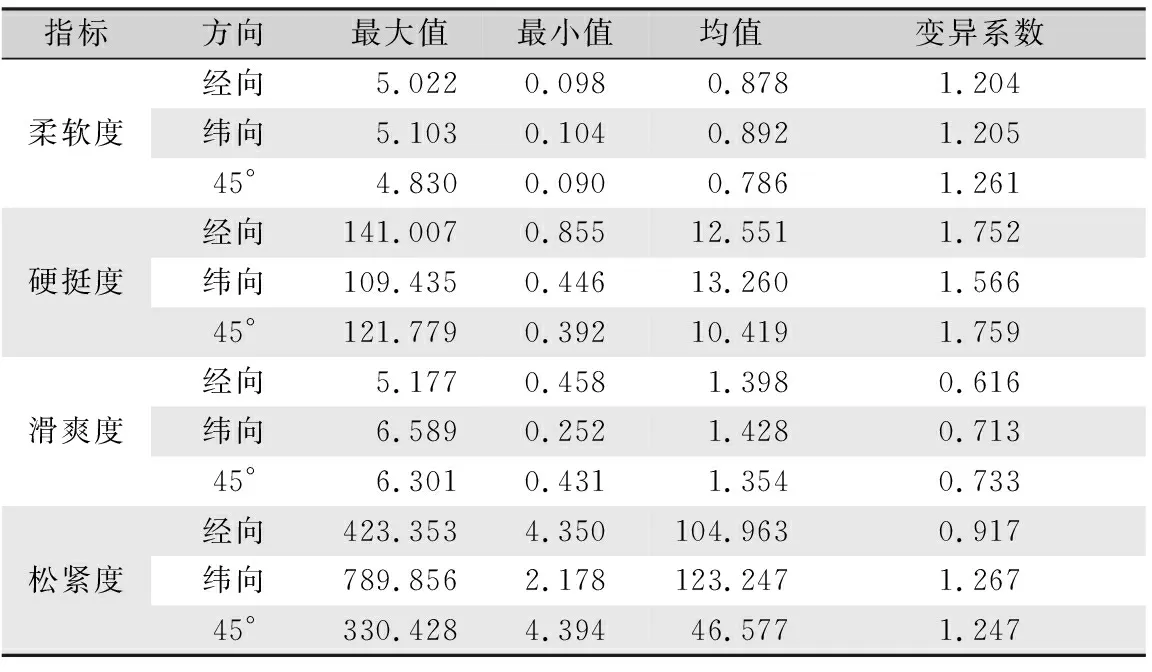
表3 CHES-FY风格仪测试结果统计Tab.3 Statistics of test results of CHES-FY style instrument

2 结果与分析

在无监督学习中,对于没有分类标签的数据集,聚类分析可通过学习样本数据本身的内在规律得到聚类结果。对于有限数量样本的聚类,K-means聚类算法是一种简单快速的聚类分析方法,其先根据样本量值确定初始聚类中心,再计算每个样本量与初始聚类中心之间的欧拉距离Dit,计算公式如下(其中i=1,2,…,m;t=1,2,…,K),并根据欧拉距离将样本分在距离最小的类中,若聚类中心发生变动则重新计算各类质心。

(1)

但是K-means聚类算法需要对K值大小进行选择,以经验判定K值的方法存在人为主观性,K值的选定是决定聚类效果好坏的重要因素之一,所以客观选择合适的K值十分重要。因此本文使用K-means聚类算法,结合簇内误差平方和和轮廓系数法,优选合适的簇内数目K值,分别对织物各单项基本风格测试结果进行分类。

2.1 K值的选取

2.1.1 簇内误差平方和

为了确定K-means聚类算法的K值,使用簇内误差平方和(Sum of squared errors,SSE)用来评价聚类函数效果的目标函数,算法目的是寻找使SSE最小化的结果,可以通过作图的方法,观察K值与SSE折线图,当SSE折线出现坡度骤减时,则表示增加了一个比之前方案更多的类别,将带来更好的收益;反之,则可能强加了一个超出需求的类别。因此,选择折线坡度骤减的点作为最优K。设定含有n个数据对象数据集合X={x1,x2,x3,…,xn},由K-means算法进行聚类后产生的类别集合为C={C1,C2,C3,…,Ck},则算法目标函数SSE的定义如下:

(2)

式中:Ck是簇Ck的中心点。

计算方法如下:

(3)

2.1.2 轮廓系数法

簇内的稠密程度(簇内差异小)和簇间的离散程度(簇外差异大)用来评估聚类效果的好坏,其中轮廓系数(Silhouette coefficient,SC)是常用于度量聚类效果好坏的指标,SC越接近于1表示聚类效果越好,计算所有样本的SC均值作为聚类结果的轮廓系数,单个样本SC计算方法如下。

(4)

式中:a(i)表示样本i到与样本i属于同类别的其他样本之间的平均距离,b(i)表示样本i到与样本i不属于同类别的其他所有样本之间的平均距离。

2.1.3 优选K值

结合簇内误差平方和法和轮廓系数法,使用聚类内部的inertia变量绘制K-SSE折线图,并且使用silhouette_score函数计算K值对应轮廓系数,绘制K值与silhouette_score折线图。由图3和图4可以观察到,对于柔软度K=5为K-SSE折线拐点处,并且轮廓系数最大,因此柔软度选取K=5;对于硬挺度K-SSE折线未出现较为明显的拐点,但轮廓系数K=3时最大,因此硬挺度K值选取3类;滑爽度在K=4时曲线开始平缓下降,并且轮廓系数相对较大,因此滑爽度选取4个类别;松紧度K-SSE折线未有较未明显拐点,结合轮廓系数K=5时,轮廓系数最大,因此选取K=5作为类别数。

图3 K值与SSE折线图Fig.3 Line chart of K value and SSE

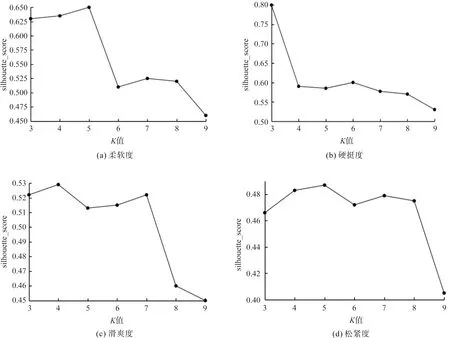
图4 K值与轮廓系数折线图Fig.4 Line chart of K value and silhouette coefficient

2.2 K-means聚类结果及分析

根据各风格指标优选的K值,对CHES-FY系统测得风格指标结果进行聚类,得到样本的聚类结果,如图5所示。柔软度类别数越高表示织物越柔软,1级表示不柔软,2级表示相对不柔软,3级表示一般柔软,4级表示相对柔软,5级表示柔软。硬挺度类别数越低表示织物越硬挺,1级表示织物硬挺,2级表示较硬挺,3级表示织物柔软;滑爽度类别数越高表示织物越滑爽,1级表示织物手感粗糙,2级表示相对粗糙,3级表示相对滑爽,4级表示织物滑爽;松紧度类别数越高表示织物越松弛,则拉伸易变形,1级表示织物紧致(不易变形),2级表示织物较紧,3级表示一般紧,4级表示织物较松弛,5级表示织物松弛(拉伸易变形)。

图5 聚类结果Fig.5 Clustering results

从织物的柔软度和硬挺度分级情况看,25#试样柔软度为1级(表示织物不柔软),硬挺度也为1级(表示织物硬挺),说明织物的柔软度与硬挺度有很好的一致性,并且柔软度属于5级的试样,硬挺度均属于3级,说明分类结果合理。滑爽度为1级的11#试样为网孔结构,并且表面附有塑料装饰片,手感粗糙,与2级边界织物2#试样相比,2#试样为针织物,表面有线圈使得织物不平整,达不到滑爽程度,但明显没有11#表面装饰片手感粗糙,因此分类结果合理。

2.3 判别分析与预测

2.3.1 贝叶斯判别分析

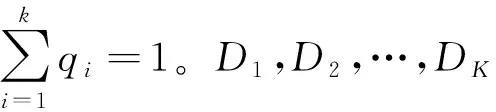
确定样本基本风格指标分类后,将测得织物指标数据结果和分类结果输入SPSS软件,利用SPSS软件进行贝叶斯判别分析,可得到各风格指标贝叶斯判别分类函数的系数,如表4所示,由此可得到4个基本风格指标等级判别函数。将贝叶斯判别分析法得到的结果和K-means聚类分析结果进行对比,没有发现错判等级试样,说明贝叶斯判别分析法对织物风格等级的回判正确率为100%,表现出较高的可信度,可以作为织物风格等级判别的依据。从4个基本风格指标的典则判别函数分类图来看,如图6所示,柔软度和硬挺度59个样本、滑爽度和松紧度60个样本分别按照其基本风格等级聚集在对应类别质心的周围,且可以按不同风格等级区分开来,达到了分类的目的。

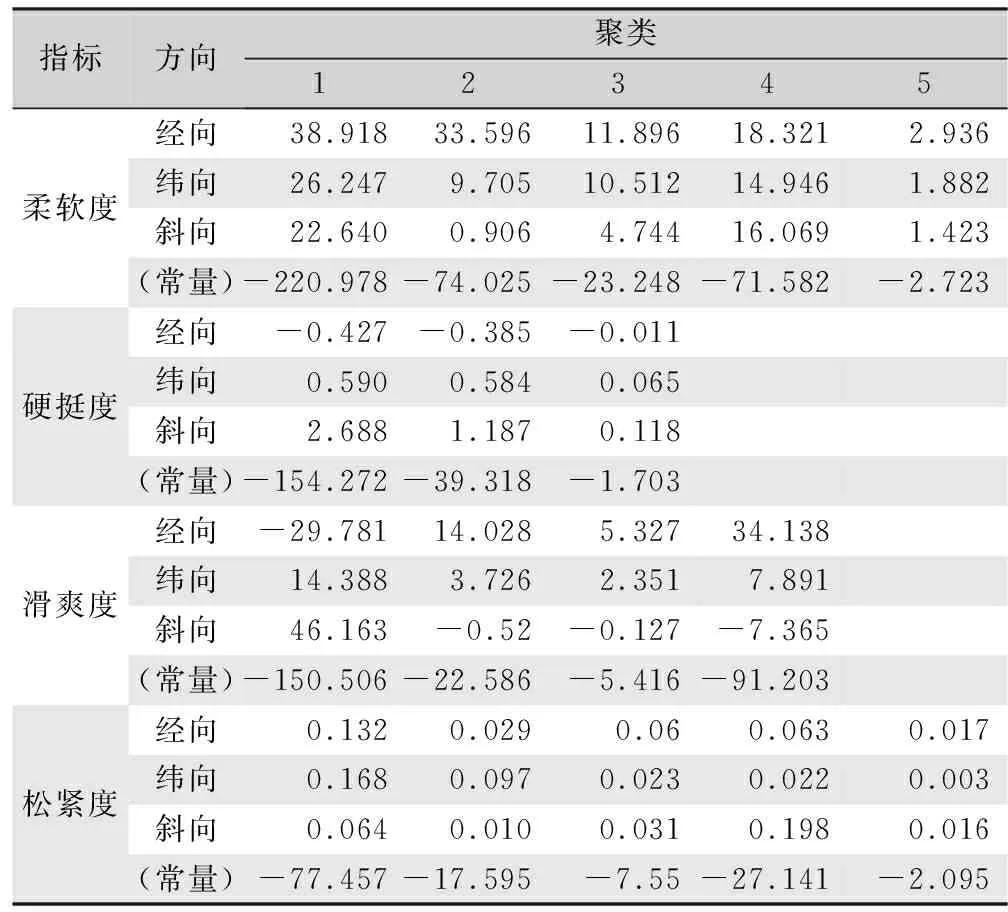
表4 判别函数分类函数系数Tab.4 Classification function coefficient of discriminant function

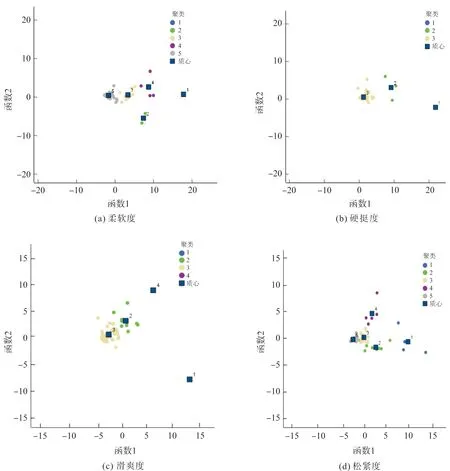
图6 典则判别函数分类Fig.6 Classification diagram of canonical discriminant function

2.3.2 待判试样等级预测

若想知道试样的基本风格指标属哪个等级,只需将各指标结果依次代入对应判别函数,求得函数值,若,则该待判试样基本风格指标判入第k类,其中N为对应风格指标的聚类数,即K值。选取4种试样作为待判试样,编号为A#～D#,试样实物如图7所示。

图7 待判试样实物Fig.7 Physical drawing of sample to be judged

将4种试样的4个基本风格值代入判别函数,得到其基本风格等级,如表5所示。由表5可以看到,A#、B#、C#试样的柔软度均被判定为5级,D#柔软度被判定为3级,4种试样硬挺度和滑爽度均被判定为3级,其中D#试样为较厚实的羊绒机织物,试样压缩丰满性能较好,但不及其他3种较薄织物柔软;A#和B#试样松紧度均被判为5级,表示织物拉伸易发生形变,拉伸弹性较好,其中A#和B#试样均为弹性氨纶针织物,将其松紧度判定为5级合理,C#试样松紧度被判定为1级,C#试样为薄涂层机织物,织物结构紧致,拉伸不易发生形变,将其松紧度判定为1级合理。

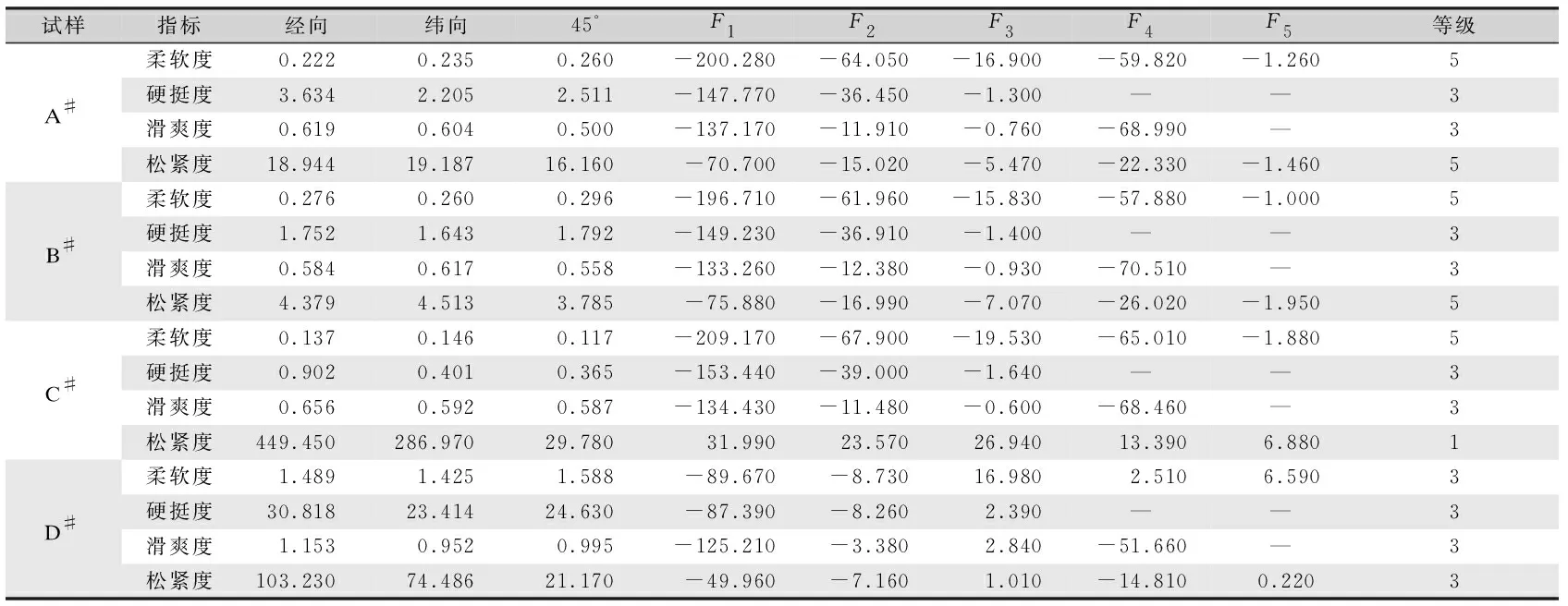
表5 待判试样风格值及等级预测Tab.5 Style value and grade prediction of samples to be judged

3 结论

本文通过CHES-FY风格仪对织物基本风格特征值进行客观测试,运用K-means聚类统计分析方法,综合考虑经向、纬向和45°三个方向的风格特征值,对四个基本风格特征值进行聚类,结合簇内误差法(SSE)和轮廓系数法选取K值,确定了柔软度聚类数为5,硬挺度聚类数为3,滑爽度聚类数为4,松紧度聚类数为5。进一步利用贝叶斯判别法建立了判断织物基本风格等级的判别函数,得到了织物4个基本风格指标等级评价模型,并将待判试样等级带入模型中,得到待判试样基本风格等级值。结果表明基于优选K值结果,使用K-means聚类分析和贝叶斯判别分析用于判别织物基本风格指标等级的方法准确可靠,能够用于织物风格等级评价系统,实现对织物风格等级快速客观评价。