裂缝深度检测的超声波首波相位反转机理分析
2022-10-19肖生玉潘永东
肖生玉,潘永东
(同济大学 航空航天与力学学院,上海 200092)
房屋、码头、水坝、盾构管片等混凝土结构在服役过程中,完整性不断降低,致使结构出现损伤,损伤类型常表现为细裂纹及明显大裂缝。大裂缝常为过载、热胀冷缩、大量细裂纹聚集等因素综合作用所致,其中延展方向垂直于结构表面的裂缝属于亟需诊断的缺陷,因为其所在平面与最大拉应力方向垂直,易迅速扩张导致结构破坏,存在较大安全隐患[1]。同时,水会沿着裂缝渗入混凝土内部,腐蚀结构从而加剧损伤。超声无损检测技术常被用于诊断缺陷和评估工程结构的可靠性和安全性。
BASKARAN[2]结合超声波衍射时差法与隐藏信号识别法,分析时域信号中的衍射横波,评估材料表面垂直裂缝及近表面缺陷的埋藏深度和纵向尺寸。RAMAMOORTHY等[3]提出漫射超声技术,发现超声散射波能量峰值滞后时间与裂缝深度存在二阶多项式函数关系,可利用函数关系反演混凝土的裂缝深度。冯若愚等[4]基于Fourier透射系数法,增加超声波激励源数量对透射函数进行修正,建立起Rayleigh波谱能量透射比与不同裂缝深度的回归关系。
有限元方法提供了直观的视角,可观察超声波在介质中的传播过程及其与缺陷相互作用产生的反射、透射和衍射现象,有助于缺陷的检测与评估。ZHANG等[5]数值模拟了声表面波在圆弧缺陷处的反射和透射,建立起透射表面波飞行时间与圆弧缺陷曲率半径大小的依存关系。金磊等[6]采用有限元方法模拟了激光激发表面波与亚表面缺陷作用的传播过程,为亚表面缺陷的超声检测奠定了理论基础。
上述提到的众多检测方法的应用场景仅局限于实验室或少数高精尖工况,超声波首波相位反转法[7-8]凭借其准确、简单、易操作的优势,收录于标准CECS 21:2000 《超声法检测混凝土缺陷技术规程》 中,并被广泛应用于建设工程质量检测领域。该方法早在1982年由童寿兴学者提出,但其作用机理一直未得到明确解释,人们对首波相位反转的认识只停留在其为一种试验现象的阶段,因此有必要采用理论分析、有限元数值模拟与试验对比法对该问题展开深入研究。
1 超声波首波相位反转法
针对实际工程结构中常见的混凝土表面垂直裂缝,采用“一发一收”方式将压电超声换能器对称布置于开口裂缝两侧近端,如图1(a)所示,向着远端等距同步移动收发超声换能器,使其中心间距L从小至大均匀增加,同时监测接收超声换能器采集信号的首波特征。移动路径上存在一个首波相位发生反转的临界点,对应收发超声换能器中心间距L=L0。当L
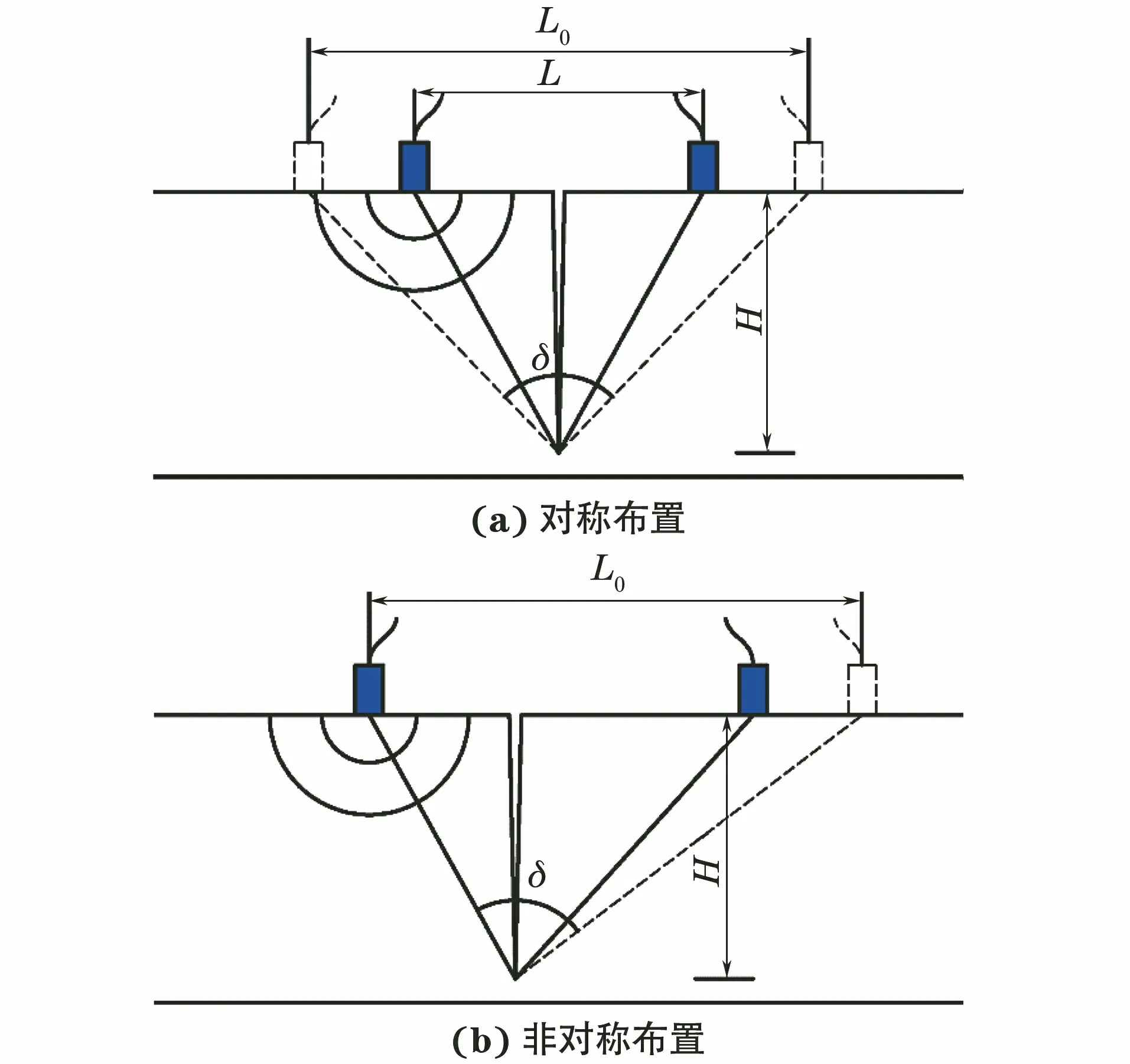
图1 压电超声换能器的布置方式

图2 首波波形的相位反转特征
2 理论分析
建立超声波与裂缝作用的衍射模型(见图3,α为衍射角,β为入射角,θ为方向角),裂缝朝y轴正向无限延伸,并假设其始终保持张开状态,平面波以角度β入射。经Helmholtz分解[9]后的位移场为
u=ux+uy=∇φ+∇×ψ
(1)
式中:u为位移;ux,uy为位移分量;φ,ψ为位移场的拉梅势函数。

图3 裂缝的超声衍射模型
OGILVY等[10]推导了入射平面波经半无限长裂缝发生尖端衍射的解析解,当入射平面波为纵波时,衍射纵波的解析式为
φ=G(α,β)(λp/R)1/2exp(ikpR)
(2)
其中
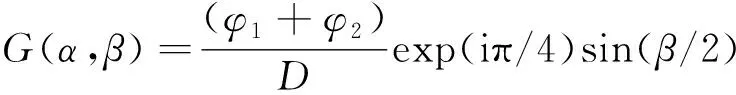
(3)

(4)

(5)
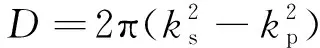
(6)

(7)
式中:λp为纵波波长;R为衍射半径;kp,ks,ko分别为纵波、横波及表面波的波数;G(α,β),φ1,φ2,D,K+(σ)均为过渡变量;x为积分变量。
将表1中混凝土的材料参数代入公式,取入射角β=45°,得到衍射纵波的相位及振幅|G(α,β)|随方向角θ的变化趋势如图4所示。结果表明:存在衍射相位反转角θ0=35°(临界角δ=β+θ0),衍射纵波的相位在此处发生突变,由常值-135°增至45°,相位差为π;在衍射相位反转角θ0附近,衍射纵波的振幅随着方向角θ的增加而呈现出先减小后增大的变化特征。

图4 β=45°时衍射纵波的相位和振幅分布
3 数值模拟
3.1 建立有限元模型
采用多物理场仿真软件COMSOL Multiphysics 5.5进行仿真求解,在均匀各向同性的线弹性固体中,位移场的控制方程为

(8)
式中:ρ为材料密度;u为位移向量;S为应力张量;Fv为可能体积力;t为时间。
在平面应变等效条件下,建立如图5(a)所示的二维半无限平面几何模型,单个周期的Ricker子波[11]以点载荷形式垂直施加于模型上表面中部,其数学表达式为
Ricker(t)={2[πf(t-t0)]2-1}×
exp{-[πf(t-t0)]2}
(9)

图5 混凝土有限元模型
式中:f为中心频率;t0为时间偏移量。
在激励源右侧布置间距为ΔL的3个观测点Re1、Re2及Re3,用于提取声波响应。有限元模型上边界为自由表面,平面左、右及下侧为低反射边界,低反射边界吸收传播至边界的声波,降低波反射及声波模态转换对声场分布的干扰,益于观察声场特征。时间步长Δt及网格尺寸Ld由经验公式(10)和(11)[12]确定。
Δt=1/(20f)
(10)
Ld=λmin/20
(11)
式中:λmin为最小波长。
混凝土材料有限元模型参数如表1所示。
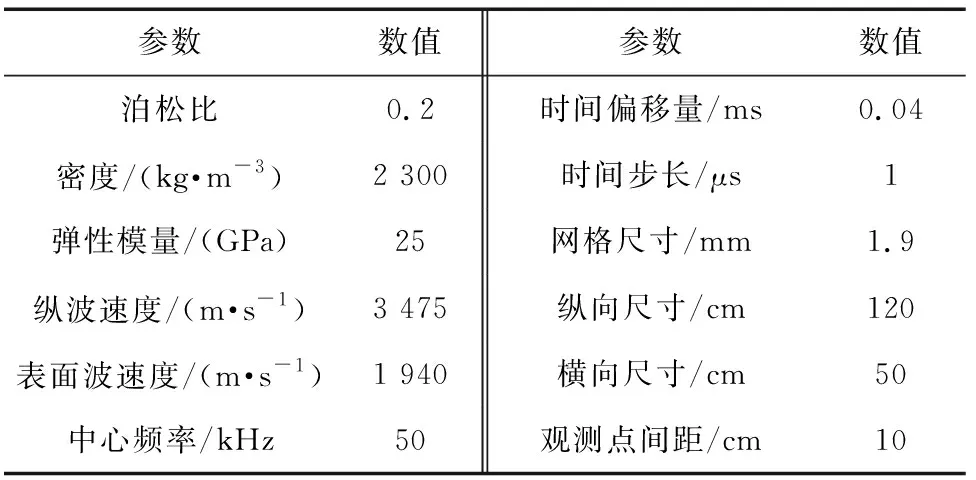
表1 混凝土材料有限元模型参数
各波型的声场分布如图6所示,可见纵波P、头波H、横波S及表面波R可被明显甄别出。观测点Re1、Re2及Re3提取到的位移波形如图7所示,通过位移时差法[13]确定不同声时对应的声波类型(观测点间距为ΔL,声波经过相邻观测点的时间间隔为Δt,由式v=ΔL/Δt可得到声传播速度)。经计算,纵波P和表面波R的仿真速度与理论值一致,分别为3 360 m·s-1,1 929 m·s-1,论证了有限元模型的正确性。

图6 各波型的声场分布

图7 观测点Re1、Re2、Re3处的位移波形
为了探究超声波在带裂缝混凝土中的传播特征和首波相位反转的机理,在上述有限元模型的基础上设置深35 cm的表面垂直裂缝[见图5(b),Lr为观察点到裂纹中心的距离],裂缝开口中心距离左边界60 cm,Ricker子波距离左边界25 cm,裂缝右侧上表面布置有多个观测点,用于提取入射波经尖端衍射后的位移波形。
3.2 数值模拟结果与分析
计算带裂缝混凝土的有限元模型,得到其不同时刻的声场分布(见图8)。结果表明:入射波以柱面波形式向四周传播,速度最快的纵波传至裂缝左端面发生反射和波型转换[见图8(a)],反射波的传播区域局限在裂缝左侧,不会影响裂缝右侧的声场分布;入射纵波在裂缝尖端发生衍射和波型转换,衍射波也以柱面波形式向四周传播[见图8(b)],作为奇异点的裂缝尖端可等效为次声源,这与惠更斯原理[14]吻合;将混凝土划分为Ⅰ、Ⅱ、Ⅲ、Ⅳ等4个区域[见图8(c)],Ⅱ、Ⅲ区域内的衍射波与反射波发生干涉,Ⅳ区域内的衍射波与入射波发生干涉,均使得衍射波成像不纯,相比之下,Ⅰ区域内的衍射波独立传播,可清晰甄别其特征,即衍射头波PH连接衍射横波PS与衍射纵波PP,并与衍射横波PS相切,衍射表面波PR能量微弱表征不明显,速度最快的衍射纵波PP作为首波优先抵达裂缝右侧混凝土上表面。

图8 带裂缝混凝土模型不同时刻的声场分布
值得注意的是,Ⅰ区域内的衍射纵波PP在约45°的方位上存在“扭转带”[见图8(c)中局部放大的A区域]。过裂缝尖端作辅助角γ,其沿顺时针方向从0°增至90°的旋转路径上,衍射纵波PP的成像呈现出“平滑-扭转-平滑”的分布特征。
为明晰原因,提取了裂缝右侧上表面各观测点的位移波形(见图9)。由图9可以看出,衍射纵波作为首波,从形状上看由一对正负波构成,这是激励源Ricker子波带来的波形特征,不影响对首波相位反转成因的解释。记观测点到裂缝中心的距离为Lr,图9的结果表明:存在一个首波相位反转的临界点对应Lr0=40 cm(Lr0为临界点到裂缝中心的距离),在Lr=Lr0处首波相位发生反转,对比该临界点左右两侧Lr=36,43 cm处观测点的首波响应,可以明显看到正波转变为负波;首波的正负波振幅均随Lr的增加而呈现先减小后增大的变化特征,趋势变化转折点也在Lr=Lr0处,对应的衍射相位反转角γ0≈48.8°。

图9 各观测点的首波响应
综上,有限元数值模拟与理论分析的结论一致,这说明首波相位反转法中的相位反转现象是衍射纵波存在衍射相位反转角所致。另需说明,在材料参数相同的情况下,因为在理论分析中假设了平面波入射、半无限长裂缝等简化条件,所以理论分析推导出的衍射相位反转角θ0=35°,不等于有限元数值模拟出的衍射相位反转角γ0≈48.8°,但这并不影响相位反转成因的解释。
这也纠正了童年等[15]学者的研究结果:当裂缝中含有水时,首波相位反转现象会消失,考虑到水中不能传递横波,由此推断相位反转是在特定几何区域内,衍射横波先于衍射纵波到达混凝土表面所致。这是对试验现象的误判。
4 试验验证
素混凝土试块按照C30标准浇筑(见图10),尺寸为500 mm×200 mm×200 mm(长×宽×高),涂抹了润滑油的0.4 mm厚的铁皮用于制作裂缝,裂缝的设计深度为70 mm,检测面上绘制了多个间距为10 mm的测点。采用商用超声仪进行试验,激励电压为1 000 V,采样频率为2 MHz,配备直径为36 mm的50 kHz收发超声换能器。选用凡士林作为耦合剂,将收发超声换能器非对称布置于裂缝两侧,固定发射超声换能器与裂缝的中心距离为100 mm,沿着所绘测点等距移动接收超声换能器并采集信号。采集首个测点(Lr=40 mm)的超声信号时,调大超声仪的增益至首波振幅占满超声仪可视区(衡量声波振幅的纵向尺度)的80%左右,以便于观察首波特征,之后保持增益不变。首个测点的超声信号如图11所示,可以明显观察出首波特征,尽管后续的各波振幅超出了可视区范围,但不影响首波的特征分析。

图10 混凝土试块结构示意

图11 首个测点的超声信号
不同Lr对应的首波信号如图12所示,由图分析可知:存在一个首波相位反转的临界点对应Lr0=80 mm,在该临界点附近首波由正波变为负波;首波的振幅随Lr的增加呈现先减小后增大的变化特征,趋势变化转折点同样发生在Lr=Lr0处;首波相位反转临界点的理论预测值为84 mm,与试验结果近乎一致,在正常的误差范畴内。这与有限元数值模拟及理论分析的结论一致,由此,首波相位反转法中相位反转现象得到了完整且正确的解释。

图12 不同Lr对应的首波信号
5 结语
(1) 基于超声波衍射理论,给出了任意入射角度β下的平面纵波与裂缝发生尖端衍射后的衍射纵波的解析式,其相位及振幅的分布情况表明:存在一个衍射相位反转角θ=θ0,衍射纵波的相位在此处发生突变,相位差为π;在θ0附近,衍射纵波的振幅随着方向角θ的增加而呈现出先减小后增大的变化特征。
(2) 有限元数值模拟的声场分布直观展现了超声波在带裂缝混凝土中的传播过程:入射纵波经过裂缝尖端发生衍射和波型转换,传至混凝土表面的首波是具有不同相位的衍射纵波;衍射纵波存在“扭转带”,对应一个衍射相位反转角θ0,其性质与上述理论分析的结论一致;
(3) 按照C30标准浇筑了带裂缝的混凝土试块,裂缝的设计深度为70 mm,对其应用首波相位反转法进行检测,成功观察到具备上述性质的首波相位反转临界点。
(4) 理论分析、数值模拟和试验验证的结论一致,说明首波相位反转法中的相位反转现象是衍射纵波存在衍射相位反转角所致。对首波相位反转法的完整且正确解释,可为其应用提供理论基础及更有力的数据支撑。同时,超声无损检测技术的应用和研究往往着眼于超声波的振幅、频率和时延特征,而其相位特征因自身的复杂性未得到重点关注,该研究成果为超声无损检测技术的进一步发展奠定了基础。
