“择”最佳时机 “创”最大价值——例谈初中数学实验工具的使用策略*

徐秀峰 (江苏省苏州市吴江区苏州湾实验初级中学 215200)

初中数学实验工具是帮助学生形成数学知识、发展思维能力的重要载体[1]，但是，在实验教学中还存在使用工具时机不对、使用方式生硬、与实验匹配度不高等现象，导致实验效果不理想，学生兴趣不浓.本文结合实验教学典型案例谈数学工具的使用策略.

1 用在兴趣点，增强真实体验

工具相比文字、图片和视频具有直观性、可触摸性等，给学生真实的身体器官体验.“具身认知”理论认为，认识过程离不开身体的参与，在身体和世界反复互动中形成概念和范畴[2].“具身”即身体动作经验，即学习的过程需要身体的参与、动作经验的积累.比如学习几何图形时，可通过创设 多样的体验活动，激发学生做数学的兴趣，丰富对几何图形的直观认识，促进对数学知识的深入理解.

案例1 摸几何体

(1)实验目标：经历“欣赏”“操作”“思考”等活动，认识简单立体图形，能辨析立体图形中的基本元素，感悟实际生活中丰富的几何图形，发展空间观念.

(2)工具介绍：几何体学具.在不透明口袋中放入常见几何体模型，另有棱柱、棱锥的展开纸片.

(3)实验流程：如图1.

图1

(4)实验过程：

①在不透明的口袋中按要求摸出几何体或猜几何体，直观感知几何体的特征，认识面、线、点.

②用纸片折出新几何体(五棱柱、四棱锥)，直观感知新几何体的特征，尝试从点、线、面的角度，辨析新旧几何体的共同属性和差异属性，感悟研究几何图形的方法和路径.

③将五棱柱、四棱锥也放入口袋中，继续按要求摸出几何体，进一步认识几何体的特征，丰富对各类几何体的认识，促进知识的重组和经验的积累.

④尝试按不同标准将口袋中的几何体分成两类，进一步认识几何体之间的区别和联系，建构常见几何体的知识结构.

像这样，借助几何体学具，让学生经历观察、操作、表达、思考等活动，充分调动身体各器官参与，带给学生真实的身体体验，促进学生在多样的活动中认识几何体特征，尤其是两次“摸一摸”的活动，带给学生的不仅是建构知识的过程，而且是积累经验、孕育情感的过程.

2 用在关键点，助力深度研究

实物工具直观、可操作，相比静态图片或视频演示等，能让学生体验变化过程的关系.有些数学实验的结论是抽象的，学生较难理解，有时在实验关键节点使用工具，有助于学生化抽象为直观，借助实物演示发现数学结论，突破思维障碍，促进深度研究.

案例2 钟面上的数学

(1)实验目标：经历转指针、画图形、算角度、定时间等过程，进一步认识钟面上两根指针转速的关系，了解指针转动过程中的数量关系，将钟面角问题转化成一元一次方程问题，感悟转化和模型思想.

(2)工具介绍：每位学生操作一个模拟时钟.拨动指针演示指针运动变化情况，揭示角的形象以及运动变化的情况.

(3)实验流程：如图2.

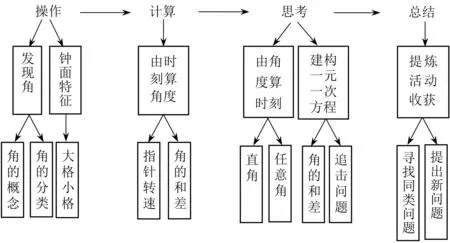
图2

(4)实验过程：

①转动指针抽象出角，经历从活动现象抽象数学对象的过程.

②借助工具理解指针转速的关系，认识角的和差关系.由特殊时刻(数格子)到一般时刻(列式计算)计算所成角大小.

③由角度求时刻.先通过转动指针进行估计，再抽象成角，用角的和差关系列方程解决问题.

④转动指针感悟运动变化，寻找类似运动，感悟指针运动实为追击问题，建立方程模型.

传统教学中观察图片或者动画演示都不能带给学生真实体验，缺乏学生主动参与、自主尝试的过程.让学生操作模拟时钟，经历观察发现、操作感知、交流感悟等过程，在操作变化中认识角，在亲身体验中感受变化，在运动变化中发现结论，有助于认识钟面角的和差关系，建立解决钟面角问题的模型，抽象出一元一次方程模型；从直观到抽象，从实践活动到理性思考，有助于认识数学本质，深化思维发展.

3 用在生长点，促进自然发展

工具使用方式应不拘泥于预设，根据实验进程恰当选择，根据学生情况适时调整，可用在实验发展的生长点，实现实验各环节间的自然过渡，推动实验自然发展，推动学生认识逐级深入.教师应准确把握学生认知基础，理解实验目的和各环节的意图，认识工具的特性和价值.

案例3 算24点

(1)实验目标：经历用扑克牌“算24”的过程，在活动中提高运算能力，促进数感发展，进一步认识“算24”的基本原理，感悟模型思想和转化思想.

(2)工具介绍：磁性扑克牌(按大小分为教师用和学生用).与图片相比，扑克牌可让学生经历触摸、摆放、展示等活动.磁性扑克牌可以吸在黑板上，利于师生互动和展示交流，在多种器官真实感知中促进学生认识发展，激发主动探究的兴趣.

(3)实验流程：如图3.

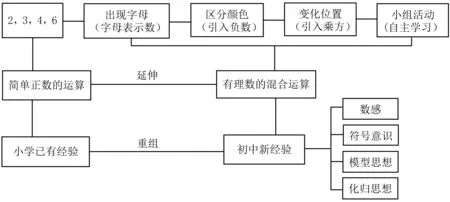
图3

(4)实验过程：

①在完成简单数字计算后，顺势抽出“J”“Q”“K”“A”，提出“字母怎么办”，引入字母表示数，激发符号意识.

②在完成红色牌面数字计算后，将红2换成黑2，提出“同一个数字但颜色不同怎么办”，引入负数，过渡到有理数的四则运算.

③观察颜色变化后所列式子的异同，提问“颜色变化后，所列式子有什么联系”，理解“负 数”的运算可转化成“正数”的运算，感悟化归思想.

④将其中大牌改成小牌，由并排放改成错位放，即将学生扑克牌(小牌)放到教师扑克牌(大牌)的上方，提出“变化位置会想到什么运算？”引入乘方，拓展到有理数的混合运算.

⑤组织小组活动，随机抽牌进行计算，并总结常见算法模型，也认识到存在无法计算的情况.

像这样，在教师或学生“不经意”的动作或提问下，在实验发展的生长节点发挥扑克牌特性，推动实验逐级发展，在变化中感悟所包含的数学问题(有理数的混合运算)，在解决问题中实现数学思维(模型思想、转化思想)的生长.

4 用在疑难点，模拟真实发生

使用工具的价值还应是能解决常规活动不能解决的问题，或者完成不易操作的活动，如实验操作难度大、实验材料复杂、实验次数多等.一些创新的工具可以模拟实验发生，替代实验发展，突破实验开展瓶颈，突破实验疑难之处.

案例4 探索正方体截面的形状(2018年江苏省数学实验总结表彰大会展示课)

(1)实验目标：经历用“水”立方探索正方体截面形状的过程，认识简单平面图形，发展空间观念和简单推理能力.

(2)工具介绍：“水”立方.透明正方体方盒中装有适量水(图4)，用水面模拟截面(依据水量分两种规格以便于出现不同截面形状).相比于用刀切正方体模型，“水”立方能重复使用，没有安全隐患.

图4

(3)实验过程：如图5.

图5

(4)实验过程：

①出示正方体模型，想象用刀切得截面的形状，激发探究欲望.

②出示“水”立方，想象成用刀切，体会工具使用方法和作用.

③分组转动“水”立方，认识截面即水面的形状.

④提出问题“截面可以是七边形吗”“截面可以是哪些四边形”等，引导学生借助工具进行思考，发现确定截面形状的要素，形成数学认识.

⑤提出问题“正四面体的截面可能是什么形状”，类比发现，进一步理解此类问题的本质，发展空间观念.

“水”立方能突破常规工具的局限，真实模拟切正方体的情况，是颇具创新性的数学实验工具.学生在操作中感悟面与面、面与体相交的过程，充分感受、体验三维与二维图形的相互转换，形成、积累图形想象的经验[3].当然，在数学实验过程中也可以应用几何画板、GeoGebra等数学软件，模拟实际操作，提供动态演示和大量例证，比画图、剪拼等常规手段更直观、更丰富，有助于突破学生学习的认知障碍.

总之，数学实验工具有直观、可操作、呈现方式灵活、可创新等特性，能充分调动学生多感官体验，将结果性知识转变成过程性知识，将接受性学习转变成探究性学习.教师要准确把握实验要求和目的，选择使用工具的最佳时机，如数学学习的兴趣点、理解实验的关键点、开展实验的生长点、组织实验的疑难点，充分发挥工具价值，将其作为学习数学、研究数学的有效载体，促进数学实验取得实效，促进学生素养提升.