微孔边缘曲线演化模型的建立与仿真
2022-10-19程锦琳
程锦琳
(北京信息科技大学 仪器科学与光电工程学院,北京 100192)
随着微型机械领域的不断发展,小型化、微型化加工技术已成为新世纪制造领域的一个重要发展方向。特别是在航空发动机的气膜冷却孔[1-2]、光学器件[3]等领域应用广泛。
加工间隙的大小是决定加工质量、效率和精度的核心因素[4]。电解加工间隙受到电场、电解液流场和金属/溶液界面电化学特性等诸多因素的影响,随加工深度、加工时间与电极的进给速度的变化而变化。
国内外研究人员对加工高深宽比微孔间隙的控制进行了深入研究,但时至今日仍缺乏有效手段从理论上给出加工参数与间隙之间的具体关系表达式[5]。如果可以实现对加工间隙和微孔边缘曲线进行预估计,就可以优化和创新间隙伺服控制方法,达到提高微孔精度的目的。
1 加工间隙预估计
首先从电极匀速进给加工测量数据入手,结合加工过程间隙等效电路模型探究加工间隙变化规律,实现对加工间隙的预估计。
1.1 实验数据的测量
采用电极匀速进给的加工方式,使用高频脉冲电源、侧壁绝缘的中空电极在304 钢板上开展高深宽比的微细孔加工实验。测量电极进给速度分别为1~6 μm/s,加工深度分别为50、100、200、300、400、500 μm 时的间隙电流I、间隙电压U 的数值各5 组,并取平均值后绘图。电流、电压数据如图1 所示。
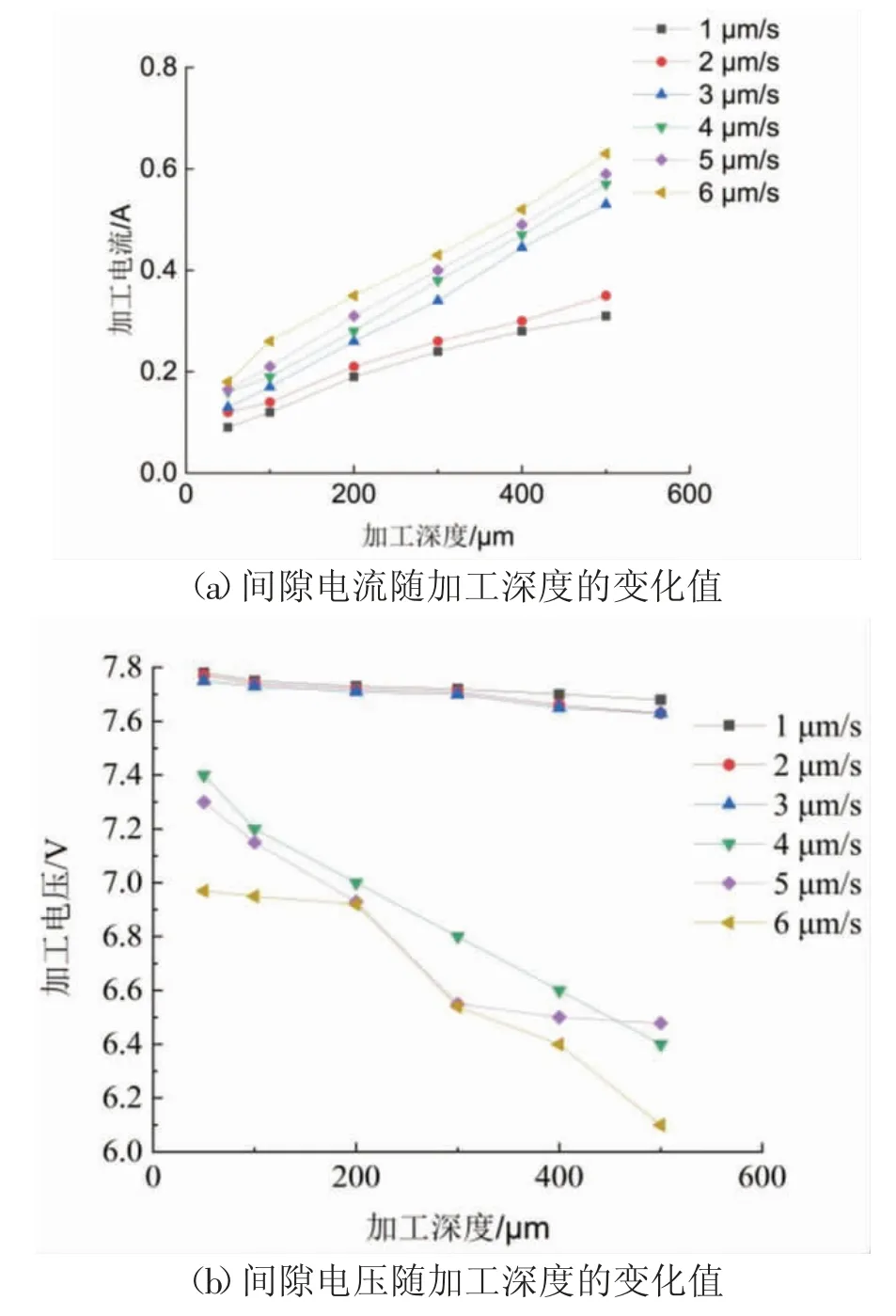
图1 加工过程电流电压值
1.2 加工过程等效电路
金属/电解液界面具有双电层电容,且金属/溶液间双电层电容密度一般在40 μF/cm2左右[6]。
金属电极外壁通过绝缘层介质与加工槽侧壁构成了同轴电容器C3。电极与工件间的电解液等效电阻用R 表示。当电极进给速度为6 μm/s,加工深度为0~500 μm时,加工槽内的双电层电容C2变化范围为22.3~126.8nF。实验中采用的电极侧壁绝缘材料PI 管的相对介电常数约为4,厚度为15 μm。电容C3电容值变化范围为0.46~4.61 pF。电极下端双电层电容C1电容值为2.5 nF。加工状态下间隙加工电路图如图2(a)所示。加工工件作为正极,电极作为负极,经过电容C1与C3和电解液电阻R2串联后再与电容C2和电阻R1并联形成加工间隙电路。C1与C3串联后由于C3远远小于C1,所以串联后其值约等于C3。C3与C2并联后,由于C2远远大于C1,因此并联后其值约等于C2。加工间隙等效电路可以简化为双电层电容C2与电解液电阻之间串联。这一结论在电极进给速度为其他值时仍然成立。
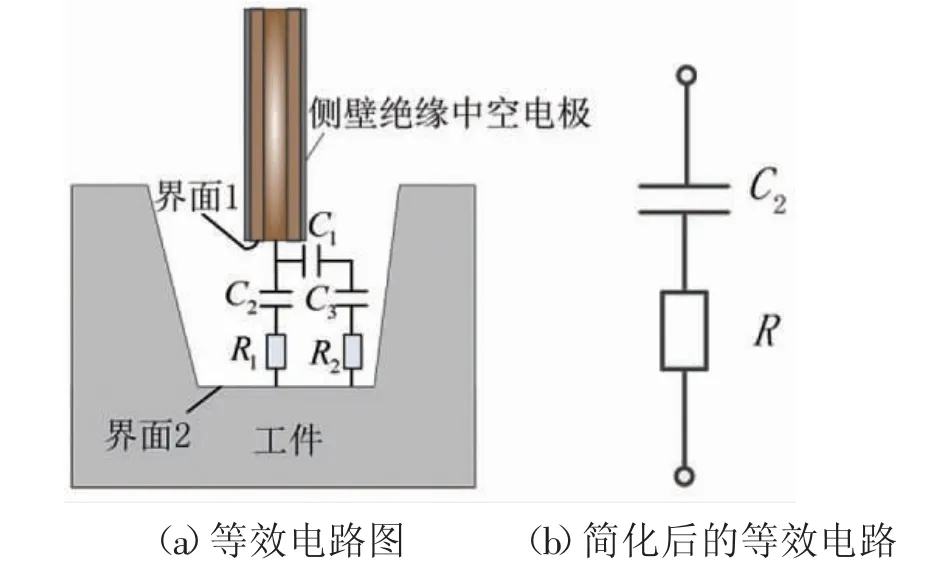
图2 加工间隙等效电路
1.3 加工间隙建模
电解液电阻、双电层电容共同构成了加工间隙等效电路的总阻抗。通过等效电路模型计算出加工过程中容抗值就可求出电解液电阻并进一步推导出加工过程中的间隙大小。根据加工槽内间隙等效电路得出电解槽中电路的总阻抗模值Z 为

式中:R 为加工槽间隙电极液等效电阻,Ω;f 为高频脉冲电源频率,f=100 kHz。将加工槽内的双电层电容C2容抗值,加工过程中间隙电流值I 和电压值U 随加工深度的变化值代入式(1),可得间隙电解液电阻R 随加工深度的变化值,如图3 所示。
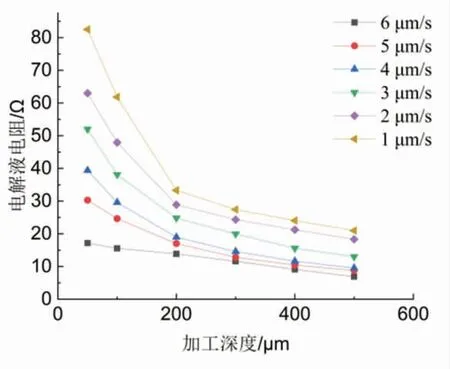
图3 间隙电解液电阻随加工深度变化值
电解质溶液电导公式为

式中:R 为间隙电解液等效电阻,Ω;κ 为溶液电导率;AS为电极下端金属微环面积,μm2;Δyi为纵向加工间隙,μm。
由式(2)可得纵向加工间隙Δyi(t):

电解液电导率为κ=4.8×10-5S·μm-1,电极下端面积为AS=3 846.5 μm2,将图3 间隙电解液电阻R 值代入公式(3)可得加工纵向间隙Δyi随加工高度变化值,如图4 所示。
已知加工时间t 与加工深度h(t)、纵向加工间隙Δyi之间的关系表达式为

式中:νci(t)为电极进给速度随时间变化的表达式,电极匀速进给时为一常数。由式(4)和图4 中纵向加工间隙随加工深度变化的数据可得纵向加工间隙随时间变化值,如图5 所示。
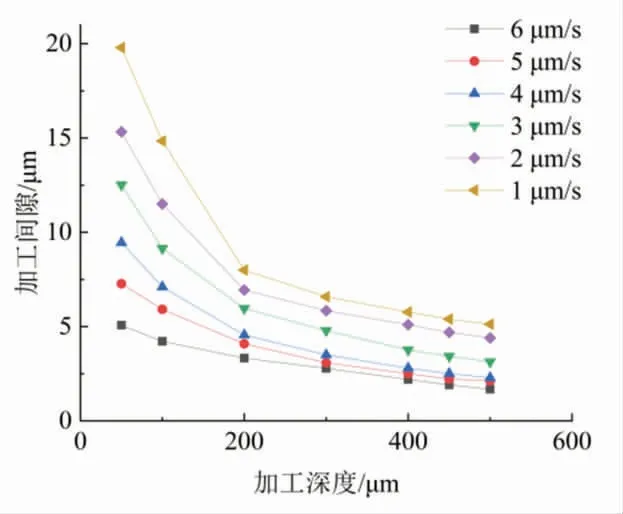
图4 纵向加工间隙随加工深度变化值
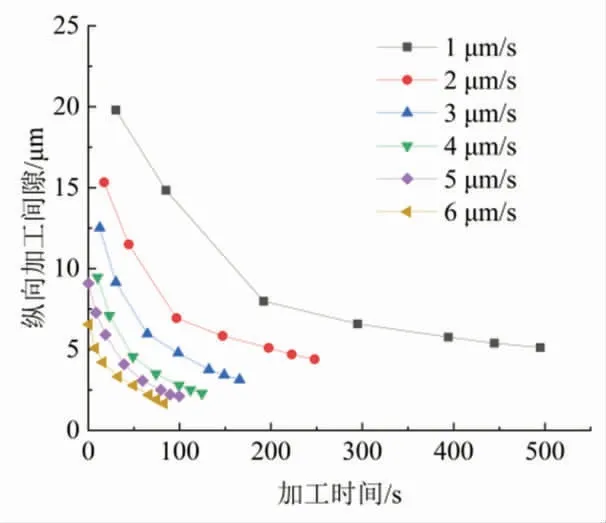
图5 加工间隙随时间变化值
2 微孔边缘曲线演化模型的建立
建立坐标系如图6 所示。在加工坐标系中,x(t)为横向溶解距离,电极半径r1=70 μm,Δxi(t)为加工侧面间隙,Δyi(t)代表纵向加工间隙,νaxi(t)为工件横向溶解速度,νayi(t)为工件纵向溶解速度,h(t)为加工深度。

图6 加工过程坐标系
由于采用侧壁绝缘中空冲液的方式加工微孔,在任意相同tn时刻,电极下端微小的暴露环在纵向和侧壁加工点的电解液流速、电导率等特性相同,加工电压相同,只是对应作用域不同,所以蚀除速度比例固定。不同的tn时刻,纵向和横向加工点的电解液特性不相同,蚀除速度不相同,横向加工速度νaxi(t)和纵向加工速度νayi(t)随加工深度和时间变化。
故设

电场作用于加工微孔侧壁某一点的时间为

式中:Δl 为电解加工实验中加工电场最大作用距离,Δl=30 μm;νci(t)为电极进给速度随时间变化的函数。
加工过程中,加工侧面间隙大小随时间变化的函数为

将式(6)代入式(8)可得

由式(8)可以推出横向加工速度随时间变化函数为

横向加工距离x(t)和加工深度h(t)联立,加工微孔侧壁曲线演化方程为

3 微孔边缘曲线演化模型的仿真
为了验证微孔侧壁曲线演化方程的效果,采用MATLAB 仿真出电极匀速进给速度为1~6 μm/s 时的微孔边缘曲线。
根据微孔侧壁演化曲线画出当电极进给速度为3 μm/s 时,加工微孔形态如图7 所示。随着加工深度的增加,微孔直径逐渐减小,微孔形态呈现为一上宽下窄的锥形,符合实际加工中电极匀速进给微孔形态。

图7 微孔孔型
电极进给速度为1~6 μm/s 时,微孔边缘曲线如图8 所示。电极进给速度越大,加工微孔的半径越小,仿真结果符合实际加工结果。由仿真结果可知,当电极进给速度为1 μm/s 时,微孔入口直径为212 μm,出口直径为187 μm。当电极进给速度为2 μm/s 时,微孔入口直径为206 μm,出口直径为186 μm,微孔锥度为1.15°。当电极进给速度为3 μm/s 时,微孔入口直径为200.5 μm,出口直径为184 μm,微孔锥度为0.92°。当电极进给速度为4 μm/s 时,微孔入口直径为196 μm,出口直径为183 μm,微孔锥度为0.74°。当电极进给速度为5 μm/s 时,微孔入口直径为190 μm,出口直径为180 μm,微孔锥度为0.57°。当电极进给速度为6 μm/s时,微孔入口直径为185 μm,出口直径为178 μm,微孔锥度为0.4°。

图8 微孔侧壁边缘曲线仿真
4 加工实验验证
采用高频脉冲电源、高压中空冲液和侧壁绝缘微细中空电极的工艺,在304 不锈钢上开展电极进给速度为1~6 μm/s 的匀速进给微细阵列孔加工实验。
当电极进给速度为1 μm/s 时,微孔入口直径为212.2~212.6 μm,出口直径为186~186.2 μm。当电极进给速度为2 μm/s 时,微孔入口直径为205.1~205.4 μm。微孔出口直径为185.7~186 μm。当电极进给速度为3 μm/s 时,微孔入口直径为200.8~201.1 μm,出口直径为183.88~184.1 μm。当电极进给速度为4 μm/s时,微孔入口直径为196~196.2 μm,微孔出口直径为182.9~183.1 μm。当电极进给速度为5 μm/s 时,微孔入口直径为192.98~193.53 μm,微孔出口直径为179.56~180.05 μm。当电极进给速度为6 μm/s 时,入口直径为185.12~185.23 μm,微孔出口处直径为177.98~178.05 μm。
5 结论
从电极匀速进给微孔加工实验数据测量入手,通过建立加工间隙等效电路模型得出加工间隙随时间变化值。再使用电极进给速度、工件横向溶蚀速度、加工间隙、加工深度和电极尺寸大小等微孔成型过程变量之间的关系建立微孔边缘曲线演化模型,并仿真出电极匀速进给速度为1~6 μm/s 时的微孔边缘曲线。通过与实际加工微孔尺寸的对比可知微孔边缘曲线演化模型的可靠性较高。
