水动力相互作用对MOB 动力响应的影响研究
2022-10-19张波陈林董明海王化明
张波,陈林,董明海,王化明
(1.浙江国际海运职业技术学院,浙江 舟山 316021;2.浙江海洋大学 东海科学技术学院,浙江 舟山 316022;3.浙江海洋大学 船舶与海运学院,浙江 舟山 316022)
0 引 言
MOB 是一种能够漂浮在海上的多浮体系统,是一种海洋环境、浮体与连接器相互耦合的动力学系统。连接器主要分为柔性连接器和刚性连接器。由于连接器限制了浮体的自由运动,所以连接器承受着极大的载荷。准确预报连接器载荷是目前MOB 研究领域的重点内容之一。和单浮体水动力计算不同,当多个浮体存在于同一流场时,由于物面条件变化将引起流场辐射势和绕射势的改变,这就导致多浮体水动力系数计算比单个浮体复杂得多。
多模块MOB 动力响应的计算方法主要采用频域法和时域法,所采用的计算模型主要有RMFC,RMRC,FMFC 和FMRC 模型。余澜对超大型海上移动基地进行了较为深入的研究,涉及MOB 的动力响应,考虑了浮体水弹性的影响,并进行了实验验证。王永恒等提出由3 个相同模块组成的超大型浮体,研究了不同环境不同连接器刚度下连接器载荷并与试验结果进行了比较,通过比较提出了较为合理的连接器刚度值。宋斌等提出了一种由多个浮式平台合围成的人工港湾式超大型海上基地VLFOB,设计了一种可分离式连接器装置将8 个模块连接成整体。研究了不同连接器轴向刚度对VLFOB 固有频率的影响,得出了连接器刚度的合理范围避免与海洋环境条件产生共振。鲁达以铰接多浮体为研究对象,研究了浪向、波频、阻尼等因素对波浪能发电装置发电功率的影响,并提出了一种用于多浮体水弹性分析的简化计算方法。李志伟以岛礁附近的超大型浮式结构物为研究对象,研究了海底变化对浮体运动响应和连接器载荷的影响,并将数值计算结果与试验结果进行了比较。L.Sun计算了两铰接方形浮式结构物的水动力响应并与Newman 的算例作比较以验证程序正确性,又计算了2 艘大型液化天然气船并排停靠时在波浪中的运动响应和刚性连接器载荷响应。J.N.Newman计算了2 个铰接连接的驳船在波浪中的运动响应,2 条驳船尺寸相同,长40 m,宽10 m,吃水5 m。J.N.Newman 的论文中又提供了另外一个算例,以1,3,5,9,17 个直线排列的圆柱形浮体阵列为研究对象,计算每个圆柱体的波浪力和水动力系数。
1 计算原理
本文研究的MOB 系统由7 个模块组成,模块编号为~,共有12 个连接器,连接器编号为~。整体坐标系和局部坐标系的定义如图1 所示。

图1 MOB(7MS)坐标系定义Fig.1 Coordinate system of MOB(7MS)
当多个模块位于同一流场中时,总速度势表达为:
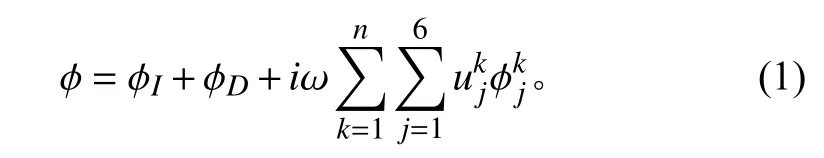
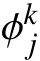
忽略多体间相互影响的刚性浮体柔性连接器模型计算方法与考虑多体间相互影响的计算方法主要区别在于水动力系数矩阵的组成不同。当考虑浮体间相互影响时,第模块第阶辐射力,可表示为:
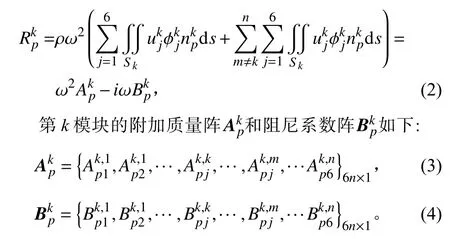

考虑浮体间相互影响时,认为第模块第方向的运动会影响第模块第方向上的力(矩)。如果不考虑浮体间相互影响,则在计算水动力系数时将多浮体系统视为单个刚体。
将个模块的质量矩阵合成一个总质量矩阵,总质量矩阵M和静水恢复力系数矩阵K可以表达为如下:

式中:M为第模块的质量矩阵;K为第模块的静水恢复力矩阵。
连接器载荷为连接器总刚度矩阵乘以连接器位移矩阵,将连接器视为线性弹簧,表达式如下:
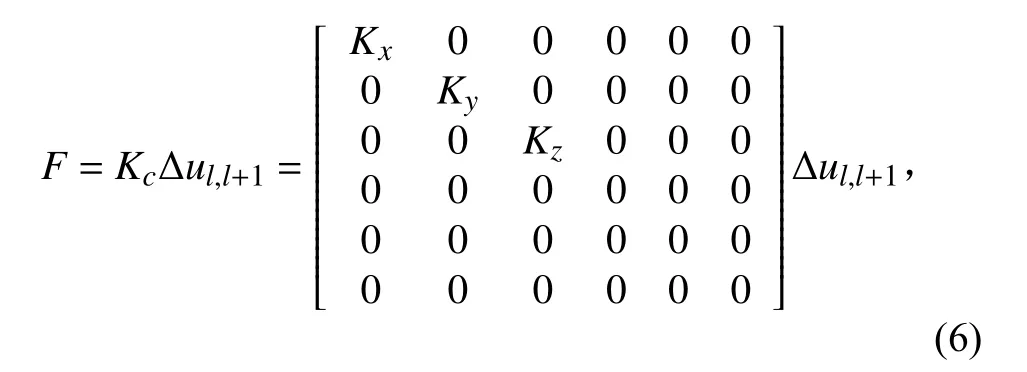
Δu为两相邻模块和+1的位移差。
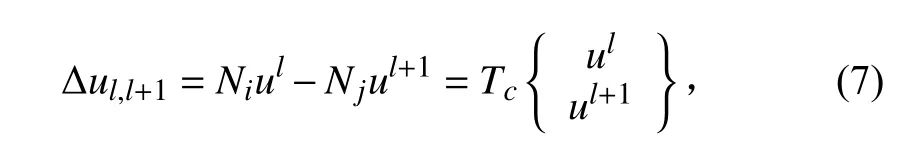
位于第和+1两个模块间的连接器刚度矩阵可表示为:
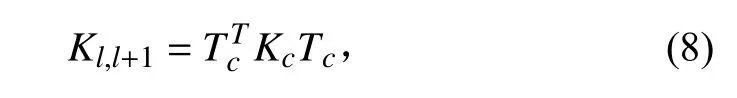
个模块组成的多浮体系统的总刚度矩阵可表示为:
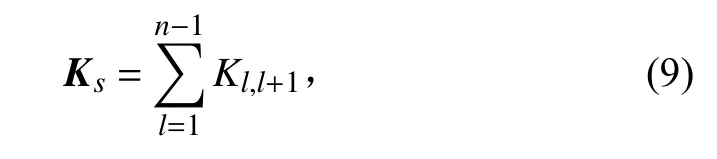
频域下多浮体运动方程的矩阵表达式:
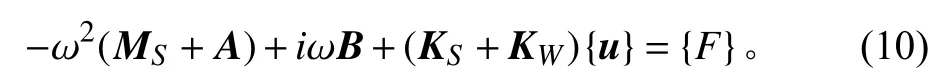
式中:M为系统质量矩阵,6×6;为附加质量矩阵,6×6;为阻尼系数矩阵,6×6;K为连接器总刚度矩阵,6×6;K为静水恢复力矩阵,6×6;和矩阵大小 6×1。
短期预报所采用的波浪谱为Bretshneider 谱,北太平洋开敞海域7 级海况(SS7)的特征波高为7.5 m,谱峰周期为13.8 s。
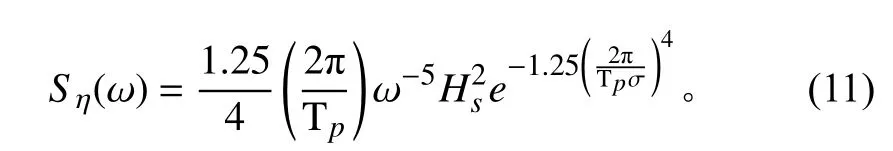
2 计算模型
MOB 浮体模块采用半潜式结构,下浮体长度270 m,设计吃水28.75 m,设计排水量2.975×10kg,方向惯性半径50.412 m,方向惯量半径80.494 m,方向惯量半径90.671 m。网格划分后的MOB 水动力模型如图2 所示。
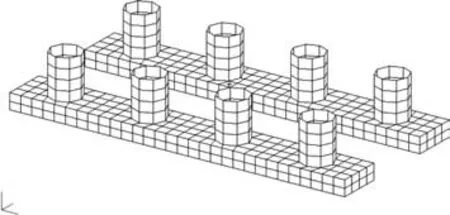
图2 模块水动力计算网格Fig.2 Mesh of MOB module
3 结果与分析
本文计算8 个浪向角(0°,15°,30°,45°,60°,75°,85°,90°),46 个波浪频率(0.1~1.5 Hz),2 种连接器刚度下浮体的运动响应和连接器载荷,并在北太平洋7 级海况下进行短期预报。计算过程中,连接器刚度选择(K=1 0N/m,K=1 0N/m,K=1 0N/m)和(K=1 0N/m,K=1 0N/m,K=1 0N/m)。对采用2 种计算方法得出的结果进行比较时,用“U-”表示不考虑浮体间相互作用时的数值计算结果,“C-”表示考虑浮体间相互作用时的数值计算结果。
本文通过自主开发程序Multifloat 计算MOB 系统的波浪诱导响应。为了验证本程序的有效性,计算了5 模块MOB 系统在连接器刚度 45波浪入射角下连接器的垂向载荷,并与文献[11]中的结果进行了比较(见图3),两者吻合良好。5MS 表示5 个模块组成的MOB 系统。
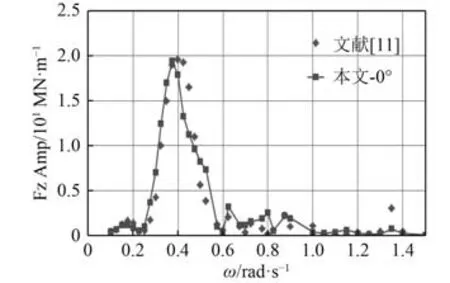
图3 C3 垂向载荷(5MS,K6)Fig.3 RAO of Fz of C3 (5MS,K6)
3.1 波浪激励力和水动力系数矩阵计算
利用水动力计算软件SESAM 计算出考虑浮体间水动力相互作用的波浪激励力矩阵和水动力系数矩阵(主要包括附加质量矩阵、阻尼系数矩阵、静水恢复力矩阵)。图4 为波浪入射角为 0时7 个模块的波浪激励力(矩)RAO。由图可知,不同模块的波浪力(矩)存在一定差别,在特定频率下差别较为显著。由图4(c)和图4 (d)可知,当波浪入射角为 0时,与各浮体的纵摇波浪力矩相比,横摇波浪力矩明显较小但不为零,这可能是由于模块间水动力相互作用导致的。
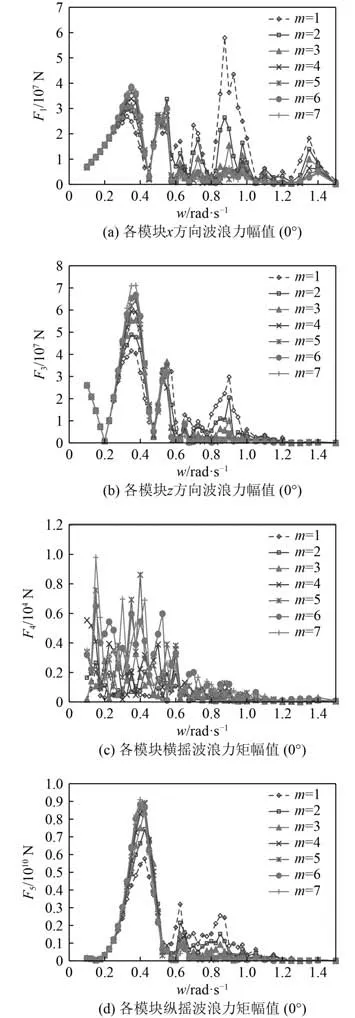
图4 各模块波浪力(矩)幅值Fig.4 RAO of force and moment
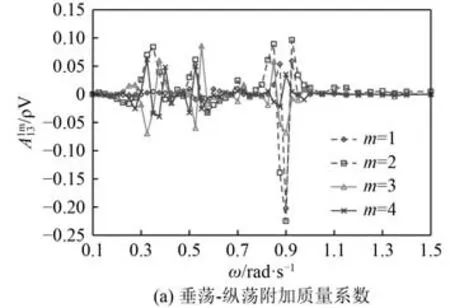
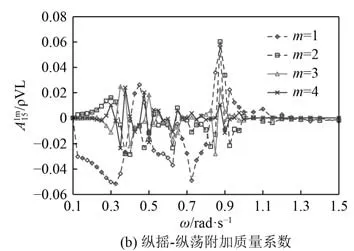
图5 附加质量系数Fig.5 Added mass coefficients
3.2 连接器载荷响应
图6为和刚度下不同波频和波浪入射角度下连接器纵向和垂向载荷幅值图,计算过程中均考虑了模块间的相互作用。由图可知,连接器刚度下,波频在0.3~0.5 之间时连接器载荷值较大,其余频率下连接器载荷较小。连接器刚度下,波频位于0.3~0.5 时,连接器纵向和垂向载荷值较大,当波频为0.475,波浪入射角为 7 5时,载荷达到极值。
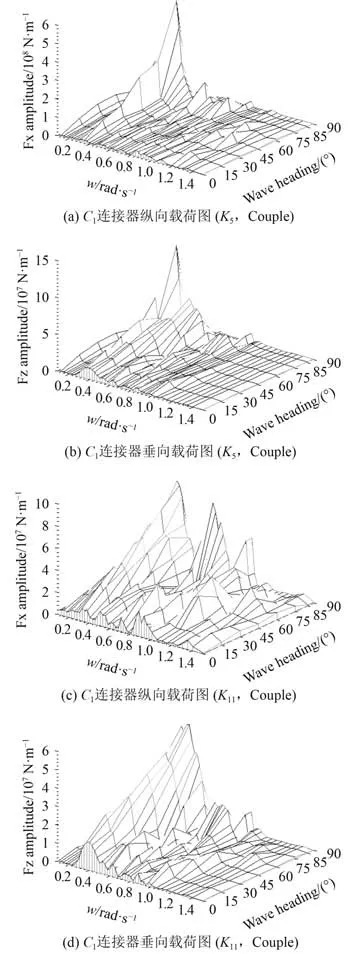
图6 K5和K11 刚度下C1 连接器载荷幅值Fig.6 Load amplitude of C1 under K5 and K11
3.3 模块间相互作用对浮体运动的影响
考虑浮体间相互作用时的计算结果是最为准确的,但是由于求解模块间相互作用的水动力系数矩阵过程较为复杂。为了简化计算,采用不考虑浮体间相互影响的方法进行水动力计算目前也是比较流行的。
不考虑模块间相互作用时得到的计算结果与考虑模块间相互作用时的结果存在一定差别。图7 和图8分别为连接器刚度下采用2 种计算方法得到的模块纵荡和垂荡响应幅值。从图中可以看出2 种方法得出的模块运动值存在一定差别,考虑水动力相互作用时模块的纵荡和垂荡响应极值略大于不考虑相互作用时的值,2 种方法计算得出的模块纵荡响应极值最多相差27.1%。
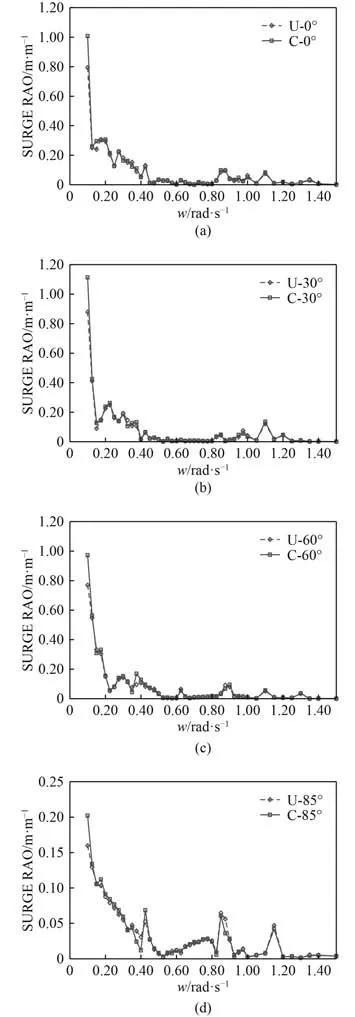
图7 M1 模块纵荡响应幅值(K5)Fig.7 Surge RAO of M1(K5)
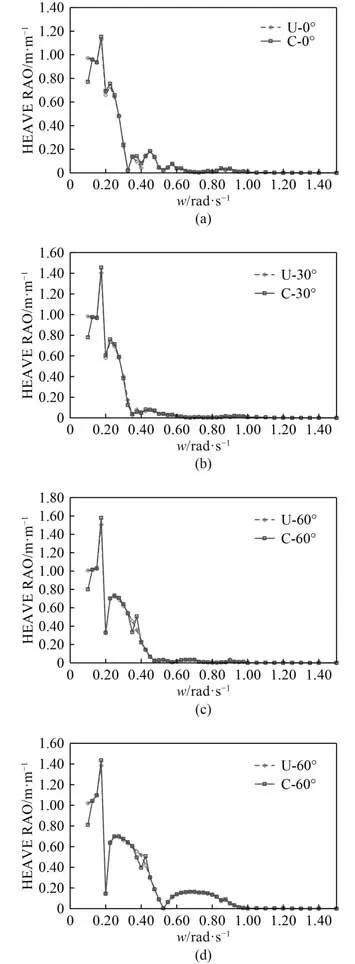
图8 M1 模块垂荡响应幅值(K5)Fig.8 Heave RAO of M1(K5)
3.4 模块间相互作用对连接器载荷的影响
图9 和图10 分别为刚度下连接器纵向和垂向载荷。由图可知,不同波浪入射角度下连接器载荷极值差异较大。在同一个波频下使用2 种计算方法得出的连接器纵向和垂向载荷值存在一定差别,但差别并不显著。
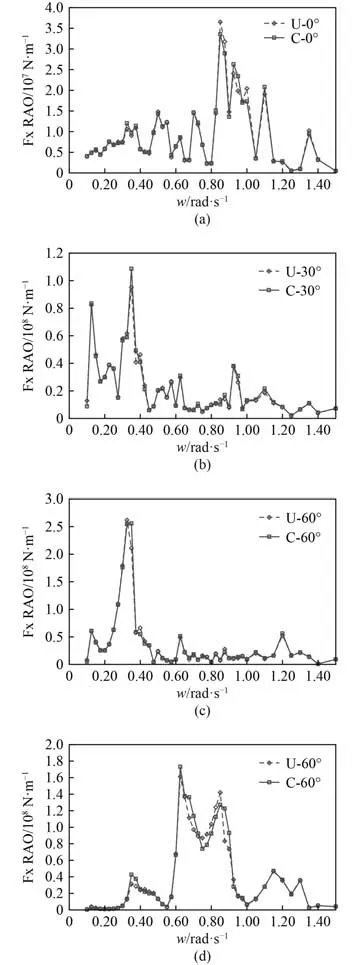
图9 C1 纵向载荷RAO(K5)Fig.9 RAO of Fx of C1(K5)
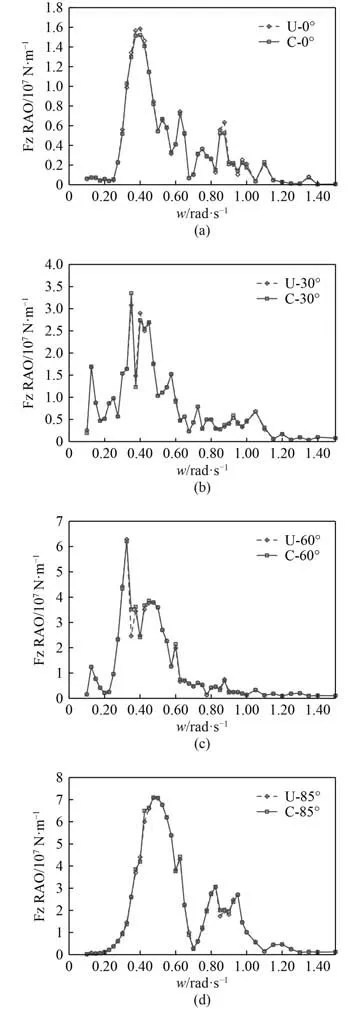
图10 C1 垂向载荷RAO(K5)Fig.10 RAO of Fz of C1(K5)
图11为和刚度时北太平洋7 级海况下和连接器纵向和垂向载荷的短期预报值。由图可知,刚度下连接器纵向载荷极值比刚度时小,但刚度下连接器纵向载荷比刚度时大。当浪向角在 6 0以下时,连接器载荷较小。随着浪向角增大,连接器各方向载荷有增大的趋势,0~ 6 0之间相对平缓,60之后显著增大,并在 75~ 8 5时达到了峰值。采用2 种计算方法得到的连接器载荷短期预报值虽然存在一定偏差,但是变化趋势是一致的。
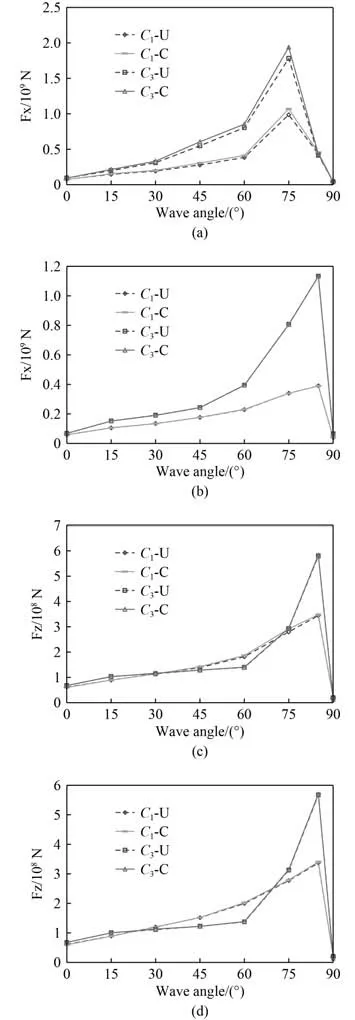
图11 连接器载荷短期预报值Fig.11 Short response of connectors' load
4 结 语
本文利用数值计算方法计算多浮体水动力系数,编程计算了多浮体动力响应,并分析了水动力相互作用对计算结果产生的影响。主要得出以下结论:
1)MOB 系统中2 个相邻浮体间的距离越近水动力相互作用越大,当浮体相距较远时相互作用明显减小。
2)模块间相互作用对MOB 运动响应和连接器载荷存在一定程度的影响。对于不同刚度的连接器来说,模块间水动力相互作用对连接器载荷的影响程度不同。
3)将多浮体系统与波浪入射方向夹角保持在60以下,有利于避开极端连接器载荷。
4)连接器载荷和浮体的耐波性是MOB 初步设计过程中的重要关注点,因此找到一种快速有效的预报方法至关重要。由于采用不考虑模块间相互作用的方法进行响应预报可以大大降低计算复杂程度,且偏差在可接受范围内,所以在MOB 连接器初步设计时不失为一种更为简便的计算方法。
