均匀流下的平台尾流场特征及涡激运动性能分析

陈国庆，张火明，陆萍蓝，余润梁，管卫兵

(1.中国计量大学 浙江流量计量技术重点实验室，浙江 杭州 310018；2.中国计量大学 工程训练中心，浙江杭州 310018；3.国家海洋局第二海洋研究所，浙江 杭州 310012)

0 引 言

深海平台是世界上普遍使用的深海油气田开采装备，这种海洋平其整体尺寸大，服役海域深。将海洋平台置于一定来流中，会在平台两侧交替的产生脱离结构物表面的漩涡，在周围流场压力作用下，平台容易发生涡激运动(VIM)现象。1988 年，Williamson对振荡柱体涡旋泄放结构进行了较为完整全面的实验研究，为之后的涡激振动和涡激运动的尾涡泄放形式研究提供了依据和参考。白治宁等将CNOOC 设计的新型半潜式平台作为研究对象，采用模型试验方法验证动网格技术模拟平台涡激运动的可靠性，得到了较为理想的结果。Rijken在现场和模型试验中观察到半潜式平台涡激运动(VIM)现象，使用CFD 分析获得不同位置数据，显示大部分激励发生的位置。谷家扬等采用雷诺平均法对纳维叶－斯托克斯方程进行求解，将湍流模型和CFD 动网格技术结合起来，研究分析了FDPSO 平台的涡激运动流场特性。

本文利用Fluent 仿真软件中的重叠网格技术，结合涡激运动特征方程求解子程序模拟来流速度在0.02～0.20 m/s（每隔0.02 取一个值）共计10 种工况下Spar 平台的涡激运动情况，捕捉到了涡激运动情况下的流场特征，研究不同约化速度下，影响平台的关键参数和涡激运动过程中发生的锁定现象。

1 理论基础及计算模型

1.1 涡激运动特征方程

实验研究发现，VIM 的运动方向主要为流向和横向，流向表现为纵荡运动，而横向为横荡运动。将平台涡激运动响应简化为弹簧-阻尼-质量系统，如图1 所示。

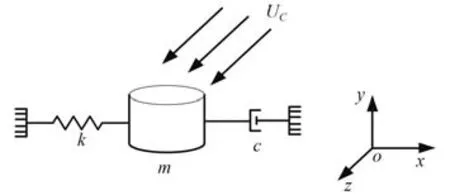
图1 平台涡激运动简化示意图Fig.1 Simplified diagram of platform vortex-induced motion

纵荡和横荡方向上的运动方程可表示为：

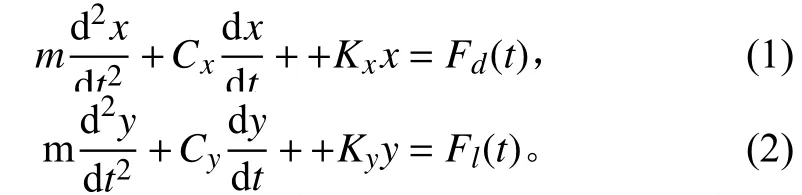
式中：为时间，s；为柱体质量，kg；，为柱体在纵荡和横荡方向上的瞬时位移，m；F()和F()为结构物受到的随时间变化的升力和阻力，N；K 和K是系泊系统刚度；=4πξ f，=4πξ f，分别为纵荡和横荡方向运动的阻尼系数。其中f 和f为平台纵荡和横荡下的固有周期，s；ζ和 ζ分别为平台在纵荡和横荡方向的阻尼比。

DNV-RF-F103 规定，由于顺流向振动幅值的最大值只有横向振动幅值的20%，所以可以忽略平台纵荡运动的影响，仅考虑平台的横荡运动。利用四阶Runge-Kutta 方法对式(2)进行求解，求出每一个时间内流场力和平台的运动位移，经化简后求解，可得横荡涡激运动微分方程的表达式为：

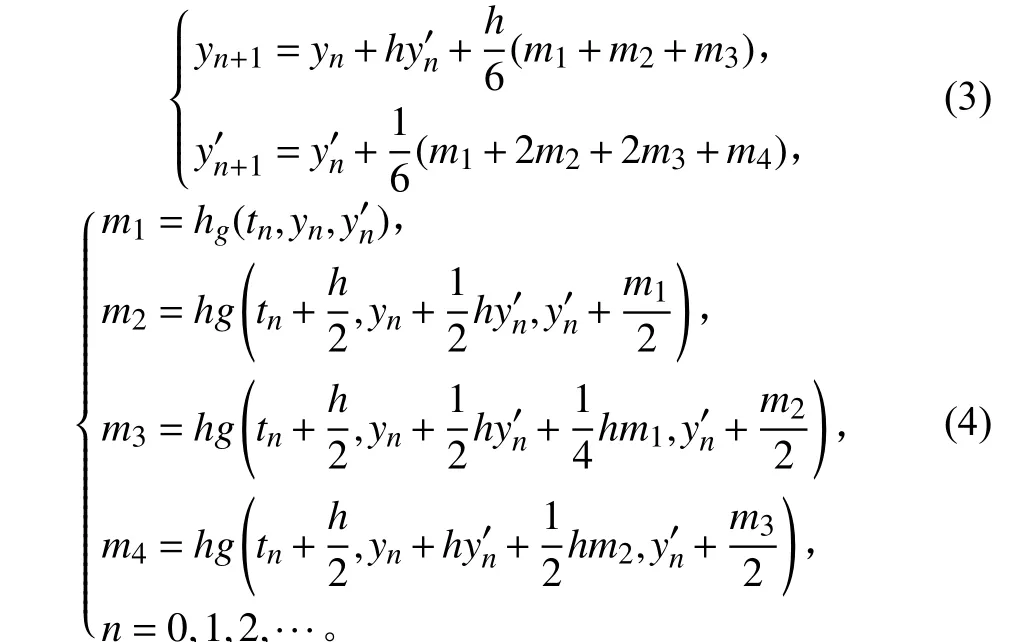
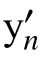
1.2 计算模型

Spar 平台的主体部分（硬舱）为大直径的圆柱体，垂立在水中，在海流作用下，柱体两侧会发生旋涡脱落，引起涡激运动。Koopman和Grifin研究了柱体结构物在振荡流中的响应特征，结果发现当圆柱体的振动频率接近于其自然频率时，圆柱体的涡激运动会抑制尾部涡旋脱落的三维效应，涡旋发放还是二维的，所以采用二维模型足以得出准确的结果。首先，在平台原有尺寸的基础上按缩尺比1:100 建立Spar 平台及矩形流场区域的二维有限元缩尺模型，平台设计参数参见表1。其中横荡运动固有周期通过静水衰减试验得出，模型质量比≈1。

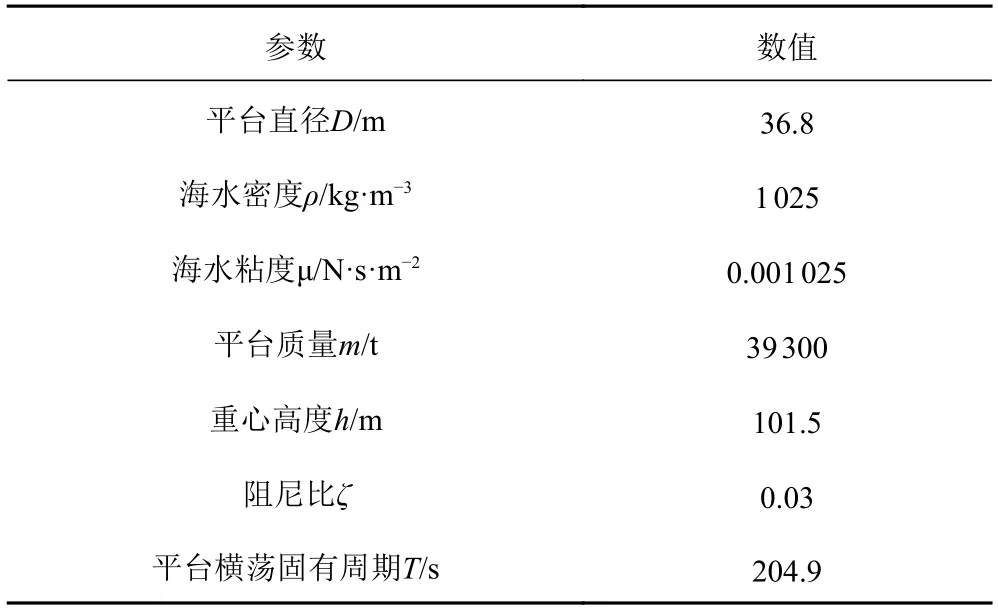
表1 Spar 平台设计参数Tab.1 Spar platform design parameters

图2 为整个计算域模型简图及网格划分模型，将整个流场区域设置为15×40的矩形，边界条件为：左边为速度入口，右边界为压力出口，上下为Symmetry边界条件，平台简化为=0.368 m 的圆柱模型，采用无滑移壁面边界条件。

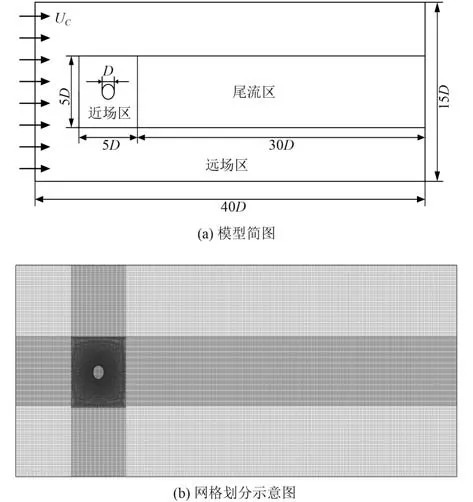
图2 计算域模型简图及网格划分示意图Fig.2 Schematic diagram of computational domain model and meshing diagram

表2 给出了10 种计算工况，来流速度范围为0.02～0.2 m/s，经过表中的公式计算出对应的雷诺数和约化速度U的范围分别为7 360～73 600 和1.11～11.1。后续结果只对U分别为1.11，3.34，7.8，10.2 时的平台升阻力变化情况进行具体分析。

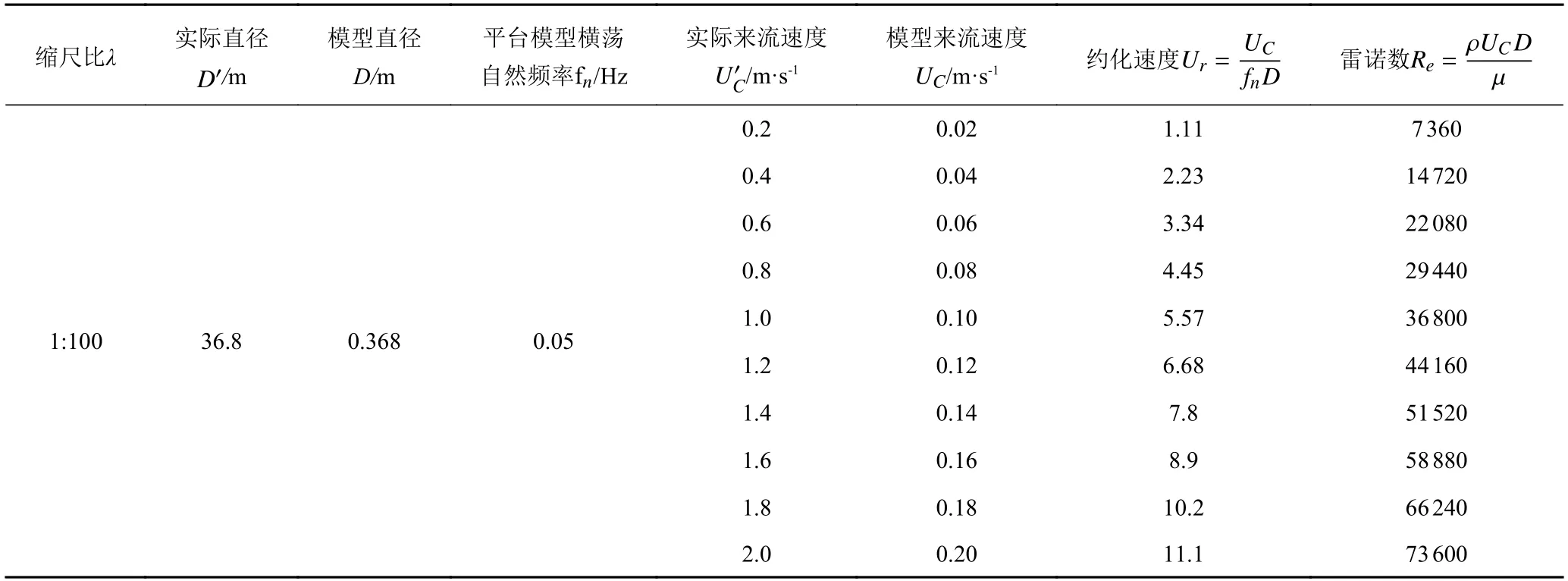
表2 计算工况Tab.2 Calculation conditions

1.3 平台升力FL 和阻力FD

在涡旋的交替泄放的作用下，结构物两侧产生了脉动升力F和阻力F。脉动升力的方向与来流速度方向垂直，脉动阻力的方向与来流速度方向平行，二者是平台产生涡激运动的主要激励力。柱体上端所受的压力要小于下端，垂直于来流速度方向上的升力由此产生，由此涡旋上下交替泄放，脉动升力表现为交变形式，F是Spar 平台涡激横荡运动的主要激励力，脉动升力原理如图3 所示。

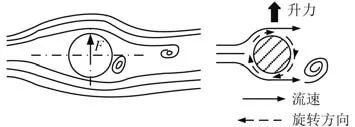
图3 脉动升力产生原理Fig.3 Generation principle of pulsating lift

在对平台涡激运动的激励力进行研究时，一般用无量纲量来表示，其中升力F无量纲化之后为升力系数C，相应地，F经过无量纲化之后为阻力系数C。涡旋泄放的过程中，升阻力具有脉动特性，考虑将升阻力系数分成时均和脉动2 种情况，时均下升力系数C一般为0，用脉动升力的均方根来计算得出脉动下的升力系数，时均阻力系数，脉动阻力系数如表3所示。

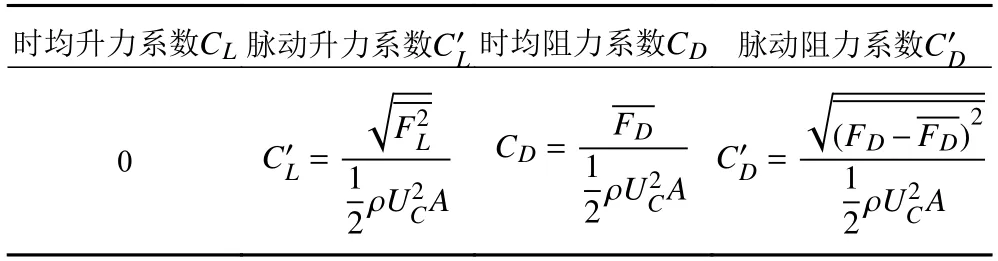
表3 Spar 平台升力系数，阻力系数和脉动阻力系数Tab.3 Lift coefficient,drag coefficient and fluctuating drag coefficient of Spar

1.4 网格无关性验证

取来流速度0.1 m/s，=36 800 情况，采用SIMPLIC 求解器对网格数量分别为Mesh1，Mesh2，Mesh3，Mesh4 和Mesh5 等5 种情况下平台的绕流状态进行有限元仿真，并将计算结果依据施特鲁哈尔数St 相互比较，结果如表4 所示。可知，当网格数增加到Mesh3(95 360)时，其升阻力及斯特朗哈尔数几乎不再变化，为节省计算资源，选取Mesh3 网格数作为本次数值模拟的网格数。

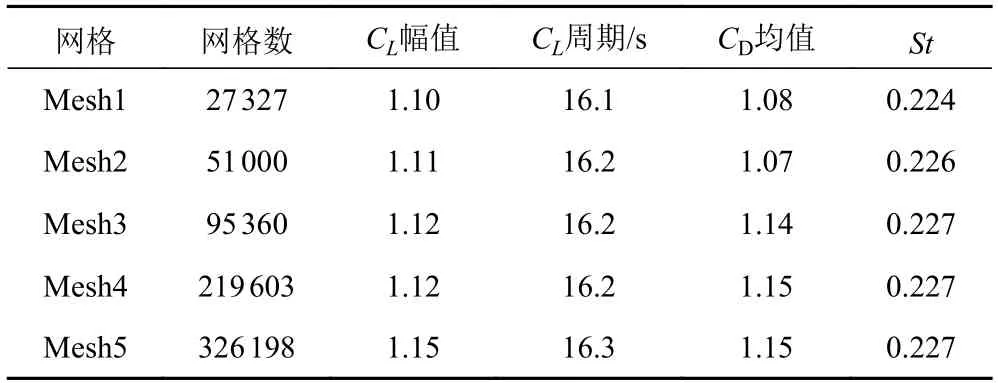
表4 网格无关性验证Tab.4 Grid independence verification

2 计算结果分析

2.1 Spar 平台尾流场特征

图4 为约化速度U为1.1～11.1 时，平台发生涡激运动时某一时刻的尾流场。从图4(a)中可以看出，涡旋泄放的模式为2S 模式，与静止绕流状态下的形式相差不大，涡旋都呈上下相互交替泄放的形态；图4(b)中平台后方的涡泄形式与图4(a)中的形式发生了本质的变化，涡旋出现在平台中心线上下对称位置，形态由图4(a)中的“单排”转变为到“双排”，这主要是由于平台横荡运动幅值增加所导致的。该涡旋泄放的模式为2 P 模式，随着约化速度的逐渐增大，尾流场后方出现了一些小型的碎涡，且碎涡的出现位置不固定，说明了平台涡激运动具有随机性；在平台后方的湍流流动得到充分发展后，湍流强度慢慢增加，尾流区域的涡旋形状由开始的规则形状被破坏，变得小且不规则。

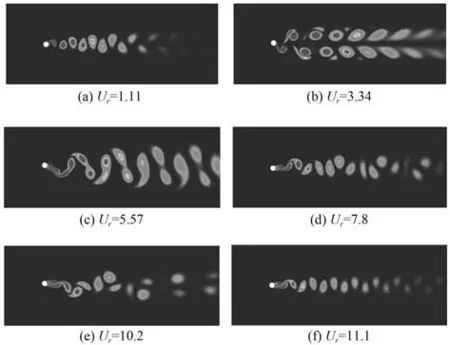
图4 不同约化速度时平台的尾流场Fig.4 The wake field of the platform at different reduced speeds

2.2 平台静止情况下 CD、CL变化情况

图5 给出了平台在不同约化速度下升阻力系数时历变化曲线和升力系数经过傅里叶变换之后得到的FFT 图谱。从升阻力系数时历曲线图可以看出，升阻力系数均呈现出周期性变化的趋势，C周期大约为脉动C周期的一半，来流速度的增加使得旋涡脱落频率增加，升阻力系数的变化周期也相应缩短；C均值趋近于0，这是因为流场流过平台产生的涡旋具有对称性且上下涡旋脱落频率大致相同所导致的结果。FFT分析图谱中给出了脉动升力的频率分布图，C频率为单一的窄带状，在平台静止绕流中，涡旋泄放的频率与脉动升力的频率一致，且随着约化速度的增加，平台最大升力时对应的频率也在逐渐增大。

图5 不同约化速度 Ur 下的 CL，CD 曲线图和FFT 分析Fig.5 Analysis of C L，CD curves and FFT under different reduced speedU r

图6(a)～图6(c)分别给出了不同来流速度下最大升力系数幅值和阻力系数均值曲线以及涡旋泄放频率图，可以看出本文所采用的计算模型得出来的结果与文献所计算的差别不大。在约化速度U为0.02～0.2 m/s 范围内，随着U的增加，升力系数幅值C和阻力系数C均值相应的减小，不过在U=0.1 m/s 时，C和C减小的速度下降，不像之前速度变化快，而涡旋泄放频率f与U成正比，呈现上升的趋势。为了更加直观展示出C与C的关系，图6(d) 给出了来流速度在0.1m/s 下的C与C的轨迹线，可以看其轨迹线呈歪“8”字形。这也从流体激励的方面解释了涡激运动中横荡与纵荡的轨迹线呈“8”字形的根本原因。

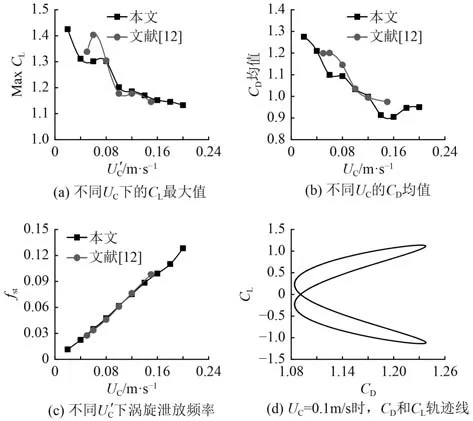
图6 平台在不同 U C 下的 CL，CD及其轨迹线Fig.6 C L，CD and their trajectories of platform under differentU C

2.3 C D和CL及A 变化情况

图7(a)～图7(d)为不同约化速度下，平台发生涡激运动时的升阻力系数随时间变化的曲线和无量纲振幅及其相对应的FFT 分析（最大无量纲振幅的值取涡激运动达到稳定之后的值）。在约化速度为1.11～10.2 范围内，不管是哪一个约化速度下，无量纲振幅比的值都跟升力系数的幅值紧密相关。在达到一定时间之后，升阻力系数都会呈现出周期性的变化规律，升力系数变化的幅度较大。随着约化速度的增大，涡激运动下的升阻力系数变化规律与静止绕流状态下的变化规律一致，都是出现减小的趋势，U从3.34 开始，C幅值相较于静止绕流状态出现大幅度减小的现象，且无量纲振幅比的值时而增大时而减小。这表明，平台由静止绕流状态进入涡激运动状态，平台受到涡激运动的影响，横向升力幅值减少，平台涡激运动开始进入锁定状态。当U＞3.34 时，频率图谱中出现了2 个能量比较集中的频率带：一个为平台的振荡频率，另一个为平台的自然频率；当U=7.8 时，频率的2 个极值最明显，能量最为集中，平台振动幅度也相对较大；当U＞7.8 时，无量纲振幅比急剧减小，说明平台脱离锁定区。

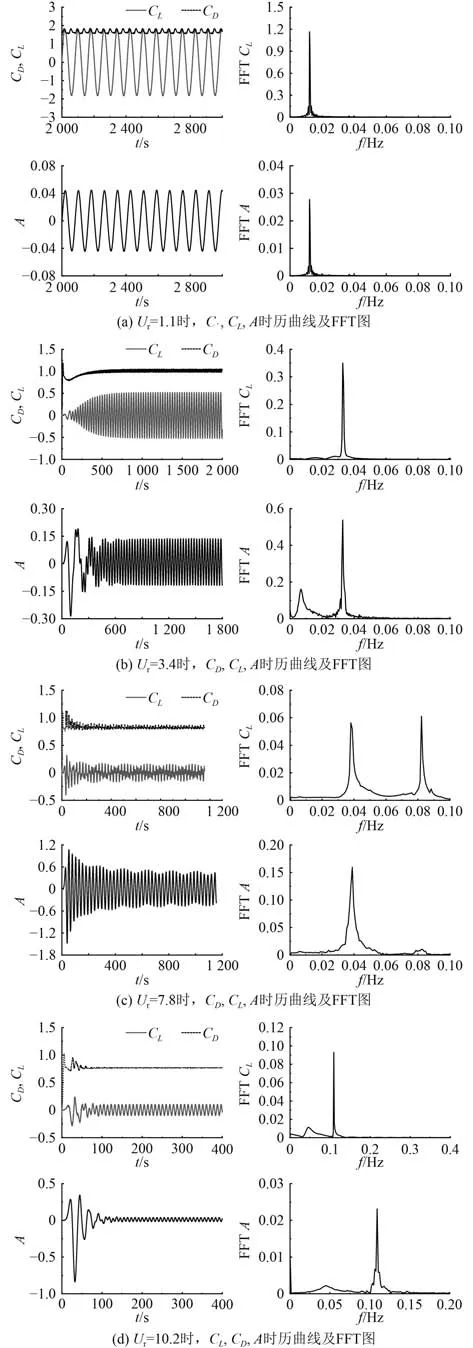
图7 不同 Ur 时的 CL,C D,A 时历曲线及FFT图Fig.7 Time history curves of C L,C D,A and FFT chart at differentUr

2.4 频率锁定现象

在涡泄频率接近平台固有频率时，平台涡激运动的频率比(f/f)被锁定在约等于1 的位置，在一定的来流速度范围内，涡泄频率不再随着U的增加而增加，这种现象被称为频率锁定。在均匀流场中的柱体发生涡激振动或者涡激运动的状态可分为锁定状态、过渡状态以及非锁定状态3 种。其中，过渡状态又可根据与锁定状态的关系分为上阶段和下阶段，从非锁定状态进入到锁定状态这一阶段称为下过渡阶段，经历过锁定状态到离开锁定状态这一范围称为上过渡阶段。图8 和图9 给出了利用重叠网格技术计算出来的不同约化速度下的频率比和无量纲振幅比的最大值。通过与文献[12]模型试验的结果比较，大部分数据点的误差都在10%之内，间接证明了利用Overset Mesh 技术对涡激运动中流场信息进行更新的可行性和准确性。图8 中，f为平台静止状态下的涡泄频率，f为平台在涡激运动下的涡泄频率，f为平台的自然频率。

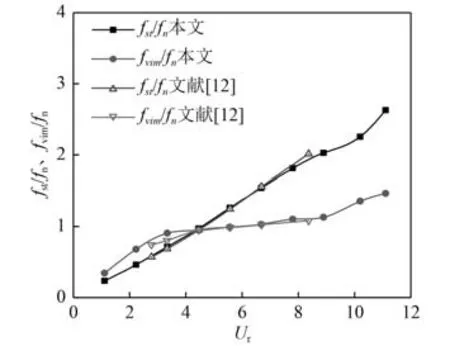
图8 不同约化速度 Ur 时的频率比Fig.8 Frequency ratio at different reduced speedsU r

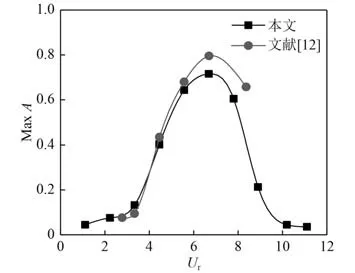
图9 不同约化速度 Ur 时的无量纲振幅比最大值AFig.9 The maximum value of dimensionless amplitude ratio A at different reduced velocitiesU r

从图8 可以看出，平台静止绕流状态下的频率比与约化速度之间呈现出线性递增关系，并且涡泄频率f随着约化速度的增加而增大。结合图8 和图9 分析得出：当平台发生涡激运动且约化速度1.11＜U＜3.34 时，下过渡阶段平台的运动幅值非常小，大约为0.05；当U达到3.34 之后，涡泄频率f与平台自然频率f相接近，频率比大约为1，锁定现象开始发生，无量纲振幅比大幅度增加；当U=6.68 时，无量纲振幅比达到了最大值，为0.7左右；当U=3.34～7.8 时，锁定区域内的涡泄频率f不再随着约化速度U的增加而增加，而是被锁定在平台的自然频率上；当7.8＜＜11.1 时，上过渡阶段的涡泄频率开始高于平台的自然频率，平台涡激运动脱离锁定区域，无量纲振幅比也急剧减小。所以在进行平台结构设计时，要充分了解平台所处的海洋环境，避免或者减小平台在所处环境海流作用下的频率锁定概率，减小其振动幅度，保证平台安全性。

3 结 语

本文利用四阶Runge-Kutta 方程求解Spar 平台涡激运动中横荡运动微分方程，根据表达式编写涡激运动子程序，结合重叠网格技术对涡激运动流场进行更新。通过数值模拟方法捕捉到平台在来流速度U=1.11～11.1 范围内的流场特征，得到以下结论：

1) 通过与文献[12]模型试验的结果相比较，采用Overset 重叠网格技术计算得到的无量纲振幅跟频率比的误差都控制在10%之内，捕捉到的涡旋泄放图像较为清晰。表明在模拟平台涡激运动时，重叠网格技术完全可以用于模型的网格划分，并且能够克服动网格重构问题；

2) 平台涡激运动历经一定时间之后，阻力系数C和升力系数C呈现出周期性变化的规律，并趋近于稳定。随着约化速度的增加，无量纲振幅比的值时而增大时而减小。当U大于3.34 时，频率图谱中出现了2 个能量比较集中的频率带；当 U=7.8 时，的频率2 个极值最明显，能量最为集中。在平台设计时，要考虑外部环境可能引起的涡激运动，通过改变平台的结构参数减少涡激运动的影响；

3) 涡旋在Spar 平台的硬舱两侧呈现上下相互交替泄放的形态，且关于平台中心线对称。随着约化速度的增加，平台后方的旋涡泄放由2 S 模式逐渐演变为2 P模式，形态由“单排”转变为“双排”，尾流场后方出现了一些小型的碎涡，碎涡的出现位置不固定，说明了平台的涡激运动具有一定的随机性。