基于黏滑扭振的地铁小半径曲线钢轨波磨形成机理
2022-10-18王志强雷震宇
王志强 雷震宇
(同济大学铁道与城市轨道交通研究院, 上海 201804)
钢轨波磨是钢轨表面形成的纵向周期性不平顺现象,对于地铁线路而言,钢轨波磨大多为短波波磨,波长主要为30~100 mm[1-6].钢轨波磨是一种复杂的滚动接触物理现象,涉及影响因素众多,是轨道交通行业尚未彻底解决的难题之一,因此探究钢轨波磨的形成机理显得尤为重要.
目前,世界范围内关于钢轨波磨的研究较多,主要包括现场测试、数值仿真和理论分析[7-14].Liu等[15]基于摩擦自激振动理论模型,分析了实测地铁线路钢轨波磨的产生机理.周志军等[16]针对地铁轨道短波波磨现象,采用力锤法和有限元法,研究了短波波磨与轮轨结构动态响应的关系.Balekwa等[17]通过试验测试、有限元模态分析和复特征值分析,研究了牵引轮对和轨道的动力学特性.李响等[18]认为梯形轨枕轨道固有振动属性和车辆通过速度是导致波磨的关键因素.Fourie等[19]利用复模态理论,发现牵引电机和轮对的耦合模态是造成轨道短波波磨的原因.Chen[20]研究了轨道曲线半径对轮轨滑移的影响,得出曲线半径越小,钢轨波磨越容易出现.Wang等[21]研究了多个车轮与钢轨之间的振动波干涉引起的波磨增长.Kaewunruen[22]介绍了使用动态轮轨相互作用来监测小半径曲线钢轨波磨增长的方法.Zhang等[23]通过现场观察和测量,发现列车/轨道在主频处的动力相互作用是钢轨波磨产生的原因.Andersson等[24]提出了一种预测钢轨波磨的方法,发现高波磨增长率对应于列车-轨道耦合系统的特定激振模态.
由上述文献调研可知,轮对/轨道振动或轮轨系统耦合振动被认为是造成钢轨波磨的主导因素,但是振动是轮轨系统的宏观表现形式,而钢轨波磨发生在轮轨接触斑区域,属于轮轨微观磨耗行为,因此,振动角度难以直接反映钢轨波磨的形成过程.鉴于此,本文从轮轨微观接触层面出发,提出了一种新的基于轮轨黏滑扭振的钢轨波磨形成机理,并利用上述理论很好地解释了实测小半径曲线区间的钢轨波磨现象.首先,根据现场测试,获得了线路上钢轨波磨的主要特征波长;然后,通过建立车辆-轨道刚柔耦合动力学模型和多轮对-轨道三维实体有限元模型,分析了车辆/轮对通过曲线时的轮轨黏滑扭振特性,并对波磨成因进行了解释;最后,针对轮轨黏滑扭振的形成机制,展开了进一步的研究,结果发现超高状态影响着曲线轨道轮轨黏滑负斜率的形成机制,从而决定了钢轨波磨的发生概率.
1 实测线路钢轨波磨
1.1 线路基本情况
实测线路为天津地铁6号线乐园道—尖山路区间,线路里程为DK31+947.606 ~ DK32+805.471.上述区间于2018-04-26开通运营,列车采用6B编组,最高设计速度为80 km/h,该区间道床结构型式如表1所示.
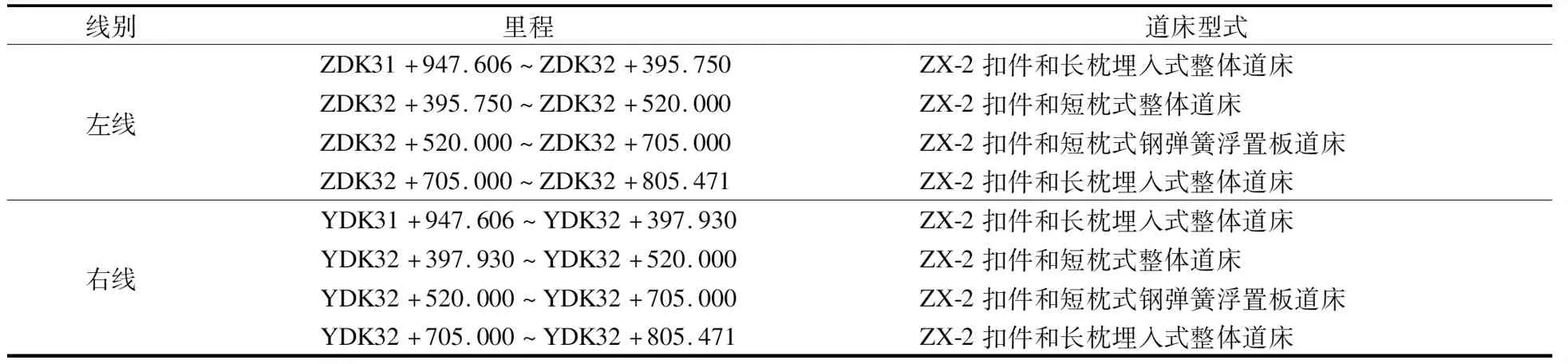
表1 道床结构型式
乐园道—尖山路区间包含一段半径为350 m的小半径曲线,左线曲线长度为611.742 m,最大超高为120 mm,里程为ZDK32+111.998 ~ ZDK32+723.740;右线曲线长度为596.742 m,最大超高为88 mm,里程为YDK32+129.098 ~ YDK32+725.840.通过现场调研发现,该区间内轨轨面波磨发生较为频繁,外轨部分区段存在侧面波磨,波磨现场照片如图1所示.

(a) 内轨轨面波磨

(b) 外轨侧面波磨
1.2 实测波磨分析
钢轨波磨是一种周期性的轨道不平顺.实际线路上存在的轨道不平顺是由不同波长、不同相位和不同幅值的随机不平顺叠加而成的,是与线路里程和运量有关的复杂随机过程,因此不能仅从波长和波深2个数据指标对波磨进行评价,而必须采用随机理论中的统计参数来描述.本文利用钢轨表面粗糙度级Lr这一指标对测试区段钢轨波磨进行分析,该指标采用1/3倍频程波长谱的形式表达钢轨波磨的程度,计算公式如下:
(1)
式中,rrms为钢轨表面波磨幅值有效值,μm;r0为钢轨表面基准粗糙度级参考值,r0=1 μm.
波磨现场测试采用CAT波磨采集仪,分别测试上下行区间的内外轨.该设备采用惯性基准原理进行测量,探头紧贴钢轨表面进行数据采集,测量重复性不低于1 μm,测量分辨率高于1 μm,数据采样间隔为2 mm,测量速度为0.8~1.2 m/s.测试起终里程与对应数据里程如表2所示,实测钢轨不平顺幅值随数据里程的变化曲线如图2所示.

表2 实际里程与对应数据里程
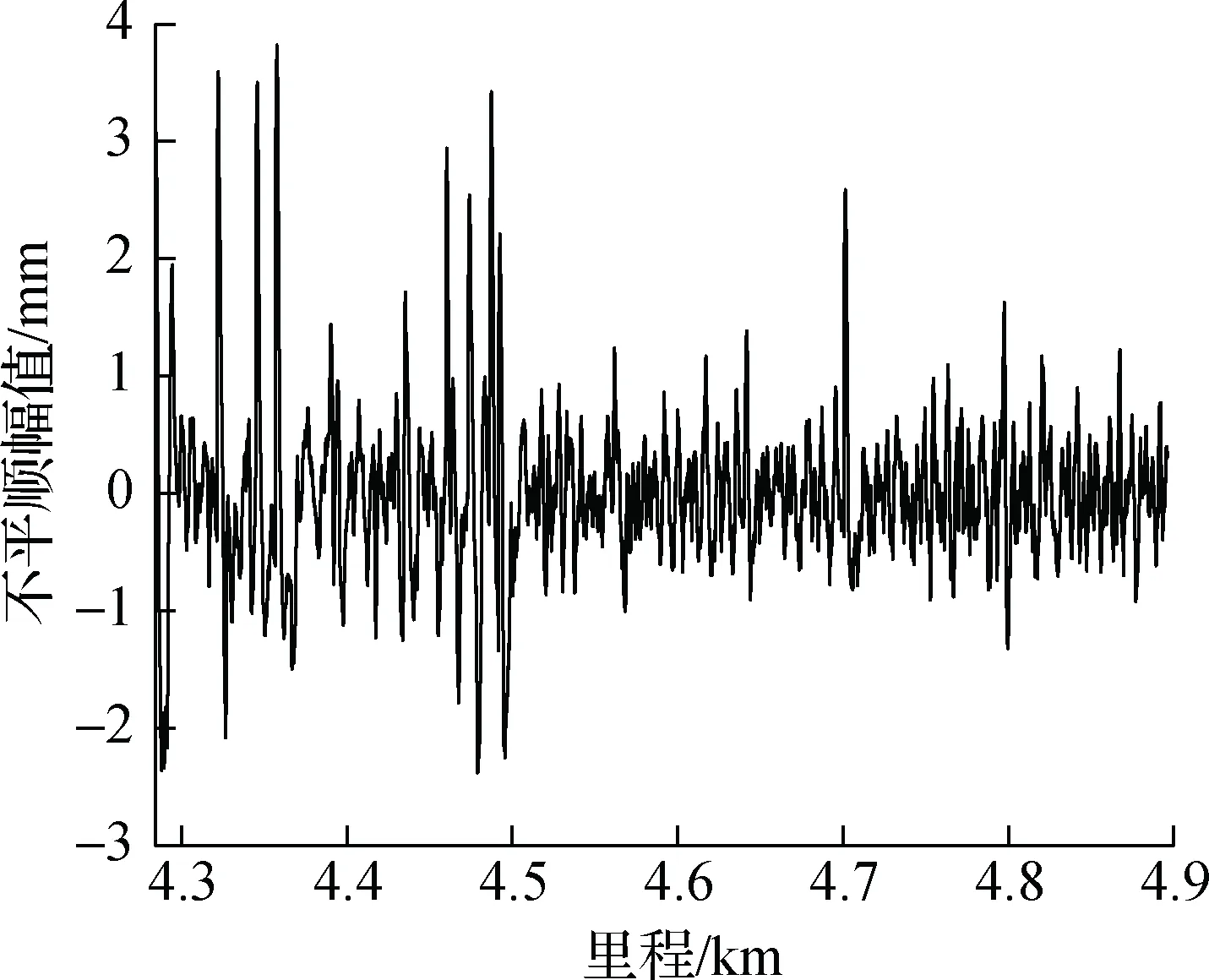
(a) 尖乐区间内轨
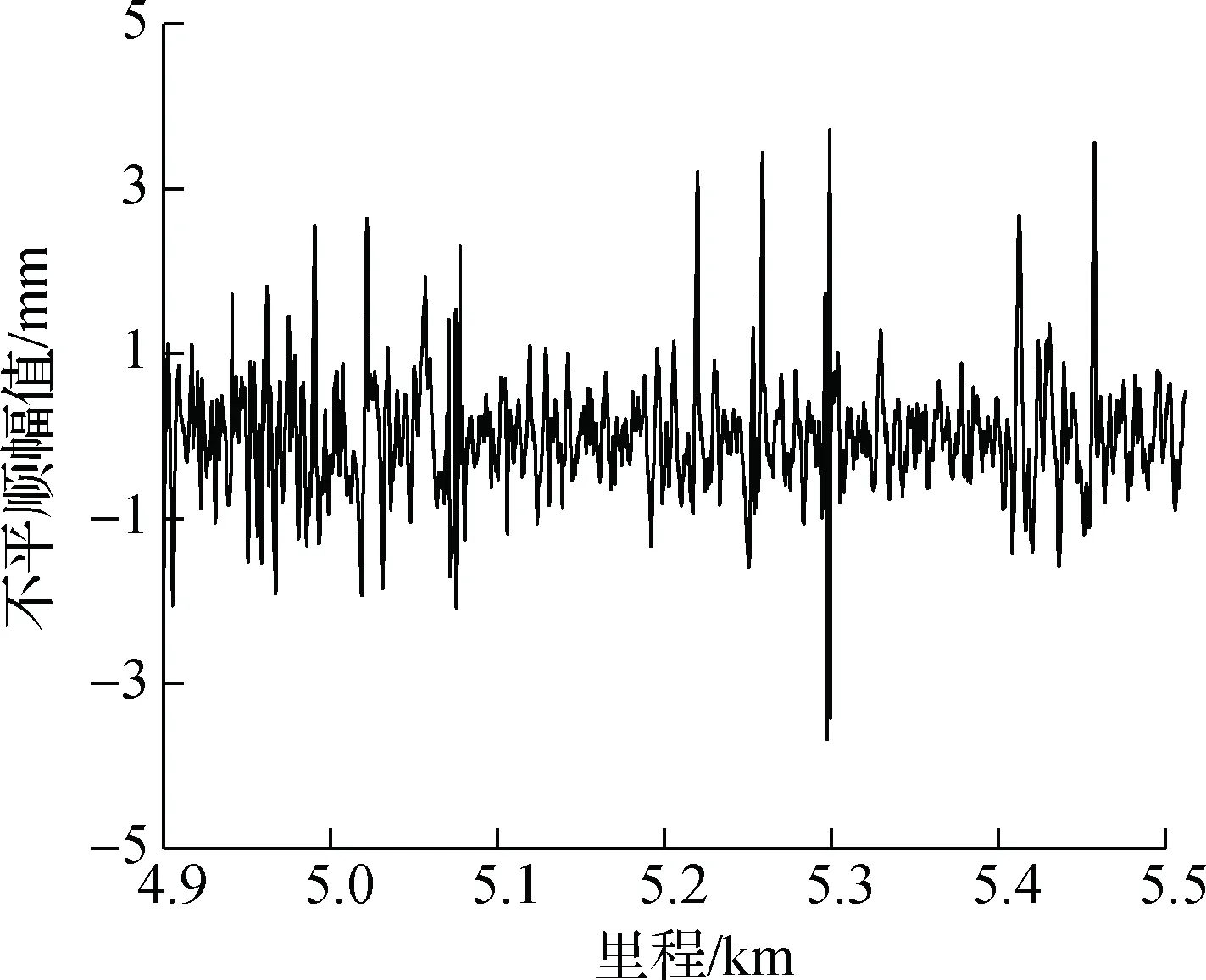
(b) 尖乐区间外轨
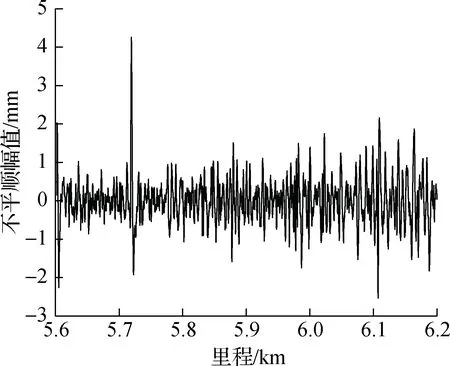
(c) 乐尖区间内轨
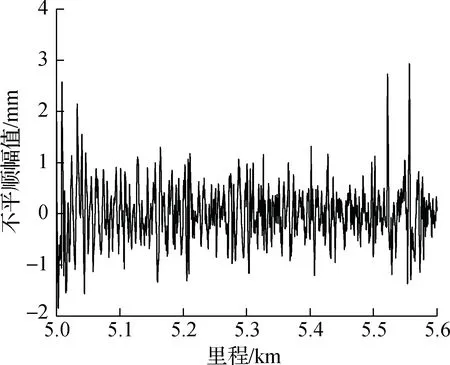
(d) 乐尖区间外轨
通过对钢轨不平顺幅值里程数据进行谱变换,可以得到相应区间的钢轨表面粗糙度级波长谱,如图3所示.图中同时给出了容许的钢轨表面粗糙度级限值曲线[25],在波长谱范围内,特定波长对应的钢轨粗糙度级Lr值在折线以上时,则表示该区间出现了相应波长的钢轨波磨.由图3可得,实测线路区间内轨波磨较为严重,在大于20 mm的波长范围内,钢轨粗糙度级普遍超出限值6 dB以上,且钢轨波磨的主要特征波长为40 mm (见图3(a)和(c),40 mm波长处钢轨粗糙度级超出对应的钢轨粗糙度级限值最多),普遍发生在长枕埋入式整体道床支撑的ZX-2扣件轨道上;外轨波磨较为轻微,仅有个别波长对应的钢轨粗糙度级超出限值,且超出幅度较小,均在3 dB以内.
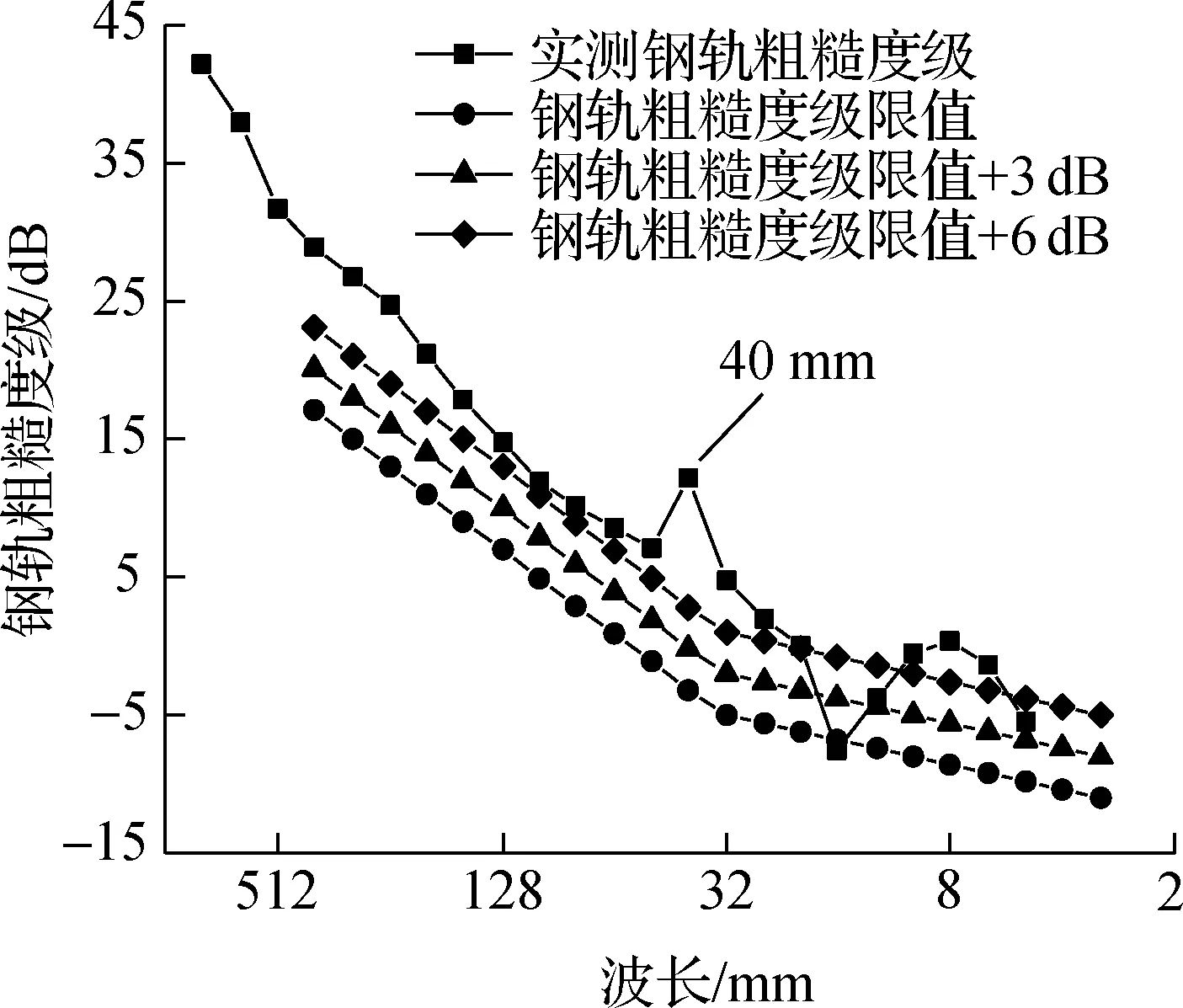
(a) 尖乐区间内轨
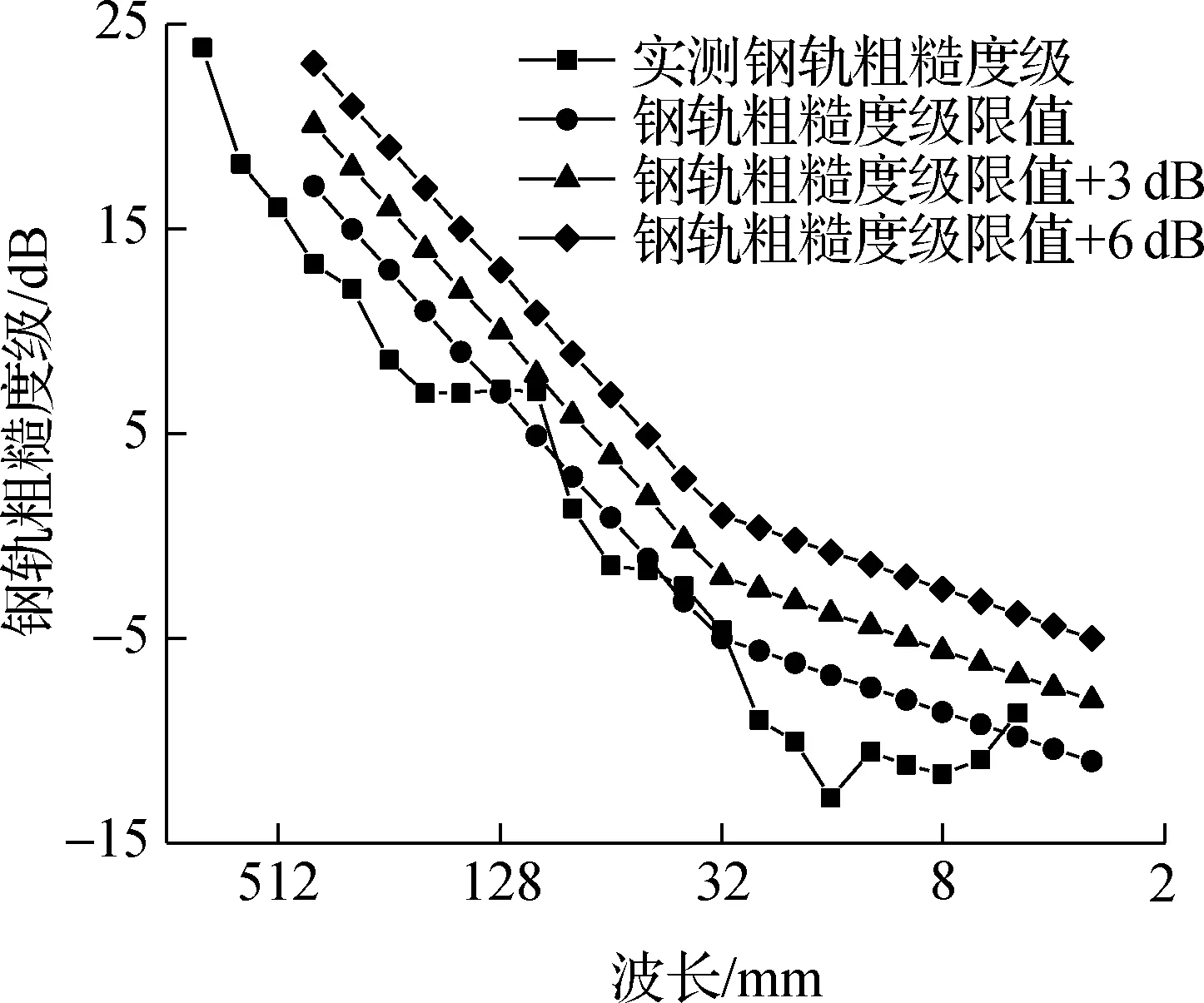
(b) 尖乐区间外轨
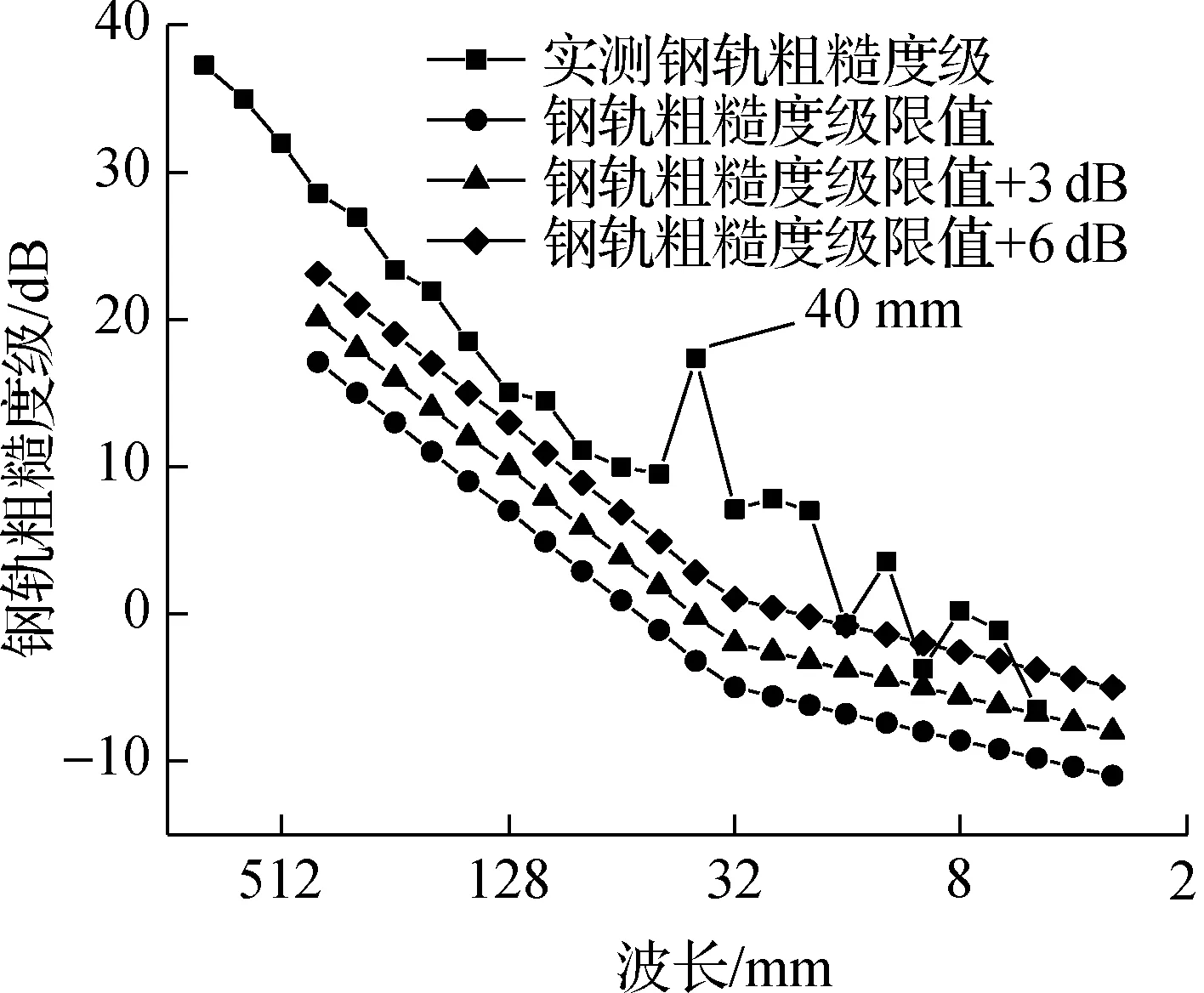
(c) 乐尖区间内轨

(d) 乐尖区间外轨
2 轮轨黏滑特性
利用多体动力学理论,本节首先建立了车辆-轨道刚柔耦合模型;然后,运用现场实测钢轨振动加速度数据,对模型的有效性进行了验证;最后,基于耦合模型,分析了轮轨黏滑特性与钢轨波磨的关系.
2.1 模型建立
车辆-轨道刚柔耦合模型主要包括车辆模型、轨道模型和轮轨接触模型3部分.车辆模型由1个车体、2个转向架和4个轮对组成,其中,车体和转向架均视为刚体,具有纵移、横移、浮沉、侧滚、点头和摇头6个方向的自由度,轮对作柔性化处理,车轮采用LM磨耗型踏面.车体和转向架以及转向架和轮对之间均通过弹簧-阻尼元件进行连接,以模拟二系悬挂和一系悬挂.轨道模型中钢轨采用CHN60轨,ZX-2扣件使用弹簧-阻尼元件进行代替,垂向、横向和纵向刚度分别为40.60、8.79和8.79 MN/m,垂向、横向和纵向阻尼分别为9 900、1 930和1 930 N·s/m,轨下结构参照线路实际情况进行设定.车辆模型和轨道模型的一般性结构参数参考文献[26-28].
轮轨接触采用改进的CONTACT算法,该算法以Duvant-Lions变分原理为依据,将摩擦滚动接触问题转化为变分不等式,从而直接求解由接触斑上作用力和位移乘积表示的最小余能,即[29]
(2)
s.t.PJ3≥0,|PJτ|≤FJ,∀(x,y)∈C
(3)
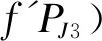

(4)
(5)
式中,vp为质点对流过切平面的平均速度分量;uτ为当前时刻接触质点对的弹性位移差;∂uτ/∂t为质点对切向弹性位移差分量对时间的导数.对稳态滚动接触,∂uτ/∂t=0,则式(5)可写为
(6)
对非稳态滚动接触,∂uτ/∂t≠0.设物体介质由t′→t流过切平面距离的分量为q,则
(7)
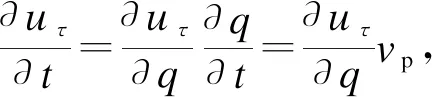
(8)
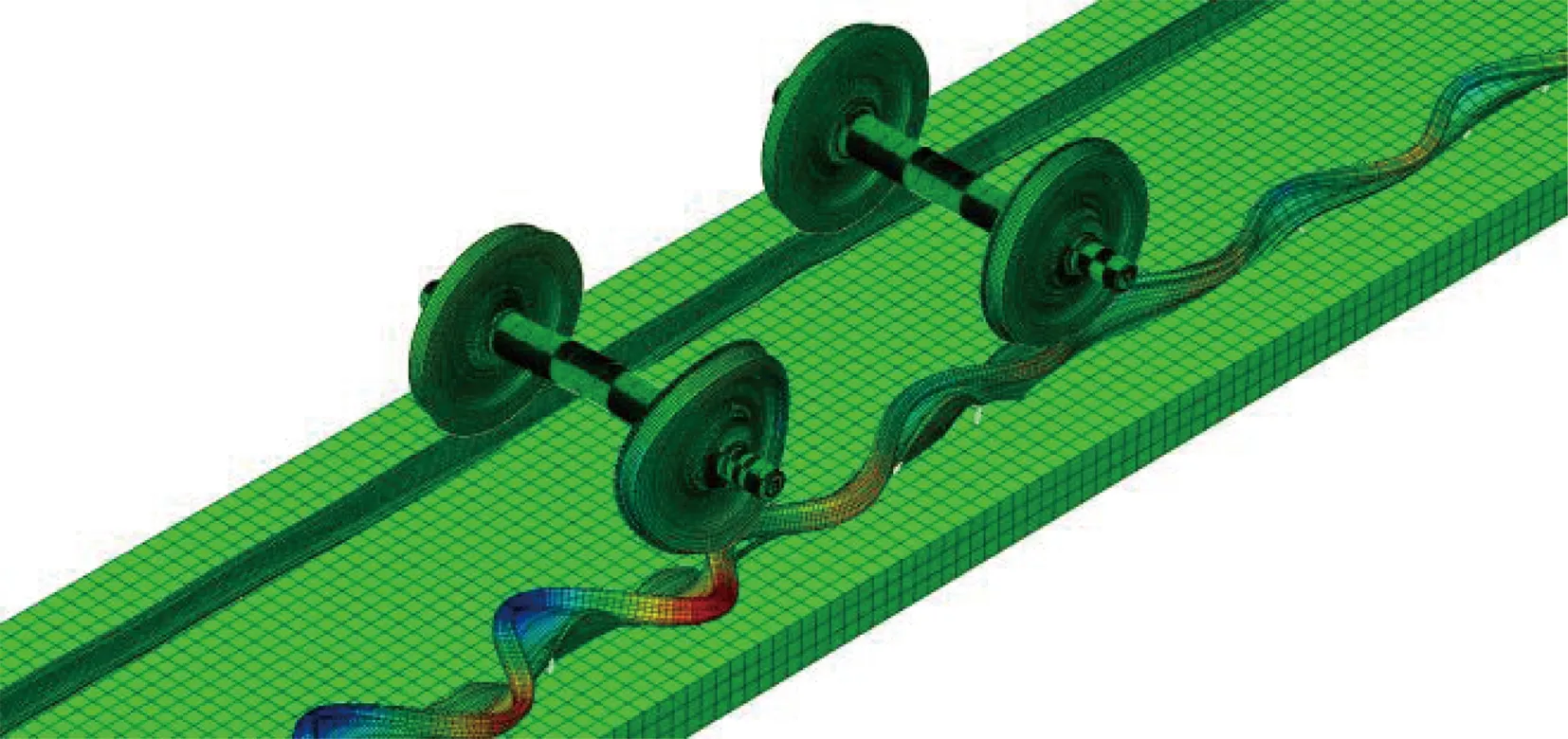
基于车辆模型、轨道模型和轮轨接触模型,构建完成的车辆-轨道刚柔耦合模型,如图4所示.

图4 车辆-轨道刚柔耦合模型示意图
2.2 模型验证
利用线路实测钢轨垂向振动加速度数据,本节对车辆-轨道刚柔耦合模型的有效性进行了验证.参照实测线路,选取区间轨下结构为长枕埋入式整体道床,其他车辆及线路条件同2.1节车辆-轨道耦合模型.首先使用CAT波磨采集仪对实测区间轨面不平顺进行测量,然后将实测轨面不平顺添加至钢轨模型,并进行计算.模型中车辆速度参考实际运营情况取为55 km/h,钢轨测点与实际线路上测点布置位置一致且位于内轨轨底顶面.测点断面钢轨垂向振动加速度的计算与实测时频结果如图5所示,由图可得,计算与实测结果一致性较好,从而验证了模型的有效性.
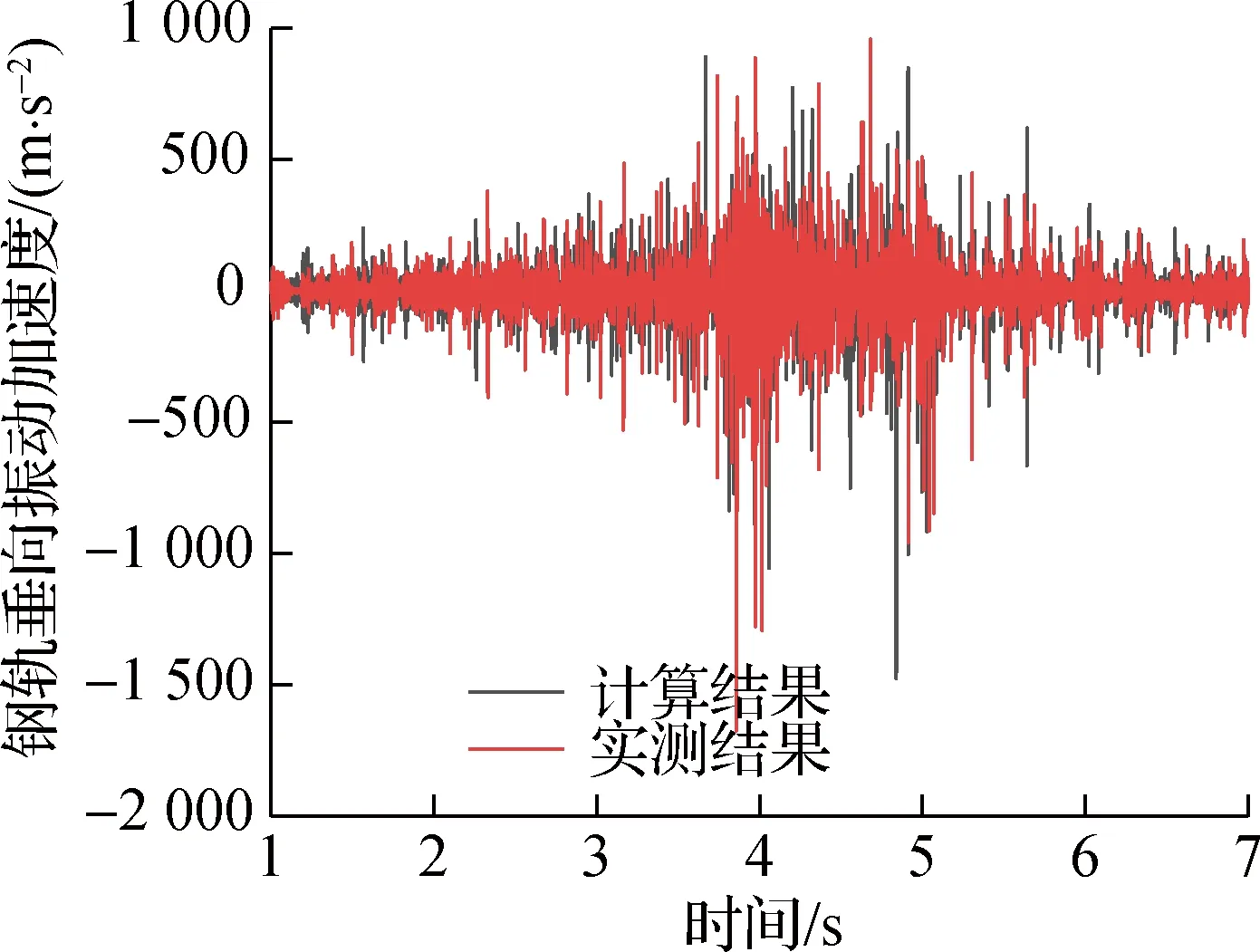
(a) 时域
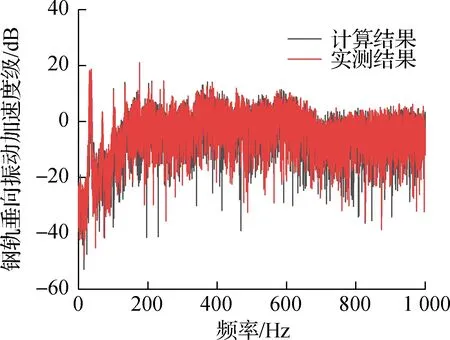
(b) 频域
2.3 轮轨黏滑特性分析
参考实测线路情况,设定模型中线型组成为(50 m直线+100 m缓和曲线+300 m圆曲线+100 m缓和曲线),圆曲线半径为350 m,轨下结构为长枕埋入式整体道床,轨道超高为80 mm,轨距为1 435 mm,轮轨静摩擦系数为0.3,车辆在圆曲线上的运行速度为55 km/h.由于本文目的是探究钢轨波磨的形成原因,因此不考虑轨面不平顺的影响,即钢轨表面是光滑的.通过数值计算,可以获得车辆在圆曲线上运行时的纵、横向蠕滑力/率,轮轨法向力等参量,同时将轮轨蠕滑力与法向力作比可以得到轮轨界面黏着系数,即
(9)
式中,μ1和μ2为纵向和横向黏着系数;F1和F2为纵向和横向蠕滑力;P3为法向力.本文主要通过分析轮轨黏着系数与蠕滑率的关系,研究小半径曲线钢轨波磨的形成原因,其中纵向和横向蠕滑率定义式为
(10)

由于车辆曲线通过时,导向轮对和从动轮对的运动形态和受力情况不同,因此,本节选取单节车辆前转向架的2个轮对(即导向轮对和从动轮对)进行分析,相应的轮轨黏滑特性曲线如图6和图7所示.
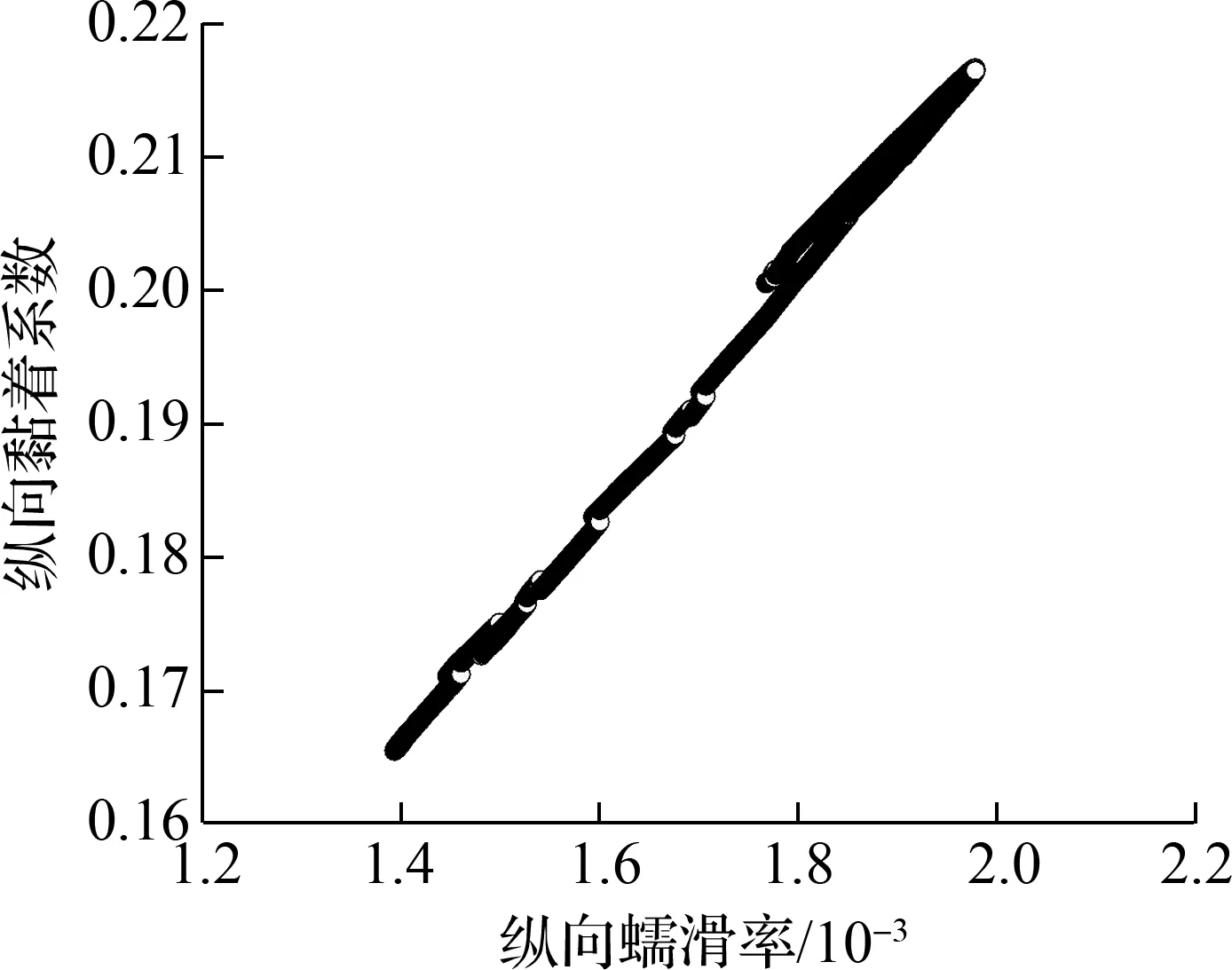
由图6可知,随着横向蠕滑率的增加,导向轮对内轮-内轨的横向黏着系数逐渐减小,轮轨黏滑曲线出现了负斜率段,即随着内轮-内轨横向速度差的增大,轮轨界面的黏着系数反而下降,这说明内轮-内轨发生了横向的相对滑移.轮轨横向黏着-滑移状态的转变会导致轮轨产生横向黏滑扭振[30],而且这种状态的转变循环往复,以实现车辆顺利通过曲线.当内轮-内轨黏着时,钢轨磨耗小;当内轮-内轨滑动时,钢轨磨耗大,因而随着车辆运行次数的增加,内轨轨面最终形成了波浪形磨耗.其余轮轨界面的黏着系数均与对应的蠕滑率成正相关,未出现明显负斜率段,说明对应的轮轨界面不会发生微观滑移,从而不容易产生钢轨波磨.
根据图7,可以发现从动轮对外轮-外轨的横向黏滑曲线出现了负斜率现象,其余轮轨黏滑曲线未见明显负斜率区间,表明从动轮对的外轮-外轨也会产生横向黏滑扭振,从而引发外轨形成波磨.但是,从动轮对外轮-外轨发生横向黏滑扭振所需的黏着系数0.070大于导向轮对内轮-内轨发生横向黏滑扭振所需的黏着系数0.017,因此相对而言,从动轮对外轮-外轨的横向黏滑扭振强度较弱且不易发生,即外轨波磨较为轻微或不易形成.如果考虑钢轨表面不平顺等不利工况时,则可能会促使从动轮对外轮-外轨发生较强的横向黏滑扭振,进而导致外轨产生明显波磨.

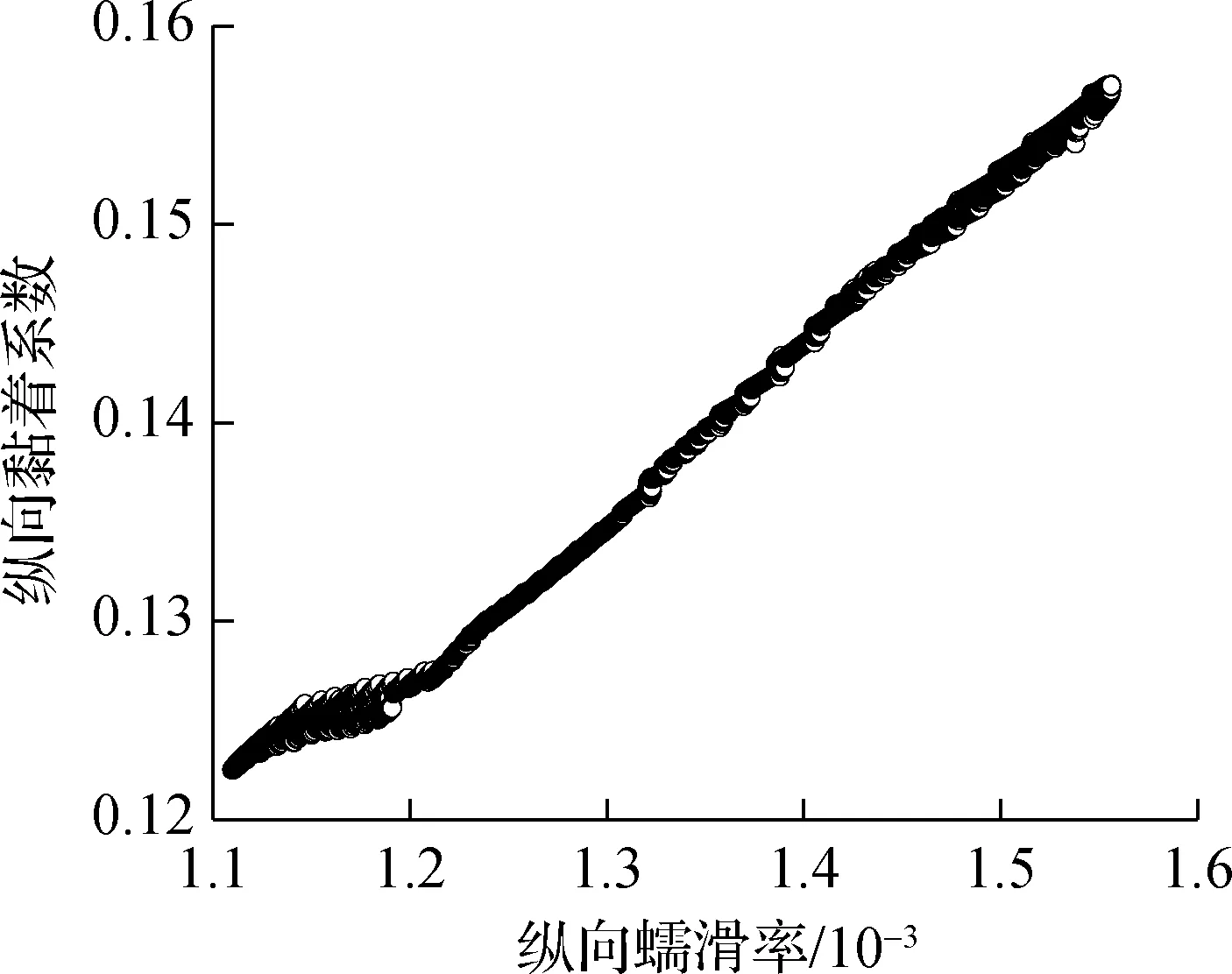
(a) 内轮-内轨纵向黏滑曲线
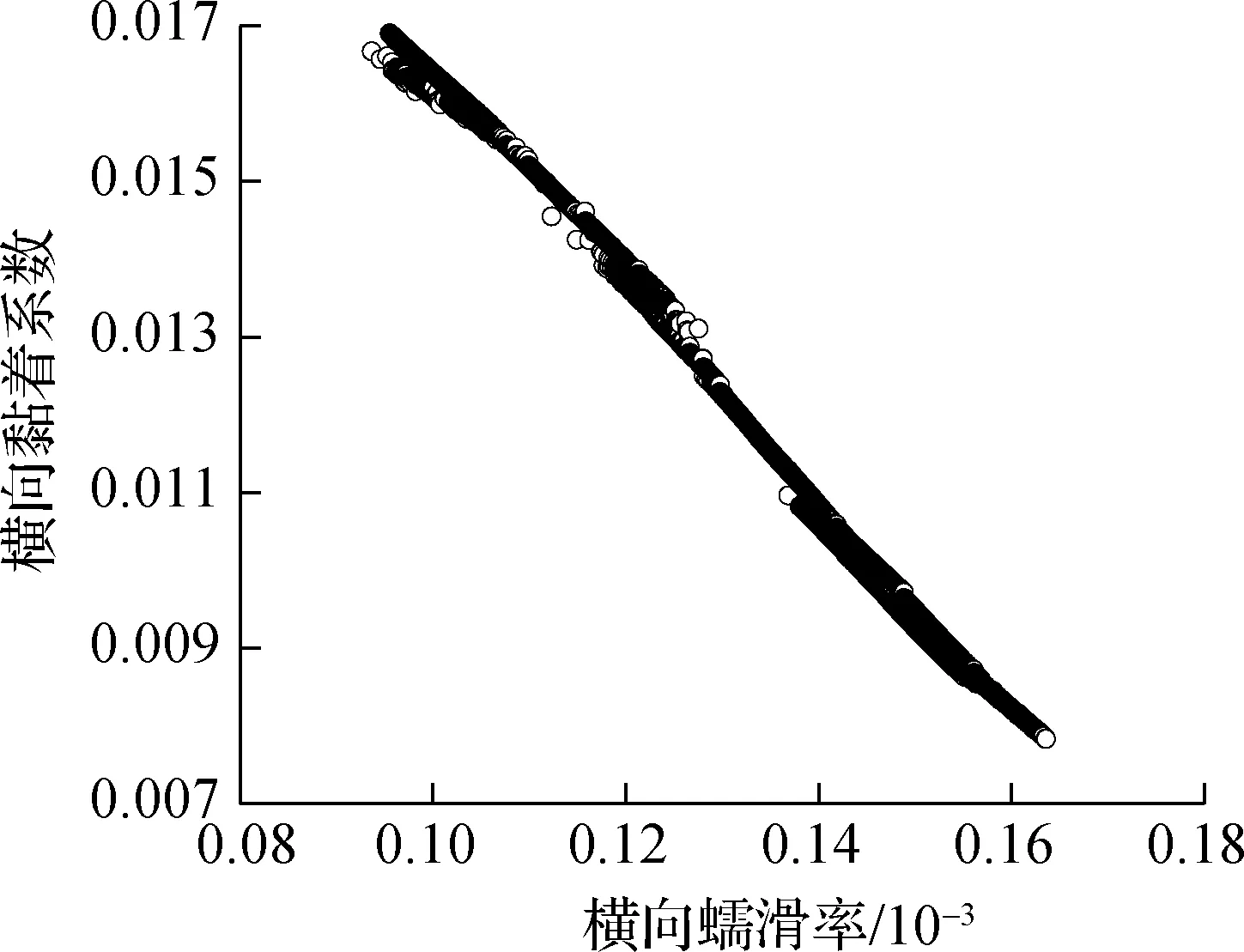
(b) 内轮-内轨横向黏滑曲线
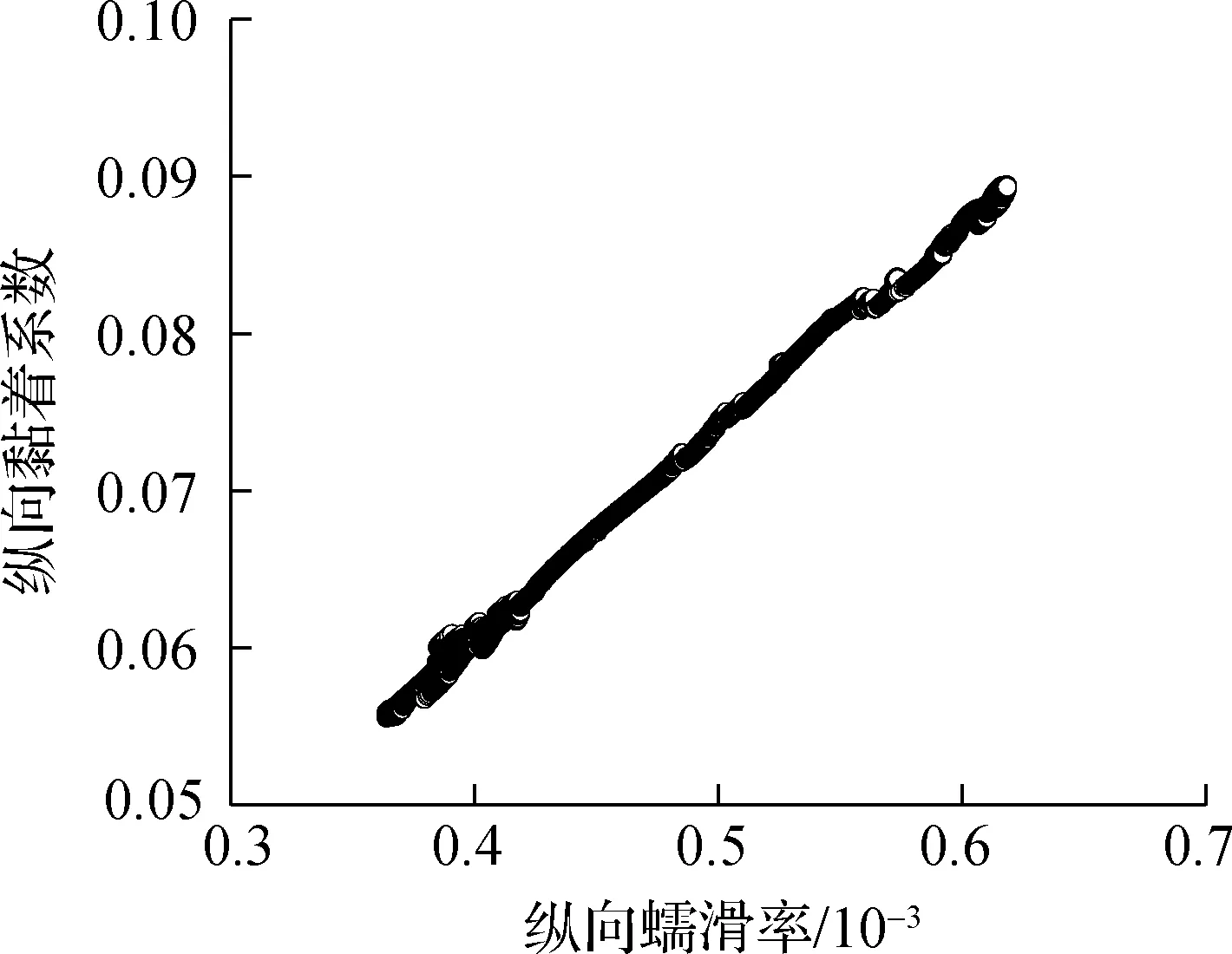
(c) 外轮-外轨纵向黏滑曲线
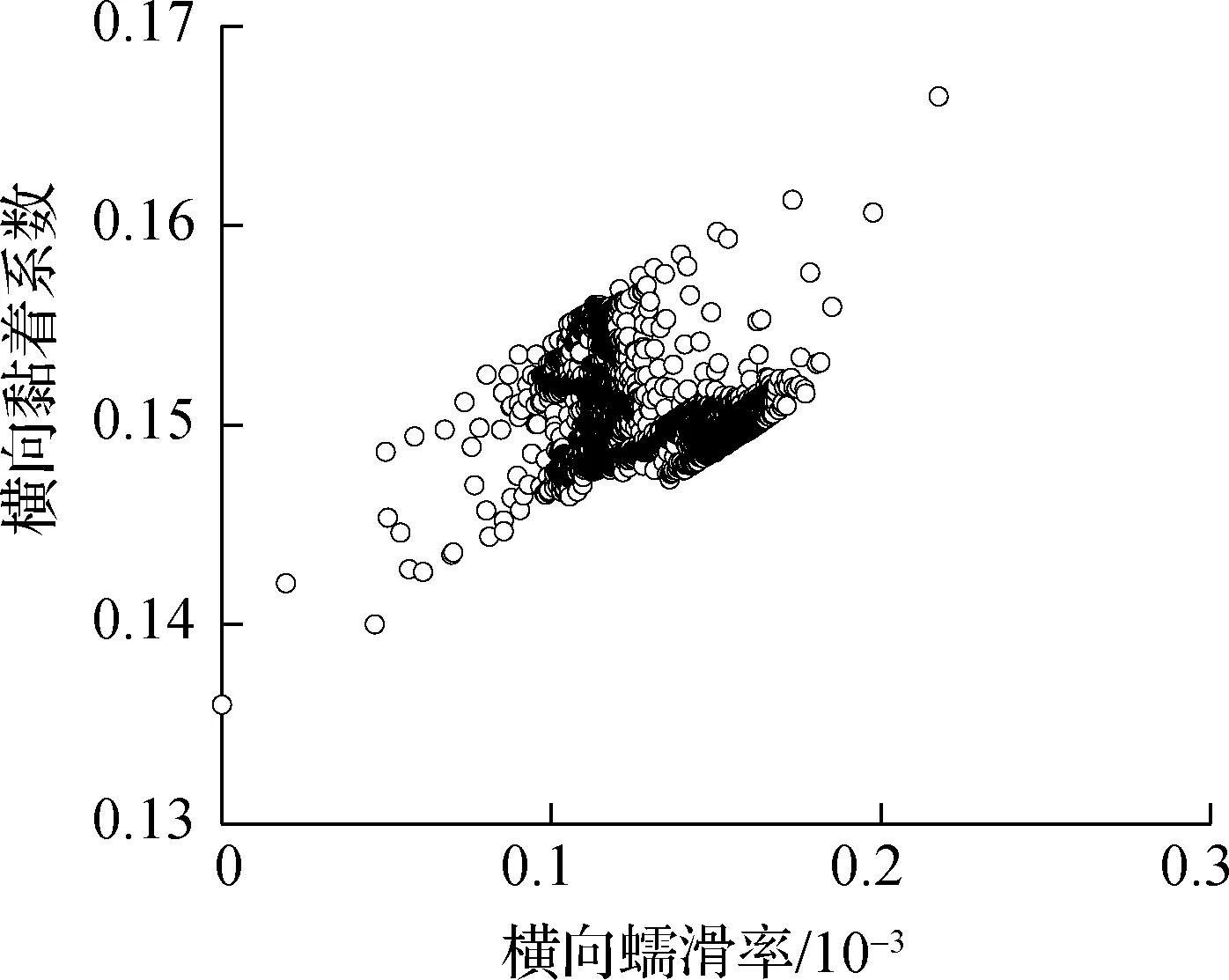
(d) 外轮-外轨横向黏滑曲线
(a) 内轮-内轨纵向黏滑曲线

(b) 内轮-内轨横向黏滑曲线
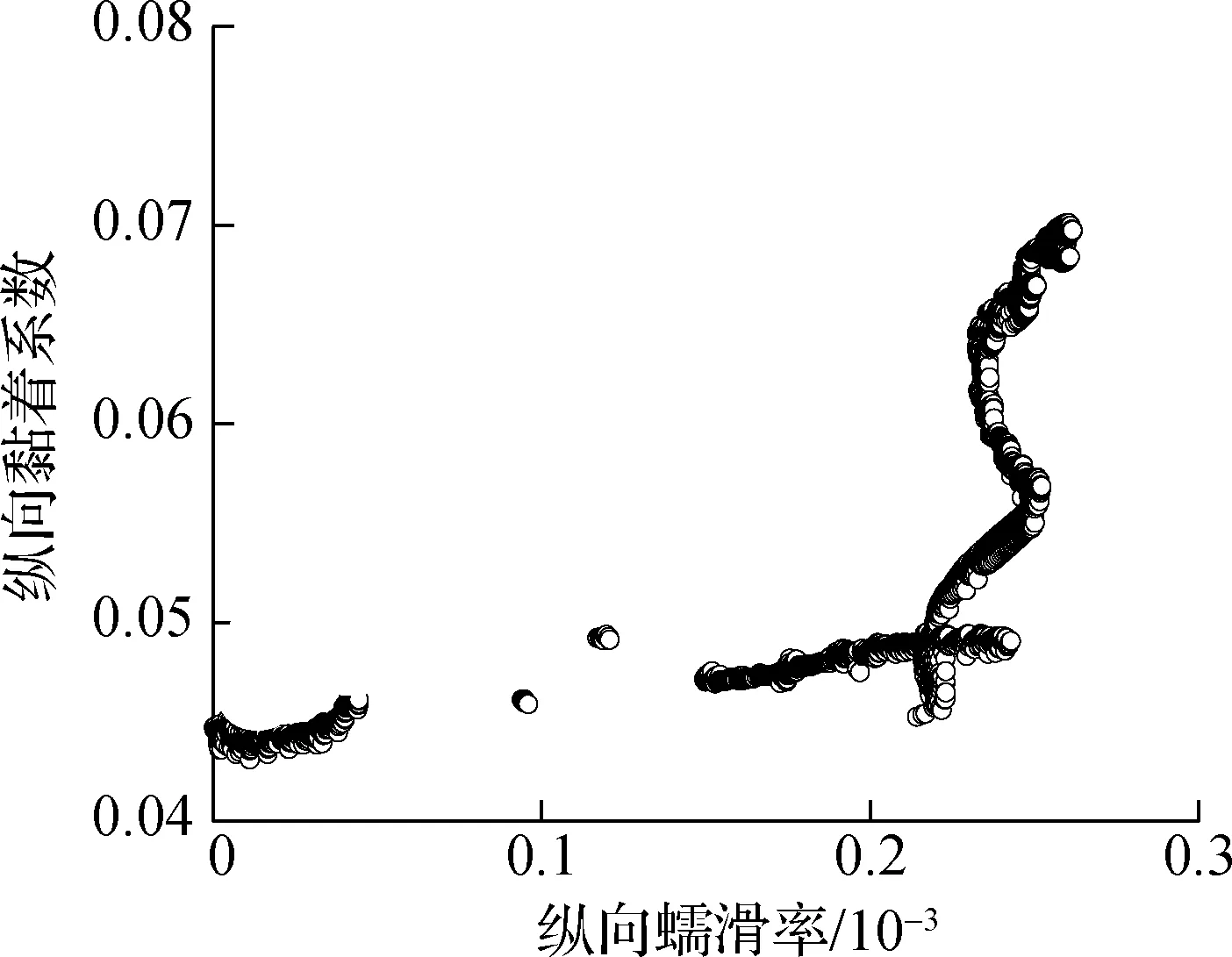
(c) 外轮-外轨纵向黏滑曲线
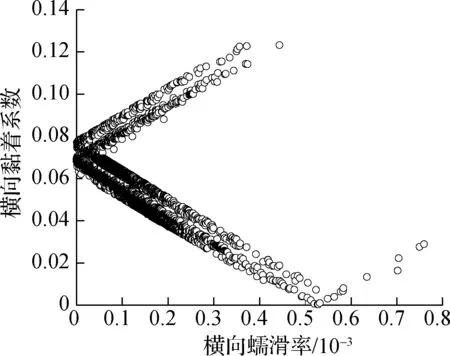
(d) 外轮-外轨横向黏滑曲线
此外,图6(d)或图7(d)的曲线与其他3幅图曲线的规律有所不同,在确定的蠕滑率位置处呈现较大的波动范围,这与小半径曲线轨道外轮与外轨在横向上发生频繁的侧面接触有关.
为探究图6(b)和图7(d)所表示的轮轨黏滑扭振的振动频率特性,将对应的黏着系数进行频谱变换,可得黏着系数振动等级频谱图,如图8所示.由图可得,导向轮对内轮-内轨横向黏着系数频谱曲线中出现了380~385 Hz的特征频率,而从动轮对外轮-外轨横向黏着系数频谱曲线则未表现出明显的特征频率,且黏着系数振动等级(均小于 -120 dB)相对导向轮对内轮-内轨横向黏着系数振动等级(绝大部分大于-120 dB)较小,这说明导向轮对内轮-内轨的横向黏滑扭振强度更大,更容易诱发波磨生成且波磨程度较为严重.同时,由1.2节可知实测线路上钢轨波磨的主要特征波长为40 mm,实测区间车辆运行速度约为55 km/h,因此,根据频率计算公式,可得钢轨波磨的主要特征频率为382 Hz,而图8(a)显示的导向轮对内轮-内轨横向黏着系数频谱曲线的特征频率范围380~385 Hz与其接近,这证实了实测区间的内轨波磨是由导向轮对内轮-内轨的横向黏滑扭振所致.频率计算公式可写为
(11)
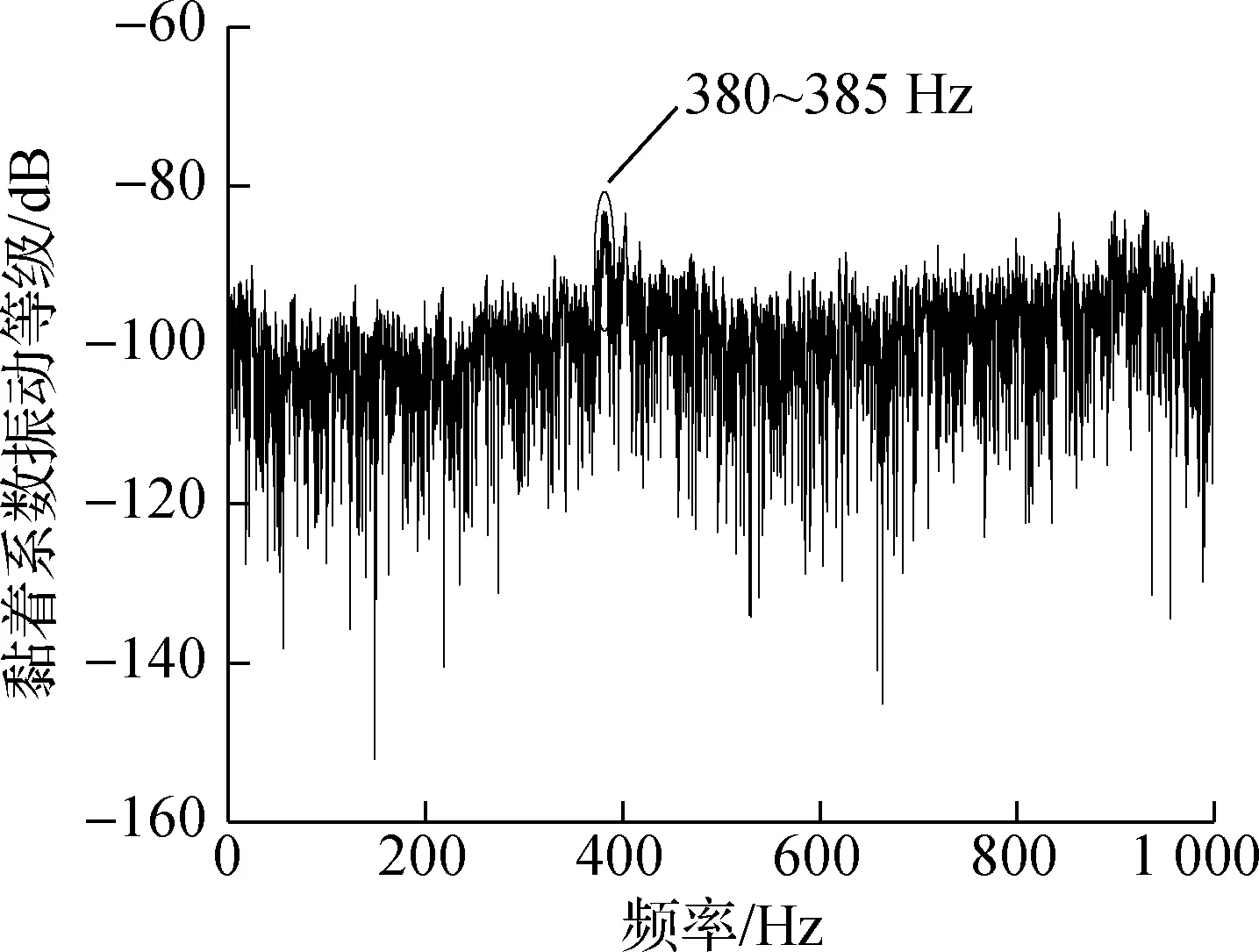
(a) 导向轮对内轮-内轨横向黏着系数

(b) 从动轮对外轮-外轨横向黏着系数
式中,ω为波磨频率,Hz;v为车辆运行速度,km/h;λ为波磨波长,mm.
上述分析显示,导向轮对内轮-内轨的横向黏滑扭振导致了内轨波磨的产生,从动轮对外轮-外轨也有发生横向黏滑扭振的可能性,但是强度较弱且概率较低,因此,在小半径曲线上,内轨波磨较为严重,外轨波磨整体相对轻微或部分区间不存在波磨现象,这与线路实测情况相符.以下将从轮轨系统模态振型的角度考量,进一步探讨轮轨系统的振动特性对钢轨波磨的影响.
3 轮轨振动特性
运用有限元软件ABAQUS,建立了多轮对-轨道三维实体模型,其中轮对考虑导向轮对和从动轮对2个轮对,轨道包括钢轨、扣件、道床板以及接地弹簧.钢轨和道床板两端面为固定约束,钢轨通过扣件(弹簧-阻尼元件)与道床板连接,道床板通过接地弹簧与基础连接,模型示意图如图9所示.该模型中车轮名义滚动圆半径为420 mm,踏面类型为LM磨耗型,钢轨采用CHN60轨,轮轨摩擦系数设为0.3,轨距为1 435 mm,轨道中心线长度为36 m,对应曲线半径为350 m,轨道超高为80 mm.轮轨法向接触采用硬接触,切向接触采用罚函数法.轮对-轨道系统的结构参数取值与动力学模型一致.
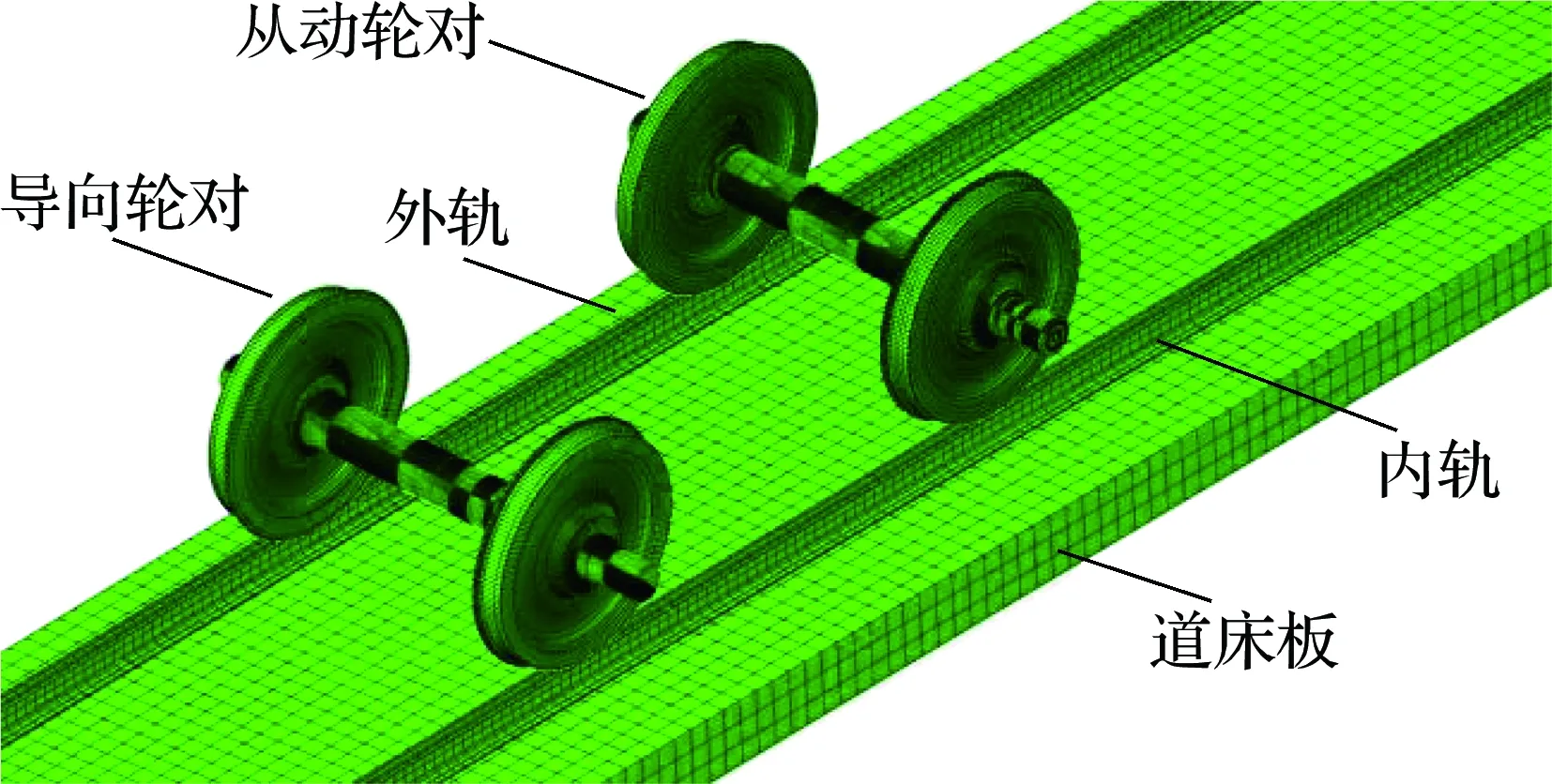
图9 多轮对-轨道有限元模型
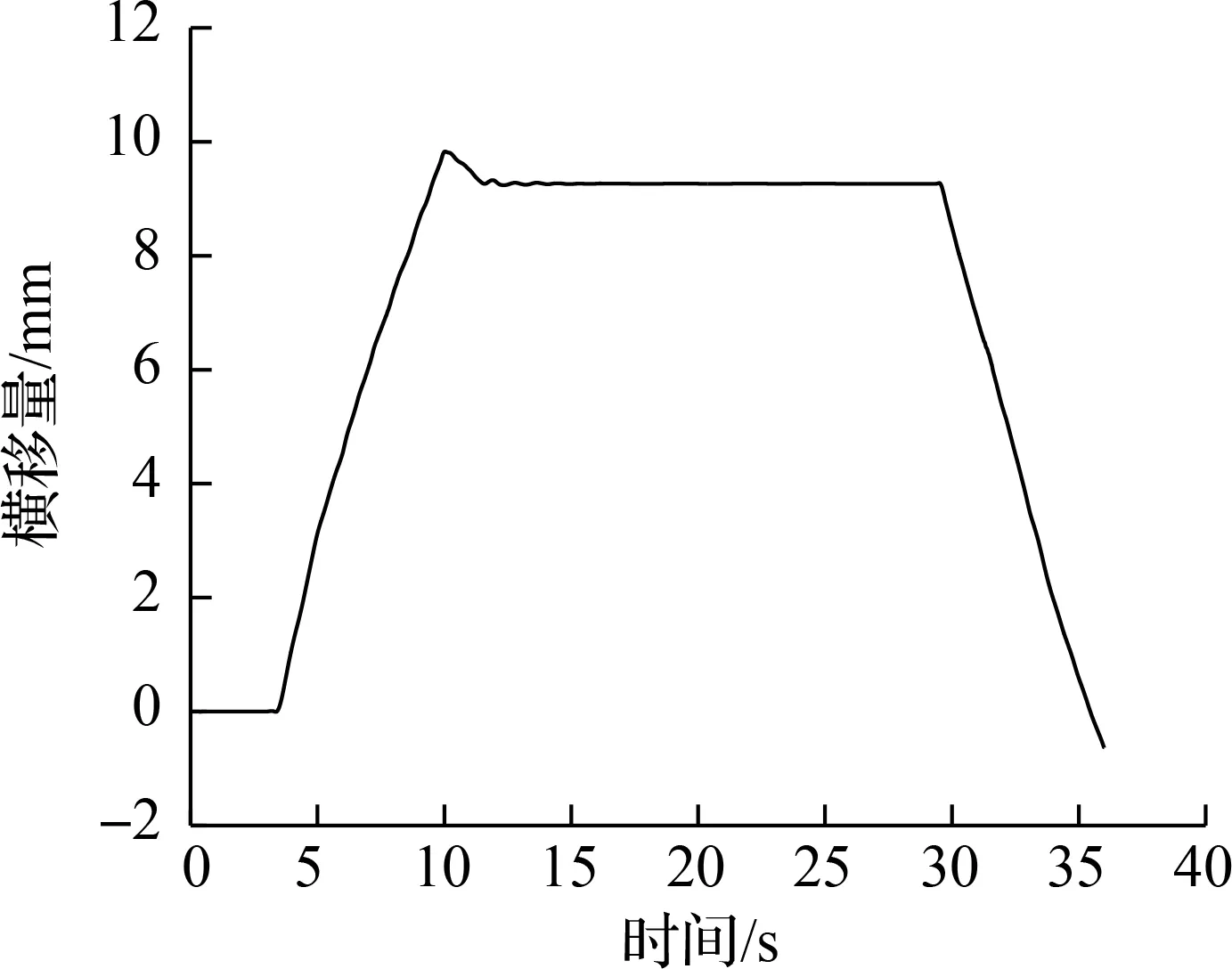
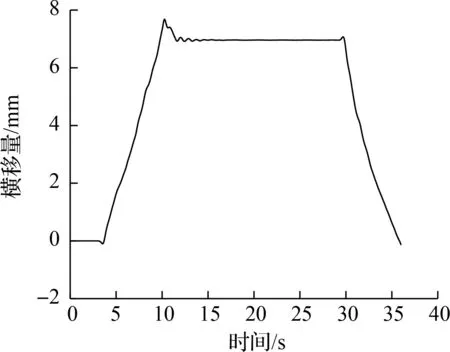
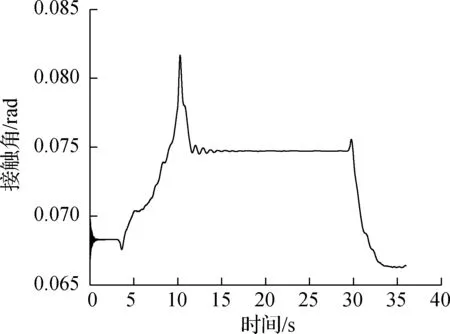
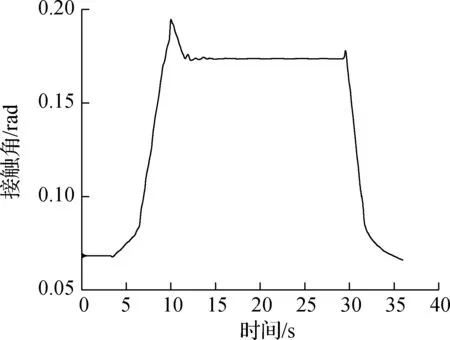
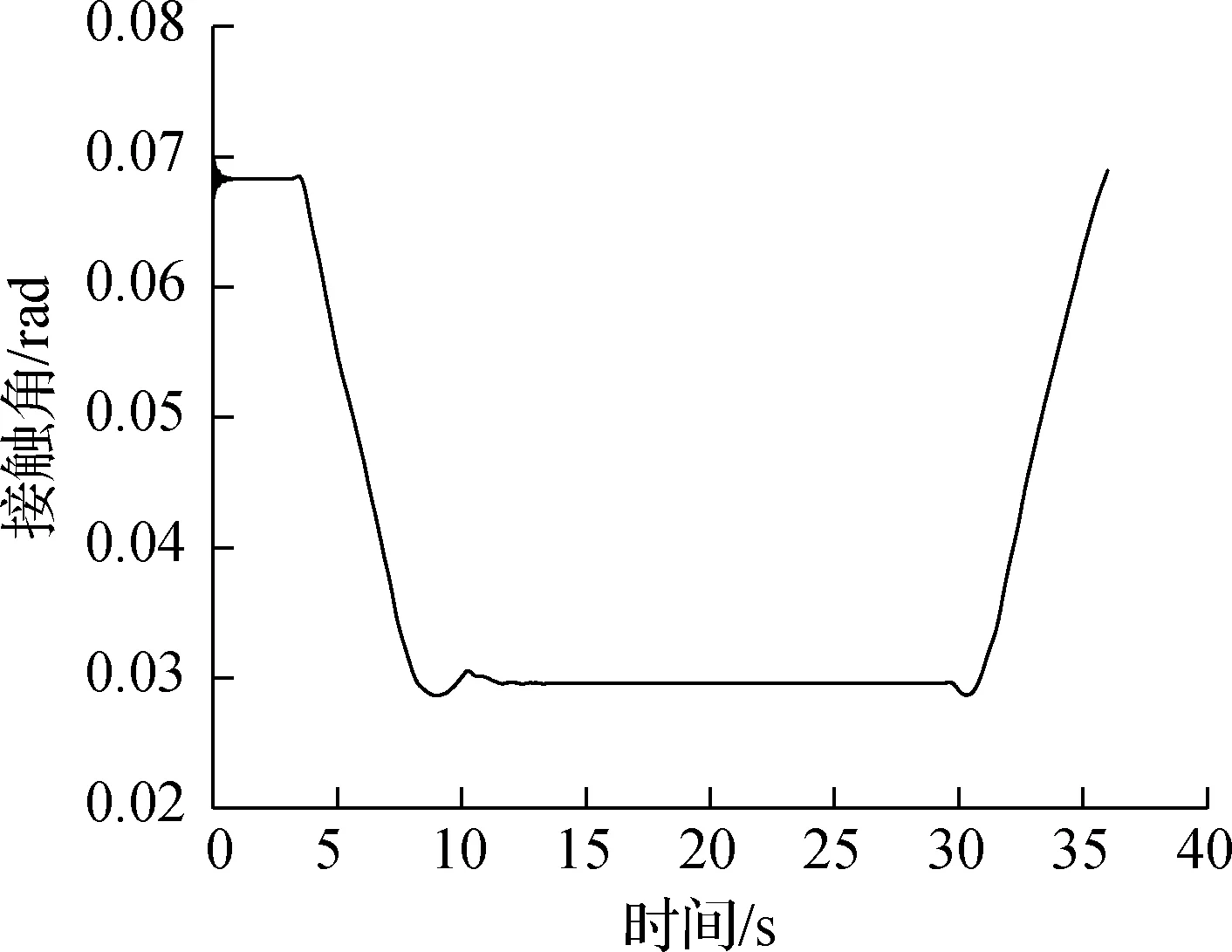
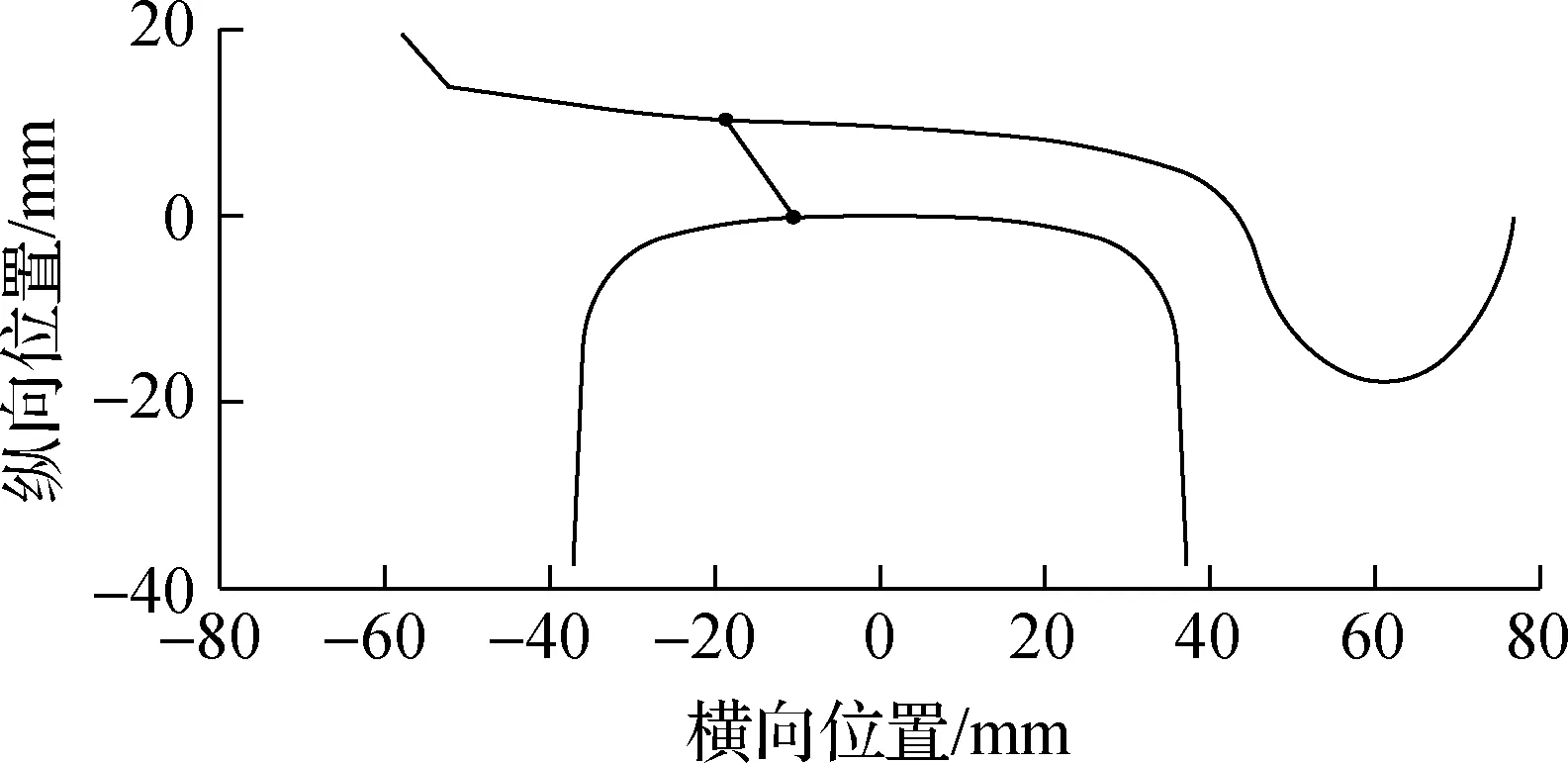
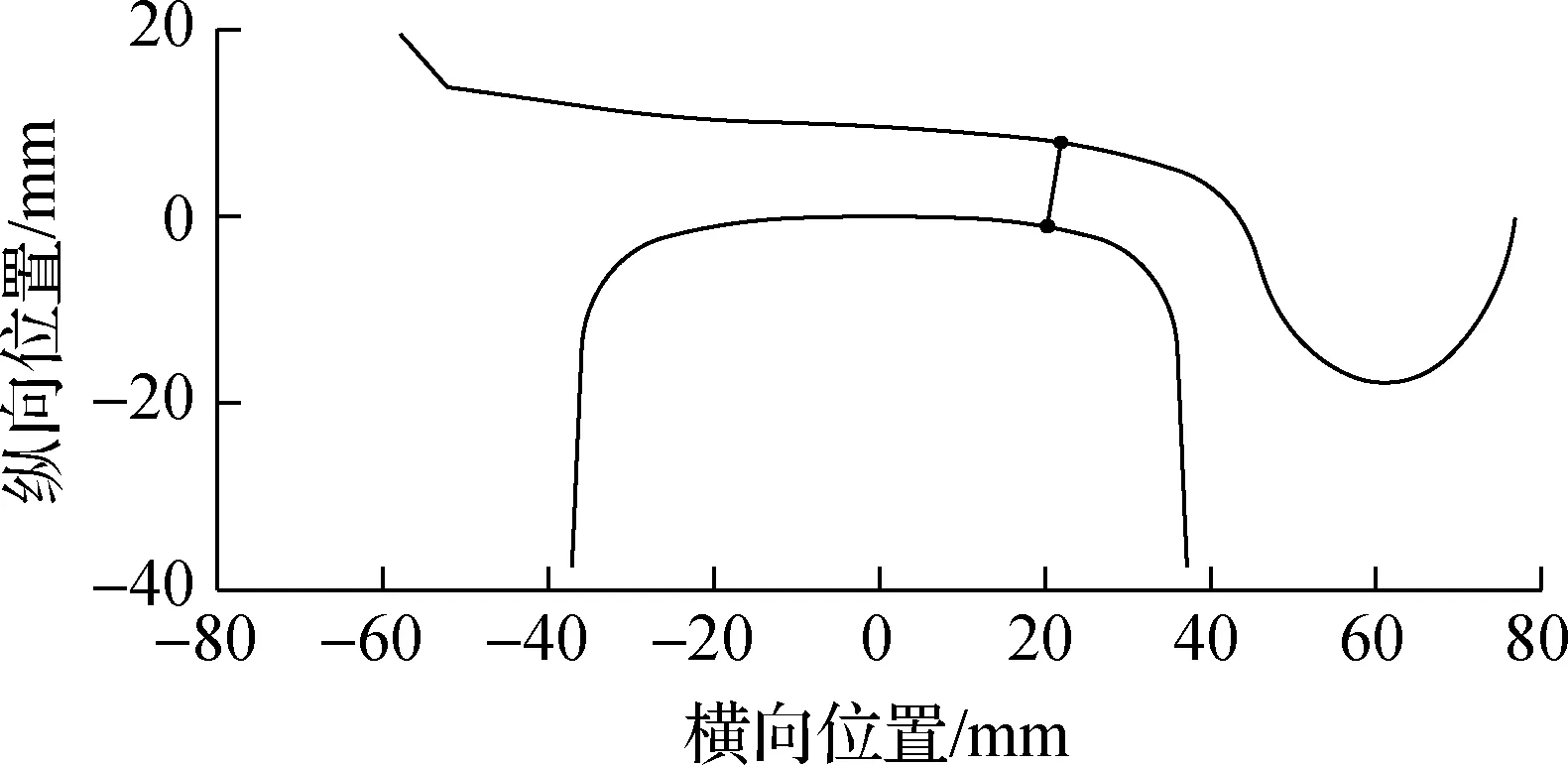
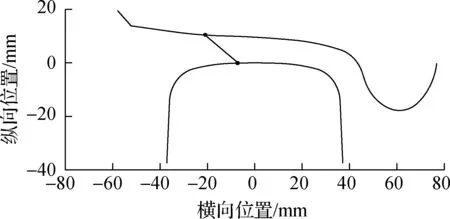
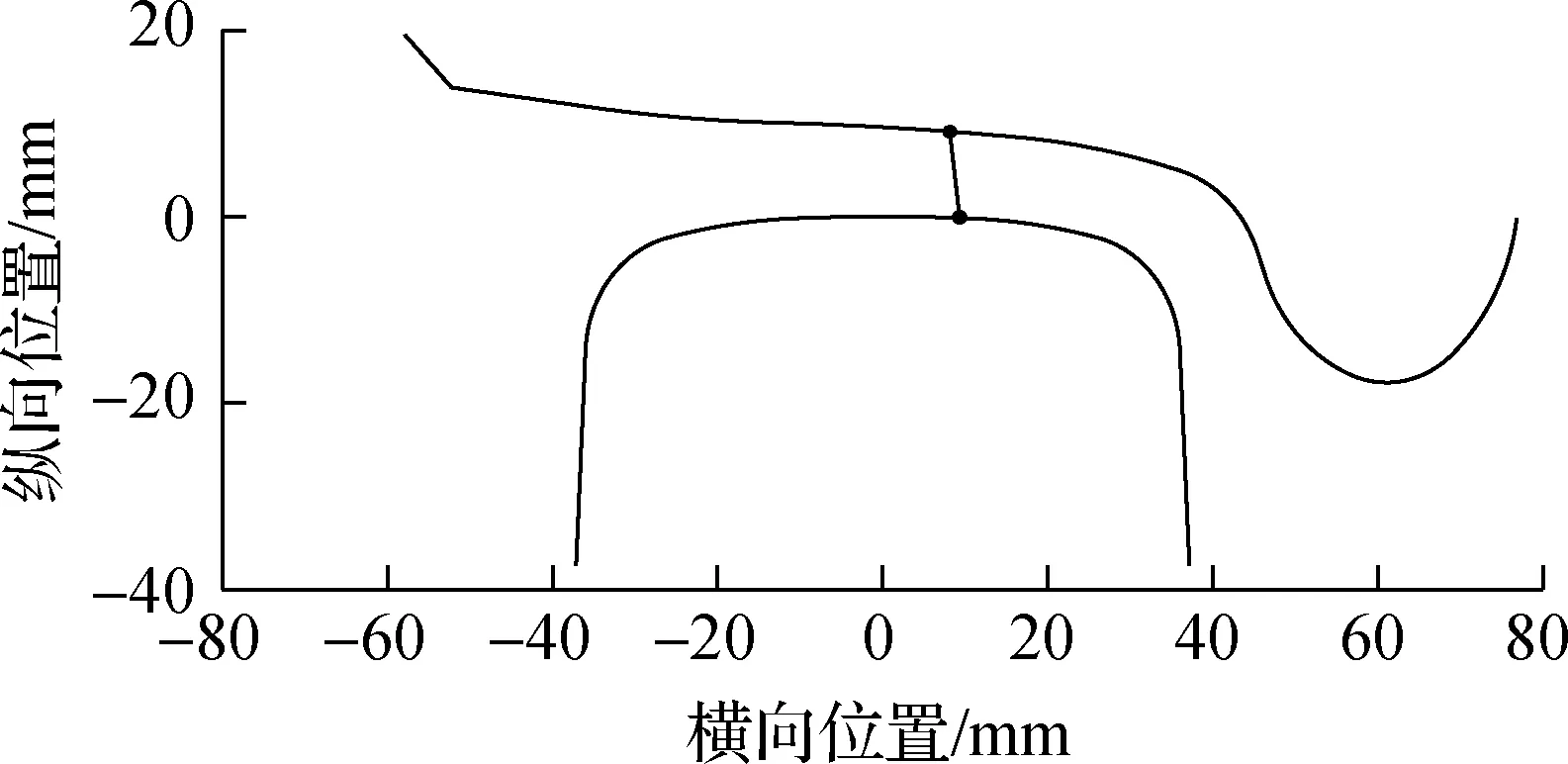
有限元模型中导向轮对和从动轮对在钢轨上的位置主要依据轮对横移量和轮轨接触角确定,其中轮对横移量和轮轨接触角由动力学模型计算得到,如图10和图11所示,最终确定的轮轨接触点对如图12所示.
为研究轮轨系统的振动特性与钢轨波磨的关系,本节对上述建立的多轮对-轨道三维有限元模型进行了模态分析.分析结果中与实测波磨主要特征频率382 Hz相近的频率为388 Hz,对应振型如图13(a)所示.由图13(a)可以看出,在与钢轨波磨主要特征频率相近频率处,导向轮对内轮与内轨发生了显著的横向扭转振动,而其他轮轨位置未见明显振动,这表明导向轮对内轮-内轨的横向扭转振动最终导致了内轨波磨的出现.
(a) 导向轮对
(b) 从动轮对
进一步对建立的有限元模型展开复模态分析,即轮轨系统的摩擦自激振动分析,以研究其与轮轨系统黏滑负斜率特性之间的关系.参考摩擦自激振动相关理论[31-33],保持有限元模型参数不变,进行复特征值分析,并提取复特征值实部aj取最大值时的模态振型,绘制于图13(b).由图13(b)可以看出,该模态振型与图13(a)相似,其对应频率384 Hz与图13(a)模态振型对应频率388 Hz相近,且与实测波磨主要特征频率382 Hz更为接近.同时,该振型对应的复特征值实部aj大于0,由于复特征值实部aj大于0表示系统处于不稳定状态,进而会导致轮轨系统产生摩擦自激振动并诱发钢轨波磨的形成,因此从轮轨系统的摩擦自激振动角度,本节再次说明了内轨波磨的产生原因是导向轮对内轮-内轨的横向扭转不稳定振动造成的,这与黏滑负斜率特性分析所得结论相符.
根据以上分析可得,导向轮对内轮-内轨的黏滑负斜率现象促使了对应接触界面的轮轨横向扭转振动,所以轮轨黏滑负斜率特性对于钢轨波磨的形成至关重要.下面将对轮轨黏滑负斜率现象的形成机制展开进一步研究.此外,轮轨摩擦系数的取值确定了促使黏滑扭振发生的黏着系数的上限,即随着轮轨摩擦系数的增加,能够促使黏滑扭振发生的黏着系数的上限也会随之增加,从而使得诱发波磨发生的特定方向上的黏滑扭振更容易出现,这与轮轨系统摩擦自激振动理论中摩擦系数越大,系统越不稳定一致[31].
(a) 导向轮对内侧
(b) 导向轮对外侧
(c) 从动轮对内侧

(d) 从动轮对外侧
(a) 导向轮对内侧
(b) 导向轮对外侧
(c) 从动轮对内侧
(d) 从动轮对外侧

(a) 频率388 Hz下轮对-轨道系统模态振型
(b) 频率384 Hz下轮对-轨道系统复模态振型 (f=384 Hz, aj=12.324)
4 轮轨黏滑负斜率形成机制
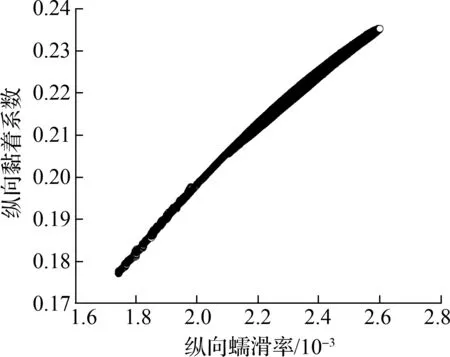
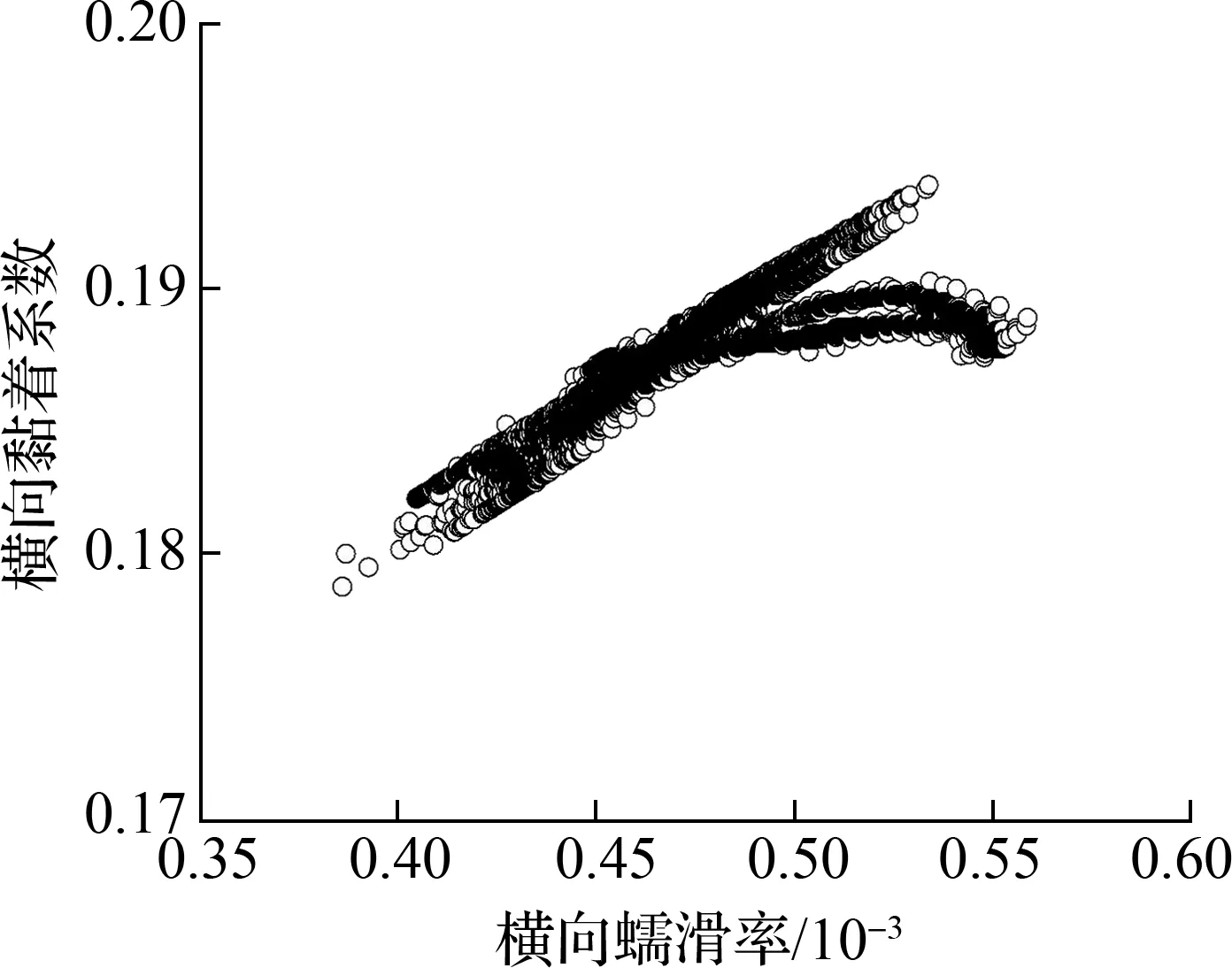
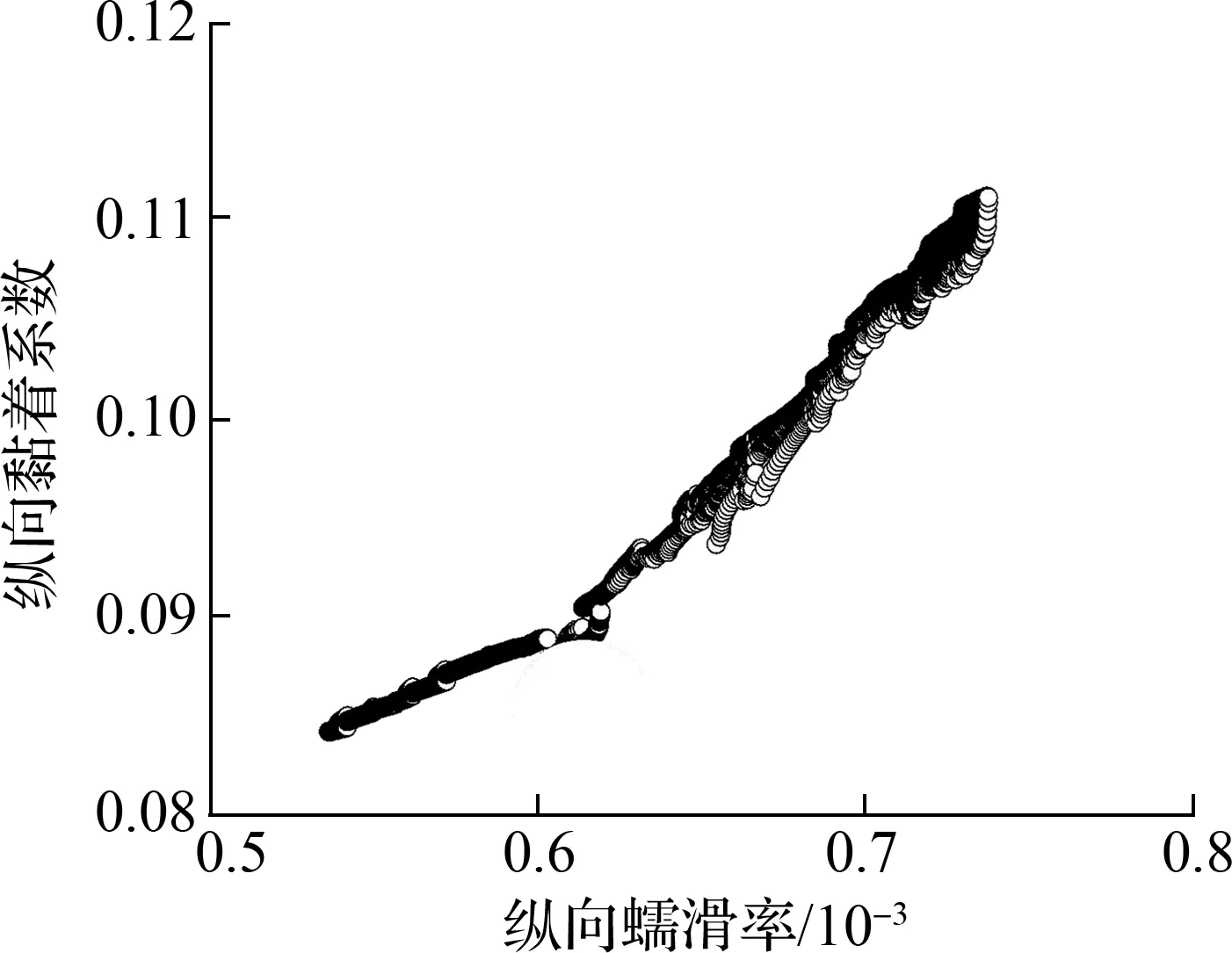
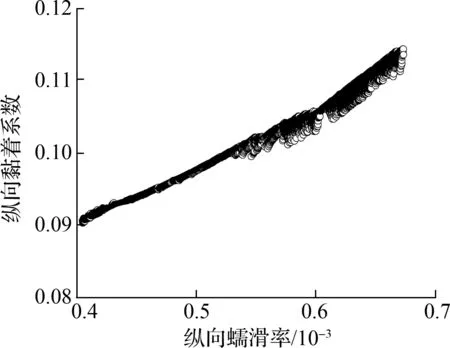
轮轨黏滑曲线与轮轨蠕滑力/率及法向力有关,所以内外侧轮轨蠕滑力/率及法向力的分配对内外侧轮轨的黏滑特性具有重要的影响,而轨道超高可能是决定蠕滑力/率及法向力分配的关键因素之一,因此本节将主要分析轨道超高对轮轨黏滑负斜率形成机制的作用.参考图14(图中S1为两股钢轨轨头中心间距离),并按照轨道平衡超高计算公式,当行车速度为55 km/h、线路曲线半径为350 m时,可得平衡超高值约为100 mm (取5 mm的倍数).基于此,下面将分别分析轨道欠超高20 mm(轨道超高值80 mm,对应实际线路工况)、轨道平衡超高(轨道超高值100 mm)和轨道过超高20 mm(轨道超高值120 mm)3种工况,相应的轮轨黏滑特性曲线如图6、图7、图15~图18所示.轨道平衡超高计算公式可写为
(12)
式中,he为平衡超高值,mm;Rc为线路曲线半径,m.

图14 轨道超高状态示意图
根据图15和图16可得,当轨道处于平衡超高状态时,仅有从动轮对外轮-外轨的横向黏滑曲线出现了负斜率现象,即从动轮对的外轮-外轨有发生横向黏滑扭振的可能性,但是其出现负斜率时所需的黏着系数(0.062)较大,因此振动强度较弱且发生概率较低.其他轮轨黏滑特性曲线未出现明显负斜率现象,表明相应的轮轨界面不会发生黏滑扭振,即不会形成钢轨波磨.
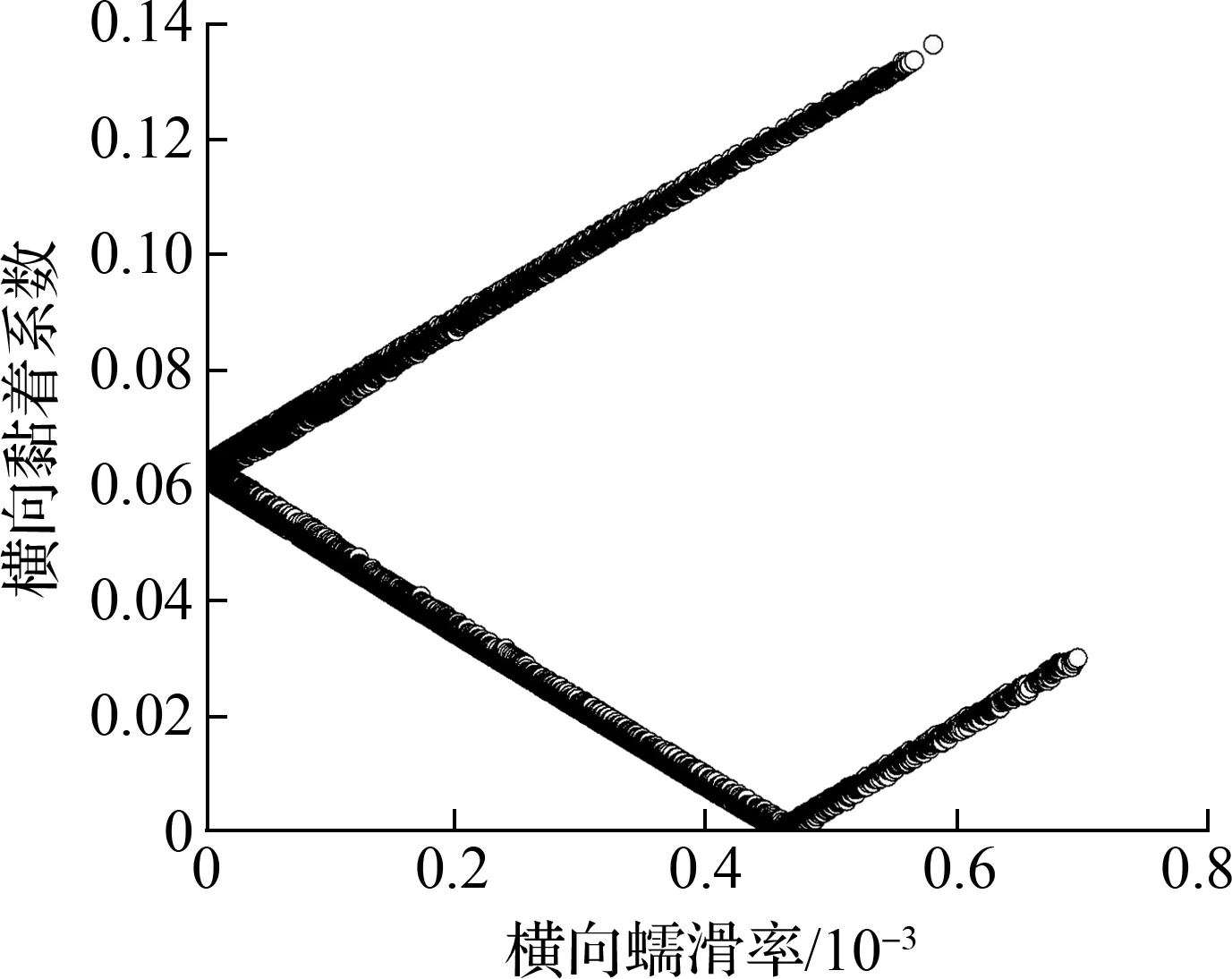
由图17和图18可知,当轨道处于过超高状态时,从动轮对外轮-外轨的横向黏滑曲线也出现了负斜率现象,且所需黏着系数(0.061)仍然较大.然而,不同于轨道欠超高和平衡超高工况的是,轨道过超高会导致导向轮对外轮-外轨的横向黏滑特性曲线出现负斜率现象,但是由于所需黏着系数(0.190)较大,所以振动强度较弱.其他轮轨黏滑曲线未见明显负斜率区间,说明相应的轮轨界面不会形成黏滑扭振,即不会产生钢轨波磨.
(a) 内轮-内轨纵向黏滑曲线

(b) 内轮-内轨横向黏滑曲线
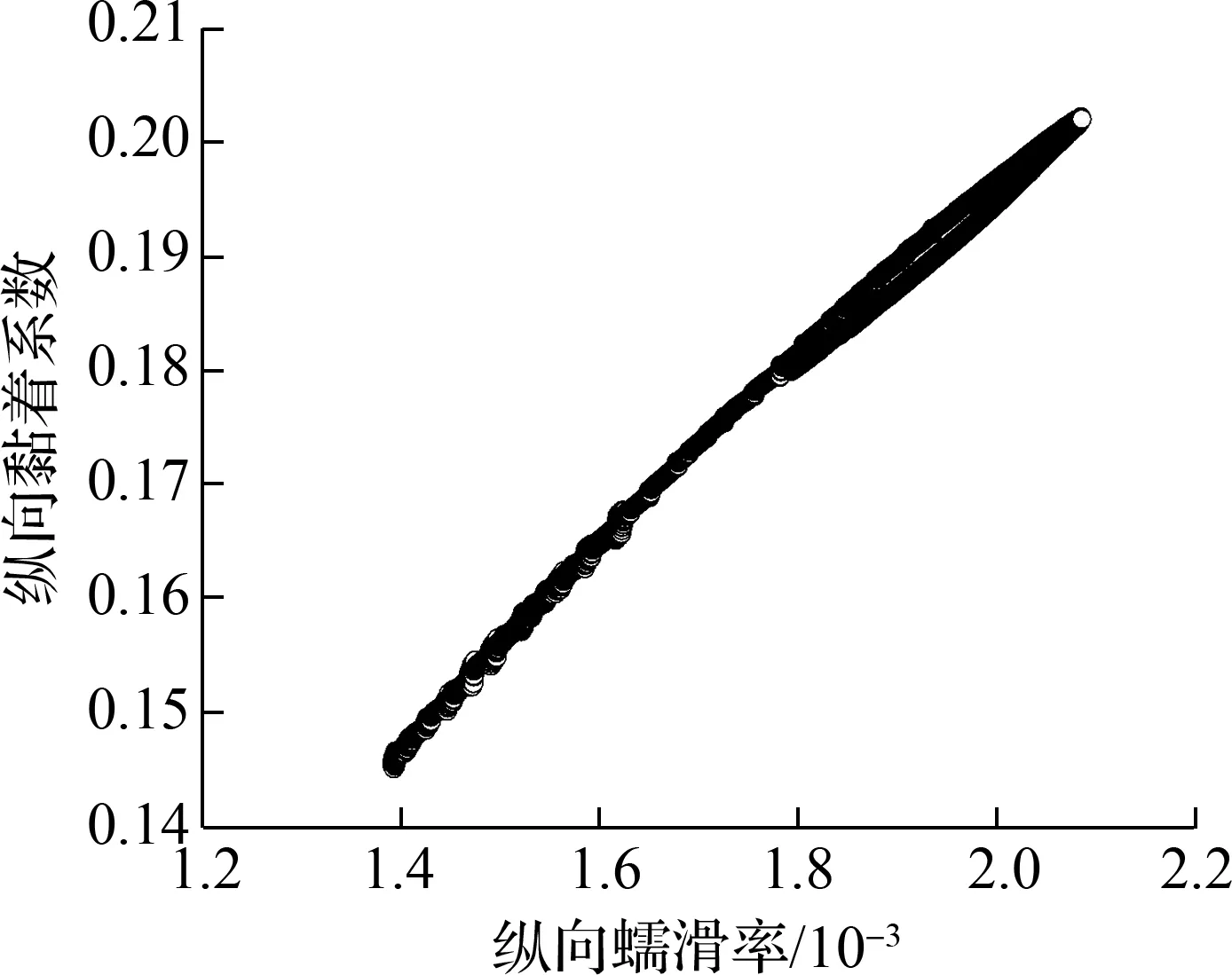
(c) 外轮-外轨纵向黏滑曲线

(d) 外轮-外轨横向黏滑曲线

(a) 内轮-内轨纵向黏滑曲线
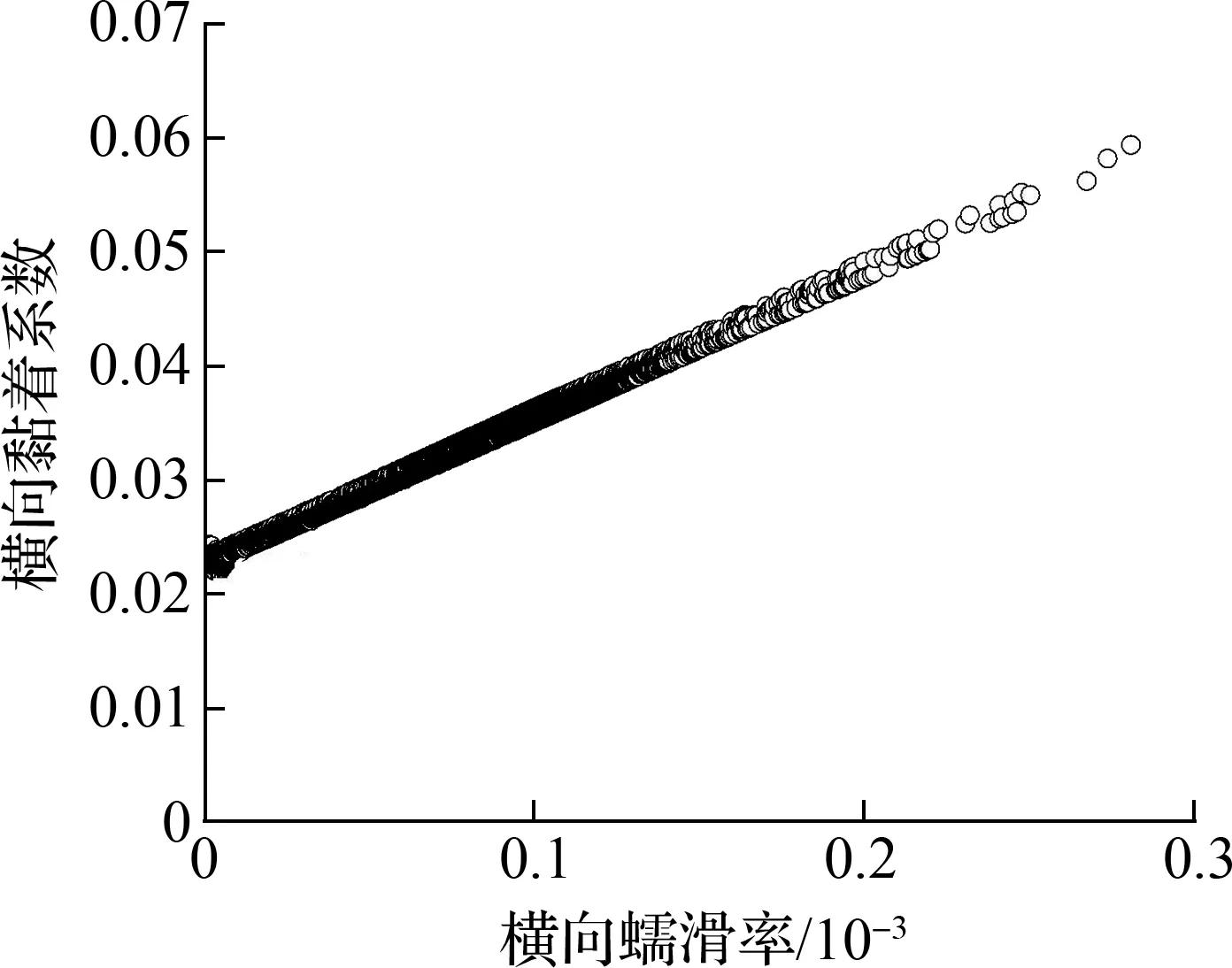
(b) 内轮-内轨横向黏滑曲线

(c) 外轮-外轨纵向黏滑曲线
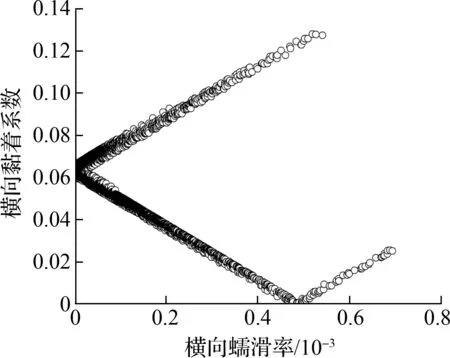
(d) 外轮-外轨横向黏滑曲线
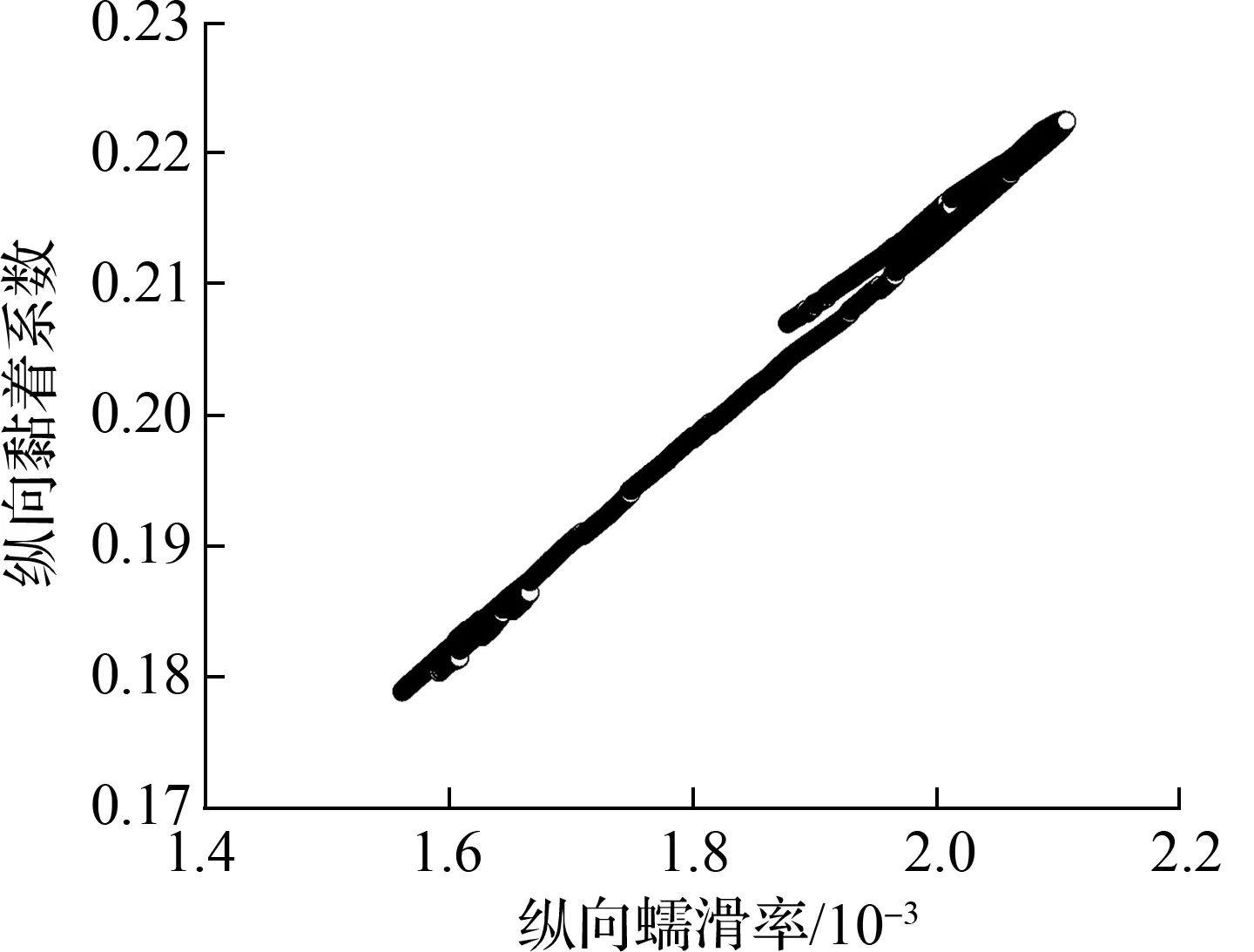
(a) 内轮-内轨纵向黏滑曲线
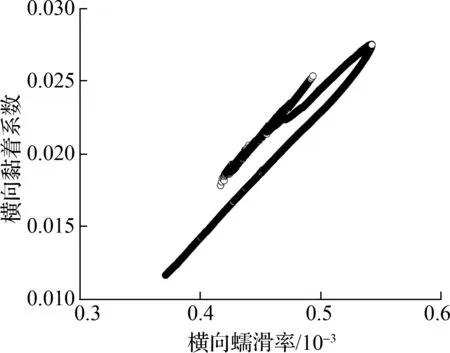
(b) 内轮-内轨横向黏滑曲线
(c) 外轮-外轨纵向黏滑曲线
(d) 外轮-外轨横向黏滑曲线
结合2.3节轨道欠超高工况可以得出,随着轨道超高的增加(欠超高-平衡超高-过超高),内轨波磨的发生趋势逐渐降低,尤其当轨道超高达到平衡以后,内轮-内轨界面将不存在黏滑负斜率现象,说明内轨此时将不容易形成波磨;外轨则始终存在发生波磨的可能性,只是发生概率相对较低.上述分析表明,超高状态影响着曲线轨道轮轨黏滑负斜率的形成机制,即轨道超高状态是引发横向滑移(内轮-内轨界面)产生的原因之一,从而决定了钢轨波磨的发生概率.因此,实际地铁线路施工过程中,适当地提高轨道超高值可以有效地减缓小半径曲线上的内轨波磨现象.
(a) 内轮-内轨纵向黏滑曲线

(b) 内轮-内轨横向黏滑曲线
(c) 外轮-外轨纵向黏滑曲线
(d) 外轮-外轨横向黏滑曲线
本文是在一个配置为Inter (R) Xeon (R) W-2245 CPU (3.90 GHz)和64.0 GB RAM的计算机环境下,采用2.1节中的轮轨接触算法计算2.3节及第4节所述的3种工况,每种工况的计算时间平均约为35 min.
5 结论
1)现场调研及数据分析发现,内轨轨面波磨较为严重,且波磨主要特征波长为40 mm;外轨存在侧面波磨,整体程度相对轻微.
2)轮轨黏滑扭振特性分析显示,导向轮对内轮-内轨的横向黏滑扭振促使了内轨波磨的形成,从动轮对外轮-外轨也有发生横向黏滑扭振的可能性,但是强度较弱且概率较低,因此在小半径曲线上内轨波磨较为严重,外轨波磨则整体相对轻微或部分区间不存在,这与线路实测情况相符.
3)超高状态影响着曲线轨道轮轨黏滑负斜率的形成机制,从而决定了钢轨波磨的发生概率,因此实际地铁线路施工中,适当地提高轨道超高可以有效地减轻小半径曲线上的内轨波磨程度.
