基于BP-改进NSGA-Ⅱ锅炉燃烧多目标优化

徐文韬 黄亚继 曹歌瀚 陈 波 金保昇

(1东南大学能源热转换及其过程测控教育部重点实验室， 南京 210096)(2江苏方天电力技术有限公司， 南京 211102)

2020年10月，国家能源局发布的1—9月份全国电力工业统计数据[1]显示，全国全社会用火电量累积达121 579万kW·h，远高于水电、核电和风电用电量.我国燃煤发电在煤炭消费领域中仍然占据重要位置，要实现2030年碳达峰和2060年碳中和目标，除了加快清洁能源开发利用和推动能源转型，将旧煤电改造为高质量燃煤发电迫在眉睫.

国外研究者Kalogirou[2]、Booth等[3]和Qin等[4]将人工智能技术应用于电站锅炉燃烧优化控制技术的研究.王培红等[5]基于神经网络建立了NOx排放模型与锅炉热效率模型，同时结合遗传算法并通过权值组合对锅炉NOx排放和锅炉热效率实现燃烧优化.肖勇等[6]将人工群峰(ABC)优化方法应用于锅炉燃烧，以提高锅炉燃烧效率和降低NOx排放.索新良等[7]进行一次风调平、煤粉细度调整、燃尽风运行及配风调整、二次风配风调整等调整试验，解决四角切圆锅炉热效率偏低和炉膛出口烟温偏差较大的问题.薛晓波等[8]基于模型辨识的预测控制技术，开展在线测量研究和闭环调整控制，实现锅炉燃烧实时调整.董胡适等[9]提出一种基于量子遗传算法(QGA)和神经网络(ANN)的混合优化方法以提高锅炉热效率和降低NOx排放量，实现锅炉燃烧对热效率和氮氧排放量的整体优化.张国斌等[10]设计了一种基于数据挖掘案例推理的电站锅炉燃烧优化系统，以提高锅炉热效率和降低氮氧化合物排放.Niu等[11]基于案例推理原理提出一种新型的燃煤锅炉在线燃烧优化方法，优化结果使锅炉热效率提高 0.68%，NOx排放不超标.顾燕萍等[12]、高芳等[13]和刘吉臻等[14]采用最小二乘支持向量机建立电站锅炉燃烧模型，有效地预测锅炉热效率并实现飞灰含碳量、NOx排放量的软测量.Li等[15]研究一种基于偏维对立学习粒子群优化的低NOx燃烧优化技术，并证明该技术使NOx排放质量浓度降低37.72 mg/m3.Niu等[16]提出一种改进的极限学习机，基于该方法建立了330 MW循环流化床锅炉的热效率模型和NOx排放模型，并验证该方法用于构建锅炉燃烧模型的可靠性.Tang等[17]提出一种自适应数据驱动的建模方法用以动态预测锅炉NOx排放，并验证该建模方法的正确性.谷丽景等[18]基于热态正交试验和人工神经网络建立锅炉燃烧优化混合模型，实现NOx排放、飞灰含碳量及炉膛温度等参数软测量.Zhou等[19]结合人工神经网络和遗传算法(ANN-GA)建立锅炉燃烧优化模型，并确定最佳燃烧优化解决方案，以降低碳含量排放和NOx排放.Song等[20]结合改进的广义回归神经网络(IGRNN)和改进人工蜂群 (IABC)提出了一种全新的锅炉燃烧优化方法，并以燃烧成本计算方式为目标函数，验证该方法的有效性.Ma等[21]提出了一种基于修正教学的多目标优化方法，以提高热效率和降低NOx/SO2排放质量浓度，实现循环流化床锅炉燃烧的优化.

然而，在上述锅炉燃烧优化工作中，学者们通过权值组合方法将多目标优化转换为单目标优化，锅炉燃烧系统具有多变量强耦合特性且锅炉内各个变量量纲不统一，无法通过对单一目标优化使锅炉内燃烧系统整体获得优化，采取权值组合方法将多目标优化转换为单目标优化时，各目标权重选择又存在人为因素导致无法客观优化，因此全面客观地对锅炉燃烧系统进行多目标优化是目前的研究方向.

NSGA-Ⅱ优化算法核心内容为通过协调各目标函数间关系，在约束条件范围内搜索到目标函数均沿期望方向变化的最优解或者Pater最优解.改进NSGA-Ⅱ优化算法[22-23]在交叉运算时，以NDX算子代替SBX算子扩大搜索空间，有效地避免陷入局部最优和进化不稳定情况.因此，本文结合BP神经网络与改进非支配排序遗传算法(INSGA-Ⅱ)，提出一种基于BP-INSGA-Ⅱ的锅炉燃烧优化模型.首先基于BP神经网络建立锅炉燃烧系统NOx排放质量浓度预测模型和锅炉热效率预测模型；其次，基于INSGA-Ⅱ优化算法对锅炉燃烧系统进行多目标寻优；最后，基于BP-INSGA-Ⅱ算法、BP-NSGA-Ⅱ算法、GRNN-INSGA-Ⅱ算法和GRNN-NSGA-Ⅱ算法分别建立锅炉燃烧优化模型，比较这4种燃烧优化模型的优化结果和训练时间，验证该优化模型的有效性.

1 目标函数模型建立

锅炉内燃烧系统具有多变量、强耦合且复杂多变特性，难以直接采用明确的数学表达建立锅炉燃烧系统模型.借助人工神经网络善于处理“黑箱”问题且具有强非线性映射能力和良好的泛化能力，本文基于BP神经网络建立锅炉燃烧系统预测模型.

以锅炉热效率和NOx排放质量浓度为目标参量，由锅炉热平衡计算理论可知，飞灰含碳量和排烟温度直接影响锅炉热效率，而飞灰含碳量和排烟温度主要受燃烧器二次风配风方式、分离燃尽风设置方式、烟气含氧量等因素影响.分析NOx生成机理可知，NOx的生成机制主要分为热力型NOx和燃料型NOx，其排放主要与炉膛温度水平和分离燃尽风配比有关，即

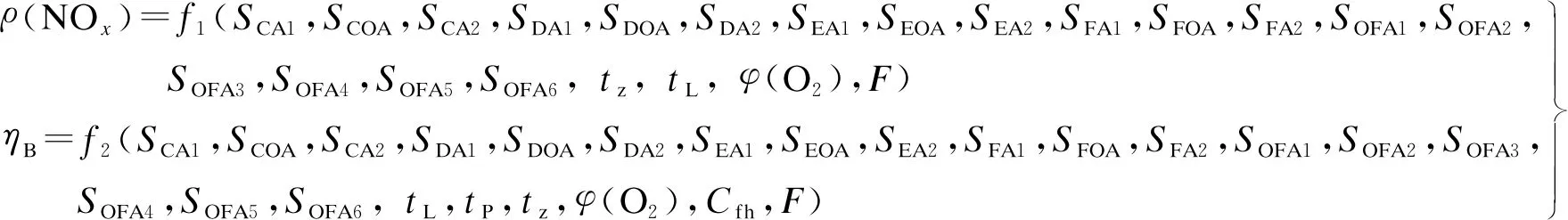
(1)

式中，ρ(NOx)为NOx排放质量浓度；SCA1～SFA2为12层二次风风门开度；SOFA1～SOFA6为6层分离燃尽风风门开度；tz为主蒸汽温度；tL为空气预热器进口烟气温度；φ(O2)为省煤器烟气含氧量(体积分数)；F为锅炉负荷；ηB为锅炉热效率；tP为排烟温度；Cfh为飞灰含碳量(体积分数)；f1为NOx排放质量浓度计算函数；f2为锅炉热效率计算函数.

以新海燃煤电厂的超临界燃煤机组为研究对象，从电厂分散控制系统(DCS)采集600、700和800 MW这3种负荷工况数据，包含12层二次风风门开度(SCA1、SCOA、SCA2、SDA1、SDOA、SDA2、SEA1、SEOA、SEA2、SFA1、SFOA、SFA2)、6层燃尽风风门开度(SOFA1、SOFA2、SOFA3、SOFA4、SOFA5、SOFA6)、主蒸汽温度、空气预热器进口烟气温度、排烟温度、省煤器出口烟气含氧量、飞灰含碳量等参量.表1列出电厂采集试验数据.其中，排烟温度取自空气预热器出口温度，飞灰含碳量由电厂取样检测获得，锅炉热效率按锅炉热平衡计算求得.另外，燃烧器布置简图如图1所示.

表1 电厂试验数据

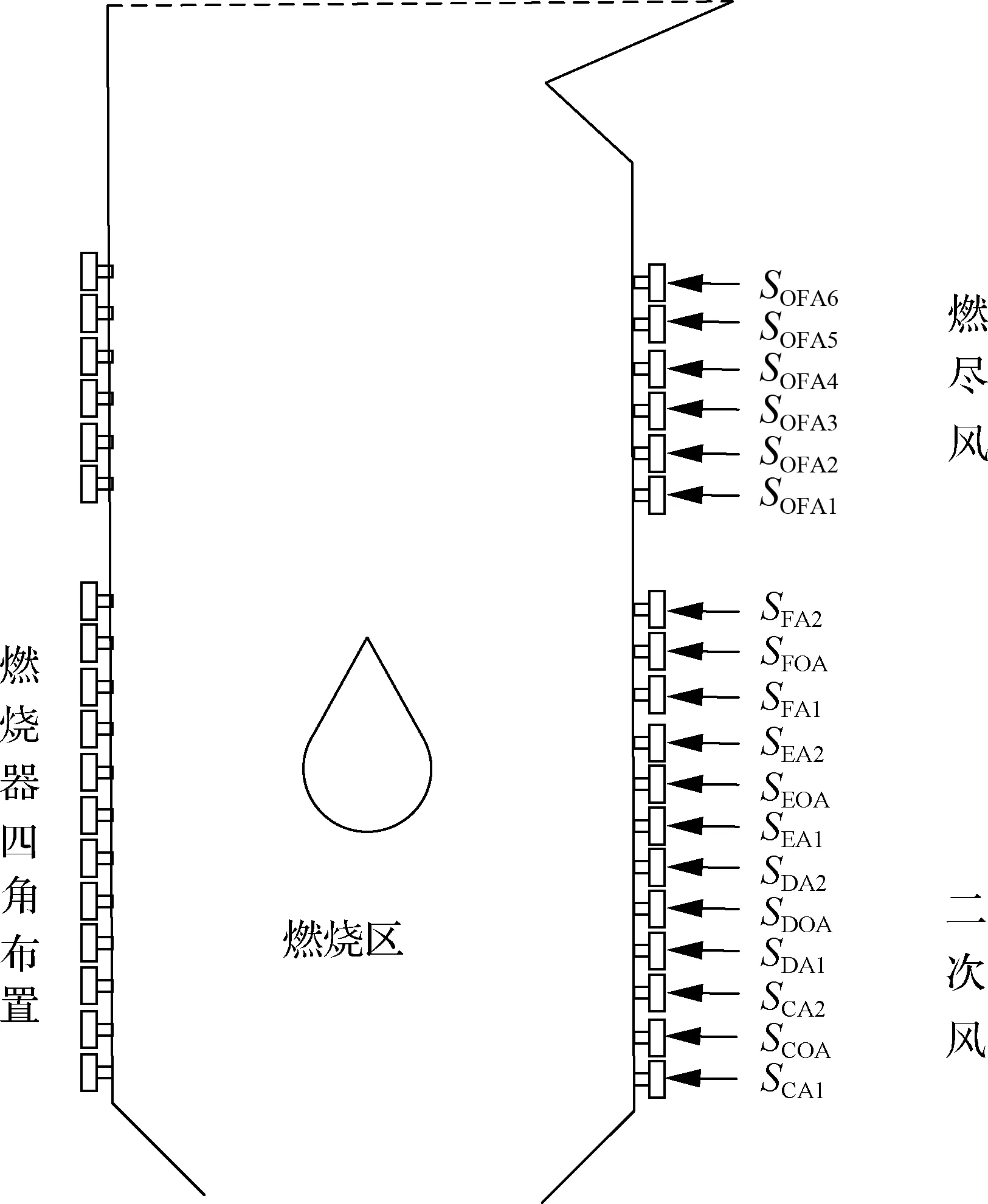
图1 燃烧器布置示意图

2 BP建模及模型预测

根据锅炉燃烧特性、NOx生成机理和锅炉热效率影响因素，基于BP神经网络建立NOx排放质量浓度预测模型和锅炉热效率预测模型.NOx排放质量浓度预测模型的输入层变量为二次风风门开度、燃尽风风门开度、空气预热器进口烟气温度、主蒸汽温度、省煤器出口烟气含氧量和锅炉负荷等变量.锅炉热效率预测模型的输入层变量为二次风风门开度、燃尽风风门开度、空气预热器进口烟气温度、主蒸汽温度、排烟温度、省煤器烟气含氧量、飞灰含碳量和锅炉负荷等变量.

首先，基于ANN1神经网络建立锅炉飞灰含碳量和排烟温度预测模型；其次，基于ANN2神经网络建立锅炉热效率预测模型；最后，基于ANN3神经网络建立NOx排放质量浓度预测模型.其中，ANN1神经网络隐含层层数为1，其节点数设为8，隐含层激励函数为tansig函数；ANN2和ANN3神经网络隐含层层数为2，节点数分别为8和4，隐含层激励函数分别选取tansig函数和purelin函数.

选取前95%试验数据样本作为神经网络训练样本，剩余样本作为检验样本，以验证神经网络模型有效性.其预测结果如图2所示.

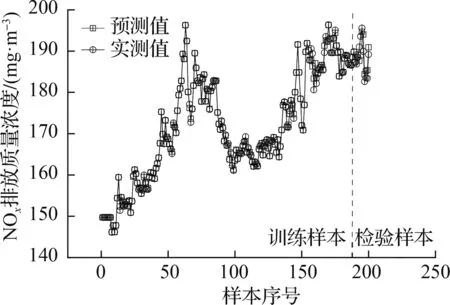
(a) NOx排放质量浓度预测模型

(b) 锅炉热效率预测模型

由图2可知，检验样本中，NOx排放质量浓度预测模型和锅炉效率预测模型的预测值与其对应的实际值之间的偏差均较小.2种模型预测值与实际值相对误差分别如表2和表3所示.由表可知，2种预测模型最大误差均不超过3%.结果表明：基于BP神经网络建立NOx排放质量浓度预测模型和锅炉热效率预测模型结果较精确.

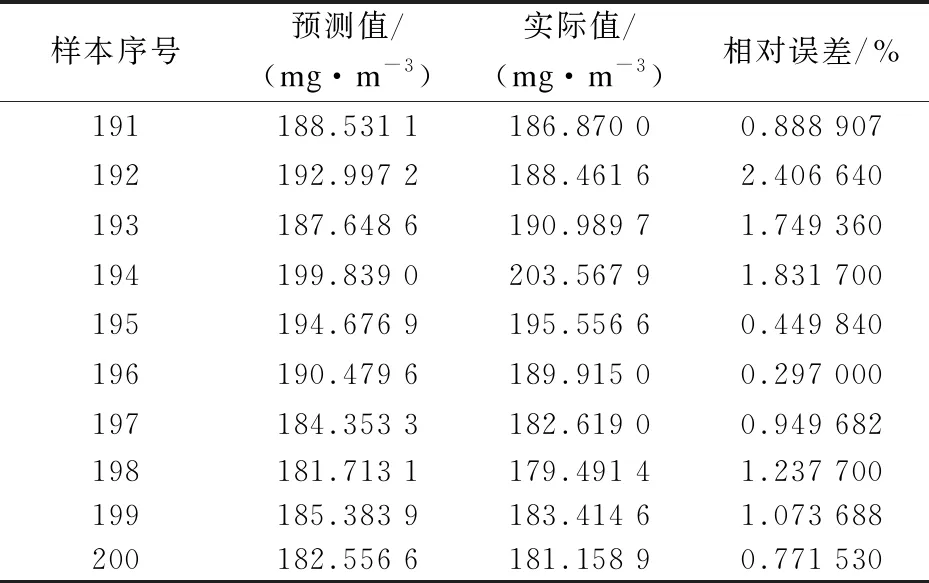
表2 NOx排放质量浓度模型预测值与实际值比较

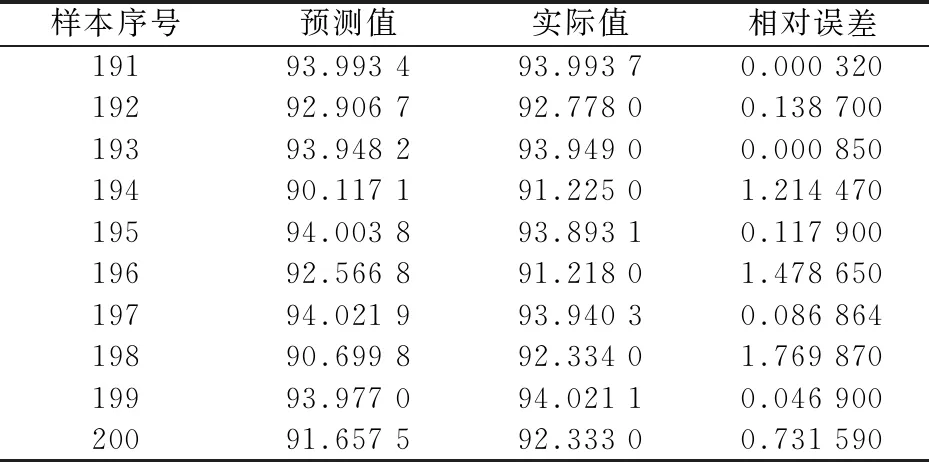
表3 锅炉热效率模型预测值与实际值比较 %

3 改进NSGA-Ⅱ多目标燃烧优化

NSGA-Ⅱ算法原理是通过协调各个目标函数之间关系，使目标函数在约束条件范围内搜索到一组最优解或Pater最优解.与传统NSGA算法相比，该算法引入快速排序法构造非支配解集和精英保留策略，避免对共享参数的确定及动态调整和修改，并用拥挤度代替共享参数来保持解群体的分布性和多样性，有利于提高优化算法效率和降低算法计算时间复杂度.与传统NSGA-Ⅱ算法相比，改进NSGA-Ⅱ算法将NDX算子引入到NSGA-Ⅱ算法中，解决了SBX算子搜索空间范围窄的问题，有利于增强群体多样性和避免优化算法出现早熟现象或陷入局部最优.NDX算子为

(2)

式中，C1/2i为子代染色体上对应的第i个变量；y1i、y2i为2个父代染色体对应的第i个变量；N(0,1)为正态分布随机变量；u为在(0,1)区间上均匀分布的随机数.

采用ZDT1测试函数验证NDX算子空间搜索能力.设置自变量个数为10，目标函数个数为2，经种群初始化、快速非支配排序、拥挤度计算和选择等操作获得父代种群.基于SBX算子和NDX算子产生子代个体，循环计算100次，分别产生200个子代，获得2种算子在搜索空间的分布情况如图3所示.ZDT1测试函数如下：

(3)

s.t.

g1(x,y)=(x-5)2+y2≤25
g2(x,y)=(x-8)2+(y+3)2≥7.7
0≤x≤5, 0≤y≤3

(4)

(a) SBX算子

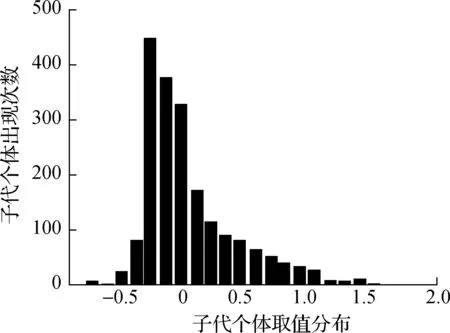
(b) NDX算子

由图3可知，基于NDX算子多目标优化算法提高优化算法空间搜索能力，增强群体多样性.

锅炉燃烧系统中，提高锅炉热效率与降低NOx排放质量浓度两者相互矛盾.NSGA-Ⅱ算法基于快速排序法对每个子目标函数进行排序，不需采用权值组合法将多目标优化转换为单目标变化，各子目标均可沿期望方向进行优化.为此，提出3种锅炉燃烧优化方案：① 将提高锅炉热效率和降低NOx排放质量浓度同时作为锅炉燃烧优化的主要优化方向；② 在NOx排放质量浓度符合国家安全排放标准下，以提高锅炉热效率为主要优化方向，此时f1目标函数值排序方向随f2目标函数值排序方向进化；③ 规定锅炉热效率在某一范围，即不以提高锅炉热效率为必要优化目标时，以降低锅炉NOx排放质量浓度为主要优化方向，此时f2目标函数值排序方向随f1排序方向进化.有

(5)

(6)

(7)

式中，f1↓表示NOx排放质量浓度快速排序方向依据降低NOx排放质量浓度方向进行；f1↑表示NOx排放质量浓度快速排序方向依据提高锅炉热效率方向进行；f2↓表示锅炉热效率快速排序方向依据降低NOx排放质量浓度方向进行；f2↑表示锅炉热效率快速排序方向依据提高锅炉热效率方向进行.其中，根据锅炉历史燃烧数据及理论经验获得自变量范围，SCA1∈[0,100%]，SCOA∈[0,100%]，SCA2∈[0,100%]，SDA1∈[0,100%]，SDOA∈[0,100%]，SDA2∈[0,100%]，SEA1∈[0,100%]，SEOA∈[0,100%]，SEA2∈[0,100%]，SFA1∈[0,100%]，SFOA∈[0,100%]，SFA2∈[0,100%]，SOFA1∈[0,100%]，SOFA2∈[0,100%]，SOFA3∈[0,100%]，SOFA4∈[0,100%]，SOFA5∈[0,100%]，SOFA6∈[0,100%]，tz∈[582.90 ℃，607.46 ℃]，tL∈[342.6 ℃，294.0 ℃]，tP∈[87.90 ℃, 117.54 ℃]，φ(O2)∈[1.66%,6.8%]，Cfh∈[2.167%, 2.169%]，F∈[375.39 MW, 912.49 MW].

结合BP神经网络强非线性映射能力和NSGA-Ⅱ多目标优化算法快速非支配排序能力，建立一套基于BP-INSGA-Ⅱ的锅炉燃烧优化模型：

① 锅炉负荷、辅助风风门开度、燃尽风风门开度、烟气含氧量、排烟温度、飞灰含碳量、空气预热器进口烟气温度、主蒸汽温度等参数采用实数编码.

② 设定种群个体大小N，确定种群中各个决策变量上限与下限，生成初始种群，每一个个体均代表一种规划方案.

③ 计算初始种群目标函数值.基于BP神经网络建立的NOx排放预测模型和锅炉热效率预测模型计算初始种群每个粒子对应的NOx排放和锅炉热效率.

④ 基于快速非支配排序方法将进化群体的子目标函数值快速分层，获得进化群体每个个体非支配层序号.非支配层序号越靠前，优良个体越靠近Pater前沿，进化群每个个体拥挤度都可以通过计算与其相邻2个个体在每个子目标上的距离差之和来求取，保持解群体分布性和多样性.

⑤ 在进化过程中，选择操作的目的是为了防止有效基因丢失，剔除无效个体，使优化过程朝着Pater最优解的方向进化.根据进化群中每个个体非支配等级和拥挤度这2个量，采用锦标赛选择算子对种群中所有个体进行选择.选择原则为排序等级优先权高于拥挤度的优先权，排序等级高的个体优于排序等级低的个体，拥挤度大的个体优于拥挤度小的个体.

⑥ NDX算子交叉和多项式变异操作使搜索空间更加广阔，避免优化过程陷入局部最优的问题，实现全局优化.

⑦ 将父代优良个体以概率为1的方式遗传给子代，完全保留父代种群的优良.将父代个体与子代个体重新合成新种群，依据新种群目标函数进行快速非支配排序和拥挤度操作获得新的父代种群.

⑧ 循环①～⑥操作，直到满足收敛条件算法停止.同时获得Pater最优解集，采用模糊隶属度计算每个Pater最优解满意度，比较获得Pater最优解满意度最大的个体，即最优折中解.

4 基于BP-INSGA-Ⅱ仿真优化

以表1电厂数据为优化群体构造初始种群，种群规模为200，设置迭代次数200，交叉概率为0.9，变异概率为0.1，优化目标为NOx排放质量浓度和锅炉热效率，基于BP-INSGA-Ⅱ优化方法对方案1、方案2和方案3进行仿真寻优，结果见图4～图7.

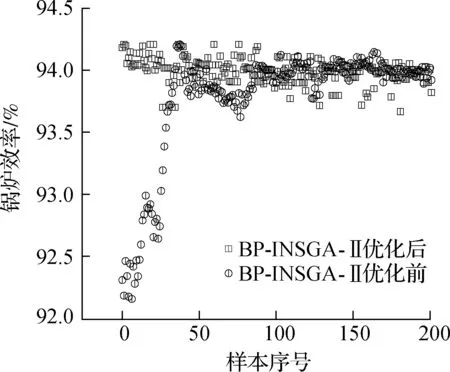
采用BP-INSGA-Ⅱ优化算法进行种群寻优，依据目标优化方向进行非快速排序和拥挤度计算，并要求同时比较任意2个样本的NOx排放质量浓度和锅炉热效率以确定该两样本间Pater解支配关系，NOx排放质量浓度期望降低其浓度值，锅炉热效率期望升高其效率值.针对方案1，基于BP-INSGA-Ⅱ燃烧优化模型优化NOx排放质量浓度和锅炉热效率，其结果如图4和图7所示.由图4(a)可知，种群内93%样本NOx排放质量浓度低于优化前NOx排放质量浓度，远远低于国家安全标准要求排放值[24]，剩下7%样本NOx排放质量浓度高于优化前NOx排放质量浓度，而对应的锅炉热效率高于优化前锅炉热效率，如图7(a)所示.在方案1锅炉热效率优化进程中，锅炉热效率会产生一些低于未优化时锅炉热效率的折中解，如图4(b)所示，以黑色线标注该折中解区域，而折中解对应的NOx排放质量浓度远远低于优化前NOx排放质量浓度.由图4(b)可知，种群内40%样本锅炉热效率低于优化前锅炉热效率，而对应NOx排放质量浓度低于未优化时样本NOx排放质量浓度，正如图7(b)所示；另外，种群内部分样本NOx排放质量浓度和锅炉热效率均趋向各期望方向进化，正如图7(c)所示.

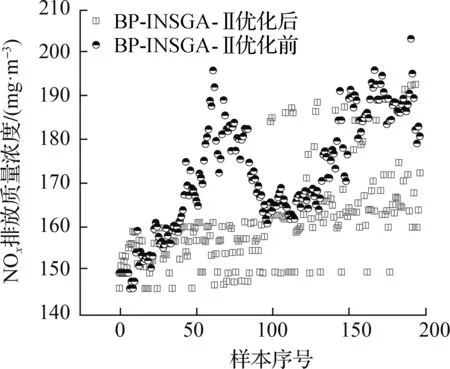
(a) NOx排放质量浓度

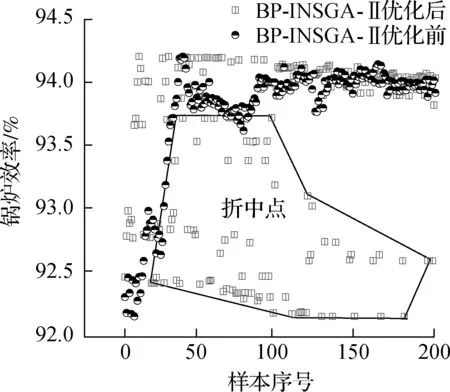
(b) 锅炉热效率

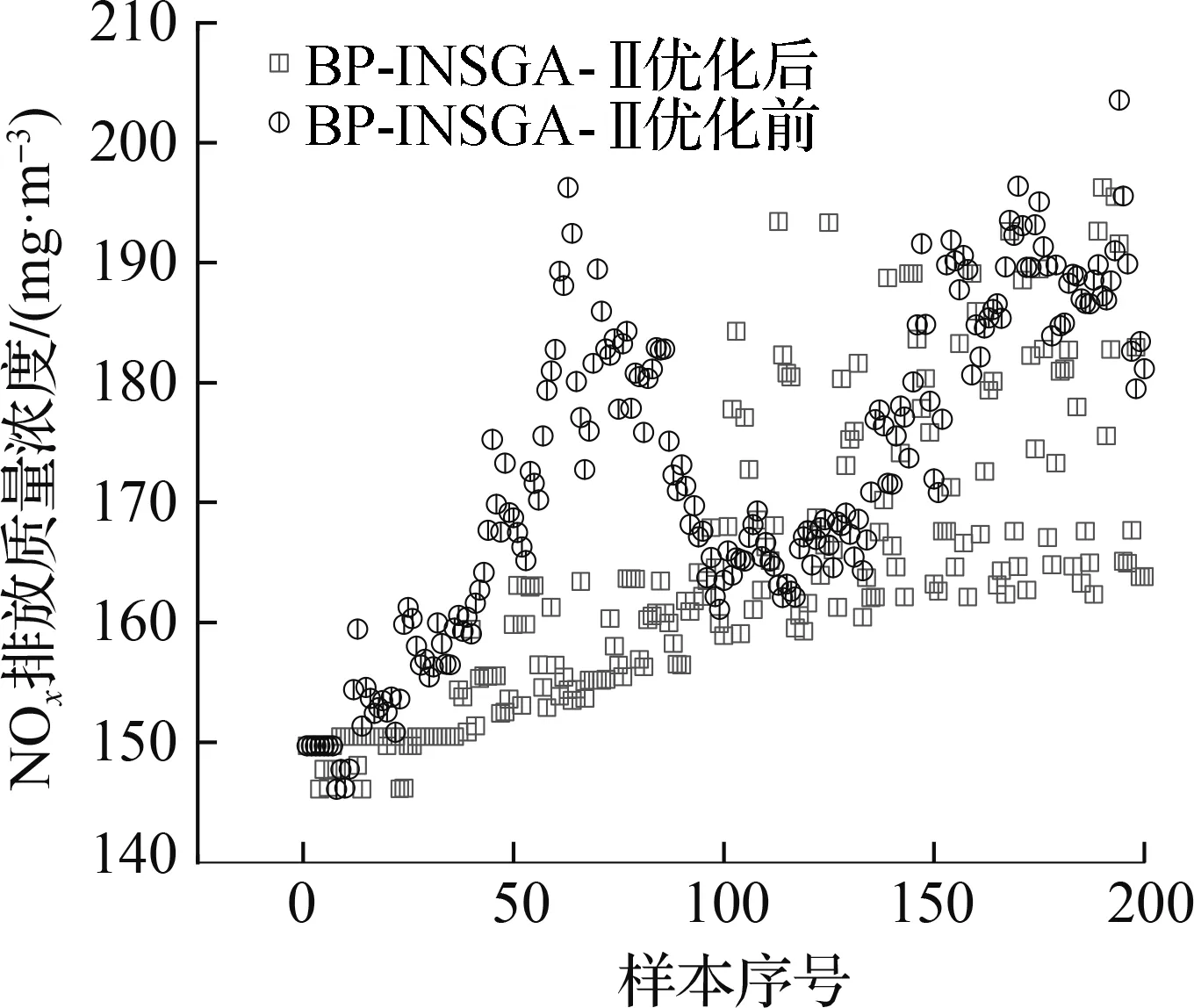
(a) NOx排放质量浓度

(b) 锅炉热效率

(a) NOx排放质量浓度

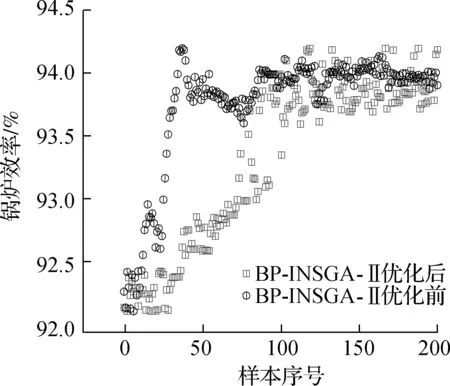
(b) 锅炉热效率

方案2以提高锅炉热效率为主要优化方向，基于BP-INSGA-Ⅱ燃烧优化模型优化NOx排放质量浓度和锅炉热效率，结果如图5所示.基于BP-INSGA-Ⅱ优化模型优化后，锅炉热效率和NOx排放质量浓度均大于未优化时NOx排放质量浓度和锅炉热效率.前30个样本锅炉热效率由92%升高至94.3%，NOx排放质量浓度由150 mg/m3升高至近200 mg/m3，种群中95%样本的锅炉热效率高于优化前锅炉热效率.NOx排放质量浓度小于250 mg/m3，符合国家安全生产范围时，可采取方案2指导电厂锅炉燃烧优化.

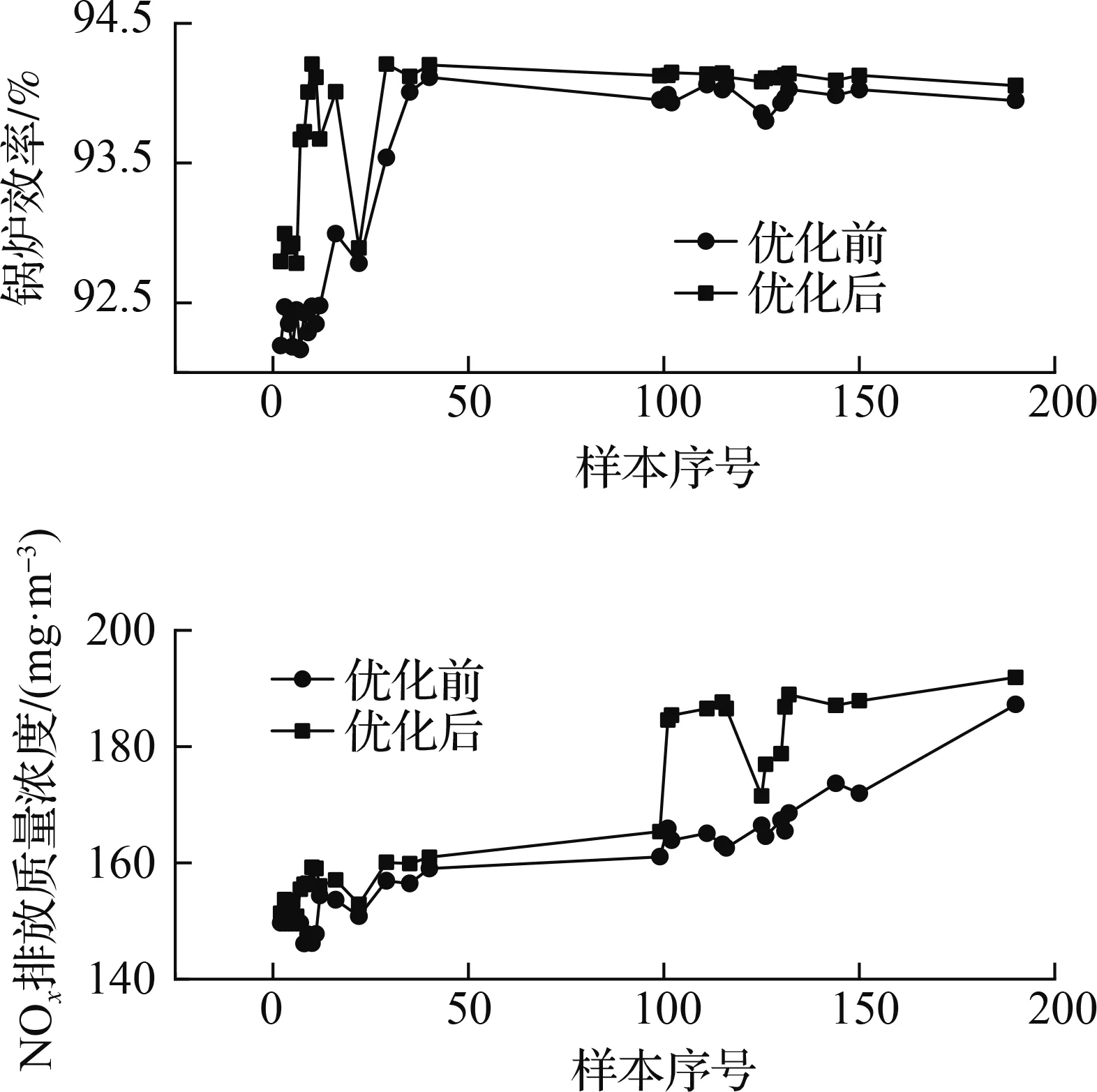
(a) 7%样本优化

(b) 40%样本优化

(c) 部分样本优化

方案3以降低锅炉NOx排放质量浓度为主要优化方向.基于BP-INSGA-Ⅱ优化模型优化NOx排放质量浓度和锅炉热效率，其结果如图6所示.优化后锅炉热效率和NOx排放质量浓度均小于未优化时的NOx排放质量浓度和锅炉热效率，95%样本的NOx排放质量浓度低于优化前NOx排放质量浓度，当锅炉热效率满足电力企业经济生产要求时，可采取方案3指导电厂锅炉燃烧优化.

5 验证优化模型

基于BP-INSGA-Ⅱ算法、BP-NSGA-Ⅱ算法、GRNN-INSGA-Ⅱ算法和GRNN-NSGA-Ⅱ算法分别建立锅炉燃烧优化模型，并比较这4种多目标燃烧优化模型的优化结果和训练时间，以验证BP-INSGA-Ⅱ锅炉燃烧优化模型的有效性，结果如表4所示.

表4 不同燃烧优化模型的性能比较

由表4可知，4种多目标锅炉燃烧优化模型均能降低NOx排放质量浓度，而平均锅炉热效率在10-3量级范围内有升高或降低趋势；相比另外3种锅炉燃烧优化模型，基于BP-INSGA-Ⅱ算法建立的锅炉燃烧优化模型在短时间内获得低NOx排放质量浓度和相对较高的锅炉热效率；基于BP-INSGA-Ⅱ算法建立的锅炉燃烧优化模型使锅炉热效率平均升高0.105 8%，NOx排放质量浓度平均降低15.42%，远优于其他优化模型优化结果.结果表明：基于BP-INSGA-Ⅱ算法建立的锅炉燃烧优化模型能获得相对较高的锅炉热效率和低NOx排放质量浓度，进而促进燃煤电厂在新能源发电市场中的竞争地位.

表5表示基于BP-INSGA-Ⅱ算法建立的锅炉燃烧优化模型获得最优目标推荐值，将最优目标推荐值反馈给电厂运行人员，可指导锅炉燃烧过程.

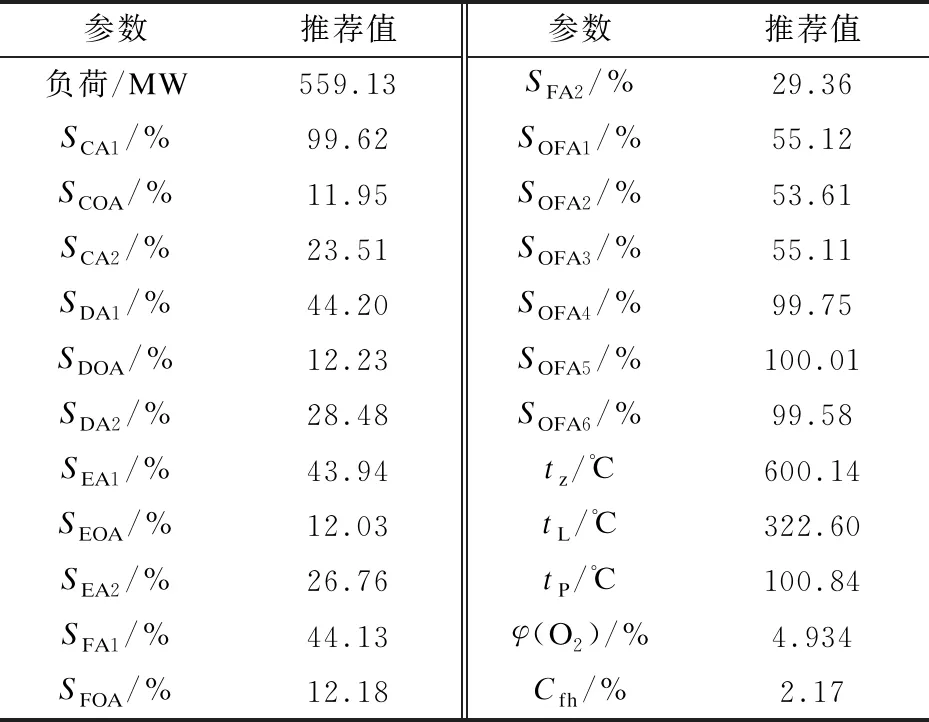
表5 最优目标函数对应自变量推荐值

6 结论

1) 基于BP神经网络建立锅炉燃烧系统NOx排放质量浓度预测模型与锅炉热效率预测模型，其相对误差均小于3%，证明了本文所构建2个预测模型的精确性.

2) 采用方案1，NOx排放质量浓度和锅炉热效率均沿期望方向进化时，种群内93%样本NOx排放质量浓度低于优化前NOx排放质量浓度，大部分样本锅炉热效率高于优化前锅炉热效率.

3) 采用方案2，NOx排放质量浓度进化方向随锅炉热效率期望方向进化时，种群内95%样本的锅炉热效率高于优化前锅炉热效率.

4) 采用方案3，锅炉热效率进化方向随NOx排放质量浓度期望方向进化时，种群中95%样本的NOx排放质量浓度低于优化前NOx排放质量浓度.

5) 基于BP-INSGA-Ⅱ算法建立的锅炉燃烧优化模型能在短时间内获得低NOx排放质量浓度和相对较高的锅炉热效率，NOx排放质量浓度平均降低15.42%，锅炉热效率平均升高0.105 8%，验证了该优化模型的有效性.