沙漠绿洲地区地下水数值模型的参数灵敏度分析

李 飞，李松达，单圣苏，唐石振，王霞雨，刘佩贵

(合肥工业大学土木与水利工程学院，安徽 合肥 230009)

0 引言

地下水在维持沙漠绿洲区生态环境健康方面发挥着至关重要的作用，但受地理位置和参数空间变异性等因素的制约，地下水数值模型建立过程中存在众多不确定性因素，严重影响到地下水资源评价结果及数值模型结果的可靠度。因此，需要开展数值模型的参数灵敏度分析，目前局部灵敏度分析方法较成熟，也广泛应用于地下水数值模型中[1]。全局灵敏度分析方法的研究成果主要有多元回归法[2]、Morris法[3]、扩展傅里叶幅度灵敏度检验法(EFAST)[4]以及Sobo’l法[5]等。为进一步对比分析局部与全局灵敏度分析结果的异同，本文以塔克拉玛干沙漠南缘的绿洲为例，在参数局部灵敏度分析的基础上结合全局灵敏度分析方法(Morris法)，以地下水水位变幅作为分析对象，对该绿洲地区的地下水数值模型进行局部和全局灵敏度分析，以期为指导沙漠绿洲区地下水资源的开发利用提供技术支撑。

1 研究区地下水数值模型

1.1 研究区概况

研究区位于塔克拉玛干大沙漠的西南缘的皮山县，区内主要河流为皮山河。流域内赋存有第四系松散堆积层孔隙潜水；第三系碎屑岩裂隙孔隙水及层间承压水；以泥盆系、志留系、二迭系、侏罗系和白垩系为主的碎屑岩裂隙潜水；地下水的赋存、分布具有明显的分带性，水文地质结构如图1所示。

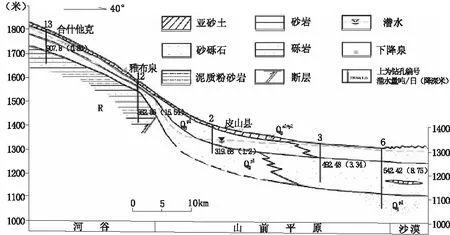
图1 山前水文地质剖面示意图

皮山河发源于喀喇昆仑山北麓，上游由阿克肖河及康艾孜河两大支流组成，两支流在瑙阿巴提塔吉克民族乡汇合，由南向北流经克里阳注入雅普泉水库，后流经皮山县城消失于塔克拉玛干大沙漠，全长160 km，皮山河流域形似一羽毛状。皮山河水文站以上集水面积为1 894.7 km2，径流系数为17.52×104m3/km2，海拔高程在2 300～5 500 m之间，河流长度为72 km，河源最高点海拔6 000 m以上。在5 500 m以上的高山区分布有大量的冰川和积雪。多年平均降水量仅171.2 mm左右，雪线以上冰川和永久积雪区年降水量可达500 mm左右，出山口后平原区多年平均降水量仅为48.2 mm左右，高山区冰雪消融水和中浅山区降雨是皮山河径流的主要补给源。

1.2 地下水数值模型

因研究区所在的水文地质单元范围较大，结合数据及资料情况，模拟区范围南界和北界分别以1 340 m和1 500 m等高线为界，东界为兵团农场水库和干渠，西界垂直于地下水水位埋深等值线，面积约412 km2。模拟区的东侧、北侧和南侧均概化为水头边界，西侧为零流量边界；胜利干渠和兵团农场干渠为一混合边界，在灌溉期间，接受干渠的渗漏补给，非灌溉期为零流量边界。垂向上接受大气降水的入渗补给及水面蒸发，模拟区范围及边界条件如图2所示。

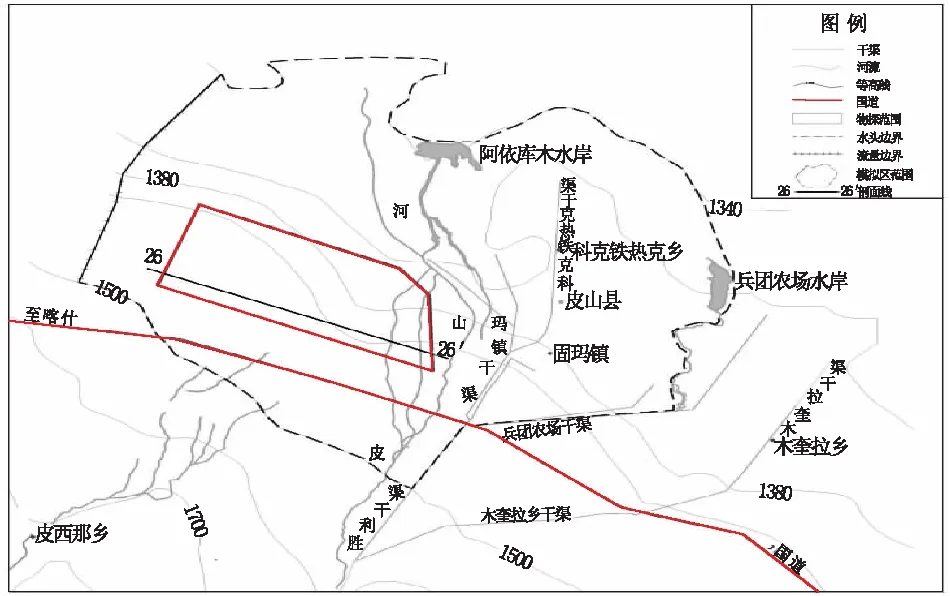
图2 模拟区范围及边界条件

根据水文地质概念模型，将模拟区地下水流概化成非均质各向同性非稳定二维地下水流系统，并建立相应的数学模型。

(1)

式中：K为含水层的渗透系数(m/d)；h为地下水水位(m)；z为潜水含水层底板(m)；W为单位体积流量，用以代表流进源或流出汇的水量；μ为给水度；H0为初始水位(m)；t为时间(d)；D为模拟区范围；Γ1为一类边界；Γ2为二类边界；q为含水层侧向单宽补排量(m2/ d)，隔水边界为零。

2 灵敏度分析

灵敏度分析可以对模型中参数的不确定性对模型的输出结果的影响程度进行评价与量化。故而，在地下水数值模型中，参数灵敏度分析是必不可少的[6]。

参数灵敏度分析主要包括局部灵敏度分析与全局灵敏度分析[7-8]。局部灵敏度分析是用来分析单个参数变化对数值模型输出结果的影响程度，不考虑参数之间的耦合作用。从数学角度来说 ，在某设计点Xk 处某个设计函数 Fj(X)对设计变量xi的灵敏度可由式(2)计算得到[9]：

(2)

其中|Sji|为函数Fj(X)对Xi的灵敏程度，其值越大，则说明灵敏度越大，对数值模型的影响程度也就越大。

根据式(2)并结合当地资料，本次数值模型中选用的参数包括渗透系数(K)和给水度(S)，以及刻画边界条件的水力传导系数(C)。首先对渗透系数K进行灵敏度分析。保持其他两个参数数值不变，将K值变化依次 ±10%、±20%、±30%，每改变一次K值，记录一次对应的地下水位变幅，其他参数的灵敏度分析同理，得到参数局部灵敏度分析结果如图3所示。

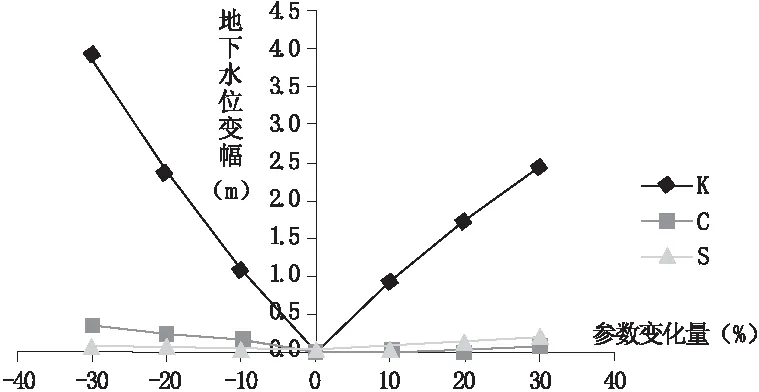
图3 局部灵敏度分析结果

由图3可知，不论参数增大还是减小，渗透系数 K值对模型地下水位影响最大，即K值的灵敏度最高。例如当参数变化均为-10%时，渗透系数K、水力传导系数C、给水度S变化引起的地下水位变幅分别为-1.083 m、-0.155 m、-0.037 m。此外当参数变幅为负值，即参数值减小时，C较S灵敏度更高，变幅为正时，S较C的灵敏度偏大，但因对数值模型得到的水位值的影响程度均较小。由于该研究区地下水数学模型是非线性模型，因此参数增大和减小相同百分比时，图像并不是关于y轴完全对称，即参数增大和减小相同百分比时，对模型的影响并不完全相同，这也间接反映出参数的变化幅度对水位输出结果的影响并不是线性变化的。

局部灵敏度分析方法操作简便，但未考虑参数之间的相关性及相互影响的作用，以及参数之间会相互影响继而影响数值模型的输出结果。而全局灵敏度分析方法可以考虑多个参数之间的耦合影响，因此可以弥补局部灵敏度分析方法的不足。

根据局部灵敏度分析选取的三个参数进行组合，得到KS、KC、SC、KSC四种组合形式，并依次同时变化±10%、±20%、±30%，分别运行相应的数值模型得到变化后的地下水水位变幅，结果如图4所示。

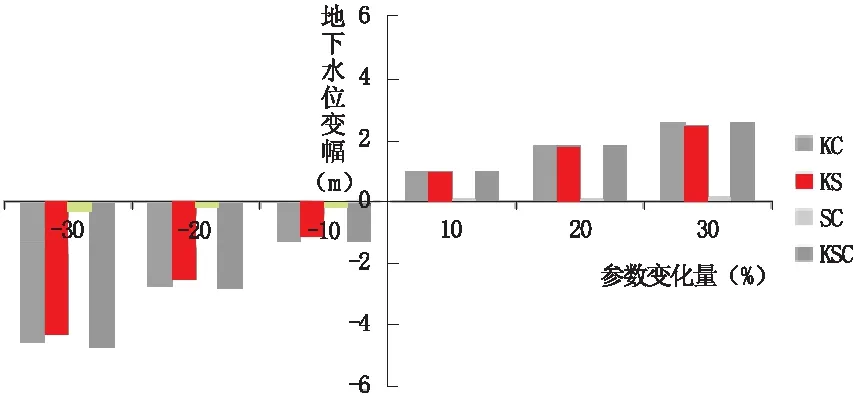
图4 参数全局灵敏度分析

由图4可知，三个参数KSC同时变化时，对模型输出结果影响最大，与数值模型的理论分析结果相一致，KC、KS、SC组合对模型水位输出结果影响幅度相应的有所降低。例如，当参数组合均减小10%，KSC引起的地下水位变幅为1.315 m，而KC、KS、SC引起的地下水位变幅分别为1.301 m、1.146 m、0.156 m，均小于1.315 m。

将局部灵敏度分析结果与全局灵敏度分析结果对比，K单独变化+10%时，地下水变幅为0.925 m，K分别与S、C的参数组合KS、KC引起的地下水位变幅为0.958 m、0.939 m，由K单独引起的变化量分别占到96.56%和98.55%。K单独变化-30%时，地下水位变幅为-3.913 m，KS、KC引起的地下水位变幅为-4.339 m、-4.593 m，此时，由K单独引起的变化量分别占到90.18%和85.19%。由此可以看出，该研究区地下水数值模型灵敏度最大的参数是K，但同时也应注意到，在变幅较小时，K的变化量在参数组合中占比极大(96%以上)，变幅增大时，K的变化量虽然仍旧占据绝大部分(85%以上)，但是其比例有所下降。因此，在实际应用中，如果对数值模型的输出精度要求较高，则需重点考虑渗透系数K和C的变化及资料丰富程度，反之，如果对模型输出结果精度要求不高，考虑到人力、物力、财力等因素的影响，其他灵敏度较低的参数对模型的影响可暂不考虑。

由上分析可知，全局灵敏度分析与局部灵敏度分析结果类似，渗透系数K值的影响最大，由于全局灵敏度分析考虑了各个参数之间的耦合作用，因此更加贴近实际。对参数进行灵敏度分析，可以使地下水数值模型更加完善，更好服务生产生活。

3 结语

本文通过对新疆皮山县塔克拉玛干沙漠南缘的绿洲建立数值模拟模型，围绕数值模型中的参数进行局部和全局灵敏度分析，得出在所选的三个参数含水层渗透系数K、给水度S、水力传导系数C中，含水层渗透系数K的灵敏度最高，给水度S次之，C影响不明显。其排序为|K|>|S|>|C|。全局灵敏度分析可以考虑各个参数之间的相互关系对地下水数值模型输出结果的影响，较局部灵敏度分析方法更贴合实际。对参数进行灵敏度分析，可以得出对所构建的地下水数值模型影响最大的参数，在构建模型以及率定相关参数等方面可以重点关注，为决策者做出更加合理的决策提供依据。