基于三阶段DEA模型的创新效率实证研究——来自2005年到2020年全国工业企业的证据

陈 池

1 引 言

工业是国民经济的主导产业，是国民经济的重要构成部分，研究其创新效率的实况，不但可以为改进自身的创新效率提供了现实的依据，而且为其他类型企业的技术创新提供了很好的借鉴作用。工业企业经过70多年来的发展，不断壮大，2020年工业总产值占国内生产总值的30.8%，成为我国重要的经济力量（国家统计局，2021［1］）。我国的工业从纯粹依靠技术引进，发展到引进与消化吸收相结合，然后不断创新和加强正向设计能力，在新经济常态下积累到原始技术的创新（钟顺东，2017［2］），工业科技创新的发展从一定程度上决定了一个国家的经济增长能力，到目前为止，中国工业已形成了别具特色的技术赶超路径。综观工业技术发展历史来看，1949-1977年，中国工业技术创新主要是依靠技术援助和归国科学家的艰苦探索中前行；1978-1991年，我国以技术引进和外商直投为主；1992-2005年，自邓小平同志1992年南巡后，从单纯技术模仿发展到不断增强自主研发能力，各项技术资源也向企业集中；2006年之后，工业企业经过多年研发经验和积累，创新能力有了质的提升。根据统计数据表明，全国规模以上工业企业2020年的专利申请数是2005年的21.5倍，16年的年平均增长率为23.1%；新产品销售收入也是逐年增加，2020年的新产品销售收入是2005年新产品销售收入的8.9倍，16年的年平均增长率为16.5%；大部分的工业企业知识产权意识明显提升，研发效率也是突飞猛进，以更多的新产品、新技术作为开拓和占领市场的有力武器，体现了极强的生命力。

在同一时期，通过加强国家产业转型升级和技术创新政策的引导，激励了工业企业的自主创新，各项经费支出和研发人员投入也增强了，2005年以来，工业企业的研发经费和研发人员投入都呈现持续增加的趋势。与2005年的R&D经费相比，2020年是2005年的11.2倍，年平均增长率为18.2%；2020年的R&D人员全时当量是2005年的4.7倍，年平均增长率为12.3%。研发经费投入和研发人员增长表明企业越来越重视原始创新能力的提升，通过对16年的创新成果的统计分析，工业企业的创新能力无论是数量还是质量上都有了明显的提升。国内外众多专家学者关于工业企业创新效率的研究很多,他们的研究成果对本文具有很重要的借鉴意义，但可能源于研究视角和方法的限制，以往研究在考察企业技术创新的效率时，并没有将环境因素和随机误差予以剔除，所以效率值并不能反映我国现阶段工业企业技术创新的真实效率水平。

本文将根据规模以上工业企业16年的研发投入和产出数据，参考马占新等（2013）［3］DEA三阶段方法对其创新效率进行了各年份的对比，由于各年份的经营环境的不同，对企业的创新效率的影响也不一样。本文旨在建立合理的评价方法和指标，客观评价工业企业的创新效率，并针对存在的问题提出相关对策,以促进该产业的高速持续增长。本文提出的三阶段DEA 模型方法，在有效控制环境因素和随机误差的基础上，对我国工业企业的技术创新效率水平进行科学评估，并分析影响其创新效率的因素，为相关部门决策提供参考。

2 文献综述

目前，大多数学者采取参数方法和非参数方法对高技术产业的创新效率进行评价。其中，参数方法主要是基于随机前沿分析（SFA）进行评价，但是它在设置函数模型时会存在一定的偏差;非参数方法主要是基于数据包络分析（DEA）进行评价，相比于SFA模型更加客观。DEA模型最早是由Charnes等提出的，是基于规模报酬不变的假设衡量各个决策单元的效率（CCR模型）;后来学术领域基于此衍生出几十种模型。龙勇等采用CCR和C2GS2模型分析我国高技术产业1995-2002年的效率，解垩采用CCR和Malmquist-DEA模型分析了我国高技术产业五个行业1997-2004年的效率，这些都是对其进行单阶段分析。

熊彼特认为技术创新作为一种因素构建了新的生产函数，成为影响企业及经济发展的重要因素，熊彼特之后，随着学者专家对技术创新的研究与发展，对技术创新绩效（或者效率）的研究，经历了两个阶段：第一阶段是单要素生产率,是指企业的产出水平与投入要素中某一单独的要素之间的比例，研究的是单一生产要素对绩效的贡献程度，但是事物之间的联系非常广泛，各种生产要素之间也是有着千丝万缕的联系，而创新效率往往多种生产因素共同作用的结果，所以单一要素生产率具有一定的局限性，不能全面解释企业真实的经营状况。第二阶段是全要素生产率，全要素生产率可以揭示生产技术水平的高低，也揭示生产效率的高低，全要素生产率的提高路径包括技术进步以及生产要素的重新配置，即使是完全相同数量和质量的研发资金、研发人员等生产要素投入，其产出量（包括专利数量或者新产品销售收入等）也不一定相同，究其原因关键在于全要素生产率的不同。本文将沿着全要素生产率这一个思路，运用多种投入和多种产出因素，揭示各因素之间的投入与产出关系。

分析工业企业的创新效率，由于角度及方法的不同，会得出不同的分析结论，以下是主要的专家学者的观点及研究方法：蒋玉洁和菅利荣（2011）［4］运用熵权TOPSIS方法和锡尔指数，分析了我国不同区域的工业企业创新发展水平及差异性；赵良浩等（2013）［5］用回归法验证了不同的科技创新政策对创新绩效的不同影响；申文青（2019）［6］，运用灰色关联分析法，对广东省制造业的技术创新绩效进行了综合评价；鲁炜等（2014）［7］利用Eviews6.0 软件，以上市公司的财务数据分析了资本结构对创新的影响；朱孟涛（2013）［8］利用DEA模型分析了各区域30个省市及地区的工业企业的创新效率并进行了评价；陈艺曦，于博骏（2019）［9］运用K-means 算法，经过聚类分析及因子分析提取了影响创新能力的因子，并对各地区工业企业的创新能力进行了评价；王翔（2019）［10］运用SYS-GMM方法实证分析了环境规制对创新的影响；何田和胡笑寒（2018）［11］采用DEA分析方法,评价了大中型工业企业的技术创新效率，发现创新活动不足，地区的差异性明显，投入的要素资源被浪费等等；胡艳和刘梅林（2018）［12］利用DEA和DEA-Malmquist 指数法，分析了安徽省工业企业动静态的创新效率；陈娜等（2019）［13］采用DEATobit模型，对西部地区工业企业的创新效率进行了评价；罗芳和王远卓（2019）［14］运用DEA方法，分析了长江经济带规模以上工业企业的研发效率；姜波（2012）［15］以非参数Malmquist 指数方法实证分析了30个省区域大中型企业的技术绩效差异性。

3 数据来源和变量

本文主要采用DEA模型分成三个阶段进行分析，第一阶段DEA模型，主要采用收集到的工业企业的原始的投入和产出数据进行初始效率的分析，得出不同投入的松驰变量；然后进行第二阶段分析，以SFA回归方法以排除环境因素和统计误差的影响；最后第三阶段以调整后的不同投入的调整变量为基础，得出了在同质的条件下的真实技术效率值。

（1）数据来源

2005年到2020年的投入和产出的数据主要来源于《工业企业科技活动统计年鉴》［16］和《中国统计年鉴》，鉴于不同的年鉴统计口径会略有不同，年份统计数据可能会出现差异性，导致有的年份的数据出现断层现象，在剔除了不连续的数据后，作者收集整理了2005到2020年的经营数据，作为本文实证分析的基础数据。

（2）投入、产出变量

本文研究的是工业企业的创新绩效，与科技投入密切相关的是R&D人员全时当量和R&D经费两个变量。研发人员是工业企业研发主力，数量大小体现了研发力量的规模。研发经费则体现了工业企业对技术创新投入的资金力量的大小，也体现了企业对研发工作的重视程度。

在产出方面，由于研发的最终成果体现在专利数量的多少，研发成果多，则专利申请数量就会增加；而新产品体现了研发成果的转化为产品的重要标志，如果申请的专利不能顺利被企业转化为产品，则表明企业的研发成果的转化程度比较低，事实上也有一部分的专利仅仅是作为研发成果的体现，并不能转化成生产力。所以本文选取了专利申请数和新产品销售收入共同作为研发产出的衡量指标。

（3）环境变量

为了得出创新效率的真实情况，需要排除环境及统计因素的影响，所以要选取不在样本主观控制范围之内的环境因素，与本文选取的投入变量进行回归分析，经过收集、整理和试测试效果，选取了三个符合要求的环境变量，具体包括反映科技开发绩效的科技成果登记数［17］、反映总的投资规模的全社会固定资产投资［18］和反映企业缴纳税收规模的企业所得税［19］，由于这三个变量不受管理控制的约束,并且可以满足三阶段DEA模型的分离假设。

4 实证分析

本文运用DEA模型分三个不同的阶断进行实证分析，第一阶段采用原始的投入和产出数据运用DEAP2.1软件进行数据运算，第二阶段主要是采用Frontier4.1软件［20］进行数据处理，第三阶段投入的数据有所区别，产出数据相同，投入数据是采用第二阶段运算所得的调整数据，有关的实证分析过程具体如下：

4.1 相关性分析

为进一步判断本文所采用的投入与产出变量的适当性和有效性，首先运用SPSS软件进行相关性分析，对专利申请数、新产品销售收入、R&D经费、R&D人员全时当量四个投入和产出变量进行相关性分析，结果如下图（图1），投入、产出，4个变量之间在0.01级别（双尾），相关性显著，可以作为本文进行分析的数据。

4.2 第一阶段创新效率分析

首先对所收集到的原始值进行运算分析，没有剔除任何内外部因素的影响，反映了初始状况的效率值，通过2005-2020年规模以上工业企业的研发投入和研发产出绩效进行分析，得出了16年的三种技术效率值及技术效率值的平均值，计算结果如表1所示。从表1 中可以看出，平均综合技术效率、平均纯技术效率、平均规模效率分别为0.972、0.979和0.993，三种技术效率值比较接近且处于高位。从表1还可以看出来，综合技术效率低于平均值的有2012年-2015年、2018年，余下的年份都大于平均值，处于优良状态；综合技术效率值为1的年份是2007年、2008年，2017年、2020年，4年DEA有效；纯技术效率低于平均值的有2012年-2015年、2018年，余下的年份都大于平均值，纯技术效率值为1的年份是2005年-2008年、2010年，2017年、2020年，7年DEA有效；规模效率低于平均值的有2006年、2010年、2011年、2013-2016年，余下的年份都大于或等于平均值，规模效率值为1的年份是2007年、2008年、2017年、2020年，4年DEA有效；纯技术效率达到DEA有效而综合技术效率没有达到DEA有效的年份为2005年、2006年、2010年，主要的原因是其规模效率无效,因而需要重点研究如何更好地提升其规模效率。

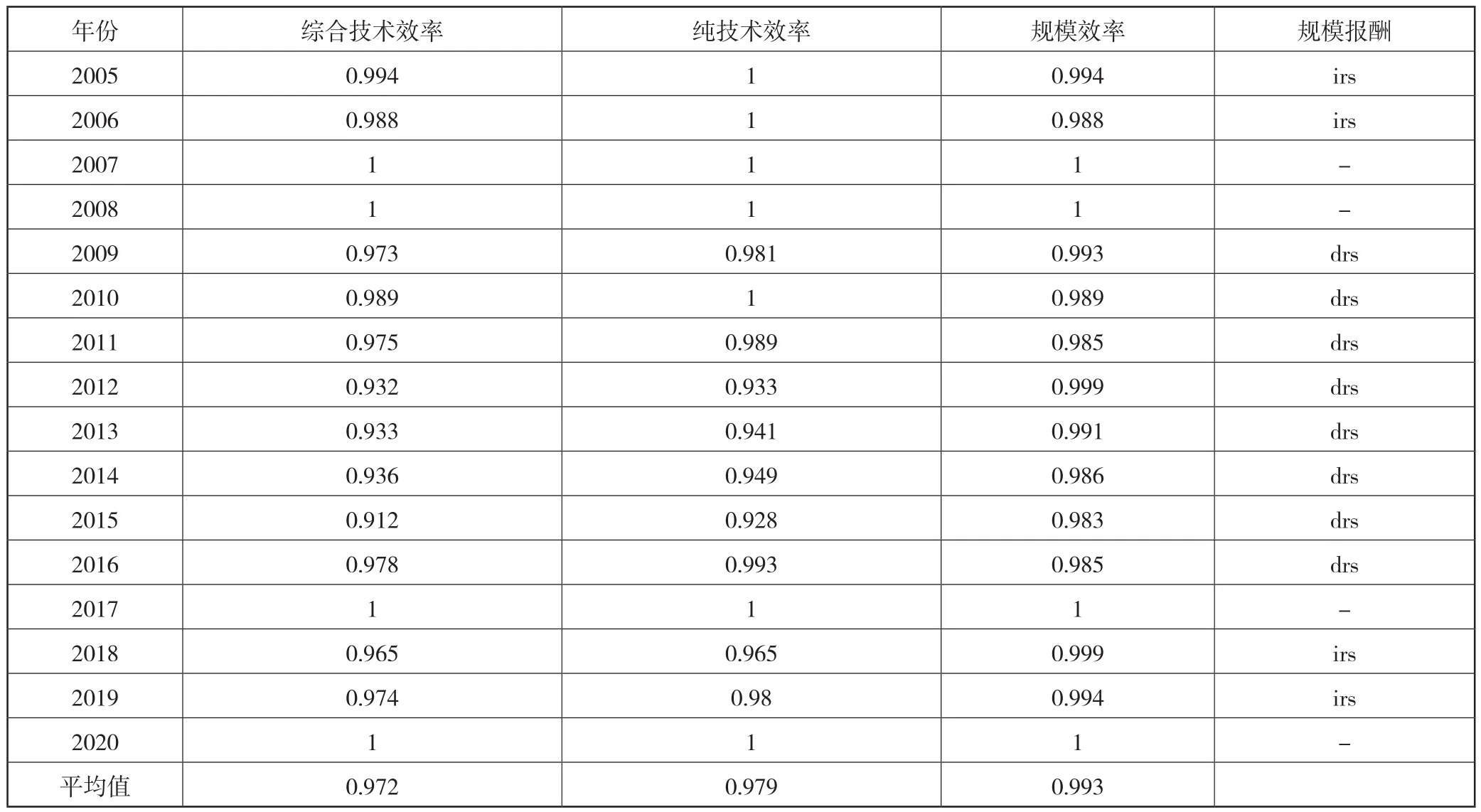
表1 第一阶段效果系数

从三种效率发展趋势图（见图2）可见，发展趋势比较平衡的是规模效率，主要是在0.98到1之间波动，而综合技术效率和纯技术效率的运行轨迹基本相似，从形态上来看波动比较大，从2008年的最大值不断波动下降到了2015年最小值，然后不断提升，到2020年重新达到最大值。结合宏观的经济发展情况，我们对技术效率的发展情况深入进行剖析，究其原因，与国内外的经济形势密不可分，主要的原因是从2012年到2015年期间，存在的问题比较突出的来自投资和需求不足，经济波动加剧等等；2015年后随着国家加强了宏观调控政策，技术效率也进入了稳定增长状态，深化改革进入发力期，伴随着经济发展形势的不断好转，工业企业的技术效率也在不断提升，到2020年，重新达到最大值，DEA有效。

4.3 第二阶段创新效率分析

由第一阶段利用DEAP2.1软件进行运算后，用R&D经费和R&D人员全时当量的原始值减去目标值后，分别得出这两个变量的松驰变量值，为考察本文中所选取的三个环境变量对投入松驰变量的影响程度，分别以这两个不同的投入变量为因变量，环境变量作为自变量，运用Frontier4.1软件进行回归分析，具体情况见表2，可以看出, 两个投入松驰变量回归后的GAMMA值均达到了1，表明管理效率无效是主要的影响因素，从结果中可以看出，LR 单边检测是通过了显著性检验，其中投入1（R&D经费）通过了10%的显著性检验；投入2（R&D人员全时当量）通过5%的显著性检验。因此, 所选用Frontier4.1分析是合适的。

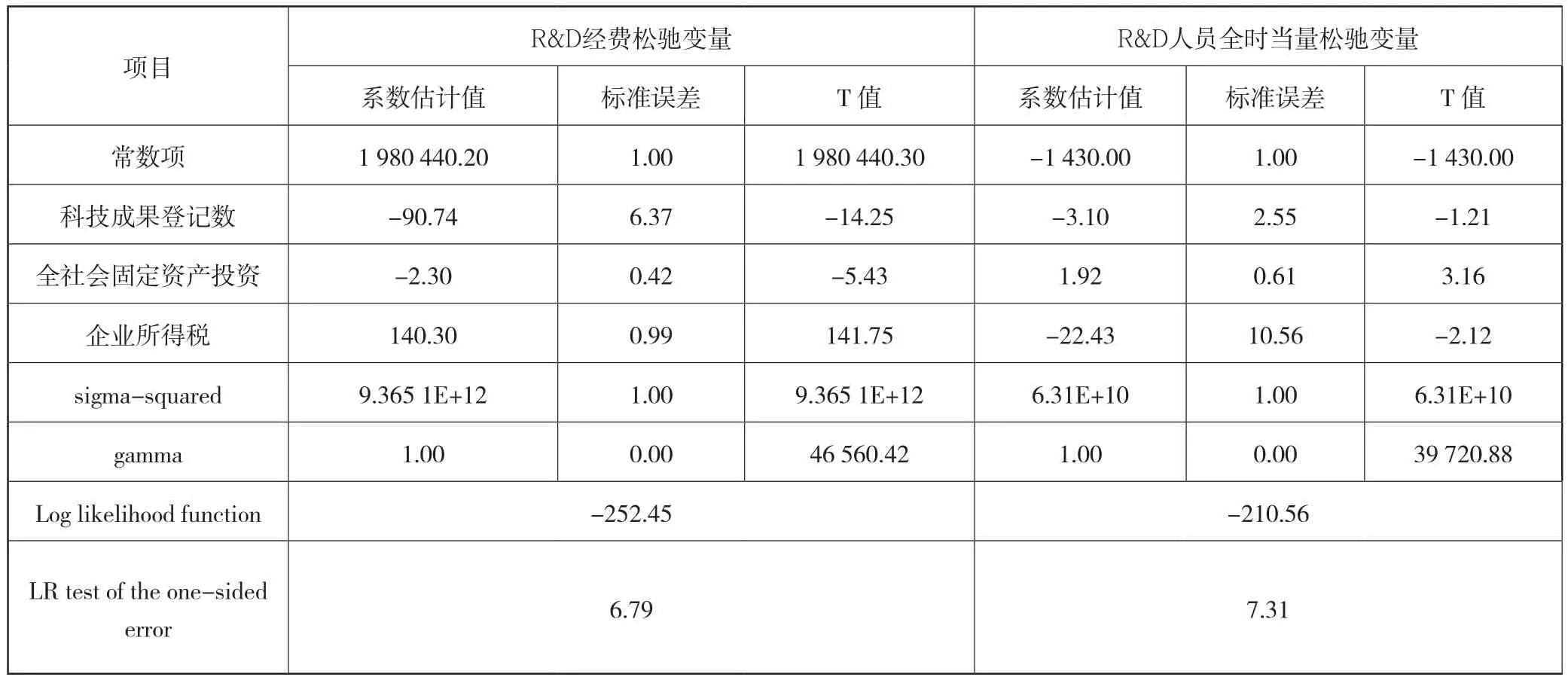
表2 第二阶段SFA估计结果

（1）科技成果登记数

科技成果登记数的增加对于R&D经费和R&D人员全时当量来讲都是有利因素，会带来R&D经费松驰变量和R&D人员全时当量松驰变量的减少，估计的原因有可能是，随着全社会的科技成果登记数的增加，激发了工业企业对研发的热情，不断增加研发经费和研发人员，进一步提高了研发效率，所以得到了更好的研发成果，但科技成果登记数的增加对于R&D经费和R&D人员全时当量这两个变量的影响程度不一样，每增加一个单位的科技成果登记数对R&D经费松驰变量的影响是R&D人员全时当量的29.3倍。

（2）全社会固定资产投资

由于全社会固定资产投资的增加也相应减少了R&D经费松驰变量，属于有利因素，可能的原因是，由于全社会固定资产投资的增加相应减少了企业研发经费的支出，减轻了企业的负担；而另外一方面，对R&D人员全时当量来讲是不利因素，带来了R&D人员全时当量松驰变量的增加，全社会固定资产投资的增加对这两个变量的影响程度不一样，对前者的影响是后者的1.2倍,并且方向相反。

（3）企业所得税

企业所得税增加对于R&D经费来讲属于不利因素, 会增加相应的R&D经费松驰变量，这可能由于随着企业所得税的增加，增加了企业的成本负担，导致松驰变量的增加；对于R&D人员全时当量来讲是有利因素，企业所得税增加相应减少了R&D人员全时当量松驰变量，企业所得税每增加一个单位，对R&D经费的影响是R&D人员全时当量的6.3倍，但方向相反。

总体上来讲，从统计数据来看，环境变量对松驰变量的影响远大于统计误差的影响，排除环境因素和统计因素对创新绩效的影响后，政府或者企业可以根据各年份的真实创新绩效情况，对原始投入变量进行适当的调整。

4.4 第三阶段创新效率分析

运用Frontier4.1软件经过第二阶段运算后，得出了R&D经费和R&D人员全时当量这两个投入变量的调整后的变量值，再把原始的产出变量和调整后的投入变量进行运算, 可获得排除外部影响因素的第三阶段效率值，从表3中可以看出，在同质环境下，与第一阶段效率值相比较,平均纯技术效率保持不变，平均综合技术效率和平均规模效率略有下降，变化不大，分别下降了0.1%和0.1%。总体上来看，对三种效率（综合技术效率、纯技术效率和规模效率）的平均值影响不大，但是对于2005年到2020年每一年的具体技术效率数值影响较大。

表3 第三阶段效率值分析表

续表

为了进一步对比第三阶段和第一阶段效率值的变化情况，现将综合技术效率、纯技术效率和规模效率的每一个年度的第三阶段和第一阶段的具体数值进行比较，详见图3、图4和图5。从三幅雷达图中可以看出来，第三阶段的纯技术效率和第一阶段的具体值基本一致，差别最大的是规模效率，综合技术效率变化程度处于纯技术效率和规模效率之间。下面以规模效率来进行详细说明，2007年、2008年、2012年、2014年、2017年和2020年这六年的第三、一阶段的规模效率是相等的；2009年、2010年、2015年、2016年、2018年和2019年的第三阶段规模效率值上升了，而2005年、2006年、2011年和2013年的第三阶段规模效率值下降了，其中变动最大的是2005年，减少了0.023。

5 结论和建议

本文研究的三阶段DEA 模型，其研究思路是首先利用经典的模型测算决策单元的效率水平，然后利用随机前沿模型对投入变量进行修正，使各个决策单元处于相同的环境当中，最后利用修正后的投入数据重新测算决策单元的效率值。由于该方法有效剥离了环境因素和随机误差的影响，因而测算结果也更接近真实的效率水平。同时本文运用三阶段DEA 模型进行实证研究，以全国规模以上工业企业为研究对象，经过不同阶段效率值的大小和变动趋势的对比分析，我们可以得出如下结论，并提出相应的建议：

（1）全国工业企业的创新效率水平较高，三种技术效率的平均值都在0.97以上，接近DEA有效，但是仍然存在改善的空间。以第三阶段的纯技术效率情况来看，7年的纯技术效率达到DEA有效，占比为43.8%，将近一半；而其中2年的纯技术效率达到DEA有效，但是综合技术效率没有达到DEA有效，这是由于这两年规模效率偏低，导致综合技术效率也没有达到最优。从技术资源的使用情况来看，全国工业企业对投入资源的利用情况，接近DEA有效，关键的是需要进一步研究规模效率的情况，综合分析各种投入和产出的协调问题，改善工业企业的规模效率，通过规模效率的提升从而提升综合技术效率值，最终看能否达到综合技术效率DEA有效。

（2）加强治理，减轻环境因素对全国工业企业的创新效率的影响。在剔除环境因素的影响后，通过对比全国工业企业第三和第一阶段的创新效率，发现平均综合技术效率和平均规模效率轻微下降，而平均纯技术效率保持不变，表明对总体的平均值影响不大，但是对于每一年度的三大创新效率值有显著影响。结合第二阶段的SFA实证分析，发现随着科技成果登记数的增加，可以适当减少R&D经费和R&D人员全时当量的松驰变量，政府首先需要在软环境方面加以努力，如加强知识产权保护，保护技术和专利收益，激励工业企业提高技术人员和资金的投入，提升创新的意愿和能力；全社会固定资产投资的增加，有利于R&D经费松驰变量的减少，却带来R&D人员松驰变量的增加，建议在增加固定资产投资的同时，需要配套好研发经费投入的幅度和结构，并对研发资金的使用效率进行监控，制订有利于激励研发人员投入研发的福利措施等等，双管齐下助力工业企业创新效率的提升；企业所得税增加带来R&D经费松驰变量的增加，却减少了R&D人员全时当量松驰变量，企业所得税对于企业研发经费影响较大，所以在制订企业所得税政策时，需要考虑如何在税制方面支持企业自主创新的提升，如加大对企业自主创新投入的所得税前抵扣力度，实施更加优惠的税收政策等等。

（3）解决投入不足和冗余的问题，提升全国工业企业规模报酬效率。根据第三阶段效果系数显示，从2005到2020年共16年中，全国工业企业达到规模有效的共有6年，3年（2005年、2006年和2019年）是规模递增，存在投入不足的问题；7年（2009年、2011年到2016年）是规模递减，存在投入冗余问题，需要加强投入要素的治理。工业企业需要进一步加大研发的资金投入，同时发挥财税金融政策作用，加大政府研发资金的支持，激励企业创新活动的开展；可以考虑大力发展融资租赁业，支持工业企业的设备更新和技术改造；加强对研发、新产品形成和销售全过程的监控，在保质保量的前提下加强成本管理，提高研发绩效；规模不当已成为制约全国工业企业投入产出效率的关键，要进一步深化研究投入产出协调发展的问题，既要注重技术提升又要兼顾合适的规模发展，解决规模过大或者过小的规模不经济难题。

（4）加强工业企业的内部运营和管理水平，促进技术效率的提升。根据本文三阶段的DEA分析，运用GAMMA变差率进行检验，变差率的取值范围是（0，1］，经过回归得出R&D经费和研发人员全时当量的投入变量的GAMMA值为1，说明效率偏差主要由管理无效率项决定,随机误差的影响可以忽略不计。工业企业需要加强企业技术引进、消化、吸收和二次创新的全过程技术管理，提升技术创新效率；强化对工业企业研发资源的配置和利用，研究生产要素投入的合理比例，增加产出价值，组合成一定的批量生产能力，促使各项费用节约，生产成本降低，进一步扩大规模效益；对于创新效率低的国有工业企业，可以考虑逐步引入民营资本，通过改制的方式激活创新的动力，提升创新效率；积极利用信息化和智能化等先进技术促进技术创新，并且整合企业、科研机构和高校的技术研发力量，提升企业的技术研发和创新能力等等。