“双碳”背景下光伏建筑一体化发展前景

文/刘恋平，刘虹霓

将股票的移动平均值乘以各自权重与基准日市值k的比值再乘100得出板块指数，从而计算出板块指数的移动平均线。在这些数据的基础上使用未经处理的ARIMA模型对板块指数移动平均线进行预测。由于未经处理的ARIMA模型误差较大，又对ARIMA模型中的（p，d，q）进行修正，得出准确的ARIMA模型。本文对上证指数和光伏建筑一体化板块指数利用Eviews软件进行相关性分析。

我国用能和碳排放形势严峻，“碳达峰”与“碳中和”成为国家与社会关注的重要议题。[1]光伏产业作为一种节能的新能源产业运用在建筑行业中，成为一种良好发展的趋势，与之相关的股票也有不断上涨的趋势。本文通过对历史数据的运算，从大体上给出该板块的发展趋势。

本文对37家光伏建筑一体化相关企业的股票数据进行分析，将南玻A在1992年2月28日的收盘价k作为基准日市值，当前市值由各股票的收盘价与各股票的权重相乘再累加得到，通过给出的计算公式求解板块指数。要得出光伏建筑一体化板块指数的移动平均线，就需要计算出光伏建筑一体化板块指数各个时间段的移动平均值，建立板块指数移动平均值求解模型。根据2021年光伏建筑一体化板块指数五日的移动平均线，建立ARIMA模型，预测出2021年5月6日至5月28日数据。在没有做任何处理的情况下，ARIMA模型预测出来的数据存在较大的误差。在进行一定的修正得到准确的ARIMA模型后，修正的模型预测该板块指数5月28日后20个交易日的日移动平均线、3周的周移动平均线、2个月的月移动平均线。利用2019年4月1日至2021年5月28日各只股票的收盘价、成交量计算出光伏建筑一体化板块指数以两个月为周期的各个时间段的移动平均值。利用2019年4月1日至2021年5月28日上证指数的数据，以两个月为周期计算出各个时间段移动平均值。最后对计算出上证指数和光伏建筑一体化板块指数各个时间段的移动平均值数据利用Eviews软件做相关性分析。

一、移动平均线模型的确定

要得出光伏建筑一体化板块指数的移动平均线，就需要计算出光伏建筑一体化板块指数各个时间段的移动平均值，可以根据计算各个时间段各只股票的移动平均值乘以它们各自的权重与基准日市值k的比值再乘100得出。公式如下：

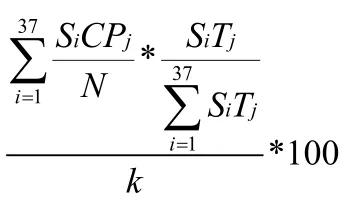
式中，SiTj表示第i只股票第j个时间段的成交总量；SiCPj表示第i只股票第j个时间段的收盘价；N表示以N天为一周期，可取5、10、20。

二、ARIMA模型的建立

（一)时间序列ARIMA模型的建立

ARIMA方法的基本理念是,要预测的时间序列是由某个随机过程生成的,进而可以利用过去的观测值来推出未来的序列值。[2]考虑到板块指数的移动平均值数据通常是缺乏平稳性的，因此对其进行一阶差分处理，使数据保持平稳性，接着建立AR（自回归模型)。p阶回归公式如下：

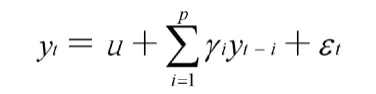
式中，yt为当前值；u为常数项；p为阶数；γi为自相关系数；εt为误差。

MR（移动平均模型)公式如下：

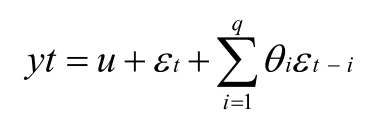
自回归模型AR和移动平均模型MA模型相结合，就可得到自回归移动平均模型ARMA(p,q)，计算公式如下：

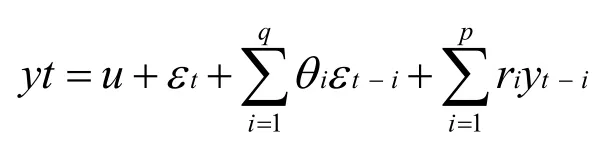
将自回归模型、移动平均模型和差分法结合，就可得到差分自回归移动平均模型ARIMA(p,d,q)，其中d是需要对数据进行差分的阶数。

（二)ARIMA模型中p、d、q建立

1.d的确定

没有做差分的数据不平稳，经过一阶差分处理过的数据变得平稳，故确定d＝1。

2.p、q的确定

由PYTHON程序画出ACF、PACF图，如图1、图2所示：

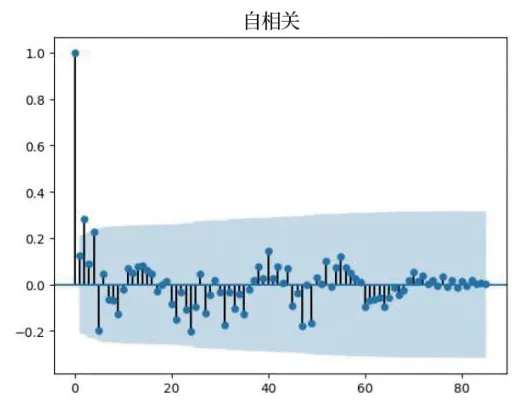
图1 ACF图

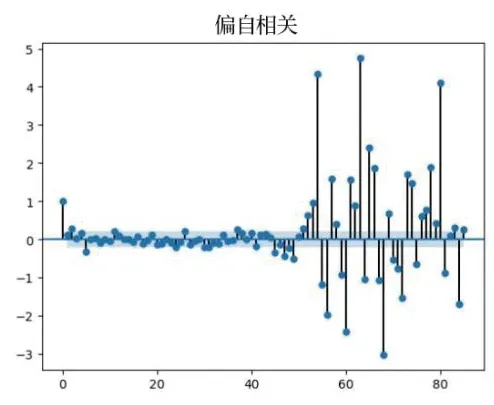
图2 PACF图

可以看出，p＝0,q＝1，因此确定模型为ARIMA（p＝0,d＝1,q＝1)。通过此模型预测2021年5月6日至5月28日数据图像，如图3所示。

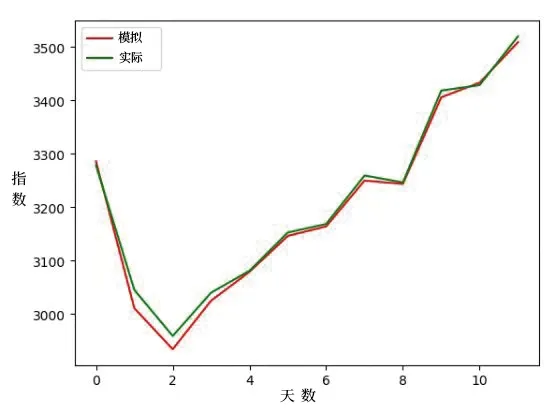
图3 2021年5月6日至5月28日板块指数的MA5预测和实际值

三、上证指数和光伏建筑一体化板块指数的相关性分析

（一)上证指数和光伏建筑一体化板块指数数据之间线性相关的判断

在Eviews中，通过输入上证指数和光伏建筑一体化板块指数，把光伏建筑一体化板块指数当作解释变量，设为x；上证指数当作被解释变量，设为y。通过plot操作，由趋势图观察出经济变量x、y的发展趋势大体都是增长的，但是存在异常值，两变量之间的关系不明显。

再画出回归线去检验x、y的线性相关性，根据相关图，大多数点都没有落在回归线上，因此基本判断x、y变量相关类型应该是非线性的曲线相关关系。接着初步将模型设定为双对数函数模型、对数函数模型、指数函数模型和二次函数模型，并分别从以下四个方面考虑并估计出准确的模型：

（1)回归系数的符号、值的大小；

（2)改变模型形式之后是否使判定系数的值明显；

（3)各个解释变量t检验的显著性(是否能通过)；

（4)系数的估计误差较小。

（二)模型的选择

在Eviews命令窗口中键入命令来估计模型，选择二次函数模型、双对数函数模型、对数函数模型、指数函数模型。通过Eviews比较以上模型可见，除二次函数模型中x^2的回归系数为负数，与实际情况存在一定的偏差外，其他模型回归系数的符号及数值较为合理，因此我们舍去二次函数模型。另外，双对数函数模型、对数函数模型、指数函数模型的解释变量及常数项都通过了t检验，模型都较为显著。除了指数模型的拟合优度较低外，其余模型都具有高拟合优度，因此可以首先剔除指数模型。再检验双对数函数模型、对数函数模型、指数函数模型的残差，这三种模型的残差在较长时期内呈连续递减趋势又递增，然后又转为连续递减又递增的趋势。而通过残差图比较得出，双对数模型和指数模型的残差落在虚线框里的比对数模型的要少，可以初步判断双对数函数和指数函数形式设置是不当的。另外，这两个模型的拟合优度也较对数模型低，所以可舍弃双对数模型和指数模型，选择对数函数模型。

（三)模型的确定

最终确定模型为对数模型，方程如下：

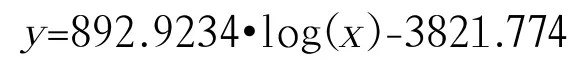
通过Eviews得出y,log(x)的相关性是0.951565，是比较高的，模型是合理的。

四、结语

面向“碳中和”目标的低碳转型，将对社会经济系统和自然系统产生深远的影响。[3]而建筑领域一直是碳排放大户，在国家“碳达峰”和“碳中和”的远景目标指引下，光伏建筑一体化具有广阔的发展前景。

板块指数是将同一板块的个股按不同的权重方式生成的相关指数，是对各板块走势的整体反映。通过对37家光伏建筑一体化相关企业的股票数据对光伏建筑一体化板块指数的分析与预测，由绘制出的板块指数移动平均线，我们可以看出，2019年4月1日 至2021年4月30日，板块指数一直处于相对稳定的动态变化之中；在交易天数约为200天的时间点，出现了板块指数的一个小高峰，在这一时间段内，板块指数虽然有所增长，但变化不大；在这个时间点往后的一段时间内，大约进入2020年，板块指数处于动态变化中，但呈现出爆发式上升的趋势；在交易天数约为430天的时间点，大约在2020年9月，出现了板块指数的最高点。