选区激光熔化梯度多孔支架力学性能和能量吸收研究
2022-10-18曾寿金李传生许明三李涤尘
曾寿金 李传生 刘 广 许明三 李涤尘
1.福建工程学院机械与汽车工程学院,福州,3501182.西安交通大学机械制造系统工程国家重点实验室,西安,710049
0 引言
基于孔径、孔隙形态及孔隙率优化分布的梯度多孔结构因其具有足够的强度、优异的能量吸收特性,以及在特定区域承载不同力学性能的能力而受到越来越多的关注[1-3]。在股骨和胫骨的医学修复中,由于骨骼与骨支架之间的弹性模量存在较大的不匹配性,从而导致“应力屏蔽”效应,常常需要将医用金属支架设计成多孔结构,以降低其弹性模量,实现个性化定制。而人体股骨、胫骨等天然骨都是梯度多孔结构,其孔隙率从边缘到中心逐渐增大,边缘的皮质骨孔隙率较低,主要起力学承载作用,中心的松质骨孔隙率则较高,能够进行物质传递[4]。梯度多孔支架克服了均质多孔支架结构性能单一的问题,能够较好地满足力学性能与生物相容性要求。此外,股骨和胫骨的受力情况复杂,最具代表性的受载工况是双足静止站立时的受载情况,对于骨骼长期受载,需要具备良好的能量吸收特性,避免意外过载或局部应变造成骨组织的损坏。因此,多孔骨支架除了需要具备适合的力学性能和生物相容性外,同样需要具备较好的能量吸收特性,使其手术后具有长期稳定性。
选区激光熔化(selective laser melting,SLM)技术是一种近年来获得广泛关注与快速发展的增材制造技术,具有成形精度高、组织致密等技术优势,在金属零件加工制造领域具有广泛的应用前景[5]。三周期极小曲面(triply periodic minimal surface,TPMS)具有在指定边界内面积最小、所有点的平均曲率为零以及在三个独立方向上具有无限周期的特点[6],可以通过数学表达式生成具有光滑表面的TPMS多孔结构,从而减少应力集中,也可以根据特定要求调整结构尺寸、孔隙率的梯度分布[7]。因此,TPMS被认为是最有前途的生物多孔结构[8]。LEI等[9]发现孔隙率连续变化的TPMS梯度多孔支架在力学性能、能量吸收能力方面均高于均质多孔结构;XIONG等[10]设计的用于承载骨的分层梯度多孔支架具有良好的力学性能和能量吸收能力。
尽管目前关于梯度多孔支架的设计制备和力学性能等方面的研究工作取得了一定的进展,但是梯度多孔支架结构设计参数与力学性能、能量吸收能力之间的影响规律还有待进一步研究。为此,本文基于TPMS中的常用Diamond结构,设计不同孔隙率分布的梯度多孔支架,并应用选区激光熔化技术制备出Ti6Al4V支架样件,通过压缩试验模拟受载工况,研究梯度多孔结构的力学性能和能量吸收性能,揭示相关结构参数对梯度多孔结构力学性能和能量吸收性能的影响规律,为面向骨科医学多孔支架的应用提供设计依据。
1 设计和实验方法
1.1 梯度多孔支架设计
Diamond曲面结构的数学表达式为
(1)
式中,x、y、z为空间上三个方向的坐标;l为曲面周期;C为偏置量[11]。
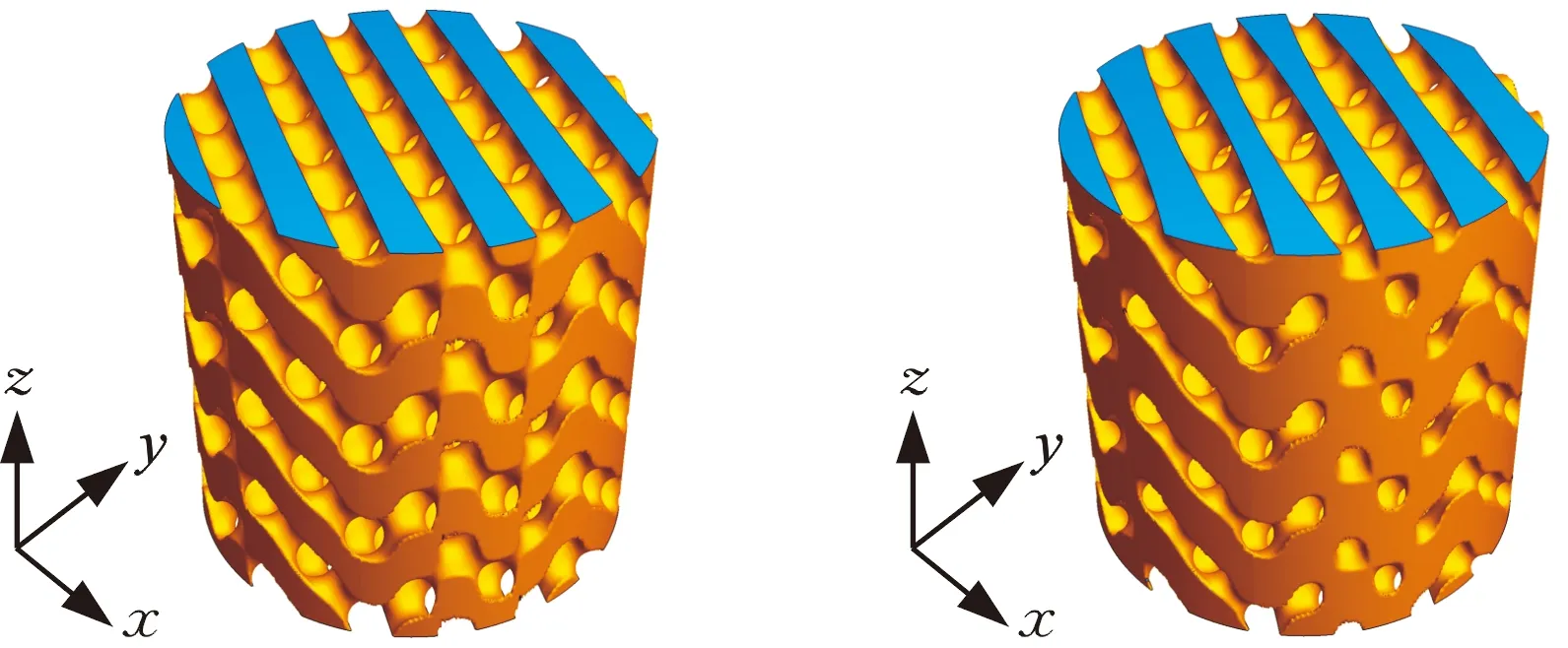
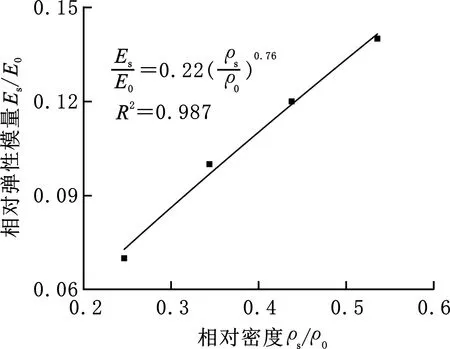
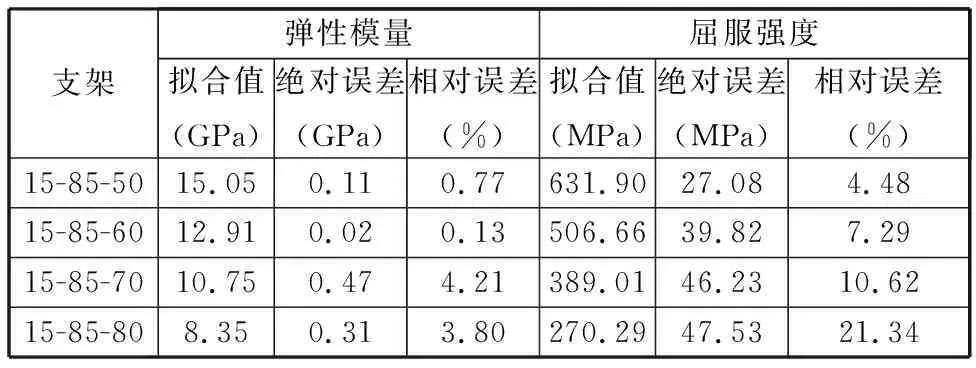
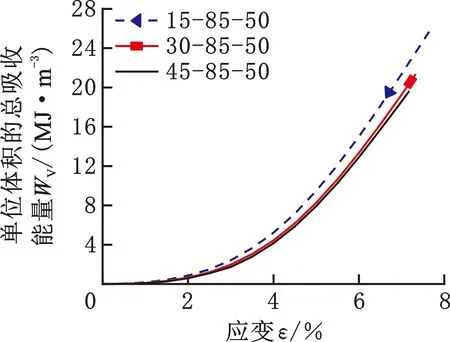
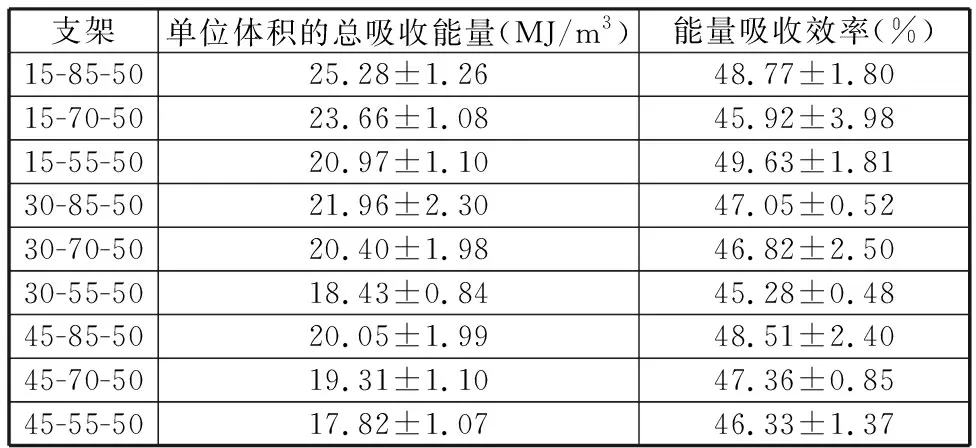
式(1)所代表的曲面是实体区域与孔隙区域的交界面,U(x,y,z)>C为实体部分,U(x,y,z) 图1 偏置量C与孔隙率PU之间关系Fig.1 Relationship between C and porosity PU 通过图1可以得出,Diamond多孔结构的C与孔隙率PU关系为 PU=(0.4146C+0.5)×100% (2) 为了实现孔隙率的连续梯度分布,采用偏置量设计方法: (3) 其中,k、b、n三个参数控制着孔隙率的梯度分布[12]。若梯度多孔支架高为H,结构半径为R,则结构中心的自变量半径r=0、边缘的自变量半径r=R处的孔隙率分别为中心孔隙率Pin、边缘孔隙率Pout;Pin、Pout对应的偏置量分别为Cin、Cout。在给定n的前提下,将Cin、Cout分别代入式(3),可以求得k、b: (4) b=Cin (5) 将式(2)、式(4)和式(5)代入式(3)得 (6) 将式(6)代入式(2)则得到该梯度多孔支架的孔隙率分布函数: (7) 梯度多孔支架的平均孔隙率为 (8) 式中,V为梯度多孔支架孔隙部分体积。 U(x,y,z)>-0.0345(x2+y2)+0.8442 (a)45-55-50 (b)30-70-50 实验采用Ti6Al4V金属粉末,其各元素含量见表1所示,利用TM3030Plus扫描电子显微镜(SEM)对粉末进行观测,粉末形貌如图3所示,呈现规则球形,具有良好的流动性。使用SLM设备(SLM125)打印梯度多孔支架,一共打印三组样件。成形工艺参数为:激光功率275 W,扫描间距0.12 μm,扫描速度为1100 mm/s,铺粉厚度30 μm。成形过程采用氩气(浓度为99.99%)保护,成形舱的氧气含量小于0.1%。打印的一组样件如图4所示。 表1 Ti6Al4V粉末的化学成分(质量分数) 图3 Ti6Al4V粉末的微观形貌Fig.3 Micro-morphology of Ti6Al4V powder 图4 SLM打印的一组样件Fig.4 A set of samples printed by SLM 在进行形态和机械表征之前,先采用超声波清洗法将样品浸入乙醇溶液(95%)中,以洗净残留粉末。使用数字显微镜观测宏观形貌,使用SEM观测微观形貌。采用称重法测量梯度多孔支架的孔隙率[4](即平均孔隙率),其公式为 式中,m1为与支架相同外形尺寸实心支架质量;m2为测得的多孔支架质量。 使用电子万能试验机(DNS300)进行轴向压缩试验,压缩速度为2 mm/min。 所观测的梯度多孔支架的宏观形貌如图5所示,可知支架内部连通、孔隙率具有由内向外的梯度分布。这种孔洞相互连通、孔隙率梯度分布的支架,已被证明有助于骨生长、能够减少植入物的应力屏蔽和保持机械强度[10,14]。梯度多孔支架的微观形貌如图6所示,支架表面存在未熔化的粉末和挂渣,这是SLM技术成形造成的,未熔和熔融粉末之间发生热扩散,导致粉末黏附在支架表面[15]。 (a)45-55-50 (b)30-70-50 图6 梯度多孔支架的微观形貌Fig.6 Micro-morphology of gradient porous scaffolds 三组梯度多孔支架样件测得的实际平均孔隙率和标准差如表2所示,由实验结果可以看出,测得的支架样件的实际孔隙率均小于设计孔隙率。究其原因,主要是由于采用SLM技术打印梯度多孔支架时,支架表面不可避免地会存在粘粉和挂渣现象,使得测量获得的样件质量比设计模型质量偏大,导致计算获得的孔隙率小于设计值。这一实验结果与SLM技术原理有关,无法通过优化工艺参数来完全消除,通过文献对比,这一现象与文献[11,16-17]的研究结果相同。 表2 梯度多孔支架的孔隙率 对实验方案1打印获得的9种梯度多孔支架进行静态轴向压缩试验,应力-应变曲线如图7所示。通过分析其变化规律可以看出:曲线前端初始阶段所有支架样件的应力-应变曲线都存在非线性区域,这是因为压缩开始时样件端面与压头平面未完全贴合[10];接着曲线呈现一个近似直线的弹性变形阶段;最后,当应力达到峰值时,发生与文献[11]相似的坍塌现象。 (a)Pin=85% 由于不同年龄、不同体质以及不同骨骼的弹性模量和抗压强度不完全一样,制备所得的多孔骨支架的弹性模量应该匹配对应骨骼部位的弹性模量,抗压强度则需大于人骨的最大强度值,以减轻“应力屏蔽”效应。实验测得的9种支架的力学性能如表3所示,弹性模量范围在(12.35±0.14)~(14.94±0.16) GPa之间,而抗压强度范围在(565.88±24.56)~(685.22±11.57) MPa之间。文献[18]的研究表明,人体股骨的弹性模量为11.2~18.9 GPa,抗压强度为155~215 MPa,故实验方案1制备的9种梯度多孔支架的弹性模量、抗压强度满足股骨的要求。 表3 9种梯度多孔支架的力学性能 通过表3所示的实验数据制作Pout、Pin与力学性能关系图,见图8。可以看出:当Pin相同时,弹性模量与抗压强度都随着Pout的增大而减小;当Pout相同时,弹性模量与抗压强度都随着Pin的增大而增大。 (a)弹性模量 图9 4种梯度多孔支架的应力-应变曲线Fig.9 Stress-strain curves of four gradient porous scaffolds 表4 4种梯度多孔支架力学性能 Gibson-Ashby公式是描述多孔结构密度和力学性能之间关系的重要数学模型,该公式可为多孔支架力学性能的评估、预测及设计制造提供理论支撑,表达式如下: (11) (12) 式中,Es、ρs、σs分别为多孔支架的弹性模量、密度、屈服强度;E0、ρ0、σ0分别为完全致密体材料的弹性模量、密度、屈服强度;Es/E0是相对弹性模量;σs/σ0为相对屈服强度;ρs/ρ0为相对密度(体积分数)。 而Ti6Al4V完全致密体材料的弹性模量是110 GPa,屈服强度是869 MPa[12]。 Gibson-Ashby公式的拟合结果如图10所示,相对弹性模量、相对屈服强度与相对密度成幂函数关系,两者都有较好的拟合度R2,R2分别达到0.987、0.922。弹性模量和屈服强度的拟合值及分析结果如表5所示,弹性模量的相对误差均小于屈服强度的相对误差。弹性模量最大的绝对误差和相对误差分别为0.42 GPa、4.21%。屈服强度的绝对误差和相对误差都随着孔隙率的增大而增大,虽然绝对误差和相对误差的最大值分别为47.53 MPa、21.34%,但是屈服强度拟合值和实验值都大于股骨、胫骨的抗压强度,故该拟合结果可以为面向医学骨科多孔支架的应用提供参考。 (a)相对弹性模量 表5 拟合值及分析结果 梯度多孔结构因在能量吸收方面的潜力而备受关注。单位体积的总吸收能量WV如下[7]: (13) 能量吸收除了WV外还可以用能量吸收效率η指标来表示: (14) 式中,σmax为最大应力。 (a)Pin=85% 图12 9种度多孔支架的WV与Pin、Pout关系Fig.12 Relationship between WV of nine gradientporous scaffolds and Pin,Pout 表6 九种梯度多孔支架的能量吸收 图13 四种梯度多孔支架的WV与ε关系Fig.13 Relationship between WV of four gradient porous scaffolds and ε 表7 4种梯度多孔支架的能量吸收 (1)采用选区激光熔化技术打印成形的Ti6Al4V梯度多孔支架成形效果良好,与基于TPMS中Diamond结构设计的模型匹配度高。同时支架内部连通,具有由内向外孔隙率梯度变化的特性,可以较好地模拟人体股骨、胫骨等天然骨的梯度多孔特征。 (2)梯度多孔支架结构参数会影响其力学性能和能量吸收性能。平均孔隙率和边缘孔隙率越小、中心孔隙率越大,梯度多孔支架的弹性模量、抗压强度和单位体积总吸收能量就越大;平均孔隙率对弹性模量、抗压强度和单位体积总吸收能量的影响大于边缘孔隙率和中心孔隙率的影响;多孔支架各结构参数对能量吸收效率指标的影响较小。 (3)利用Gibson-Ashby理论公式建立的梯度多孔支架力学性能模型有较好的拟合度和较小的相对误差,实验制备所得的支架样件能够满足股骨和胫骨的弹性模量、屈服强度等力学性能要求。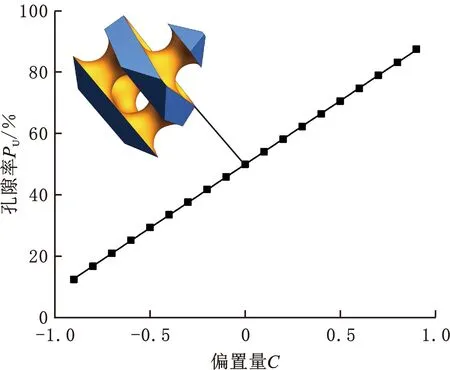
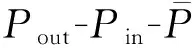
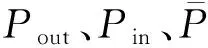
1.2 实验材料与工艺参数



1.3 测试方法
2 实验结果与分析
2.1 梯度多孔支架表面形态



2.2 力学性能研究







2.3 能量吸收研究

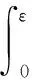

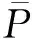

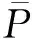


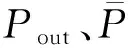
3 结论
