东部地区全要素生产率测算与分析

□文/朱夏婷

（福州大学经济与管理学院 福建·福州）

［提要］ 基于2000～2019 年东部11 个省（市）面板数据，运用随机前沿分析模型对东部地区全要素生产率增长进行测算和分析，并采用固定效应面板回归模型对全要素生产率进行影响因素研究。研究结果表明：技术进步是东部地区全要素生产率增长的主要动力，且东部各个经济圈之间的全要素生产率具有空间差异性。提高基础设施水平和市场化水平有利于促进东部地区全要素生产率增长，城镇化水平和科研投入的提高会对全要素生产率起阻碍作用。

改革开放以来，中国经济凭借“要素投入”和“人口红利”实现了持续高速发展，但随着人口老龄化，自然资源短缺和劳动力成本上涨等问题的出现，依靠要素投入的粗放式经济增长模式已不可持续。中国经济转变增长方式刻不容缓。十九大报告指出，必须坚持质量第一、效率优先，以供给侧结构改革为主线，推动经济发展质量、效率和动力变革，提高全要素生产率（TFP）。

1957 年美国经济学家罗伯特·索洛第一次将技术进步引入经济增长模型，将人均产出增长扣除资本集约程度增长后的部分归因于技术进步，并称其为技术进步率，也就是全要素生产率的增长率。自索洛开拓性研究以来，对全要素生产率的研究层出不穷，成为国家、地区、行业等经济单位经济运行质量的定量评估指标。20 世纪80 年代，中国引入全要素生产率的概念和测算方法，开始结合实际研究全要素生产率增长率。

在当前开放性经济大背景下，东部沿海地区凭借优越的地理位置成为我国改革开放的试点，区域经济获得优先快速发展。对东部地区各省市全要素生产率进行测算，研究影响因素，对推动区域经济高质量发展和实现国家战略目标有重要的现实意义。

一、东部地区全要素生产率测算与分析

（一）模型方法。本文采用Battese & Coelli（1992）版的随机前沿分析模型（SFA）对东部地区全要素生产率进行测算。SFA方法具有以下几个优点：（1）属于统计方法，具备统计特征，可以对模型本身进行检验；（2）既考虑了技术非效率的影响，又考虑到了随机因素的影响；（3）既可以直接计算出每个生产单元的技术效率，又可以就个体之间技术效率的差异进行深入分析。随机前沿模型描述如下：

其中，i 表示决策单元，在本文中代表东部各个省（市），t 表示时间趋势项，Yit代表地区i 在时期t 的实际产出，f（·）为前沿生产函数，表示当前要素投入比例下，能够产出的最高水平。Xit表示i 省（市）在时期t 的一组要素投入，α 为待估计的参数向量，νit-uit为复合误差项，其中νit为随机误差，服从正态分布，uit为生产无效率项，服从截断正态分布。将公式（1）两边取对数，可以得出以下对数随机前沿模型：

本文采用C-D 生产函数的随机前沿模型进行全要素生产率的测算，式（2）转化为：

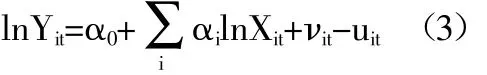
（二）研究变量与数据来源。从投入和产出两个维度讨论变量：

1、选取各个省（市）历年的实际地区生产总值作为产出变量。将历年的名义GDP 通过GDP 指数折算成以2000 年为基期的实际GDP。

2、选取各省（市）历年的物质资本存量和劳动力投入作为投入变量。其中，物质资本存量参考张军（2004）的做法，将固定资本形成额作为当年投资并利用固定资本投资价格指数折算成实际投资，把9.6%作为折旧率，采用永续盘存法计算出历年的固定资本存量。另外，劳动力投入用各省（市）历年年末就业人员数来表示。

本文的研究样本为东部地区的11 个省（市），包括北京、天津、河北、辽宁、上海、江苏、浙江、福建、山东、广东和海南，时间跨度为2000～2019 年。数据主要来源于《中国统计年鉴》和各省（市）的地方统计年鉴。

（三）东部地区全要素生产率增长具体测算。通过对东部地区 11 个省（市）2000～2019 年投入产出数据，利用 stata 软件估计回归系数，参数估计结果见表1。（表1）

表1 SFA 模型的参数估计结果一览表

将全要素生产率增长率分解为技术效率和技术进步，并结合公式计算出历年东部地区TFP 增长率，结果见表2。从表2中可以看出，技术进步指数在2000～2019 年期间一直大于1，对于全要素生产率具有促进作用，而技术效率指数在这一期间一直小于1，说明对于全要素生产率的增长具有削弱的作用。（表 2）

表2 2000～2019 年东部地区全要素生产率年增长指数分解一览表

为分析全要素生产率在空间区域上的差异，本文将东部11 省（市）分成环渤海经济圈、长三角经济圈和泛珠三角经济圈。环渤海经济圈包括北京、天津、河北、辽宁、山东；长三角经济圈包括上海、江苏、浙江；泛珠三角经济圈包括福建、广东、海南。将2000～2019 年平均分成10 个时间段，2 年为一组计算每个经济圈的全要素生产率年平均指数，结果如表3 所示。为了更加直观地对比三个经济圈的全要素生产率指数情况，本文用表3 的数据绘制了折线图，如图1 所示。从图1 可以看出，长三角经济圈在三个经济圈中处于上峰，其次是泛珠三角经济圈，最后是环渤海经济圈。另外，从图1 可以看出，长三角经济圈全要素生产率呈上升发展趋势，泛珠三角和环渤海经济圈自2006/2007 年后呈下降趋势，其中环渤海经济圈在2018/2019年开始逆转趋势，出现上升势头。（表3、图1）

图1 2000～2019 年各经济圈平均全要素生产率指数走势图

表3 2000～2019 年按经济圈全要素生产率平均年增长指数一览表

二、东部地区全要素生产率影响因素分析

（一）模型设定。本文采用面板回归对全要素生产率的影响因素进行分析研究，模型设定如下：

其中，i 表示决策单位，这里表示各个省（市），t 表示时间趋势项，tfpit代表地区i 在t 时期全要素生产率增长率，β0是截距项，βi是各个解释变量的回归系数，X 代表解释变量，Xit表示i省（市）在时间t 的一组解释变量值，μit代表随机误差。

（二）变量说明和数据来源。根据已有的研究，选择以下6个变量作为全要素生产率增长率的解释变量：（1）开放程度（进出口贸易总额占GDP 比重）；（2）基础设施水平（每平方面积公路里程数）；（3）人力资本（每万人高等教育在校人数）；（4）城镇化水平（城镇人口占比）；（5）市场化水平（参考樊纲（2011））；（6）科研投入（R&D 内部经费支出），如表4 所示。在计算时，对上述6 个变量都取对数，解释变量就是全要素生产率增长率tfp。以上变量的原始数据来自于《中国统计年鉴》《中国科技统计年鉴》和各省（市）地方统计年鉴的2000～2019 年的11 个省份年度数据，其中市场化水平指标取值来源于中国市场化指数数据库。（表4）

表4 解释变量说明一览表

（三）数据处理。在正式进行模型计算之前，对数据进行平稳性、协整性检验。首先，本文对7 个变量数据进行平稳性分析，检验结果为：开放程度通过了时间趋势检验，其他变量都通过滞后两期的平稳性检验。其次，对变量做协整性检验，ADF 检验的P 值为0.0520，说明在显著度10%的程度上，变量具有协整性。

固定效应、随机效应选择。首先，对变量数据进行F 检验，得到p 值为0，表示拒绝混合回归，选择固定效应。其次，对变量数据进行Hausman 检验，结果显示p 值为0.0130，在5%的显著度上拒绝随机效应，应当选择固定效应。因此，本文选择带固定效应的面板回归模型。

（四）模型回归结果及分析。本文采用stata 软件利用固定效应模型对变量数据进行回归分析，回归结果见表5。（表5）

表5 固定效应面板回归结果一览表

1、开放程度。从表5 中可以看出，开放程度提高对全要素生产率增长存在负作用，开放程度每提高一个百分点，全要素生产率增长将会下降0.0128 个百分点，但是开放度系数并未通过10%显著度的检验，说明开放程度对全要素生产率的影响并不明显。开放程度这一指标系数为负，可能是因为虽然贸易的总量在扩张，但是贸易的结构并不合理，导致产业结构的不合理，要素扭曲配置。

2、基础设施水平。基础设施水平的指标系数为0.0827，意味着基础设施水平每提高一个百分点，东部地区的全要素生产率增长提高0.0827，说明基础设施水平对全要素生产率起正向促进作用，且系数通过了1%显著度的检验。完善的基础设施可以降低运输成本，有利于生产要素的流动，有助于一体化市场的形成，从而促进区域经济的发展。

3、人力资本。人力资本指标的系数为正，意味着人力资本水平每提高1 个百分点，全要素生产率增长提高0.0148 个百分点，人力资本对全要素生产率具有正向促进作用。但是，人力资本指标的系数并未通过10%显著度的检验，说明人力资本对全要素生产率的影响并不明显。人力资本的正向作用可以通过推动科技创新从而提高全要素生产率增长。

4、城镇化水平。城镇化水平指标系数为负，意味着每提高一个百分点城镇化水平，就会使全要素生产率增长下降0.248个百分点，并且其系数通过了1%显著度的检验。城镇化对全要素生产率产生负作用，可能是由于东部地区城镇化的推进速度过快，造成了技能水平较低的劳动力的过度供给，与当地的产业不匹配，政府为了解决就业问题，被迫选择能提供更多就业岗位的企业，对产业结构优化产生负作用，造成全要素生产率增长下降。

5、市场化水平。市场化水平的指标系数为正，意味着市场化水平每提高一个百分点，全要素生产率增长提高0.253 个百分点，且其系数通过了1%显著度的检验。市场化水平越高，说明市场对资源的配置作用更强，有效解决要素配置扭曲的问题，促进生产要素流向效益高的行业企业，有利于技术效率的提高，从而提高全要素生产率增长。

6、科研投入。从表5 可以看出，科研投入指标系数为负，意味着科研投入水平每提高一个百分点，全要素生产率增长下降0.203 个百分比，且其系数通过了1%显著度的检验。科研投入对全要素生产率增长具有负作用，可能是跟R&D 经费的投资结构有关，即公共研究机构和企业科研经费的比例。公共研究机构的R&D 投入可能会对企业的全要素生产率产生负影响。在一定时间内，可用于科技研究的经费是有限的，用于公共研究机构多了，则能够提供给企业的，特别是中小企业的经费就会减少。并且，R&D 经费投入的研究方向如果过多地集中在风险高且资金密集的技术项目上，对企业的技术效率可能会造成负面影响。

三、结论及建议

（一）结论。（1）2000～2019 年全要素生产率呈先上升再下降的趋势，其中技术效率对全要素生产率增长起阻碍作用，技术进步对全要素生产率增长起促进作用；（2）东部地区各经济圈空间差异明显，长三角全要素生产率增长率高于环渤海和泛珠三角经济圈，且呈良好的发展态势，环渤海和泛珠三角经济圈近几年全要素生产率增长呈下降趋势；（3）面板回归结果显示，基础设施、市场化水平对全要素生产率增长起促进作用，城镇化、科研投入对全要素生产率增长起阻碍作用，开放水平、人力资本并未通过显著度检验，作用效果不明显。

（二）建议。（1）科技效率一直阻碍全要素生产率增长，说明生产要素的配置存在扭曲，政府需要通过协调各种要素的配比来提高技术效率，充分释放技术水平潜能，比如大力发展中介机构，促进市场各参与者之间的信息交流和沟通；（2）为促进区域全要素生产率均衡发展，环渤海、泛珠三角经济圈可以借鉴长三角的发展经验，推广复制，取长补短；（3）为推进东部地区整体全要素生产率的提高，政府要加大基础设施投入，完善交通设施，加快市场化改革进程，促进要素的自由流动；（4）政府应当科学地推进城市化进程，如果某些城市城镇化率过高，接踵而至的城市病可能会阻碍全要素生产率的发展，不合理的劳动资本配合也会阻碍产业结构升级，从而遏制全要素生产率增长；（5）政府应当合理规划R&D 经费投入，科学合理地选择分配的对象和研究领域，实现1+1＞2。