空化泡-边界相互作用研究进展综述

2022-10-18张宇宁孙卓

核科学与工程 2022年3期

张宇宁，孙卓

（1.华北电力大学电站能量传递转化与系统教育部重点实验室，北京 102206；2.华北电力大学能源动力与机械工程学院，北京 102206）

空化泡动力学是核工程领域中一项十分值得关注的重要课题。在核电站设备及其附属的泵[1]、管道[2]，以及相关的阀门[3]、孔板[4]等过流部件中，液体的高速流动和局部压力骤降，经常会导致空化现象的产生，在部件材料附近不断形成微小的空化泡并溃灭。大量、长期的空化泡溃灭会对材料表面产生严重破坏，同时伴随着强烈的噪音和异常振动，极大地增加了核电站的安全隐患和维护成本[5]。所以，对空化泡射流及其对边界材料的冲击作用的研究具有重大的工程意义[6,7]。

相关研究表明，空化泡在固体材料附近溃灭时，会在材料表面附近产生瞬时局部高压和高速微射流。在此过程中，高速射流已被证明是导致材料损伤的最显著机理[8]。因此，为了系统地阐释空化泡与边界相互作用的微观机理，本文从理论研究方面入手，结合射流实验研究，对边界附近的单个球形空化泡的溃灭射流相关研究进行综述。

理论研究方面，空化泡的射流强度和方向可以用Kelvin 冲量来预测。Kelvin 冲量是非定常流体力学中一个特别有价值的动力学概念，是根据势流理论推导出的表征空化泡运动状态的一个量，其实质相当于空化泡在整个周期内的动量变化量[9]。下面，本文将简要回顾空化泡 -边界相互作用的Kelvin 冲量理论和空化泡射流方面的相关研究。

Benjamin 和 Ellis[10]早在 1966 年首次将Kelvin 冲量应用于空化泡动力学，以解释边界附近空化泡的非球形变形、射流的形成以及空化泡的运动。其后，Blake等[11-14]在空化泡Kelvin 冲量方向做了大量工作，进一步奠定了该方法的理论基础，推导了多种边界情况下空化泡Kelvin 冲量的近似解析表达式，并通过实验与数值研究证实了空化泡Kelvin 冲量与溃灭射流间的联系，使空化泡 -壁面相互作用的研究向前推进了一大步。Best 和Blake[15]在已有Kelvin 冲量理论的基础之上，基于Lagally 定理将空化泡所受Bjerknes 力表达式进行简化，进而简化了空化泡Kelvin 冲量计算公式。实验研究方面，Lauterborn 和Bolle[16]在1975 年利用高速摄影技术对刚性水平壁面附近的激光诱导空化泡进行了细致的实验研究，通过250 000帧/秒的高速摄影图像测量到了壁面附近空化泡射流尖端速度高达120 m/s。Vogel等[17]通过高速摄影实验进一步研究了水平壁面附近空化泡射流行为与空化泡 -壁面间无量纲距离的关系，并深入讨论了射流造成的空蚀机理。

近年来，许多学者对空化泡 -边界相互作用研究进行丰富和拓展，探究了不同边界附近空化泡的泡动力学行为以及射流情况。Tagawa和Peters[18]对不同角度的角形壁面附近空化泡射流进行了实验研究，分析了射流角度随空化泡位置角度的变化规律，并且计算验证了Kelvin 冲量角度与射流角度的对应关系。Bempedelis等[19]对空化泡与自由液面的相互作用进行了实验研究，围绕射流高度、宽度、尖端速度以及射流在时间尺度上的演化等展开讨论，并结合数值研究，分析了空化泡诱导雾化的机理。Brujan等[20]研究了直角壁面附近激光诱导空化泡的行为，对空化泡与水平壁面和垂直壁面间不同距离情况下的射流等行为进行了细致的实验研究。Zhang等[21]利用高速相机对球形颗粒附近的激光诱导空化泡进行实验研究，对溃灭形状、射流行为进行了详细的分析。Zhang等[22,23]还研究了球形颗粒与固体壁面的复合边界对空化泡溃灭和射流行为的影响。

总体而言，空化泡 -边界相互作用是泡动力学领域中的一个重要方向，多年来吸引了众多国内外学者开展研究。然而，尽管Best 和Blake[15]在20 世纪 90 年代就已提出空化泡Kelvin 冲量理论可用于边界附近空化泡射流行为的预测及理论解释，但遗憾的是，目前在空化泡 -边界相互作用研究中，大多缺乏深入的理论与实验结合，Kelvin 冲量理论的应用非常有限。

因此本文系统地回顾推导Best 和Blake 的Kelvin 冲量理论，简要梳理具体计算流程并指出核心问题的解决思路。同时，综述了相关边界条件下的射流实验研究结果以展示Kelvin 冲量理论的可靠性。此外，对Kelvin 冲量理论与高速摄影实验研究可能的结合点提出了建议，并给出了适用条件。本文的章节安排如下：第1 节系统地展示并优化了Kelvin 冲量理论的推导过程，并总结出了其通用计算流程。第2 节介绍了用以处理边界对空化泡影响的镜像法原理及应用。第3～6 节分别对水平壁面、自由液面、角形壁面以及球形颗粒四种边界附近Kelvin 冲量的计算与分析进行展开，并展示了相应边界附近空化泡射流的实验研究结果。第7 节对上述工作进行了总结，并对Kelvin 冲量理论与高速摄影实验研究可能的结合点进行了细致讨论。

1 Kelvin 冲量理论

Blake等[11,14]从流体动量的基本概念出发，提出了不可压缩流体中空化泡Kelvin 冲量的理论公式。在此基础上Best 和Blake[15]将边界作用于空化泡的Bjerknes 力与泡内速度势奇点的强度联系起来，进而得出一种简化的通用计算公式，可更简捷地计算空化泡Kelvin 冲量。本节将系统地回顾空化泡Kelvin 冲量理论，对其中 Blake 等未展示的中间过程进行细致推导，最后对Kelvin 冲量计算流程进行较清晰的梳理。

1.1 Kelvin 冲量理论推导式

假定体积为V′、边界面为S′的无粘势流控制体初始动量为零，其冲量即为动量变化量[11]

式中：I——控制体所受冲量；

ρ——流体密度；

dV——流体的体积微元；

u——流体局部速度；

Φ——流体局部速度势；

n——流体外法线单位向量；

dA——流体的面积微元。

在针对半无限流体中边界附近空化泡的Kelvin 冲量理论中，如图1 所示选取体积为V′的控制体，其边界S′由三部分构成：空化泡表面S、半无限流体的平面边界的控制表面Σb、外部边界面Σ。根据式（1），控制体的冲量可表示为两积分之和[11]

图1 选取的控制体及其边界示意图[11]Fig.1 The schematic of selected control body and its boundaryx=0[11]

式中：IS——空化泡表面S所受冲量；

——控制体其他边界面Σ∪Σb所受冲量。

对于有限体积V中流体动量的变化率，等于作用在控制体上的合力F，即[11]

式中：t——时间；

p——某点处的流体压强。

假设泡内蒸汽均匀分布，则空化泡表面S上的压力是均匀的，并近似等于空化泡内的饱和蒸气压，因此式（3）右侧括号内的第一个积分为零[11]。

将式（2）带入式（3），变形可得

连续介质中的雷诺传输定理如下[24,25]

式中：f——可以是张量、标量或向量函数。

根据雷诺传输定理，对式（4）等式右侧第二项进行化简

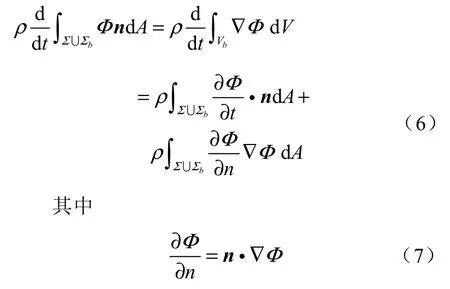
式中：Vb——边界面Σ∪Σb所对应的体积。

根据非定常伯努利方程，在不考虑重力势能时有

式中：p∞——无穷远处的流体压强。

将式（6）、（8）带入式（4）中整理可得

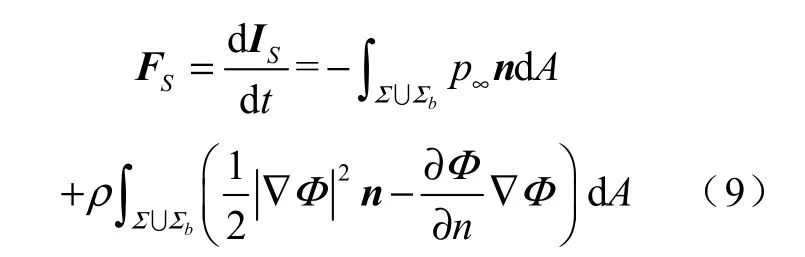
式中：FS——空化泡所受合外力。

当选取的控制体体积足够小时，可近似认为面S与面Σ∪Σb表面重合、法向方向相反，因此可通过以下等式将空化泡所受合外力表示为面S上的积分[11]

将式（10）代入式（9）可得[11]

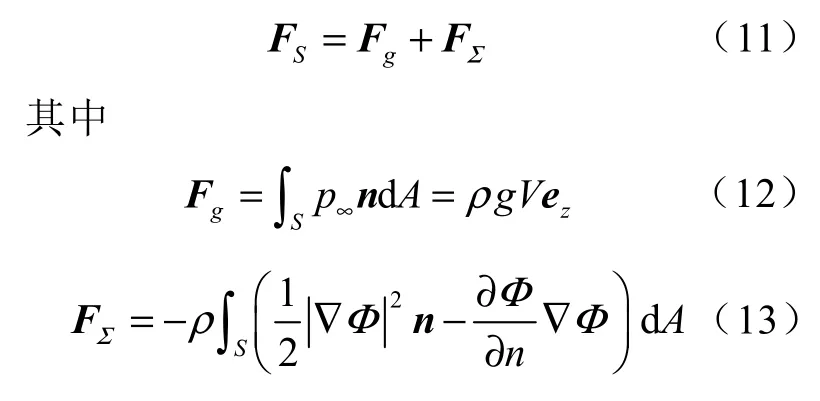
式中：Fg——空化泡所受浮力；

FΣ——空化泡所受Bjerknes 力；

ez——竖直方向的方向向量。

根据冲量与所受作用力之间的关系，空化泡所受Kelvin 冲量计算公式即[11,15]

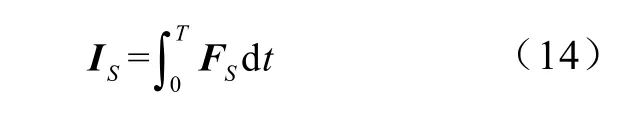
式中：T——空化泡周期。

1.2 空化泡Bjerknes 力简化

Landweber 和Miloh 基于Lagally 定理建有以下方程[26]

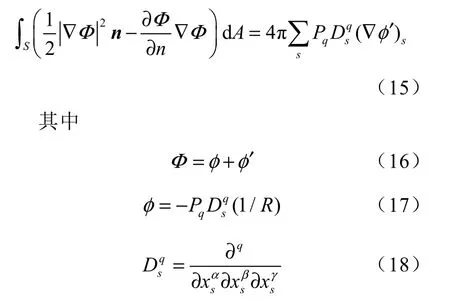
式中：Φ——边界存在时空化泡附近流体的速度势；

φ——无限大流场中空化泡附近流体的速度势；

φ′——边界作用产生的空化泡附近流体的附加速度势；

q——求和约定数，满足α+β+γ=q；

()s——对速度势奇点s处的求值；

R——空化泡瞬时半径。

将式（15）代入式（13），可得由奇点速度势表示的Bjerknes力[15]

本文假设流体为无粘、不可压缩的均匀理想流体，空化泡表面与内部的压力和温度均匀恒定，空化泡表面不存在热量传递和质量传输，且空化泡的非球形扰动足够小。可用点源模型表示空化泡流场的速度势：

式中：m——源强，即单位时间从点源释放的流体体积；

——空化泡瞬时半径对时间的一阶导数，即空化泡壁面处的径向速度。

对空化泡流场而言，唯一的速度势奇点为点源中心r0，根据式（17）与式（20）可知，此时求和约定数q=0，代入式（19），Bjerknes力可进一步简化为[15]

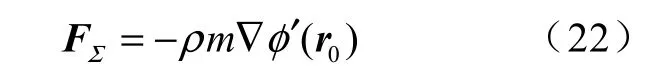
其中，边界干扰产生的附加速度势φ′可写为以下形式[15]

其中g(r)的具体形式取决于边界情况，可通过镜像法求得，本文第二节将详细介绍镜像法的概念、原理及具体应用案例。

将式（22）、（23）联立，再引入参数Γ，可将Bjerknes 力进一步简化表示为[15]

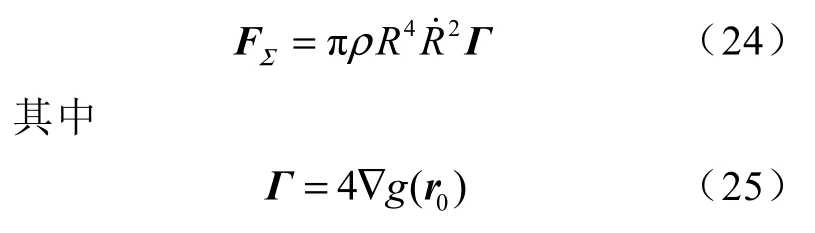
1.3 Kelvin 冲量简化计算式

要对简化的Bjerknes 力积分得出Kelvin 冲量，须求出空化泡泡壁瞬时速度R˙。为方便快速计算，本节推导过程中的变量将分别以下列规定的对应尺度进行无量纲化：以空化泡最大半径Rmax作为长度尺度，以远场压力与泡壁处液体压力之差Δp=p∞-pR作为压力尺度，以作为时间尺度[15]。本节以“*”表示参数的无量纲形式。

对非定常伯努利方程进行无量纲化可得[15]

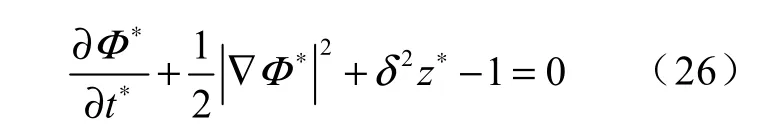
式中：δ——无量纲浮力参数，满足

将式（16）、（20）、（21）代入式（26）可得[15]

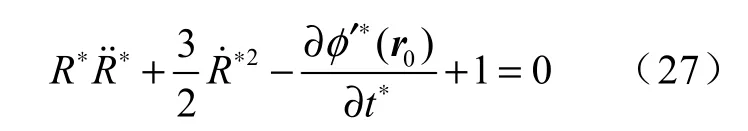
式中：r0(x0,y0,z0)——空化泡中心的坐标向量。

将式（23）带入（27）可得[15]

已知当空化泡尺寸达到最大值时R*=1、= 0，于是对式（30）求解可得[15]

将浮力无量纲化，整理可得[15]

将无量纲浮力、Bjerknes 力代入式（14），即可计算空化泡所受Kelvin 冲量[15]

将式（31）代入式（33）、式（34），整理可得无量纲Kelvin 冲量简化计算式[15]

式中：B(a,b) ——贝塔函数[27]。

综上，本节详细推导了边界附近空化泡无量纲Kelvin 冲量通用计算公式。具体而言，计算流程如下：

（1）根据流场边界的具体性质和几何条件，利用镜像法得出边界作用的附加速度势φ′；

（2）对于边界附加速度势φ′，代入式（23）、式（25）和式（29），得到参数Γ*和μ；

（3）将上述参数代入通用计算公式（35）和公式（36），即可求得空化泡所受无量纲Kelvin 冲量。

2 镜像法原理及应用

根据第1 节可知，在空化泡Kelvin 冲量简化计算方法中，关键步骤为通过镜像法求得边界作用的附加速度势φ′。因此本节介绍镜像法的原理，并讨论其具体应用。

2.1 镜像法原理

镜像法的概念起源于静电学问题，其基本理论依据是等效原理和唯一性定理[28]。镜像法也被应用于流体力学领域，通过在流场边界外添加镜像项来等效边界对流场的影响。对于无粘、不可压缩势流中的刚性壁面，添加镜像项后应满足不可穿透壁面条件，即流体在刚性壁面上的法向分速度为零，而在沿着壁面的切向分速度不一定为零[29]。

2.2 水平壁面镜像法应用

为计算与表达的方便起见，本节在二维平面上进行镜像法应用案例的推导与讨论，以复平面取代x-y平面，用复数表示平面上的坐标。

任意平面势流的速度势函数φ和流函数ψ都满足柯西 -黎曼条件，因此以φ为实部和以ψ为虚部可以构造一个解析函数，称为复位势[29]

以实轴为边界的镜像法平面定理如下：假设奇点只在y＞ 0区域内，无壁面存在时其复位势为f(z)，如果流场中存在与实轴相重合的水平壁面，则奇点在上半平面产生的复位势为[29]

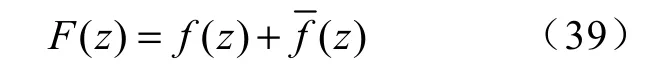
根据式（40）可知，实轴上F(z)只有实部φ而虚部ψ为零，即实轴上法向分速度为零。同时，的奇点只在y＜ 0的区域内，未在上半平面增加新的奇点，因此上半平面F(z)的奇点和f(z)的奇点完全相同，F(z)是除原奇点外的解析函数，证明式（39）是满足实轴为边界的复位势[29]。

以水平壁面上方z=z0处的沿逆时针方向的点涡为例，其本身的复位势为[29]

将上式代入式（39）中，可得[29]

上式即所求水平壁面上方的复位势。如图2所示，相当于除了原来位于z0点的点涡外，又在z0点关于实轴的对称点=x-iy处添加了一个强度相同、旋转方向相反的点涡，以满足镜像法的等效条件[29]。

图2 水平壁面上方的点涡及其镜像[29]Fig.2 The point vortex and its mirror image above the horizontal wall[29]

以上内容以水平壁面为例，展示了利用镜像法求边界附加速度势的推导过程。总体而言，对于任何种类的刚性边界，只要能满足第2.1 小节所述的数理条件，即可求得对应的附加速度势。本文后续还将分别展示非刚性的自由液面、刚性角形壁面以及球形颗粒边界的镜像法应用案例。

3 水平壁面附近空化泡Kelvin 冲量

3.1 Kelvin 冲量计算

基于1.1 节中推导的Kelvin 冲量理论公式，Blake等[11,12]对水平壁面附近的空化泡Kelvin冲量进行了详细计算，并在考虑浮力作用的情况下，对空化泡Kelvin 冲量的方向进行了细致的定量分析。

根据式（9），空化泡所受Bjerknes 力还可表示为[11]

以x轴、y轴、z轴相互垂直建立直角坐标系，令x轴正方向为竖直向上，以表示水平方向的圆柱径向坐标。选择x=0平面作为控制表面Σb，则x方向上Bjerknes 力的表达式为[11]

式中：FΣx——Bjerknes 力在x方向上的分量；

ex——x方向的单位向量；

u——流体沿x轴方向速度；

v——流体沿径向方向的速度。

假设空化泡位于x=h、r=0处，可将其视为源强为m的点源，刚性水平壁面与x=0平面重合。根据镜像法原理，水平壁面对上半空间流场的作用可等效为在x=-h处添加一个源强同为m的点源。因此，上半空间流场的速度势为[11]

将以上两式代入式（45），可得x方向上Bjerknes力[11]

再考虑到浮力，空化泡在x方向上受力为[12]

值得注意的是，上述Bjerknes 力项与源强m的正负号无关，即该式对点源或点汇都适用，可以用来描述空化泡生长或溃灭时的情况[12]。

对于源强中的R˙项，可通过Rayleigh 泡动力学方程解得[12]

将式（50）、（51）与式（21）代入式（14）中，可得x方向的空化泡Kelvin 冲量为[12]

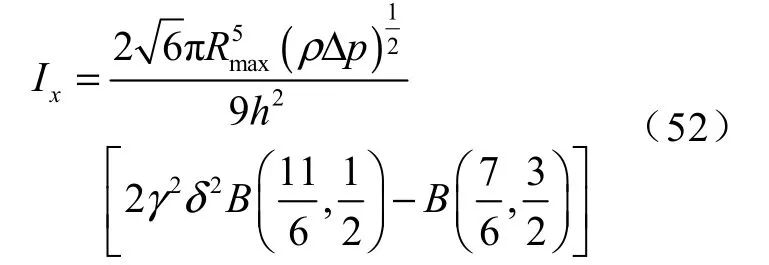
式中：γ——空化泡 -壁面间无量纲距离参数，

3.2 结果分析

Kelvin 冲量的符号和大小是非常有价值的参数，因为它决定了空化泡的射流方向、移动方向和溃灭的剧烈程度。根据式（52）可知，壁面附近空化泡的Kelvin 冲量大小取决于空化泡最大半径Rmax、流体密度ρ、无穷远处与泡壁处压力差Δp、空化泡 -壁面距离h等参数，而Kelvin 冲量的符号则取决于空化泡 -壁面间无量纲距离γ和无量纲浮力参数δ。令式（52）等于零，可得Kelvin 冲量为零的条件[12]

如图3 所示，在δ-γ图上画出了γδ=0.442的零Kelvin 冲量曲线，箭头表示基于边界积分法的数值计算所得的空化泡射流和移动方向。如果空化泡参数γδ＞ 0.442，空化泡射流方向将远离壁面；如果空化泡参数γδ＜ 0.442，空化泡射流方向将朝向壁面，这与基于边界积分法对空化泡射流和移动方向的数值计算结果相吻合[12]。

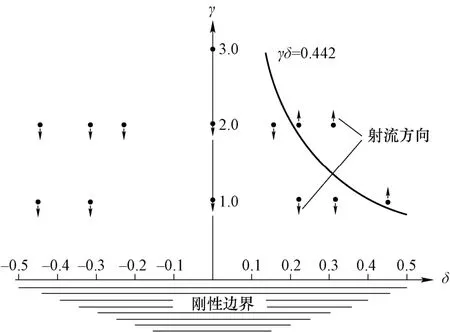
图3 不同γ和δ 参数下刚性水平壁面附近空化泡数值计算结果[12]Fig.3 Numerical results of cavitation near the rigid horizontal wall under different γ and δ parameters[12]

值得注意的是，Blake等[12,14]的计算还表明，当空化泡体积较小时，浮力作用并不明显。在可忽略浮力的情况下，空化泡只受Bjerknes 力的作用，Kelvin 冲量方向朝向刚性水平壁面，且空化泡 -壁面间距离越小，Kelvin 冲量的绝对值越大。

3.3 实验研究

Vogel等[17]通过高速摄影实验研究了刚性水平壁面附近激光空化泡的动力学特性及其与空化泡 -壁面间距离的关系。图4 为空化泡 -水平壁面间不同无量纲距离γ时的空化泡溃灭射流图像，其中每帧图像下方较暗的部分为水平壁面，子图（a）、（b）、（c）、（d）对应无量纲距离γ分别为2.3、1.56、0.75、0.34[17]。如图4 所示，溃灭时产生朝向壁面的射流是水平壁面附近空化泡动力学的主要特征。当空化泡相对远离水平壁面时，它在溃灭过程中向壁面移动，并形成朝向壁面的射流（子图a）。当空化泡 -壁面距离更近些时，溃灭过程中朝向壁面的射流更为明显，此外还出现了一个较小的反向射流（子图b）。随着空化泡 -壁面距离继续减小，溃灭过程明显变得更为剧烈，射流变得更厚，并在溃灭初期接触到了壁面（子图c、子图d）[17]。这与Blake等[12]的Kelvin 冲量理论所预测的情况一致。

图4 空化泡 -水平壁面间不同无量纲距离γ 时空化泡溃灭射流[17]Fig.4 The bubble collapse jet at different dimensionless distance γ between bubble and horizontal wall[17]

4 自由液面附近空化泡Kelvin 冲量

4.1 Kelvin 冲量计算

Blake等[11,13]对自由液面影响下的空化泡Kelvin 冲量进行了详细计算，并对无量纲距离和浮力参数对空化泡Kelvin 冲量方向的影响进行了定量分析。

令x轴正方向为竖直向下，假设空化泡位于x=h、r=0处，可将其视为源强为m的点源，自由液面与x=0平面重合。对于自由液面边界，与刚性壁面有所不同，其镜像法等效条件并非边界上法向速度为零，而是边界上速度势为零[11]。因此，自由液面对下半空间流场的作用可等效为在x=-h处添加一个源强为m的点汇。下半空间流场速度势为[11]

在自由液面x=0处[11]

将以上两式代入式（45），可得x方向上Bjerknes力[11]

再考虑到浮力，空化泡在x方向上受力为[13]

将上式代入式（14），可得x方向的Kelvin冲量为[13]

4.2 结果分析

对比式（49）与式（57）可知，对于刚性水平壁面边界，空化泡所受Bjerknes 力朝向壁面方向，而对于自由液面边界，空化泡所受Bjerknes 力朝向远离液面方向。

与刚性水平壁面附近的情况类似，自由液面附近空化泡Kelvin 冲量的符号也取决于空化泡 -壁面间无量纲距离γ和无量纲浮力参数δ。令式（59）等于零，即可得到Kelvin 冲量为零的条件[13]

如图5 所示，图中画出了γδ= 0.442的零Kelvin 冲量曲线，箭头表示基于数值计算或实验研究所得的空化泡射流和移动方向。如果空化泡参数γδ＞ 0.442，空化泡射流方向将朝向自由液面；如果空化泡参数γδ＜ 0.442，空化泡射流方向将朝向远离液面方向，这与射流方向的数值计算和实验结果基本吻合[13]。

图5 不同γ和δ 参数下自由液面附近空化泡数值计算结果[13]Fig.5 Numerical results of cavitation near the free surface under different γ and δ parameters[13]

4.3 实验研究

Bempedelis等[19]对空化泡与自由液面之间的相互作用进行了一系列实验研究，其重点在于深入探究空化泡在自由液面附近形成液体射流的模式和动力学。图6 为不同无量纲距离时空化泡溃灭和自由液面变形的阴影图，其中子图（a）、图（b）、图（c）所对应的空化泡 -液面无量纲距离γ分别为0.86、1.10、1.27，图像中间偏下处的水平黑线表示自由液面[19]。如图6 所示，空化泡在t= 0.1 ms 时达到最大尺寸，随后的溃灭过程呈现非球形。空化泡上端靠近自由液面的一侧被液体射流向下推入泡内，因此空化泡的上表面呈现平坦形状（子图a、子图b 的t= 0.15 ms 时刻）。溃灭过程中空化泡顶部被向下的液体射流击穿而呈现圆环状，在侧视图中看起来像一条粗线段（子图a、子图b 的t= 0.2 ms 时刻）。对比子图a 与子图b 可知，空化泡与液面距离更近时，溃灭过程更剧烈。在之后的阶段，空化泡在反弹、再溃灭或分离的过程中，会朝着液面的反方向移动（子图a、子图b 的t= 0.5 ms 时刻、子图c 的t= 0.4 ms时刻）[19]。此外，对于空化泡与自由液面相互作用研究，除了本文讨论的液面下方的射流情况外，自由液面上方产生的水冢现象等也是广受关注的内容，读者可参考Zhang等[30]的相关工作，本文不再展开赘述。

图6 不同无量纲距离时空化泡溃灭和自由液面变形的高速摄影图[19]Fig.6 High-speed photographs of bubble collapse and free surface deformation at different dimensionless distances [19]

5 角形壁面附近空化泡Kelvin 冲量

5.1 Kelvin 冲量计算

Tagawa 和Peters[18]在Blake 的Kelvin 冲量理论基础上，对多个角度的角形壁面附近空化泡Kelvin 冲量方向进行了计算，并通过实验测得空化泡射流方向，与计算结果进行了对比验证。

Tagawa 和Peters[18]在空化泡 -壁面模型的对称截面上计算Kelvin 冲量，用复数表示平面上的坐标以实现计算的简捷性。假设角形壁面的顶点与原点重合，水平壁面沿实轴正方向，另一个壁面与其夹角为α= πn。对于位于角形壁面内点的空化泡，以点源模型简化表示空化泡流场。根据镜像法原理，满足不可透壁面条件，角形壁面可等效为2n-1个虚拟汽泡点源（n为自然数），每个虚拟汽泡点源与角形壁面顶点的距离都为r0，其中，1 个虚拟汽泡点源的角度为(2π -θb)，n-1个虚拟汽泡点源的角度为(2πk-θb)，n-1个虚拟汽泡点源的角度为(2πk+θb)，k为从1 到n-1的自然数[18]。

根据Best 和Blake[15]的理论，Kelvin 冲量的方向取决于边界产生的附加速度势的梯度，即边界产生的附加速度。因此，每个虚拟汽泡点源在空化泡位置处产生的速度us的合速度方向即为空化泡Kelvin 冲量方向。单个虚拟汽泡点源在空化泡位置处的速度[18]

式中：us——单个虚拟汽泡点源在空化泡位置处的速度；

——虚拟汽泡点源位置向量rs的单位向量。

对于α= π的角形壁面，全部虚拟汽泡点源在空化泡位置产生的合速度[18]

式中：uj——全部虚拟汽泡点在空化泡位置产生的合速度；

C——常数项，

因此，Kelvin 冲量的角度为[18]

式中：θj——Kelvin 冲量角度；

Im(uj)——向量的uj虚部，即虚拟汽泡点源合速度的竖直方向分量；

|uj|——向量uj的模，即虚拟汽泡点源合速度的大小。

5.2 结果分析

根据计算过程可知，Kelvin 冲量的角度θ j只与空化泡位置角度θb有关，而与空化泡到角形壁面顶点的距离r0、空化泡最大半径Rmax等参数无关。对于不同角度的壁面，空化泡位置角度θb的范围为0到α，Kelvin 冲量的角度θ j的范围为0 到π-α，这意味着壁面角度α越小，射流角的范围就越大[18]。

为了统一、标准化地分析不同α时Kelvin冲量角度与空化泡位置角度间的关系，做如下无量纲处理[18]

式中：——无量纲空化泡位置角度；

——无量纲Kelvin 冲量角度。

图7 为不同壁面情况下无量纲射流角度与空化泡位置角度关系，六条曲线分别对应n=2、3、8、20、100、1 000 时的壁面情况[18]。如图6 所示，所有曲线都具有平滑的S 型形状，当和θˆb→1时，曲线的斜率，并且=0处的斜率随着n的增大而增大。当n→∞，即壁面角度α→ 0时，曲线会接近于一个阶跃函数。这种极限情况对应于两个平行壁面之间的空化泡，如果形成射流，则射流指向最近的壁面，而不是任何其他方向[18]。

图7 不同壁面情况下无量纲射流角度与空化泡位置角度关系[18]Fig.7 Relationship between dimensionless jet angle and bubble position angle under different wall conditions [18]

5.3 实验研究

Tagawa 和Peters[18]对α=π/2和α=π/3的角形壁面分别做了大量实验，研究空化泡射流角度与空化泡位置角度之间的关系，并将射流角度实验数据与Kelvin 冲量角度的计算结果进行对比验证。图8 为射流角度实验数据与Kelvin 冲量角度计算结果对比图，图中两条实线分别对应n=2、3时的Kelvin 冲量角度计算结果，空心圆形、实心正方形符号分别对应n=2、3 时的射流角度实验数据[18]。如图8 所示，射流角度实验数据与Kelvin冲量角度计算结果基本一致，因此基于势流理论计算的Kelvin 冲量方向，能够准确地预测空化泡溃灭时产生的射流方向[18]。

图8 射流角度实验数据与Kelvin 冲量角度计算结果对比图[18]Fig.8 Comparison between experimental data of jet angle and calculation results of Kelvin impulse angle[18]

6 球形颗粒附近空化泡Kelvin 冲量

6.1 Kelvin 冲量计算

Best 和Blake[15]基于简化的Kelvin 冲量计算方法，对刚性球形颗粒附近空化泡Kelvin 冲量进行了计算与分析。

假设在三维直角坐标系中，一个无量纲半径为a的刚性球形颗粒固定在原点处，源强为m的空化泡位于r0=(0,0,ξ)处。根据镜像法中的Weiss 球定理[31]，该球形颗粒对流场的影响可等效于一个位于 (0,0,a2/ξ)处的源强为ma/ξ的虚拟汽泡点源，和一个从坐标原点到(0,0,a2/ξ)点的源强密度为m/a的均匀线性汇，如图9 所示。具体而言，根据Weiss 球定理可知球形颗粒产生的附加速度势φ′为[15]：

图9 Weiss 球定理镜像法示意图[15]Fig.9 The schematic of the mirror image method of Weiss ball theorem[15]

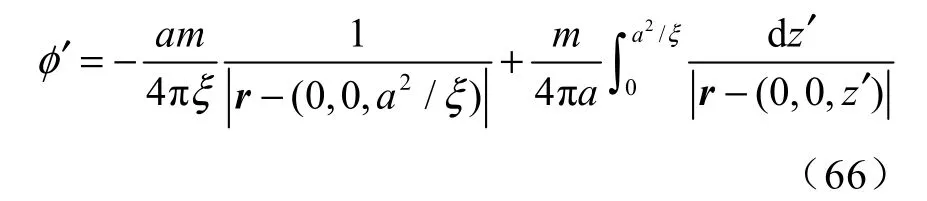
式中：r——表示流场中某点坐标，r=(x,y,z)；

z′——积分变量，无物理意义。

将式（23）与式（66）联立可得[15]

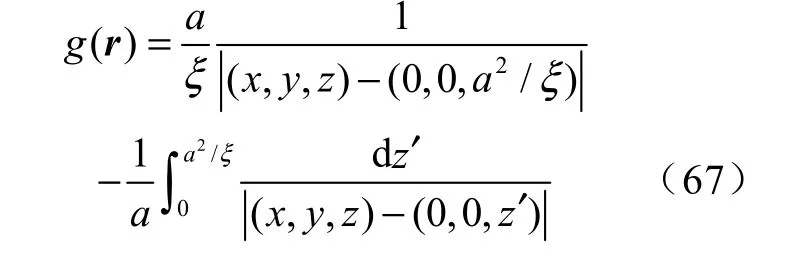
将式（67）代入式（25）、（29），并令r=r0可得[15]

式中：er——指向球形颗粒中心的方向向量。

将式（68）、（69）代入式（35）、（36）即可求得Kelvin 冲量。

6.2 结果分析

通过上述公式，Best 和Blake[15]计算了考虑浮力作用下的球形颗粒附近空化泡Kelvin 冲量，并分析了颗粒附近各点处的Kelvin 冲量方向。

定义一个围绕球形颗粒的临界表面Sa，在此临界面上任意点处的空化泡Kelvin 冲量方向与球形颗粒相切。那么在这个临界面以内颗粒的Bjerknes 力对空化泡吸引作用足够大，以至于最终Kelvin 冲量方向指向颗粒，相反在临界面Sa以外的区域空化泡Kelvin 冲量方向将远离颗粒。因此将面Sa内的区域定义为“吸引区”[15]。

图10 为无量纲半径a=2的球形颗粒周围吸引区示意图，其中空化泡的无量纲浮力参数δ= 0.1[15]。如图9 所示，吸引区表面Sa的上半部分近似均匀地包围着颗粒，当z→∞时，吸引区表面Sa在x-y坐标面上的投影近似与颗粒投影重合。这是因为当z→∞时，颗粒对空化泡的Bjerknes吸引力趋于零，颗粒下方的空化泡主要受浮力作用，产生竖直向上指向颗粒的Kelvin 冲量[15]。

图10 无量纲半径a=2的颗粒周围吸引区示意图[15]Fig.10 The schematic of attraction area around spherical particles with dimensionless radiusa=2[15]

6.3 实验研究

Zhang等[21]通过高速摄影实验研究空化泡与球形颗粒的相互作用，对空化泡尺寸、颗粒尺寸以及空化泡 -颗粒间距离的变化进行了一系列的研究。

图11 为不同无量纲距离下颗粒附近空化泡动力学的实验图像[21]。当空化泡 -颗粒无量纲距离较小时，空化泡在溃灭期间将呈蘑菇型。由于空化泡与颗粒紧密接触，在射流形成过程中，空化泡将分为两部分：一部分靠近颗粒、一部分远离颗粒（子图a）。当空化泡 -颗粒无量纲距离中等时，空化泡在溃灭期间将呈梨形。在射流形成过程中，空化泡中间区域被击穿，在侧视图中表现为对称地分成两部分（子图b）。当空化泡 -颗粒无量纲距离较大时，在射流形成过程中，空化泡仍保持近似球形。与前两种情况相比，此时微射流强度要弱得多。随后空化泡的反弹和二次溃灭过程也近似球形，并朝向颗粒轻微移动（子图c）。可以预见，随着γ值的增大，颗粒的影响将逐渐减小直至消失[21]。

图11 不同无量纲距离颗粒附近空化泡动力学实验图像[21]Fig.11 Experimental images of cavitation dynamics near particles at different dimensionless distances[21]

图11 不同无量纲距离颗粒附近空化泡动力学实验图像[21]（续）Fig.11 Experimental images of cavitation dynamics near particles at different dimensionless distances[21]

除颗粒或壁面的单一边界外，Zhang等[22,23]还研究了颗粒与壁面复合边界与空化泡相互作用情况，通过详实的高速摄影实验数据，探究了空化泡、颗粒和壁面间的相对位置对空化泡溃灭形态、射流行为的影响。基于微射流方向的不同，将颗粒与壁面间的空化泡溃灭行为定量划分为三种情况，并揭示了其主要特征。图 12 为不同空化泡 -颗粒无量纲距离γp和空化泡 -壁面无量纲距离γw下，颗粒和壁面之间空化泡动力学实验图像[22]。情况1 对应空化泡距离颗粒较远、距离壁面较近时，溃灭时产生朝向壁面的射流，并且空化泡朝壁面方向移动（子图a）。情况2 对应空化泡距离颗粒和壁面都较近时，溃灭过程中空化泡主体朝向壁面移动，但其与颗粒下表面保持接触。溃灭后期空化泡分裂为两部分，一部分产生朝向颗粒的射流，另一部分产生朝向壁面的射流（子图b）。情况3 对应空化泡距离颗粒较近、距离壁面较远时，空化泡溃灭时产生朝向颗粒的射流（子图c）[22]。

张湘晴和张宇宁[23]利用240 000 帧/秒的高速相机对颗粒与壁面复合边界附近的空化泡射流角度及其移动进行了定量分析。图13 为颗粒和壁面附近空化泡溃灭射流实验图像，其中球形颗粒与空化泡中心保持水平且均位于固体壁面上方。如图13 所示，空化泡溃灭时产生朝向壁面的细长射流，并在一定程度上向颗粒方向倾斜[23]。图14 为射流角度θ随无量纲参数α0的变化规律。其中，无量纲参数α0为空化泡 -颗粒无量纲距离与空化泡 -壁面无量纲距离间的比值，表征空化泡在固体壁面与颗粒附近的相对位置。如图14 所示，随着α0的增大，射流角度θ呈减小趋势，说明颗粒对空化泡的影响越来越小，壁面对空化泡的影响越来越趋于主导作用[23]。由于壁面的影响，空化泡在溃灭过程沿颗粒表面向下发生显著的移动，如图15 所示，无量纲参数α0越大，空化泡在颗粒表面的移动弧度β越大[23]。