基于增量模型切换和反步控制法的船舶主动升沉补偿策略

张 琴，张蒸忠，刘敦康，董慧芳，胡 雄

(上海海事大学 物流工程学院，上海 201306)

0 引 言

面对双碳目标对于能源革命的新要求，我国政府发布了《中国制造2025-能源装备实施方案》，以能源装备推动关键风电装备和技术的发展。随着海上风电设备功率的增大，体积质量也随之增长，对海上风电设备安装时的精准性和安全性要求也越来越高。海上风电设备通过浮式起重船运载安装，而不规则波浪运动会造成浮式起重船的晃动，影响海上风电设备安装时的精准性和安全性。因此，波浪补偿对海上风电的精准安装来说极其重要，且对于加快海上风电远洋建设也有着重要的意义。

波浪补偿相关技术在国内外已有大量研究。浮式起重船通常采用绞车恒张力补偿和随动补偿技术，能够保证所提货物及补给船的安全，常用于解决海上船舶补给吊装的问题，但此类起重机难以达到对风机安装时的精度要求。文献[4]提出了一种基于液压阀主动升沉补偿系统的ADRC-ESMPC双环控制器。文献[5]基于奇异摄动理论开发了液压主动升沉补偿器系统的控制算法。振华重工基于二次控制液压马达研发的主动式甲板起重机升沉补偿系统。液压缸有着动力大、应用广等优点，但液压缸行程和传动效率不高，导致补偿范围不足，补偿时延较大。

为了提高升沉补偿的控制精度及行程，本文采用六自由度波浪补偿电缸控制系统平台进行试验，电缸的位置精度控制可以达到0.01 mm，且传动效率为90%，能精确实时控制。但当电缸动作位移不同时，电缸动作的响应时间和电缸控制系统的时延也会改变，导致补偿控制时的滞后现象。由于反步法控制能完成高精度的补偿，适用于状态线性化或具有严参数反馈的不确定非线性系统。因此，本文采用基于增量模型切换和反步控制策略对电缸主动升沉补偿系统进行补偿控制。

1 电缸主动升沉补偿系统及控制流程

采用六自由度波浪补偿电缸控制系统平台开展试验。系统由下平台和上平台两部分构成，下平台为六自由度波浪模拟平台，用来模拟实际船舶升沉运动；上平台为用于波浪补偿的电缸控制系统，由工控机和电缸驱动补偿系统组成，电缸驱动补偿系统包括运动控制卡、伺服驱动器、电缸执行机构。通过工控机控制电缸动作，补偿下平台的升沉运动，并通过激光传感器检验补偿精度。

电缸主动升沉补偿系统的流程如图1所示，主要分为3个阶段：

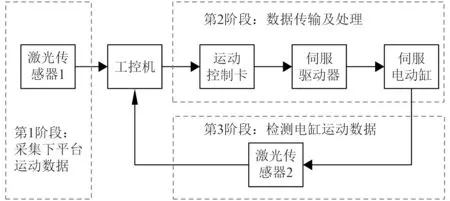
图1 电缸主动升沉补偿系统流程图Fig. 1 Flow chart of electric cylinder active heave compensation system

1）利用具有高精准性的激光传感器1采集下平台模拟的波浪数据，同时传输到工控机中。由此可以精确的检测到下平台的升沉位移信号。

2）在工控机上编写C#语言控制策略算法程序，通过PCI总线传输到运动控制卡上。运动控制卡接受指令并向伺服驱动器发送指令，使伺服驱动器带动电缸运动，以此补偿下平台的升沉位移。

3）由激光传感器2检测电缸的补偿运动，得到补偿位移数据再传回工控机来检测补偿精度，形成补偿控制的闭环，进一步调整控制策略。

由于数据采集和运动控制在数据传输时会产生时延，且在不同位移输入下的电缸动作会产生不同的时延，这些时延会造成系统控制效果变差甚至失稳，所以使用常规机理法建立的电缸数学模型已无法满足系统补偿控制精度要求，因此研究在不同升沉位移输入下的电缸时延问题，并建立系统的模型，以达到系统高精度的补偿。

2 电缸驱动补偿系统建模

在第2阶段（见图1）中，电缸驱动补偿系统补偿控制时包括工控机传输数据、运动控制卡接受与发送指令、电缸动作等3个部分。由于常规机理法建模无法体现数据传输时的时延，故采用基于阶跃位置响应的试验建模方法。本预设置下平台单步位移数据分别为1 mm，5 mm，9 mm的3组信号，由工控机传输信号，直到让电缸响应动作。同时由激光传感器检测电缸的3组动作信号，可得到电缸的动作响应曲线，如图2所示。

由图3发现具有纯滞后的一阶惯性特性，辨识得到模型为：

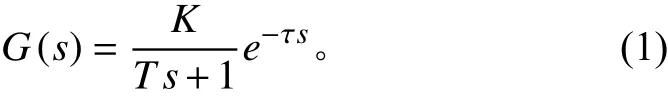
式中：为增益值，为时间常数， τ=τ+τ为总时延；τ为 伺服电机驱动电缸动作的时延，τ为第2阶段中数据的传输时延，在此系统中可认为τ不变。

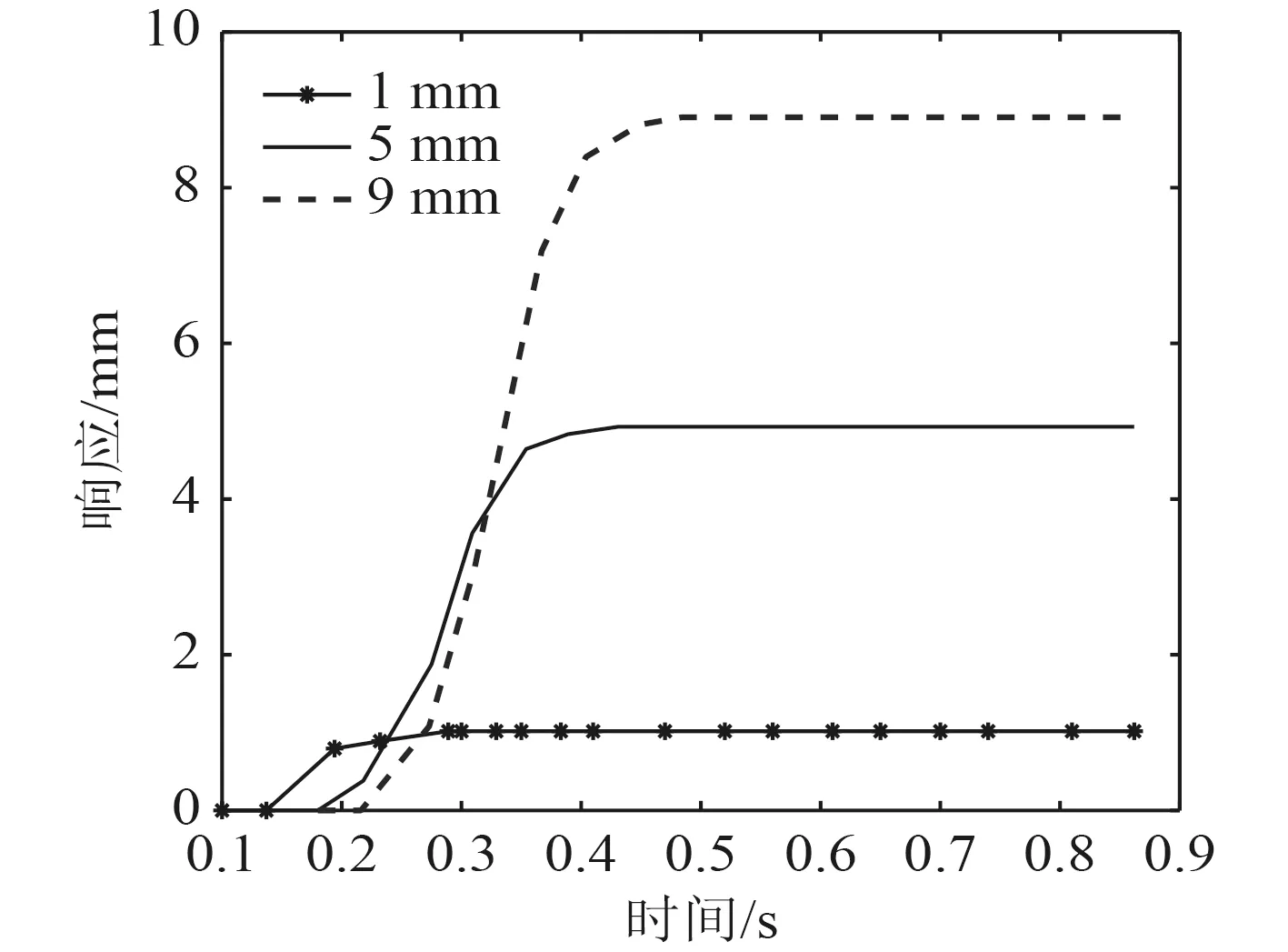
图2 电缸驱动补偿系统响应曲线Fig. 2 Step response curve of electric cylinder drive compensation system

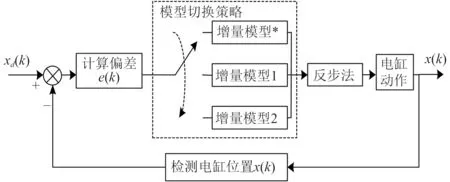
图3 基于增量模型切换的反步法控制策略Fig. 3 Back stepping control strategy based on incremental model switching

结合图2和式（1），进一步计算得到3条位置响应曲线的时间常数，延时 τ和增益值，如表1所示。

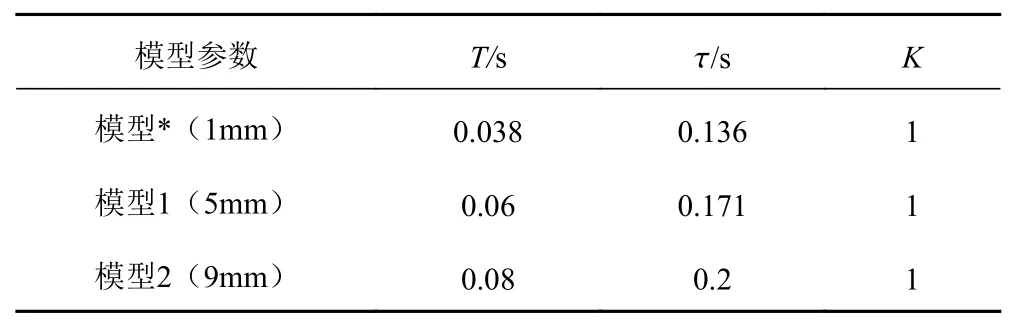
表1 电缸驱动补偿系统响应计算值Tab. 1 Response calculation value of electric cylinder drive compensation system

表1中，模型*中的参数为1 mm的响应计算值，因1 mm的位移非常小，所以可忽略电缸中伺服电机动作的时延，即τ= 0，数据传输时延τ=0.136 s。而表1 3个模型中的参数和τ 减去τ后的数值不一样，由此可见时间常数和延时τ会随着下平台的升沉位置控制信号的不同而改变，即补偿系统模型是不固定的。

研究发现，模拟的波浪运动相邻位置差 Δx()在1～9 mm之间，为了能让电缸快速补偿下平台目标位置，补偿电缸采用位置增量控制方式。即电缸每次动作的位移数据为前一时刻的增量位移，此控制方式能保证电缸响应的快速性。将测得的下平台当前位移x() 和上一时刻的位移x(-1)数据传输给工控机，经计算得到 Δx()=x()-x(-1)，即为电缸的补偿增量。但每次测得的补偿增量 Δx()都不同，故电缸补偿动作 Δx()的时延也不相同，因此表1中的3个模型可以视为相应补偿增量 Δx()的增量模型。针对不同波浪运动位置增量，采用增量模型切换策略驱动电缸补偿动作，实现对下平台波浪运动的补偿控制。

3 基于增量模型切换的反步法控制策略

针对上述非线性模型，采用反步法实现电缸主动升沉补偿系统的稳定控制，而由于系统时延的时变原因，固定模型的控制器已无法满足此系统的精度要求，设计基于增量模型切换的反步法控制策略，如图3所示。

下平台的模拟波浪运动相邻数据位置差在1～9 mm之间，因此增量模型1可较为直观表现整个系统，在系统补偿精度要求不高的情况下，增量模型1能满足时变时延的精度要求，而增量模型切换策略可保证系统硬件更高的补偿精度。因此在图3中，系统开始时选用增量模型1作为初始模型进行补偿控制，由工控机计算得到当前时刻下平台位置x()与电缸位置()之间的偏差()，通过辨别偏差()是否满足系统的精度要求，选择是否切换其他增量模型，切换增量模型改变补偿时延，以达到更高的补偿精度。在浮式起重船不同的工作状态下，对补偿精度有着不同的要求，对于海上浮式起重船的一般工作情况下，补偿精度在70%以上就能满足浮式起重船的稳定航行，本文()设定为不能超过当前海况波浪幅值的30%。

针对确定好的实时增量模型，采用反步法进行补偿控制，可设计满足Lyapunov定律的标量函数和中间虚拟控制量，进而反推到整个系统以完成控制律的设计。通过反向设计使控制标量函数和控制器的设计过程系统化、结构化，适用于具有严参数反馈的不确定非线性系统，也可以用来控制阶的非线性系统。

控制器设计具体步骤如下：

将式（1）转化为状态空间方程，可以得到如下离散系统：

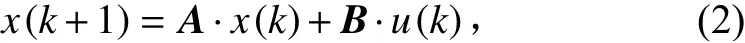
式中：为表1中3个模型转换后得到的系数矩阵，=1， 系统需要跟踪的下平台位移值为x()，则令电缸系统的当前时刻位移跟踪误差为：

依据误差()趋向于0的目的，设计李雅普诺夫函数为：

此时有()≥0，对式（4）函数求差分可得：

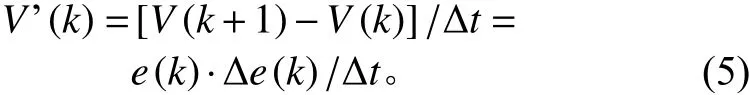
式中：

为了保证系统的稳定性，李雅普诺夫第二方法要求Δ()≤0，故令

可满足:

将式（3）和式（6）代入式（7）可以得到：

() 即为该控制器的控制律。显然当()≠0时，()=1/2·()＞0 ，Δ()=-()＜0，故满足李雅普诺夫第二方法要求，可知控制律的设计满足电缸主动升沉补偿系统的稳定性要求。

综上，基于增量模型切换的反步法控制策略，电缸动作能够快速、稳定、精准地跟踪补偿下平台模拟波浪位移，能够有效提高风电叶片安装时的效率及安全性。

4 基于电缸主动升沉补偿平台的试验结果

通过电缸主动升沉补偿系统试验平台验证基于增量模型切换的反步控制策略有效性。为了验证增量模型切换反步控制策略在四五级海况下的补偿效果，现取不同波浪周期和幅值进行试验。但波浪起伏高度通常在几米甚至几十米，在实验室内无法复现该波浪运动。因此，将波浪的幅值和周期以一定比例缩小得到下平台的模拟波浪数据。取3组数据做试验，试验1：幅值'=31.8 mm，周期'=8 s；试验2：幅值'=40 mm，周期'=8 s；为了不失一般性，试验3：取不同波浪幅值进行试验，幅值'=31.8 mm，40 mm，周期'=10 s。为了验证增量模型切换反步控制策略的优越性，与单模型（增量模型1）反步控制做对比试验，试验结果如图所示。

由图4可以看出，单模型补偿控制方法在电缸持续补偿动作一段时间之后的误差值较大，且有相位超前现象产生的误差。随着图5波浪幅值的增大，补偿误差也随之增大。在图6中当波浪运动幅值变化时，单模型补偿控制方法在波浪幅值变化的地方难以较快地跟踪补偿，尤其在波峰波谷处的偏差较大，随着时间变化电缸的位移偏差还会越来越大。由此可见，在实际补偿系统中，单一模型无法快速准确地跟踪波浪运动，不能满足时变时延系统的运动要求。由图可知，采用基于增量模型切换的反步控制策略时，在波峰波谷处能更好的跟踪补偿，并在波浪幅值变化时也能快速准确地跟踪船舶位移，补偿精度高于单模型补偿控制，补偿精度基本达到时变时延系统的要求。由表2均方根误差（RMSE）可见，基于增量模型切换的反步控制策略在试验1中误差降低了50%，试验2中误差降低了67%，试验3中误差降低了50%，补偿精度均在80%以上，提高了电缸主动升沉补偿系统的控制精准性和快速性，能有效满足海上风电设备安装时的效率及安全性。

图4 试验1中模型切换与单模型的补偿效果对比图Fig. 4 Comparison of compensation effect between model switching and single model in test 1

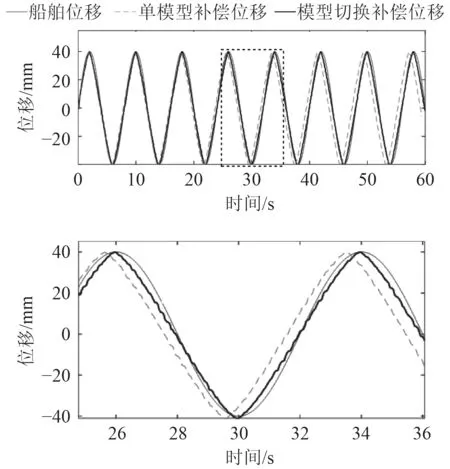
图5 试验2中模型切换与单模型的补偿效果对比图Fig. 5 Comparison of compensation effect between model switching and single model in test 2

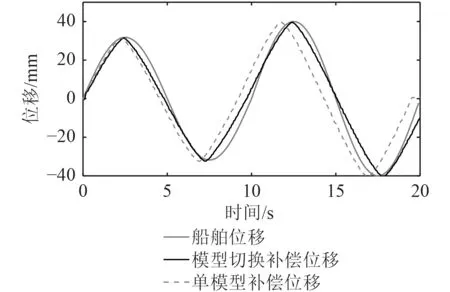
图6 试验3中模型切换与单模型的补偿效果对比图Fig. 6 Comparison of compensation effect between model switching and single model in test 3

表2 位移偏差的均方根误差（RMSE）Tab. 2 Root mean square error of displacement deviation (RMSE)

5 结 语

为保证海上风电设备安装时的精准性及稳定性，本文提出基于增量模型切换和反步控制法的船舶主动升沉补偿策略。针对电缸主动升沉补偿系统中存在的时变时延问题，通过阶跃位置响应的实验建模方法建立了不同位移下的电缸主动升沉补偿系统数学模型，并依据补偿的位移偏差来切换系统的增量模型，最后采用反步法对船舶运动进行补偿控制。电缸主动升沉补偿系统试验结果表明，本文策略对电缸补偿控制系统有良好的补偿效果，可以保证系统高精度快速稳定地跟踪补偿波浪运动，提高了主动式升沉补偿系统的性能。