非正弦升沉运动下串列水翼推进性能研究

李光钊，常 欣，邓南彦，于鹏垚

(大连海事大学 船舶与海洋工程学院，辽宁 大连 116026)

0 引 言

在自然界中，蜻蜓、蜜蜂等昆虫的扑翼结构是最常见的串列扑翼系统，学者们从中获得灵感，采用多翼串列的方式来提升扑翼系统的推进性能。于宪钊等分析了前翼拍动后翼静止的串列翼系统水动力；Jones等分析了串列水翼的推进性能并进行了相关试验研究；Broering等采用数值模拟方法研究了串列扑翼的气动力性能；石成明等采用气动力试验方法研究了串列翼型所产生的推力与前后翼距离之间的变化规律；李永泽等研究了3种串列双翼的气动布局，分析了最优的前后翼布局方案。许国冬等针对典型推进运动模式与能量采集模式，分析了串列双翼之间涡的干扰规律。

尽管国内外针对串列翼的气动力和水动力性能已开展许多研究，但过往研究中的串列翼运动形式大多为正弦运动。自然界生物的扑翼运动轨迹往往是更为复杂的非正弦运动，目前尚未看到针对非正弦运动串列水翼推进表现的研究。在串列扑翼式水下航行器的研发驱动下，本文采用计算流体力学方法研究非正弦升沉运动下串列水翼的推进性能，为水下航行器的扑翼运动模式选择提供指导。

1 计算方法

1.1 扑翼运动的描述

本文中非正弦运动通过椭圆形轨迹实现，其中，扑翼的升沉运动位移方程定义如下：

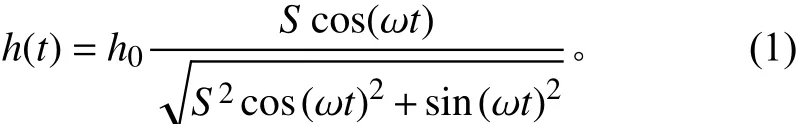
其中：为扑翼升沉运动的非正弦参数；为升沉运动幅值； ω=2π，为拍动频率；为时间。=1时，扑翼运动即为正弦运动，不同值对应的扑翼运动轨迹如图1所示。

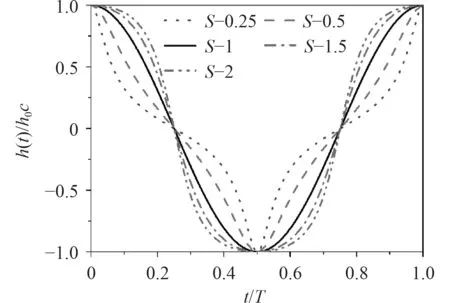
图1 不同S值的扑翼运动轨迹Fig. 1 Flapping trajectories according to different values of S

当两扑翼前后串列排布时，前翼和后翼的升沉运动可分别表示为：

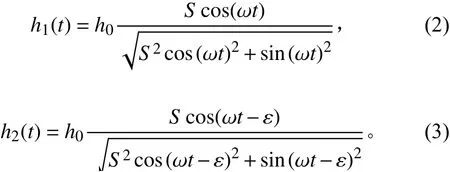
其中：()为串列排布两翼中前翼的运动方程，()为后翼的运动方程；为扑翼升沉运动非正弦参数；为前后两翼升沉运动的相位差。

图2 串列水翼布置图Fig. 2 Layout of in-line tandem hydrofoils

1.2 物理量的定义

扑翼在运动时会受到不同方向上的水动力和水动力矩。本文对串列翼系统的前后水翼力学特性分别讨论，作用在单独进行升沉运动水翼上的瞬时推力系数C和瞬时升力系数C可表达为：

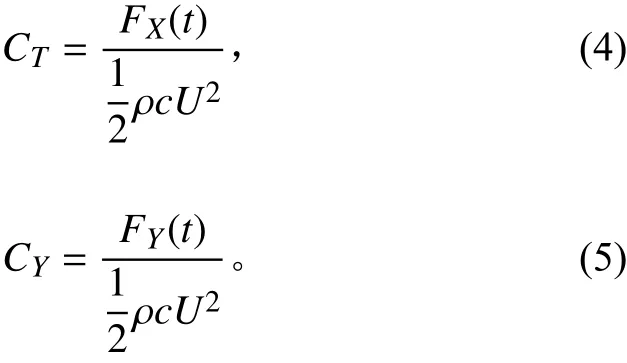
其中：F()为作用在单独水翼上沿轴的瞬时推力；F()为作用在单独水翼上沿轴的瞬时升力；为流体的密度；为流场来流速度。

则平均推力系数C和平均功率系数C可表达为：

其中：为扑翼升沉运动周期；P为扑翼运动时所需功率。

对于升沉运动水翼，一个运动周期所需的功率可以通过下式计算：

其中：为水翼沿轴轴向速度。

单独水翼的推进效率 η可表达为：

1.3 数值方法与计算模型

本文采用基于有限体积法的商用CFD求解器STAR-CCM+进行串列水翼的水动力分析。其中，水翼的运动利用重叠网格技术来实现。数值模型的计算域如图3所示，其中，分析的水翼为NACA0012标准翼型，翼弦长=0.1 m。方形区域为背景域，尺寸设置为70×70；中间圆形区域为重叠域，半径为1。根据Chao等的研究，当扑翼和计算域边界的距离大于20时，流域尺寸对水翼水动力的影响可以忽略不计，因此，可以判断本文中的计算域尺寸已足够大。具体的计算域边界条件如图3所示。

图3 串列双翼计算域及边界条件Fig. 3 The domain and boundary conditions of in-line tandem hydrofoils

1.4 数值收敛性分析

性分析，具体计算参数取值为=0.7，=1×10，=0.35 ，=0.25 ，相 位 差 ε=0 。其 中，为雷诺数，其定义为：

针对数值模型中的时间步长和网格尺寸进行收敛

式中：为来流速度，为水的动力粘度。为斯特劳哈尔数，反映流体非定常运动的相似性，其定义为：

式中，为运动频率。

图4 不同时间步长下瞬时推力系数时历曲线Fig. 4 Time history of instantaneous thrust coefficient of in-line tandem flapping foil under different time steps

图5 不同网格下的瞬时推力系数时历曲线Fig. 5 Time history of instantaneous thrust coefficient of in-line tandem flapping foil under different grids

图4为不同时间步长下前后水翼推力系数时历曲线的比较。计算中选取的时间步长分别为d=/1 000，/2 500，/4 000，对应计算模型的网格数目为24.5万。可以看出，不同时间步长下水翼的推力曲线吻合较好，故时间步长d=/2 500用于后续计算。图5为不同网格密度下前后水翼推力系数时历曲线的比较。对应3个不同的网格密度，扑翼表面分别具有200，400，600个节点，对应计算模型的网格数目分别为6.8万、24.5万和54.1万，计算中采用的时间步长d=/2 500。可以看出，不同时间步长下水翼的推力曲线总体吻合较好，表明当前数值模型具有较好的网格收敛性，在后续计算中选取网格数目为24.5万的计算模型。

1.5 数值算法的验证

图6为本文数值结果与Heathcote等试验结果以及Y.L.Wang等和Young等数值结果的对比。其中，计算翼型为NACA0012水翼，弦长=0.1 m，雷诺数=2×10，运动幅值=0.175，水翼运动形式为单翼的正弦纯升沉运动。横坐标为无量纲所减频率，定义为=2π/。可以看出，本文数值结果与文献[9]试验结果吻合较好。图7为本文数值结果与Kinsey等结果的对比。其中，文献中的计算结果也被许国冬等采用，用于验证数值模型。其中，计算翼型为NACA0015水翼，弦长=0.1 m ，雷诺数=2×10，运动幅值=1.0，水翼运动形式为串列水翼的俯仰升沉复合运动。可以看出，本文数值结果与文献数值结果吻合较好。总体而言，当前数值方法在本文中的应用是合理可行的。

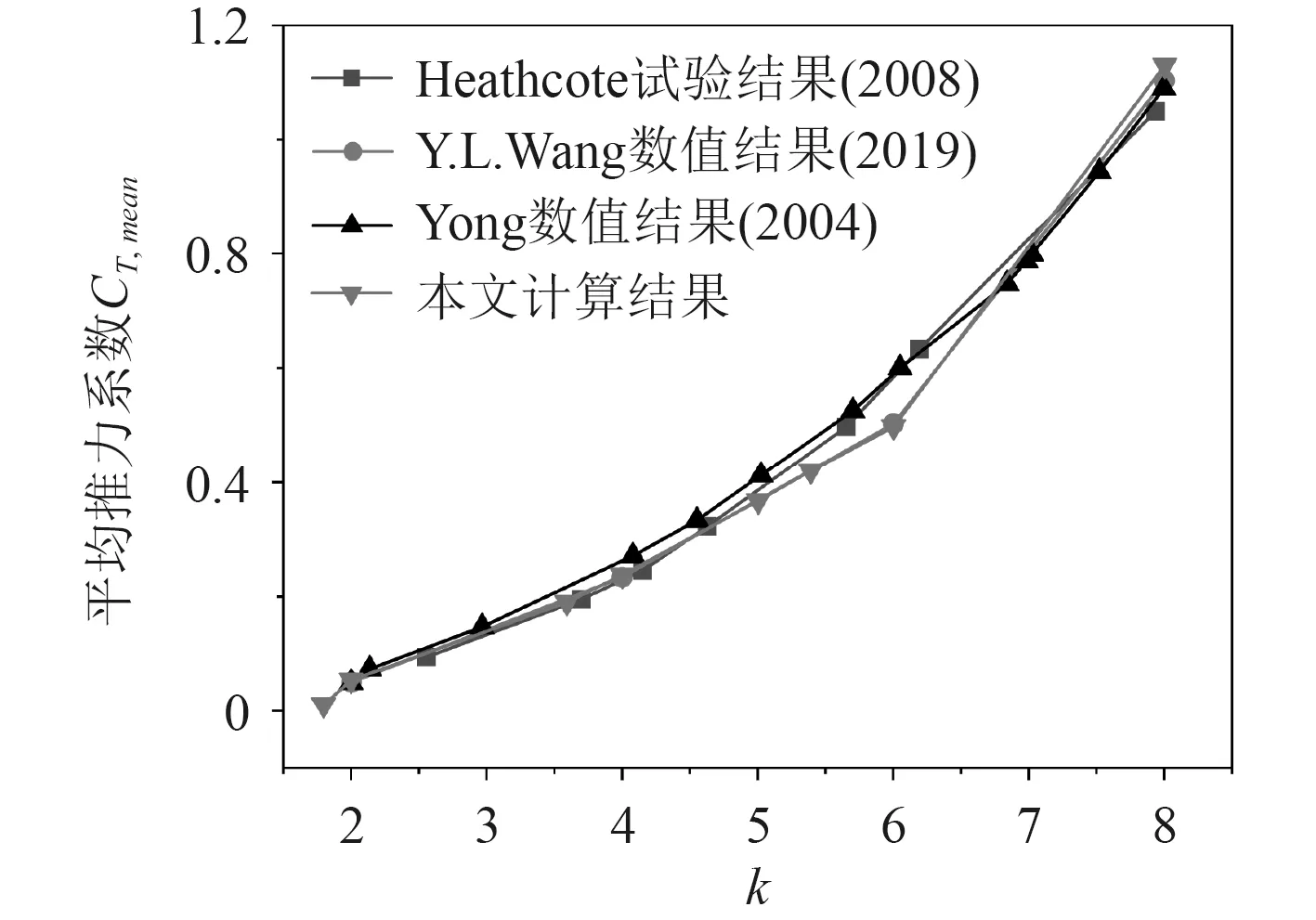
图6 单翼升沉运动验证Fig. 6 Plunge motion verification of single hydrofoil

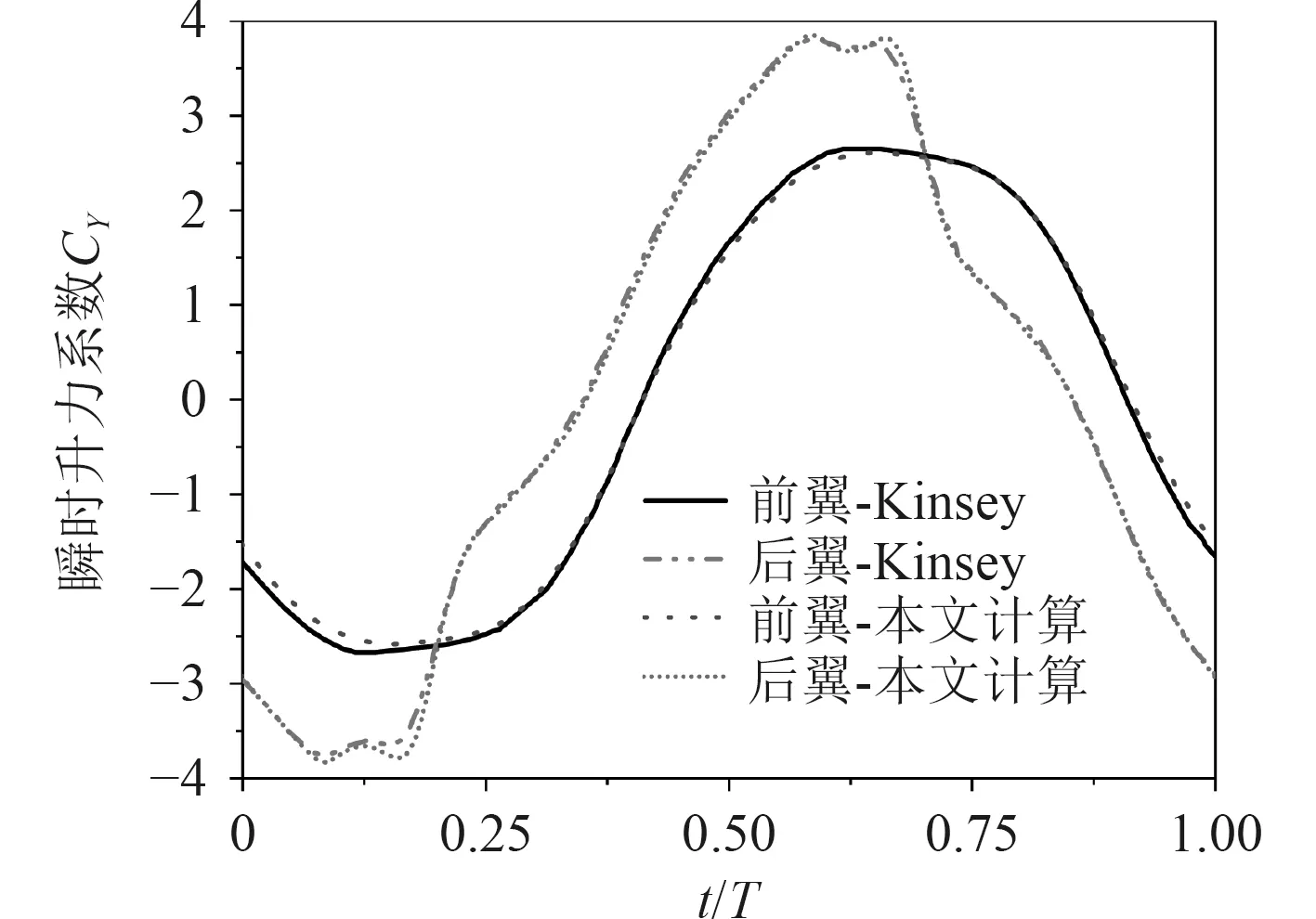
图7 串列双翼复合运动验证Fig. 7 Combined motion verification of in-line tandem hydrofoils

2 结果与分析

主要讨论非正弦运动对串列升沉水翼推进性能的影响，其中无特殊说明，计算参数=0.7，=1×10，=0.35，L=7.5，保持不变。

2.1 非正弦升沉系数S对瞬时水动力的影响

采用前后翼相位差 ε=90的结果进行分析。如图8（a）所示，对于前翼的瞬时推力系数曲线：从峰值来看，非正弦系数从=1增大或减小，都会使前翼瞬时推力系数曲线峰值增加；从周期来看，增大非正弦系数时周期基本不变，而减小非正弦系数时原有周期发生变化，峰值出现位置由水翼运动的平衡位置（0.25、0.75）变化为水翼运动的极端位置（0、0.5、1）。如图8（b）所示，对于后翼的瞬时推力系数曲线：从峰值来看，随着非正弦系数的减小，后翼推力系数曲线峰值增大，随着非正弦系数的增大，峰值先减后增；从周期来看，由于相位差的存在，后翼周期应比前翼推迟0.25，而当=1时，峰值却提前出现，这是前翼的尾流作用所致。

图8 不同非正弦系数下串列扑翼的瞬时推力系数时历Fig. 8 Time history of instantaneous thrust coefficients of in-line tandem flapping foils under different non-sinusoidal coefficient

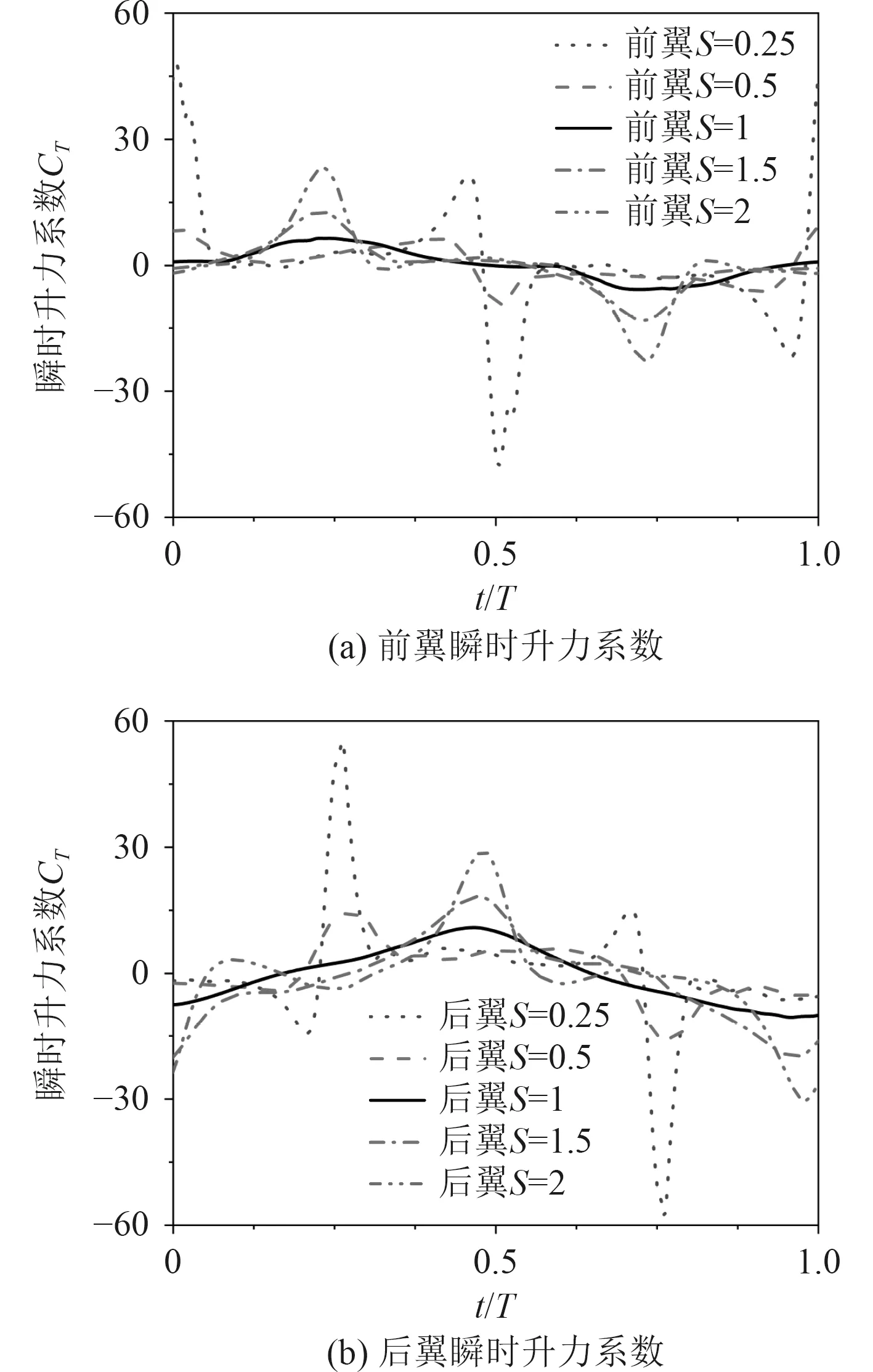
图9 不同非正弦系数下串列扑翼的瞬时升力系数时历Fig. 9 Time history of instantaneous lift coefficients of in-line tandem flapping foils under different non-sinusoidal coefficient

如图9（a）所示，对于前翼的升力系数曲线：从峰值和谷值来看，从=1增大或减少非正弦系数均可增大或减小升力系数曲线的峰值或谷值，且从=1减小时相比于增大时峰值增大或谷值减小的程度更大；从周期来看，当＞1时周期基本不变，而当＜1时，峰值或谷值出现位置由水翼运动的平衡位置（0.25、0.75）变化为水翼运动的极端位置（0、0.5、1）。如图9（b）所示，对于后翼的瞬时升力系数曲线：从峰值和谷值来看，从=1增大或减小非正弦系数同样会使升力系数曲线峰值更大，谷值更小；从周期来看，由于相位差的存在，后翼的周期性变化比前翼慢0.25。

2.2 非正弦升沉系数S对涡结构的影响

图10和图11分别为前后两翼在=0.5时刻不同非正弦升沉运动时周围流场的涡量云图。此时前翼处于最大负向位移位置，后翼处于向下运动的平衡位置。将水翼的上表面称为吸力面，下表面称为压力面，水翼形成升力的原因是吸力面与压力面的压强差。

前翼在非正弦系数=1时，一组尾涡由2个正向旋转、1个负向旋转的涡组成。在脱落过程中，正向旋转的涡迅速变弱至消失。水翼首部有一对旋向相反的涡，且带着一个未与水翼表面接触的负向旋涡。当这组涡向水翼尾部运动时，涡强度逐渐减弱。由于上表面的涡弱，上下表面压力差不大，升力无明显变化。当＜1时，尾涡组成与=1时相似，当减小时，尾涡中一个正向旋转的涡强度增强，推力明显增大。当＞1时，一组尾涡由2对旋向相反的涡组成，且脱落后负向旋涡迅速减弱，当增大时，上表面脱落的负向旋涡强度增大。

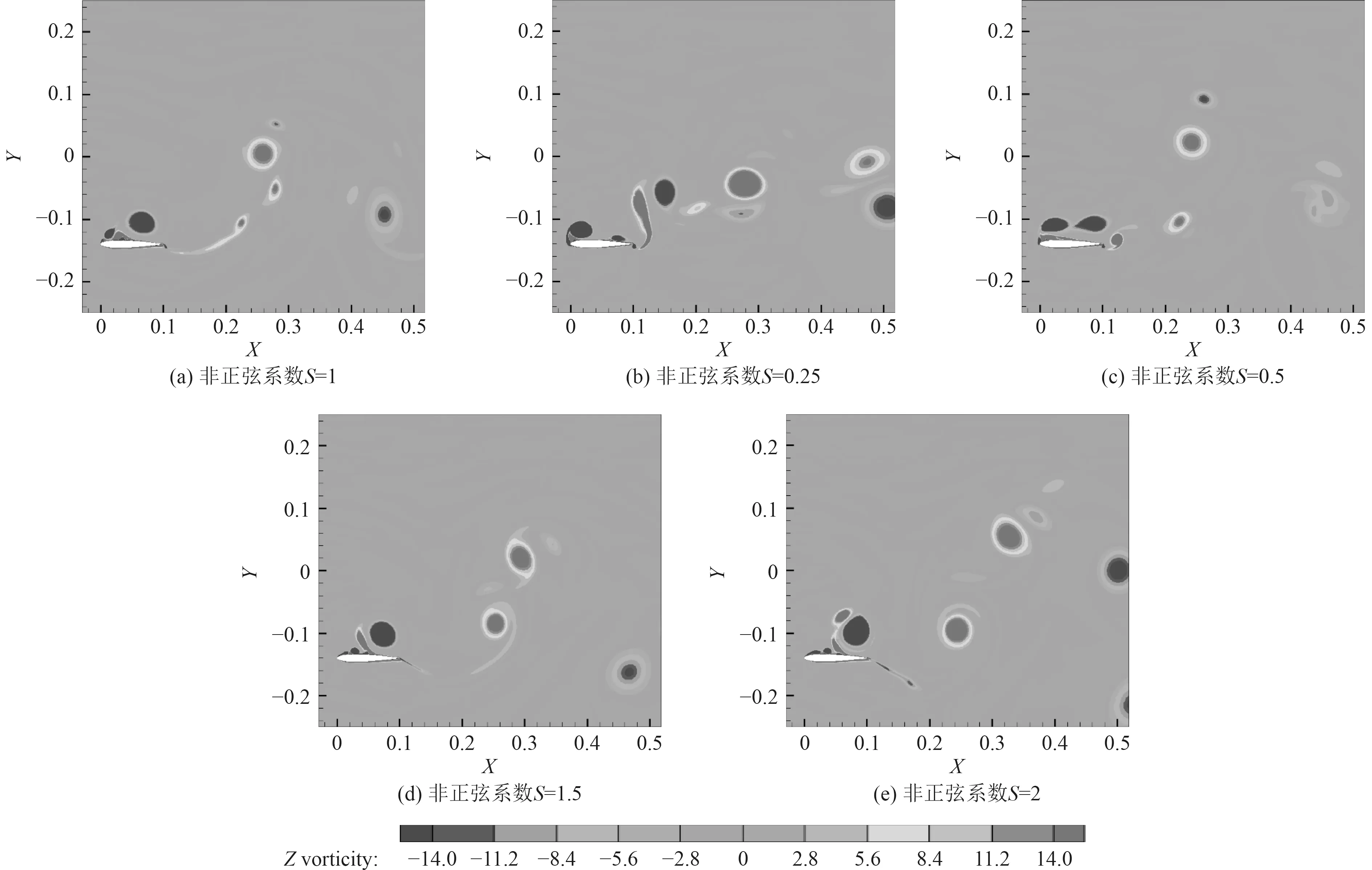
图10 前翼运动至最大负向位移位置处(t=0.5T)的涡量云图Fig. 10 The vorticity contour of the forefoil moving to the position of maximum negative displacement (t=0.5T)

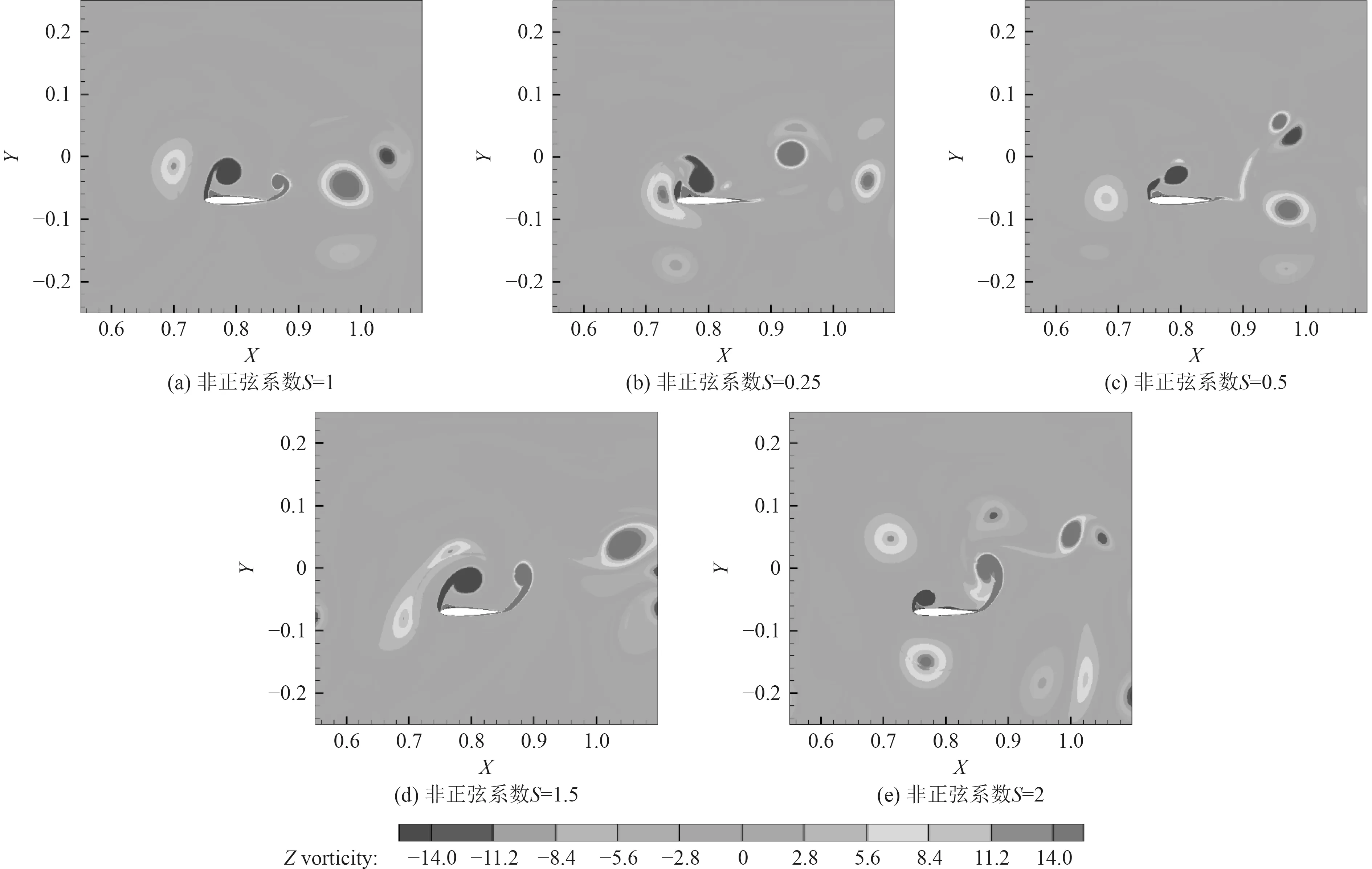
图11 后翼运动至平衡位置处（t=0.5T）的涡量云图Fig. 11 The vorticity contour of the hindfoil moving to the equilibrium position (t=0.5T)

对于后翼在非正弦系数=1时，有一个负向旋涡在首端脱落，有一个正向旋涡在尾端脱落。负向旋涡比正向旋涡强度更强，有一组旋向相反的涡在尾流中，观察到有前翼的尾涡运动到后翼附近。当＜1时，首端负向旋涡分为2个，尾端正向旋涡和尾涡中的负向旋涡随的减小而减弱。当＞1时，随着的增大，尾端的正向旋涡强度增强，首端负向旋涡强度减弱。

2.3 非正弦升沉系数S对推进表现的影响

从图12（a）可知，对于前翼，从非正弦系数=1增大或减少，均能增加前翼的平均推力系数。在=0.5时前翼平均推力系数在相位差为90°处变化明显，在此非正弦系数下，后翼对前翼的推力影响较大。从图12（b）可知：在大多数相位差下，从=1增大或减小非正弦系数可以增强后翼平均推力系数，但在某些相位差下，非正弦运动的平均推力系数小于正弦运动的平均推力系数。如相位差为0时，=0.5的平均推力系数小于=1的平均推力系数。总体来看，随着相位差的增加，平均推力系数先增后减。

从图12（c）可知，对于前翼的推进效率，当＞1时，推进效率随的增大而减小，当＜1，推进效率随的减小而增大。可以观察到在=0.5时，前翼推进效率曲线在不同的相位差下，数值发生较明显变化，推测是此非正弦系数和相位差时后翼对前翼的影响较大所致。从图12（d）可知，对于后翼的推进效率同样在＞1时，推进效率随的增大而减小，随相位差的增大先减后增，在＜1时，随的减小而增大，随相位差的增大先增后减。

图12 前后翼在不同相位差下，扑翼推进表现随非正弦系数的变化Fig. 12 Under different phase differences, the propulsion performance of the fore and hind foils changes with the non-sinusoidal coefficient

3 结 语

本文采用计算流体力学方法和重叠网格技术研究了非正弦运动对串列升沉水翼推进性能的影响，得到如下结论：

1）通过不同时间步长和网格尺寸的数值结果比较，验证了数值模型的收敛性；通过与公开发表试验和数值结果的比较，验证了数值模型的计算精度。

2）非正弦升沉运动相比于正弦升沉运动会增大扑翼的瞬时推力峰值和升力峰值，而且，非正弦系数的量值与1的偏差越大，瞬时峰值增大程度越明显。

3）非正弦系数可以改变水翼表面涡的脱落模式，当＜1时，一组尾涡由2个旋向相同、一个旋向相反的涡组成；当＞1时，一组尾涡由2对旋向相反的涡组成。

4）除个别少数相位差对应的运动状态，与正弦运动相比，当非正弦系数从=1增大或减小时，非正弦运动下的前翼和后翼平均推力增大。

5）除个别少数相位差对应的运动状态，与正弦运动相比，当非正弦系数从=1增大时，前翼和后翼的推进效率减小；当非正弦系数从=1减小时，前翼和后翼的推进效率增大。除此之外，在此基础上改变双翼相位差可以进一步使串列水翼达到最佳推进效率，这将为串列双翼水下航行器推进系统的设计提供指导。