多自由度下拖曳体迫沉水翼控制力特征研究
2022-10-18罗鹿鸣吴家鸣杨显原
罗鹿鸣,吴家鸣,杨显原
(华南理工大学 土木与交通学院, 广东 广州 510640)
0 引 言
水下拖曳体是一种在海洋研究、海洋监测等领域具有越来越广泛应用价值的水下探测平台,它依靠由水面工作母船通过拖曳缆绳而提供的拖曳力获得驱动其前进的动力,该类平台主要用于执行大范围水下搜索探测任务,根据不同搜索探测任务的功能需求,拖曳体可以搭载不同类型的水下化学、物理参数传感器。迫沉水翼作为水下拖曳体作业过程中升沉运动的主要控制机构,提高其在拖曳体操纵运动过程中,对迫沉水翼所发出的控制力进行准确有效的预测和模拟的水平,对性能优良的新型轨迹控制水下拖曳体研发设计具有重要的工程意义。
现阶段,包括滑移网格、动网格、重叠网格等技术已广泛运用于船舶与海洋工程装备与结构物的流场特性研究中。其中,重叠网格法是指将物体的每个部件单独划分网格,然后嵌入另一套网格之中,通过“挖洞”等预处理后,在剩余的网格重叠区域内建立插值关系,利用插值方法使网格间能传递流场数据信息。重叠网格法允许多个相互独立的网格之间产生无约束的相对运动,利用该技术能很好地处理物体在流场中的多自由度运动问题。在船舶工程数值模拟计算中,重叠网格法能够实现在船体自身运动的基础上叠加螺旋桨以及舵的旋转运动,并可以获取它们之间相互作用的流场信息,是实现船、桨、舵配合以及自航操纵计算研究比较有效的数值方法之一。本文采用重叠网格技术,运用相对运动原理模拟不同拖速下,迫沉襟翼在一定偏转角幅值范围内进行正弦摆动运动时的拖曳体及迫沉水翼的水动力特征。
1 数学模型及计算方法
1.1 控制方程与湍流模型
假定计算中流体为不可压缩粘性流体,密度为常数,则其质量守恒方程为:
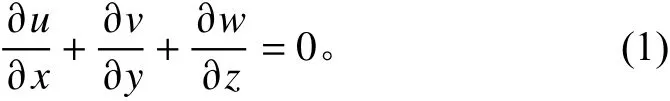
动量守恒方程为:

式中:τ,τ和τ为微元体表面上黏性应力τ的分量;F ,F 和F为微元体上的体积力,若该体积力只有重力,且轴竖直向上,则F=0,F=0,F=ρ。
选用隐式不定常、-ω湍流、分离流,湍动能方程如下:

Omega方程:

式中:

辅助关系式:

1.2 水下拖曳体几何模型的构建以及坐标系
本文所研究的拖曳体为一多自由度可控制水下拖曳体,其主体为立式长流线型结构,2个对称的鱼雷形浮筒分布在主体左右,两浮筒之间以固定水平翼相连。固定水平翼尾部设置了可操纵转角迫沉襟翼,两者一起构成了迫沉水翼。实际操作中通过改变迫沉襟翼转角,诱导固定水平翼攻角变化,进而获得使拖曳体上下升沉运动的控制力,以此来实现对拖曳体的深度控制。两浮筒尾部还设置有用于对拖曳体在水平面运动时转首姿态控制的导管螺旋桨。
由于本文以分析作为拖曳体在垂直面上升沉运动的主要控制机构迫沉襟翼进行正弦摆动运动时的水动力特性为主题,构建拖曳体几何模型时,对导管螺旋桨的几何特征做了简化处理。基于这些考虑所构建的水下拖曳体几何模型如图1所示,其基本几何尺寸见表1。
本文计算所采用固定坐标系统如图2所示。
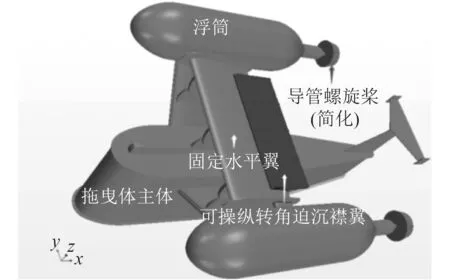
图1 水下拖曳体模型Fig. 1 Underwater towed body model
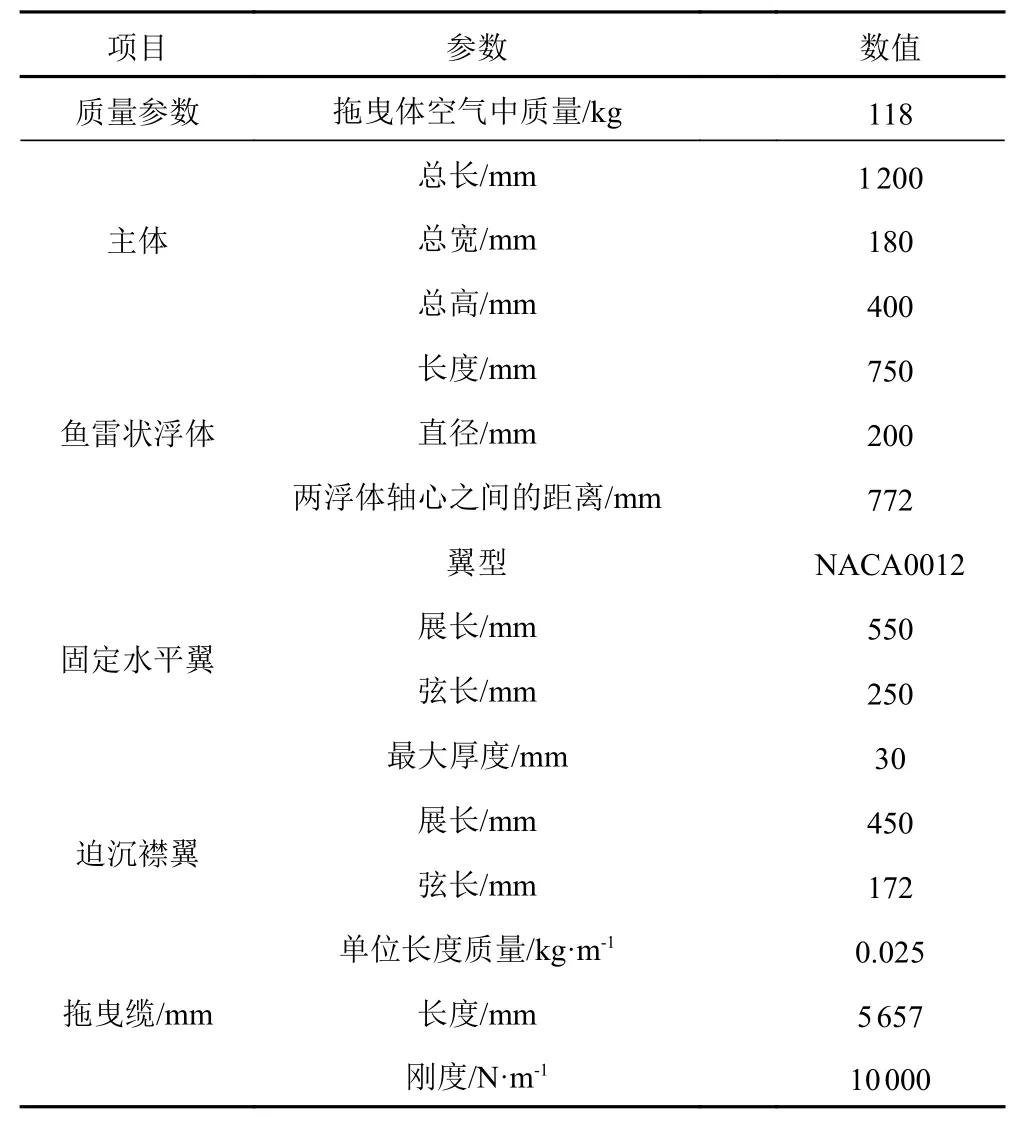
表1 水下拖曳体系统基本几何参数Tab. 1 Basic geometric parameters of underwater towed body system
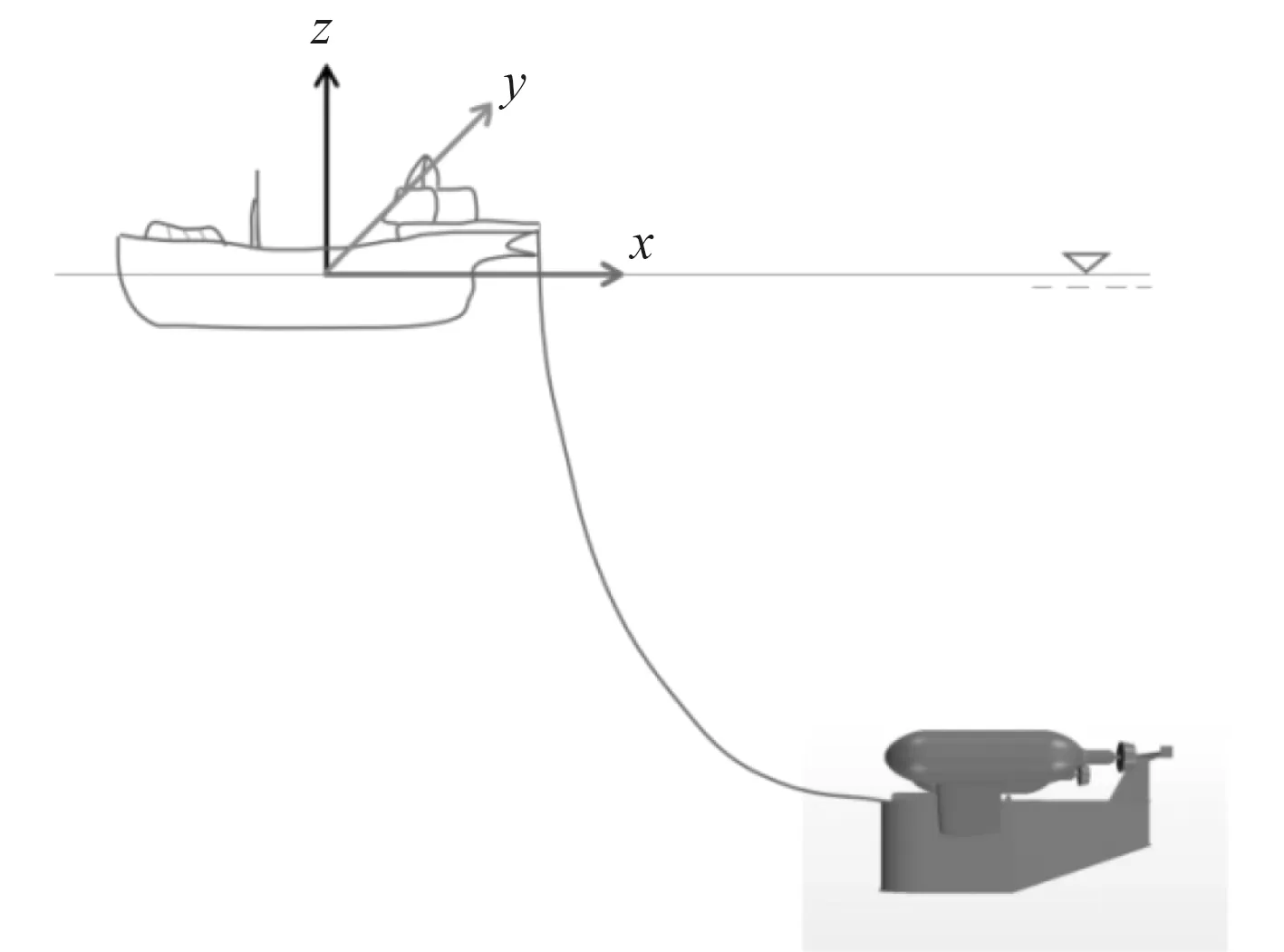
图2 本计算所采用的固定坐标系统Fig. 2 The fixed coordinate system used in this calculation
1.3 单独迫沉襟翼的运动方式
作为拖曳体升沉运动控制机构,本文所研究的迫沉襟翼转角 Φ ()绕摆动轴以正弦规律摆动。

式中:为时间,s ; Φ ()为转角,(°)。式(7)表明,迫沉襟翼转角以=20s为一个周期进行正弦摆动。则迫沉襟翼摆动的角速度为

式中:ω为角速度,s。
1.4 计算域网格的划分
采用STAR-CCM+ 对拖曳体在拖曳过程中,其迫沉襟翼进行正弦摆动运动时的水动力特征进行分析。
首先需要构建1个长×宽×高=12 000 mm×10 000 mm×8 000 mm的长方形计算域,作为整体计算的背景域,拖曳体位于该计算域纵向轴的中心,拖曳体最前端离计算域进口的距离为5 000 mm,以保证拖曳体去流段维持一定的长度,避免尾流对计算结果的影响。采用运动相对性原理,以计算域的进流速度取代拖曳体的拖速,通过这样一种方式来观察拖曳体在特定拖速下的水动力特性。图3为所构建的长方形计算域,以及拖曳体在域中的相对位置。图中,轴正方向为来流方向,轴方向为摆动轴方向,轴正方向为竖直向上方向。
为了研究迫沉襟翼在沿拖曳方向(轴负方向)上在不同拖速下控制力特征,需要创建一个以其摆动轴为轴,包含迫沉襟翼的半径为210 mm的圆柱体区域(即图4中的Cylinder区域)。对圆柱体Cylinder与迫沉襟翼做布尔运算(目标为保留Cylinder)得到圆柱形旋转计算域Ⅰ。同时,为了观察拖曳体的多自由度运动,创建一个如图5所示的长×宽×高=1 700mm×1 200mm×1 100 mm包裹着拖曳体的小立方体区域。对小立方体与拖曳体主体做布尔运算(目标为保留小立方体),得到小立方体计算域Ⅱ;将零部件“长方形计算域”分配给区域,得到背景计算域Ⅲ。
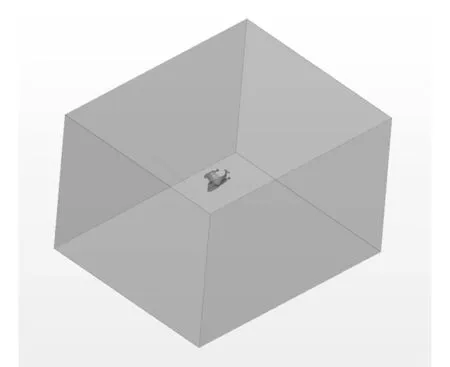
图3 长方形计算域Fig. 3 Rectangular computational domain
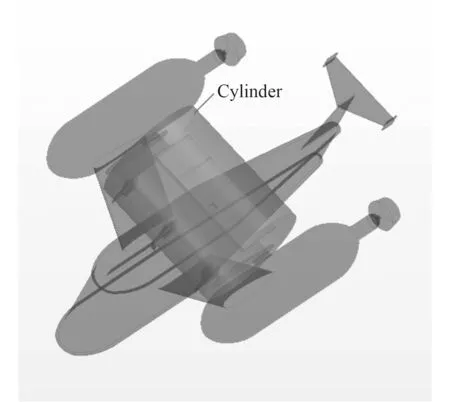
图4 Cylinder Fig. 4 Cylinder
所有计算域划分效果如图5所示。

图5 计算域Fig. 5 Computational domain
为实现不同计算域之间的流场信息交换,需要对计算域Ⅰ和Ⅱ创建重叠网格1交界面,对计算域Ⅱ和Ⅲ创建重叠网格2交界面。同时为更好地优化建立计算域Ⅰ和Ⅱ边界之间的联系,新建一个与Cylinder同轴、半径为220 mm的圆柱体Cylinder加密(见图6),并对小立方体网格添加目标零部件为“Cylinder加密”的体积控制节点。

图6 Cylinder加密Fig. 6 Cylinder encryption
为更好优化建立计算域Ⅱ和Ⅲ边界之间的联系,还需新建1个长×宽×高=4 0 0 0 m m×2 0 0 0 m m×7 000 mm包裹着计算域Ⅱ的立方体“水池加密”(见图7),并对背景计算域网格Ⅲ添加目标零部件为“水池加密”的体积控制节点,其相对尺寸与小立方体网格2中小立方体表面网格尺寸一致,这保证了两者网格重叠区域使用相同的方格密度数量级,最大程度上消除在2个网格间插入变量时产生的错误。
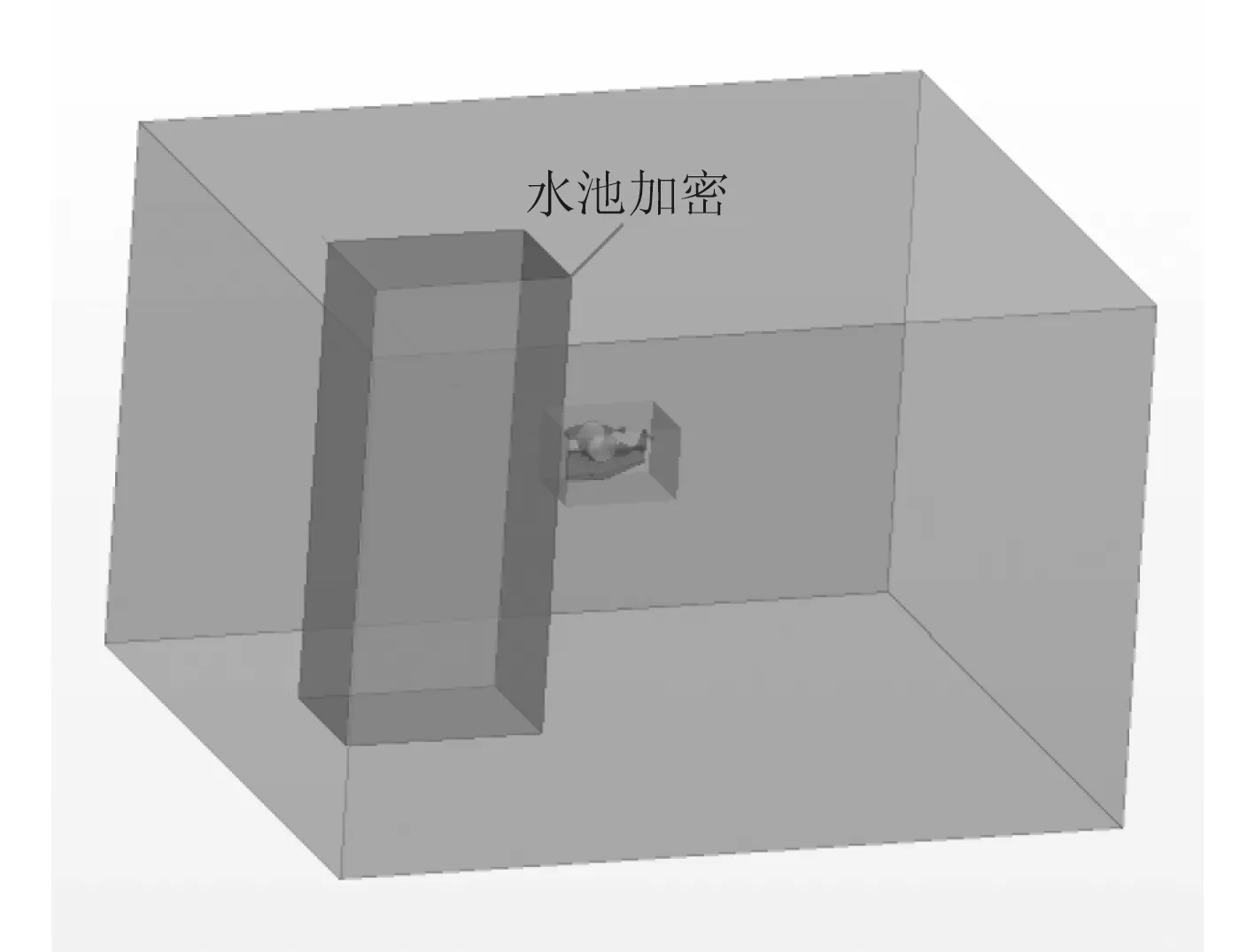
图7 水池加密Fig. 7 Pool encryption
由于在拖曳体斜上方设置了一条拖曳缆,为了更好地研究拖曳体在拖曳缆作用下的运动特性,围绕斜上方拖曳点新建2个半径分别为6.5 m,4.5 m,厚度为2 m的圆柱体Cylinder2,Cylinder3,针对2个圆柱体做布尔运算得到一个闭合圆环(见图8),对背景计算域Ⅲ添加目标零部件为“闭合圆环”的体积控制节点,显然拖曳体主要在水池与闭合圆环的重叠圆弧段运动。
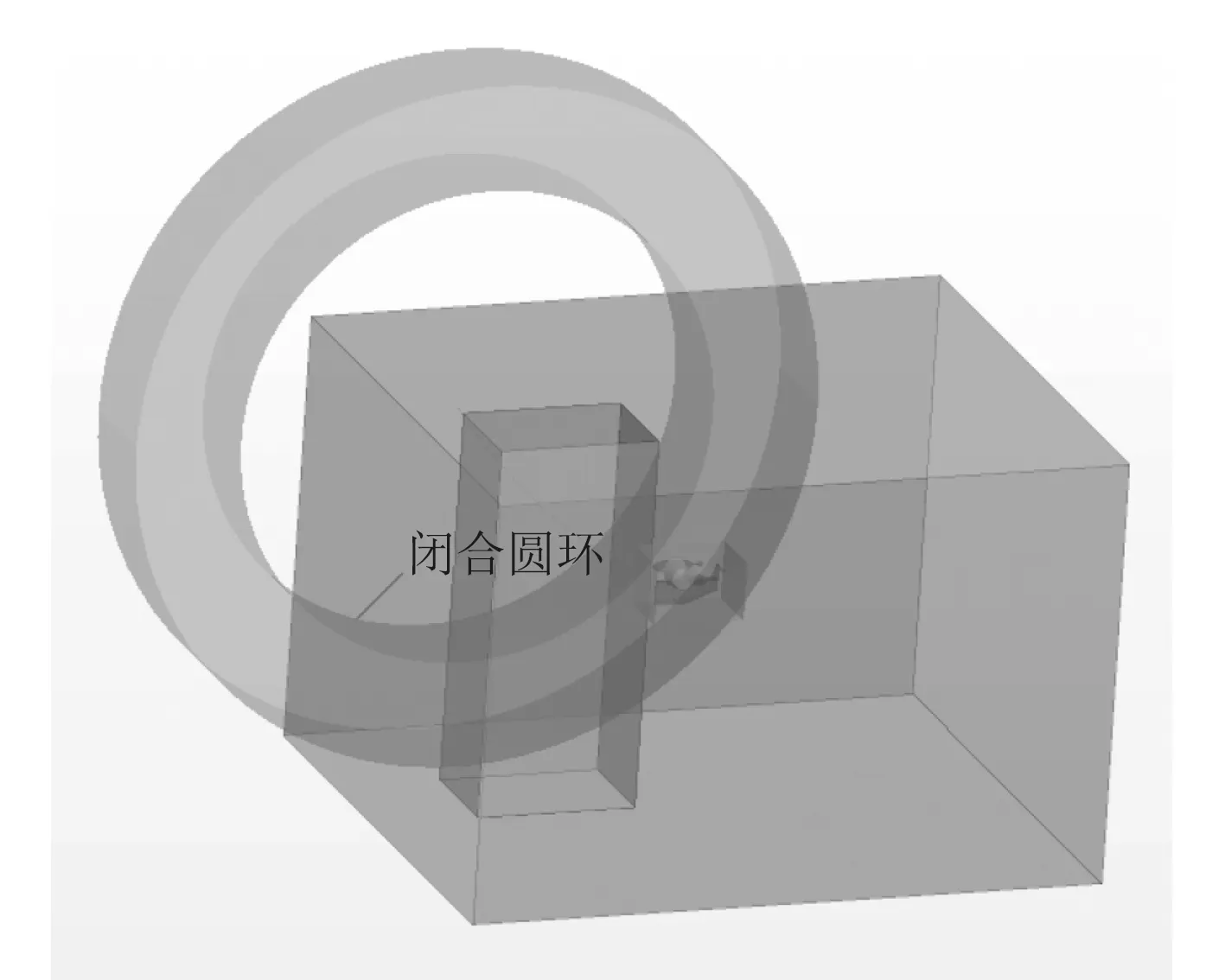
图8 闭合圆环Fig. 8 Closed circle
最后针对3个计算域创建3种不同质量的网格操作,圆柱形旋转计算域Ⅰ采用较为精细的网格1,小立方体计算域Ⅱ采用密度适中的网格2,背景计算域Ⅲ则采用较稀疏的网格3,它们的基准值参见表2。

表2 网格操作控制基准值Tab. 2 Grid operation control reference value
1.5 设置DFBI和六自由度求解器
在STAR CCM+中,设置DFBI(dynamic fluid body interaction)运动可实现对模型六自由度运动的模拟,该方法尤其适用于模拟刚体在流体作用下的被动作用。在本文的模型中,只有迫沉襟翼主动摆动,而拖曳体主体与固定水平翼则在流场作用下被动运动。为了研究迫沉襟翼的摆动是如何影响拖曳体的升沉运动,以及考虑拖曳体的结构因素对迫沉襟翼水动力特性的特殊影响,并更好地在拖曳体系统中观察固定水平翼及迫沉襟翼的水动力特性,本文采用六自由度求解器并以拖曳体主体与迫沉水翼为目标零部件,设置“DFBI旋转和平移”运动方式,同时将小立方体计算域Ⅱ的运动规范设置为“DFBI旋转和平移”;对新建的多自由度体拖曳体建立体驱动运动“拖曳体-Motion”,并叠加旋转运动,旋转轴沿轴方向,旋转速率依照式(8),同时将圆柱形旋转计算域Ⅰ的运动规范设置为“拖曳体-Motion”。
1.6 边界条件的设置
表3给出了各计算域之间的边界条件类型。

表3 边界条件的设置Tab. 3 Setting of boundary conditions
2 数值模拟及计算结果分析
根据所要研究对象的计算性质和重叠网格技术的要求,采用以上所构建的计算域对拖曳体在一定拖速范围内,迫沉襟翼以一定的幅角正弦摆动下所表现出的水动力特性进行计算,观察在这样的拖曳工况下:1)迫沉襟翼在转角摆动过程中所产生的迫沉力、所受到的阻尼力以及相应的力矩变化规律;2)固定水平翼和拖曳体主体在迫沉襟翼转角摆动所产生的摆动力矩作用下的水动力学特征;3)迫沉襟翼、固定水平翼和拖曳体主体三者的动力学特征关系。
2.1 迫沉襟翼、固定水平翼和拖曳体主体在拖曳作业中的水动力特征
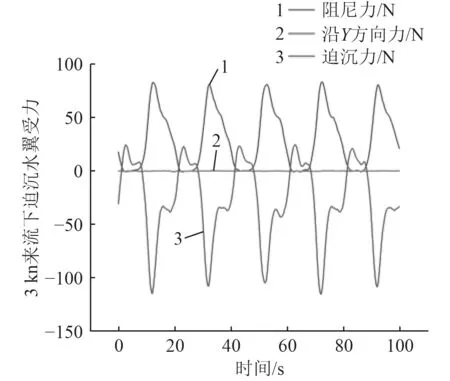
图9 3 kn拖曳速度下迫沉襟翼受力Fig. 9 The force on the flaps forced at the towing speed of 3 kn
图9给出了在拖曳速度为3 kn、迫沉襟翼的转角以方程(7)所规定的正弦规律摆动下迫沉襟翼所产生的诱导迫沉力、所受到的阻尼力;图10给出了在迫沉襟翼所产生的诱导迫沉力驱动下,固定水平翼所产生相应的迫沉力和阻尼力;图11给出了在这样的迫沉襟翼摆动下,迫沉襟翼和固定水平翼所产生的纵倾力矩。而图12和图13则给出了这些力矩的作用下,拖曳体整体的纵倾角时间历程及其相对于拖曳缆上端拖曳点的纵荡与垂荡运动时间历程。

图10 3 kn拖曳速度下固定水平翼受力Fig. 10 The force on the fixed horizontal wing at the towing speed of 3 kn

图11 3 kn拖曳速度下迫沉襟翼和固定水平翼所受力矩Fig. 11 Torques to force down flaps and fixed horizontal wings at the drag speed of 3 kn
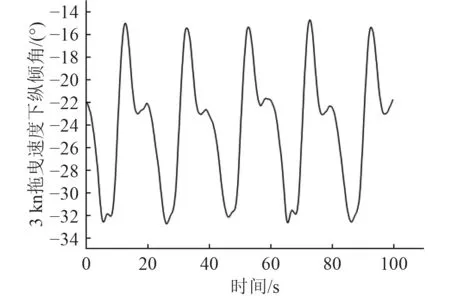
图12 3 kn拖曳速度下拖曳体纵倾角Fig. 12 Inclination Angle of towed body at towing speed of 3 kn
对图9~图13的计算结果进行分析,可以看出迫沉襟翼、固定水平翼和拖曳体之间存在着如下的一些动力学关系:
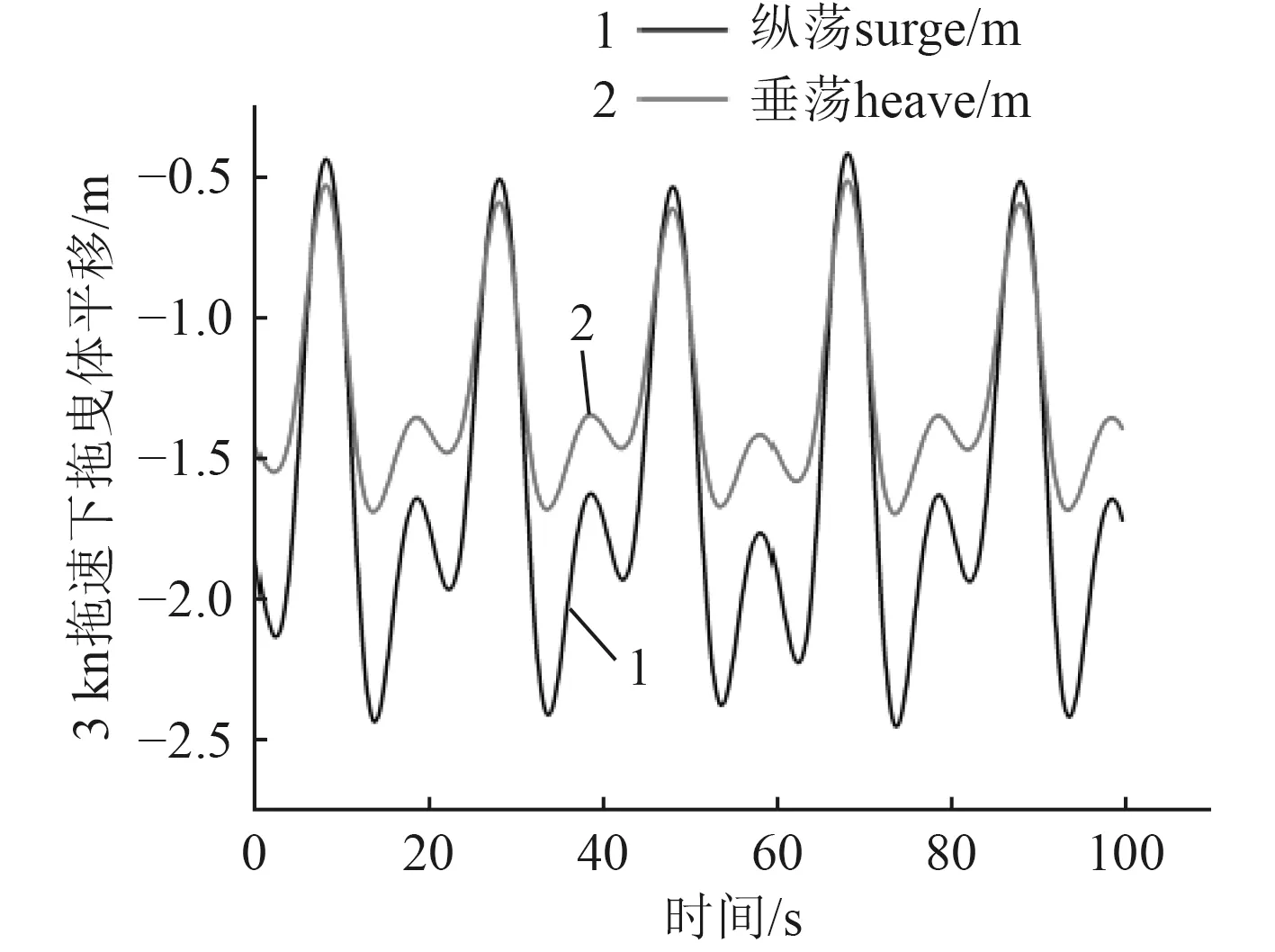
图13 3 kn拖曳速度下拖曳体体平移Fig. 13 The towed body shifts at the towed speed of 3 kn
1)迫沉襟翼、固定水平翼和拖曳体的力学与运动变化模态相同,它们的变化周期与迫沉襟翼转角摆动周期一致。从图8~图13的计算结果可以看到,迫沉襟翼、固定水平翼升力、阻尼力以及它们所产生相应力矩的振荡周期,拖曳体整体纵倾角、纵荡与垂荡运动时间历程的变化周期均为20 s。这一周期与方程(7)所设定的迫沉襟翼摆动周期一致。
2)在本文所研究的拖曳体垂荡及纵倾角摆动控制中,首先控制迫沉襟翼转角的改变使之对拖曳体产生一个纵倾力矩,以此诱导固定水平翼攻角的改变,依靠固定水平翼偏转所提供的较大迫沉升力和纵倾力矩来操纵拖曳体垂荡运动,从而实现对其深度控制。从图9~图11的计算结果可以看出,固定水平翼产生的迫沉升力约为迫沉襟翼所产生的迫沉升力的1倍;固定水平翼所产生的纵倾力矩约为迫沉襟翼所产生的纵倾力矩的3倍。而在这样的垂荡运动操纵过程中,两者所受阻尼力的大小基本相同。图9~图11的计算结果表明,通过这样一种以操纵迫沉襟翼转角来诱导固定水平翼水动力攻角改变的控制方式,可以用比较小的驱动转矩来实施对拖曳体的垂荡运动操纵,这种操纵方式可以降低拖曳体深度控制机构的设计难度。
3) 显然,对于本文所研究的拖曳体,由于其整体结构及操纵方式均沿纵剖面对称,在目前的这一控制运动状态下,拖曳体所受的沿Y轴方向的侧向力为0。
2.2 迫沉襟翼与固定水平翼之间的动力学关系分析
图14为拖曳速度在1.5~4.0 kn范围内迫沉襟翼产生的诱导迫沉力、所受到的阻尼力的最大幅值;图15为在这样的拖曳速度范围内,由迫沉襟翼所产生的诱导迫沉力驱动下,固定水平翼所产生相应的迫沉力和阻尼力最大幅值;图16为迫沉水翼与固定水平翼2种翼型升阻比系数随拖速变化图;图17为相应的迫沉襟翼和固定水平翼所产生的纵倾力矩最大幅值。
对图14~图17的计算结果进行观察,可以发现迫沉襟翼和固定水平翼之间的迫沉力与阻尼力分量有如下动力学关系:

图14 迫沉襟翼受力峰值随拖速变化图Fig. 14 Diagram of force peak value of forced flaps varying with towing speed
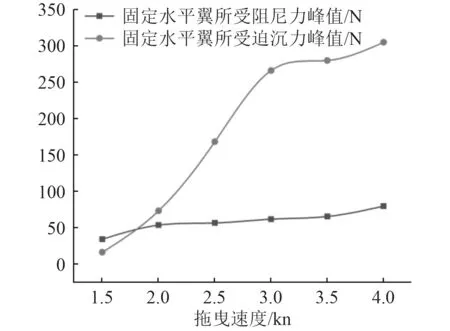
图15 固定水平翼受力峰值随拖速变化图Fig. 15 Diagram of variation of force peak of fixed horizontal wing with towing speed

图16 翼型升阻比随拖速变化图Fig. 16 Diagram of airfoil lift-drag ratio varying with towing speed
1)在所计算的拖速范围内,迫沉襟翼所产生的迫沉力小于它所受的阻尼力,其升阻比随拖速变化较小且均小于1。
2) 固定水平翼的迫沉力最大幅值随拖速的增大而显著增大,而所受的阻尼力幅值随拖速增大的幅度不明显,其升阻比在大部分拖速范围内均大于1,升阻比在一定拖速范围内随拖速的增大而逐渐增大。
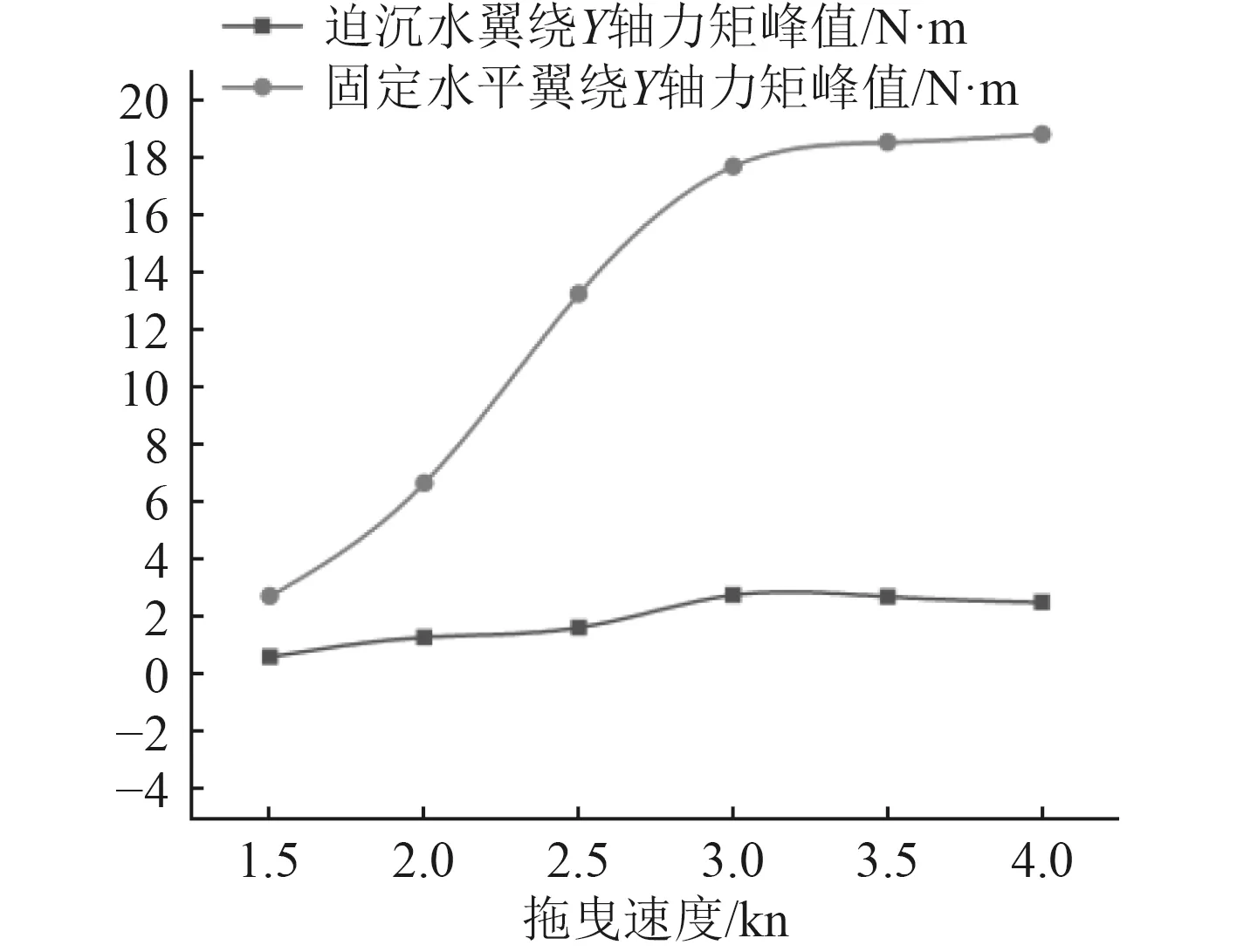
图17 迫沉襟翼和固定水平翼绕Y轴力矩峰值随拖速变化图Fig. 17 Diagram of the change of the Y-axis moment peak value with towing speed of the forced flaps and fixed horizontal wings
3)在所计算的拖速范围内,迫沉襟翼和固定水平翼所受到的阻尼力其量值大致相当。但是,固定水平翼所产生的迫沉力以及由此而产生的纵倾力矩幅值则远远大于迫沉襟翼的相应值。在4 kn的拖速条件下,固定水平翼的迫沉力与纵倾力矩分别为迫沉襟翼的4倍和7.5倍。
对上述动力学关系计算结果的观察说明:采用本文所研究的拖曳体深度操纵方式,对拖曳体深度操纵产生控制力其实主要来自于固定水平翼,而迫沉襟翼所起的作用则在于诱导固定水平翼水动力攻角改变,进而使固定水平翼产生足够大的迫沉力,从而达到提高拖曳体深度操纵效率的目的。
2.3 拖曳体整体动力学关系特性分析
图18~图21给出了在拖曳体整体在迫沉襟翼转角摆动所产生的摆动力矩作用下,拖曳体拖曳体平均深度、平均纵倾角、与拖点的水平和垂直距离与拖曳速度的关系。从这些结果中可以看出,随着拖曳速度的增大,拖曳体的平均纵倾角减小,平均深度增大,平均水平距离减少。
为了分析图18~图21的原因,对特定拖曳速度下作用于拖曳体整体的水动力载荷、拖曳体的重力与浮力以及拖缆张力,在固定坐标系中分别按水平与垂直方向进行分解(见图22),其结果由表4给出。可知,产生所观察到的这些现象其原因在于:在这些拖曳工况中,拖曳体整体所受到的水动力(包括在水下所受到的浮力),其垂直分量为垂直向上的升力,当拖曳速度增大时,拖曳体的平均纵倾角在减小,它所受到的垂直向上的升力也在降低。由于拖曳体本身的自重不会随着拖曳工况的变化而改变,相应地,拖曳体整体受竖直方向的迫沉力(水动力与重力的差值)在增大,从而驱动拖曳体往更大的深度迫沉。

图18 拖曳体平均纵倾角随拖速变化图Fig. 18 Diagram of average longitudinal Angle of towed body changing with towing speed
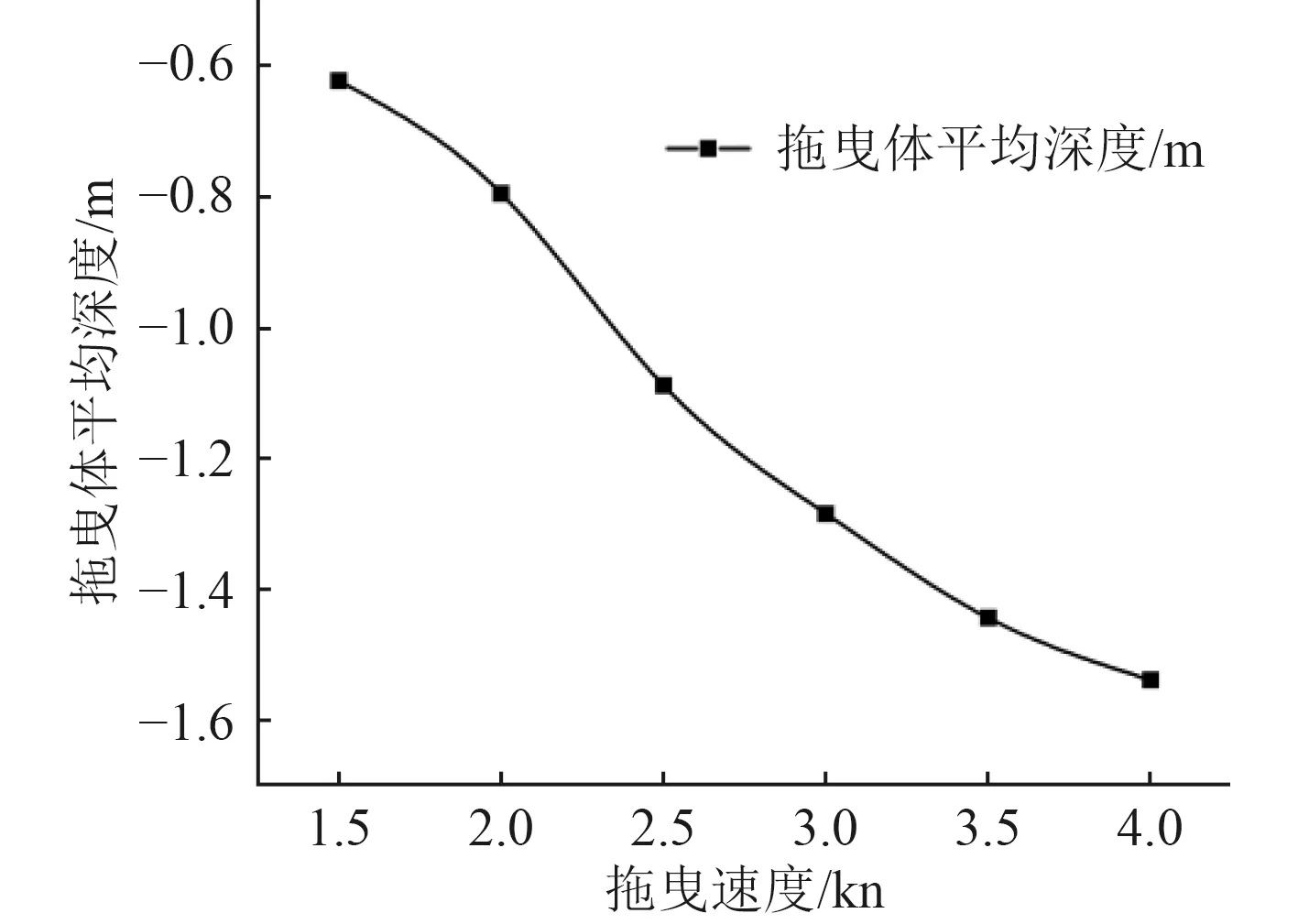
图19 拖曳体平均深度随拖速变化图Fig. 19 Average depth of towed body varies with towing speed
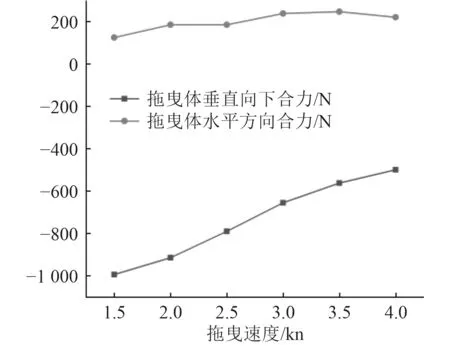
图20 拖曳体合力随拖速变化图Fig. 20 Diagram of resultant force of towed body changing with towing speed
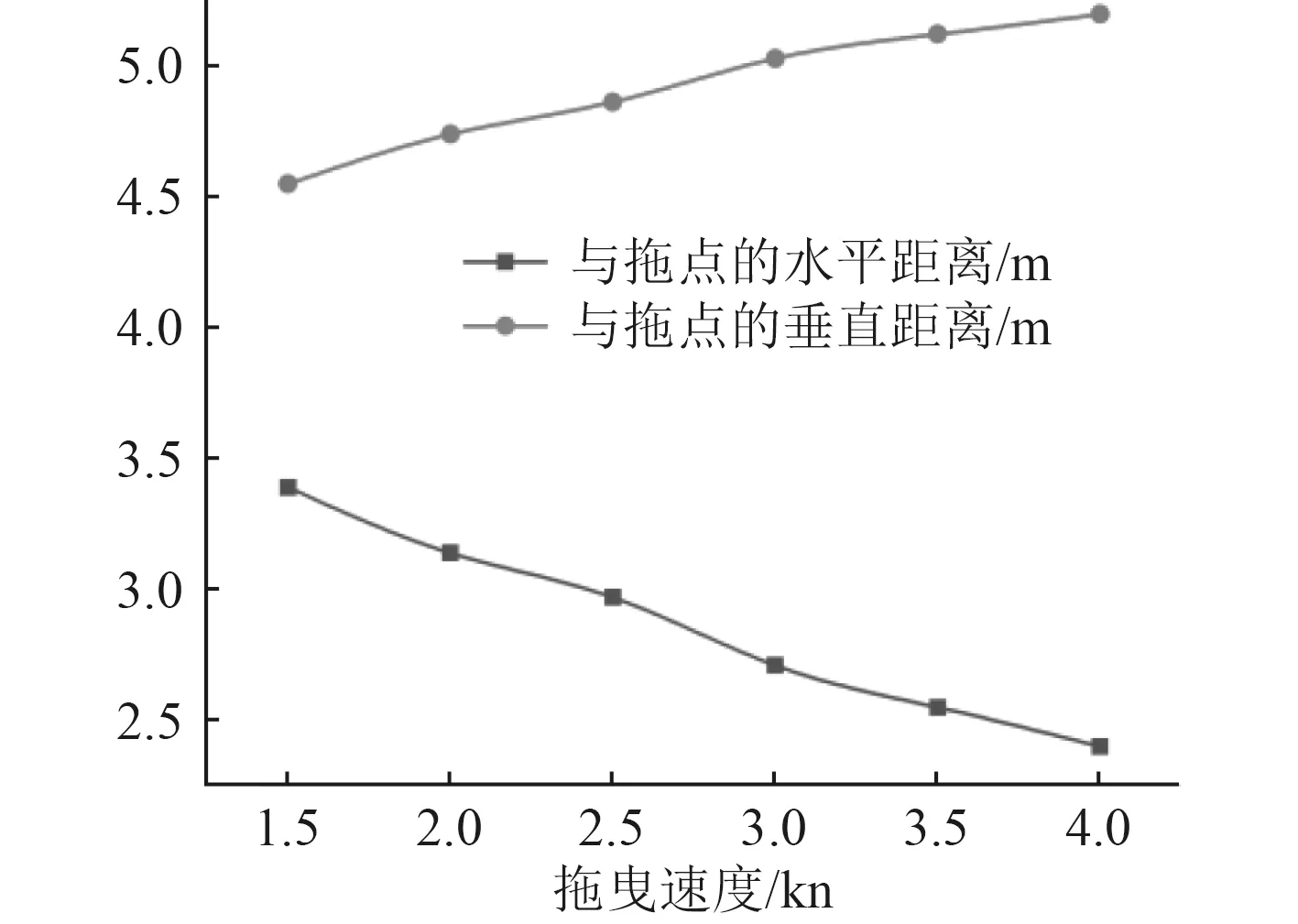
图21 拖曳体与拖点距离随拖速变化图Fig. 21 Diagram of distance between towed body and towed point changing with towing speed
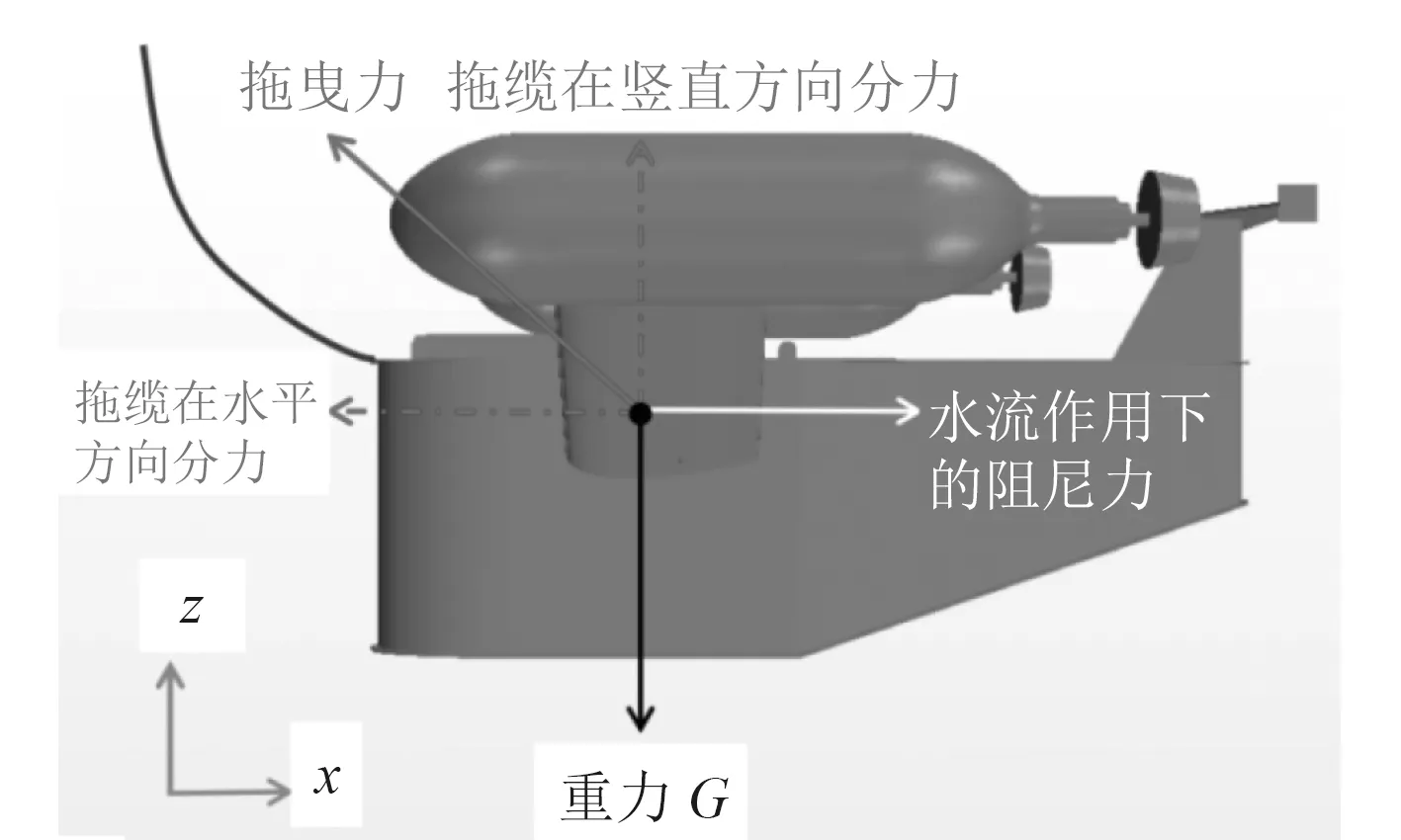
图22 拖曳体受力分析图Fig. 22 Force analysis diagram of towed body
拖曳体在所讨论的拖曳工况中,拖曳体所受到的由拖曳体在水下运动中所受到的水动力载荷、拖曳体本身的重力与浮力以及拖缆张力所构成的力系达到了一种力学平衡状态。从表4的计算结果可以看出,对于不同的拖曳速度,拖曳体在固定坐标系下的水平与垂直方向各种分量的合力大致为0。

表4 拖曳体水平与垂直方向受力分量对比Tab. 4 Comparison between horizontal and vertical force components of towed body
3 结 语
本文采用CFD软件STAR-CCM+,运用重叠网格技术对迫沉襟翼在1.5~4.0 kn范围内进行正弦摆动运动下,迫沉襟翼产生的诱导迫沉力、所受到的阻尼力;由迫沉襟翼所产生的诱导迫沉力驱动下,固定水平翼所产生相应的迫沉力和阻尼力;拖曳体在这样的拖曳工况下所受到的水动力载荷,所表现的运动特征进行数值模拟。对本文的计算结果进行分析,可以发现拖曳体各组成部分有如下动力学特征:
1)拖曳体各组成部分(迫沉襟翼、固定水平翼、拖曳体整体)的动力学振荡周期实际上是由迫沉襟翼的摆动周期所诱导,它们的变化周期均与迫沉襟翼摆动周期一致。
2)本文所研究的拖曳体的控制方式是,首先控制迫沉襟翼转角的改变使之对拖曳体产生一个纵倾力矩,以此诱导固定水平翼攻角的改变,依靠固定水平翼偏转所提供的较大迫沉升力和纵倾力矩来操纵拖曳体的升沉运动,从而实现对其深度控制。这一控制方式的优势是可以用比较小的驱动转矩来实施对拖曳体的升沉运动操纵,从而降低拖曳体深度控制机构的设计难度。
3)拖曳体在其水下拖曳作业过程中所受到的水动力载荷、拖缆对其所施加的张力,以及拖曳体本身的重力与浮力构成了一种力学平衡状态,拖曳体所受到的合力在整个作业过程中一般都大致为0。
