基于量子粒子群算法的船舶机舱布局方法
2022-10-18黄金娥黄祥兵闵少松
崔 奥,黄金娥,黄祥兵,江 杰,闵少松
(1. 海军工程大学 舰船与海洋学院,湖北 武汉 430033;2. 中国人民解放军92942部队,北京 100161)
0 引 言
目前,大多数的布局算法都是启发式与元启发式相结合的方法。其中,启发式算法的求解思路主要是根据问题特点,缩小搜索空间,进而得到最终解。这种算法虽能保证解的质量,但是通用性不强。元启发式方法则是运用遗传算法、粒子群算法等计算机智能优化算法,用随机的方式搜索邻域或者将多个解综合成新解。这种算法通用性强,但是其结果受智能算法收敛性的影响较大,经常性出现结果不稳定的情况。因此,在布局优化中,2种方法经常被混合使用,以提高算法性能。
船舶机舱布局设计作为布局问题的一种,在满足一般性布局问题要求的同时,还需要根据舱室环境的特殊性,结合船舶设计规范以及舱室设备布置要求,进行额外的约束,并在求解过程中,将各类约束转化为罚函数的形式加入到目标函数中,进而利用计算机智能算法进行求解。但是求解思路主要集中在对算法的改进与优化上,未能对启发式算法的优势进行充分利用。此外,针对粒子群算法早收敛的特点,Sun J等提出了量子粒子群算法,并在各个领域作为粒子群算法的改进算法得到了广泛应用,但是尚未应用于船舶舱室的布局问题。
本文借鉴启发式布局的方式进行初始解的生成,运用量子粒子群算法对某型船舶机舱的设备进行布置,并与遗传算法和粒子群算法进行对比,说明本文给出的基于量子粒子群算法的布局方法具备更佳的算法性能。
1 问题描述与模型建立
1.1 问题描述与模型的简化
机舱布局优化问题分为三维布局与二维布局,本文主要在二维层面进行考虑,旨在求得机舱设备摆放位置的集合,使得船舶的机舱布局最为合理。可以表示为:={(,,),···,(x,y,α)},其中(x,y)为设备的形心坐标,α为设备摆放的方向,为设备的数量。
为了合理表述这个复杂的问题,并建立相应的模型求解,本文进行以下简化和假设:
1)在舱室布置时,主要考虑对舱室布局有较大影响的设施,管路、电缆以及壁挂式部件不做考虑。
2)将具有复杂形状的设备简化为规则的长方体。
3)通过垂直投影将三维布局问题简化为以舱室甲板为平面的二维布局问题。
4)舱室内部一些大型设备在设计初期已经固定,如柴油机等。
5)舱室入口和可拆板以及吊装通道的位置已经确定。
6)对不同设备、维修和操作位置可能会有所不同,但是每个设备的维修和操作位置相对为设备本身而言是固定的。
7)设备的摆放朝向问题仅考虑设备的长边与船舶长度方向平行和垂直的2种情况,即α={0,1}。
1.2 数学模型的建立
一般情况下,船舶舱设备布置需考虑船舶舱室的设计规范及设备布置需求,因此该问题是一个带复杂约束的多目标优化问题,可建立方程如下:
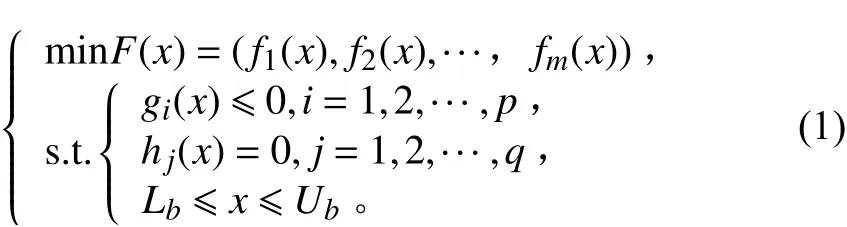
式中:为设计变量,包括设备的位置坐标及方向等参数,g()和h()分别为设备之间的功能性约束与几何约束转化的不等式约束与等式约束,为不等式约束个数,为等式约束个数,L和U则为设备布局的边界。
1.3 目标函数
本文主要从满足舱室设备基本布局的基础上,便于设备维修保养的角度出发建立目标函数。主要从不平衡力矩、维修干涉、船员流通距离以及吊装距离等方面进行舱室设备的布置。
1)不平衡力矩最小
相对于纵倾而言,船舶的横倾对船舶的设计以及使用影响更大,因此本文主要考虑横倾,尽量保证设备对船舶中纵剖面力矩的代数和最小。可定义不平衡力矩函数为:
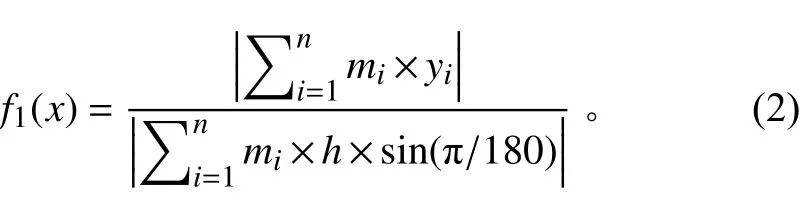
式中:为设备数量,m为设备的质量,y为设备形心到中纵剖面的距离,为船舶的初稳性高。
2)维修干涉最小

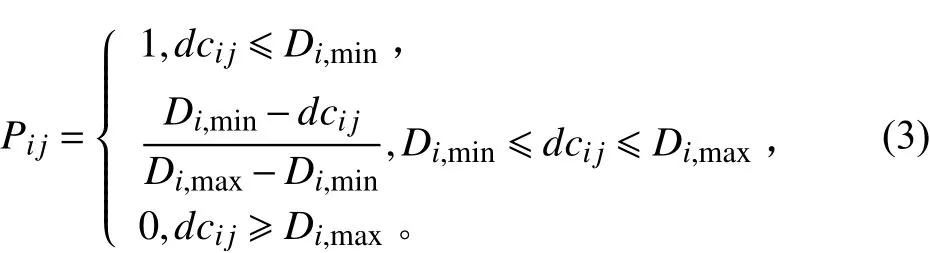
式中:D为设备的最小维修距离要求,D为设备的最大距离需求,dc为设备与的距离。在考虑维修干涉的过程中,还应该考虑设备的作业频率f,因此定义船舶舱室设备维修干涉的目标函数为:
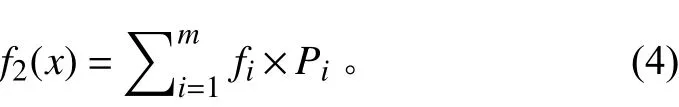
3)人员流通距离最小
良好的设备布局应当满足舱室人员快速出舱的需求,以便在紧急情况下船员能够迅速撤出工作舱室。定义船员的流通距离函数为:
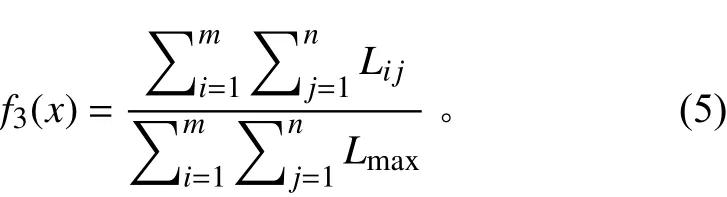
式中:L为设备到出口的距离,为舱室除舱口外的设备数量,为舱口数量,为舱室的对角线长度。
4)吊装距离最小
在对船舶舱室设备进行维修的过程中,需要将部分设备吊装出舱外进行维修,因此需要考虑设备的吊装距离。可定义吊装函数为:

式中:为需要吊装设备数量;T为设备到吊装出口的距离,T= |x-x|+|y-y|;T为设备在舱室中的顶角布置时,到吊装口的距离。
1.4 约束条件
1)设备之间不干涉


式中:l为设备的长,h为设备的宽。
2)设备在舱室内
在设备布置的过程中,设备应当全部在舱室区域以内,即()={A⊂}。
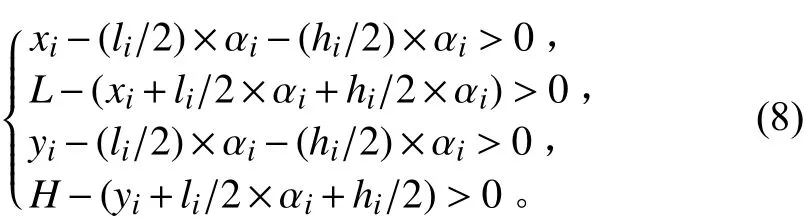
式中:为舱室长,为舱室宽,α为设备的方向。
3)其他约束
在布置过程中,还需要考虑设备的距离要求以及布置区域等其他类因素,记为:
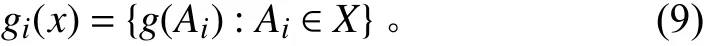
式中,为布局过程中的其他约束要求。则最后的适应度函数可定义为:

式中:f为目标函数;ω为目标函数的权重,本文取ω=0.2;为违反约束条件的惩罚值。
2 基于量子粒子群算法的布局优化
2.1 遗传算法和粒子群算法
遗传算法(GA)是一种基于种群的启发式算法,是当前最流行的进化算法之一。该算法是一种全局收敛性的算法,它通过遗传、变异的方式实现种群内部的信息交换,使拥有较高适应度的染色体得以保留,通过多次迭代进化,进而得到最优解。
粒子群算法(PSO)是一种基于群体智能的进化计算方法,具有较强的局部搜索能力。该算法受到鸟类觅食行为的启发,将种群中的每个粒子均视当前的候选解,在迭代过程中,通过种群中的粒子在多维空间搜索过程中的竞争和合作,进而寻找最优解。
2.2 量子粒子群算法
粒子群算法虽然有较强的局部搜索能力和一定的全局搜索能力,但是其本身存在一定的局限性,并且已经被学者Van den Bergh证明,该算法不是一个全局收敛的算法。对此Sun等在粒子群算法的基础上,将PSO算法公式进行改进,提出了量子粒子群优化算法(QPSO),并对其全局收敛的性质进行证明,其算法公式如下:
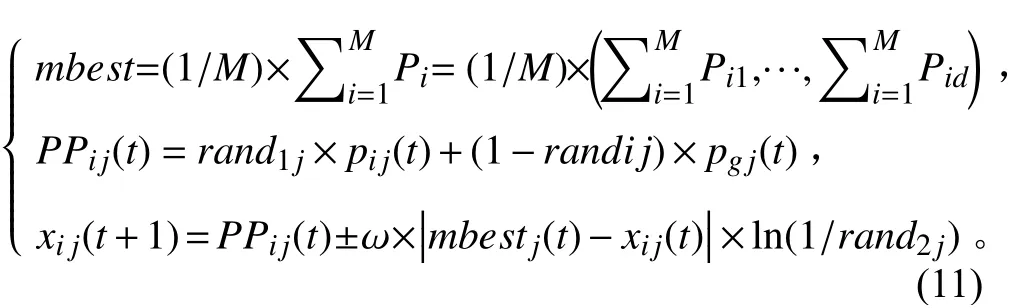
式中:和是0~1均匀分布的随机数;P为第个粒子所经历的最佳位置,P=(p,···,p);P为全部粒子所经历的最佳位置,P=(,···,g);是粒子 群的中间位 置向量;为和之间的随机点;为收敛系数,随迭代次数的变化而变化,取=0.5+0.5×(-),其中,为迭代代数,为当前迭代代数。
2.3 初始解的生成
在布局问题中,为了得到更好的求解结果和效率,设计出了大量的基于不同策略的算法,较为经典的如BL(bottom-left)和BLF(bottom-left-fill)等。这种算法对于二维装箱问题有较强的适用性,但是对于船舶的舱室布局而言,其布置的原则不是以舱室设备的最小占用面积为主要考虑指标,此外在布局过程中还需考虑设备之间的复杂约束以及某些设备必须安装在特殊区域,因此,需要探索适用于船舶舱室布局问题的方法,以提高初始解的生成质量。
借鉴文献 [14]中对三维空间分割进行初始解生成的思路,本文对二维舱室进行分割,根据舱室布置要求,对舱室某个设备放置后,将剩余空间进行分割,如图1所示。对空间进行分割后,依次选择待布置设备,判断分割后的空间能否满足待布置设备的布设;在满足装备能够布置的区域中随机选择某个区域,并在该区域中将待布置设备随机布放,完成设备的布置后,对剩余可布置空间进行更新,如图2所示。依次选取剩余设备,进行设备的布置,直至全部设备布放完毕。舱室设备的布置流程如图3所示。
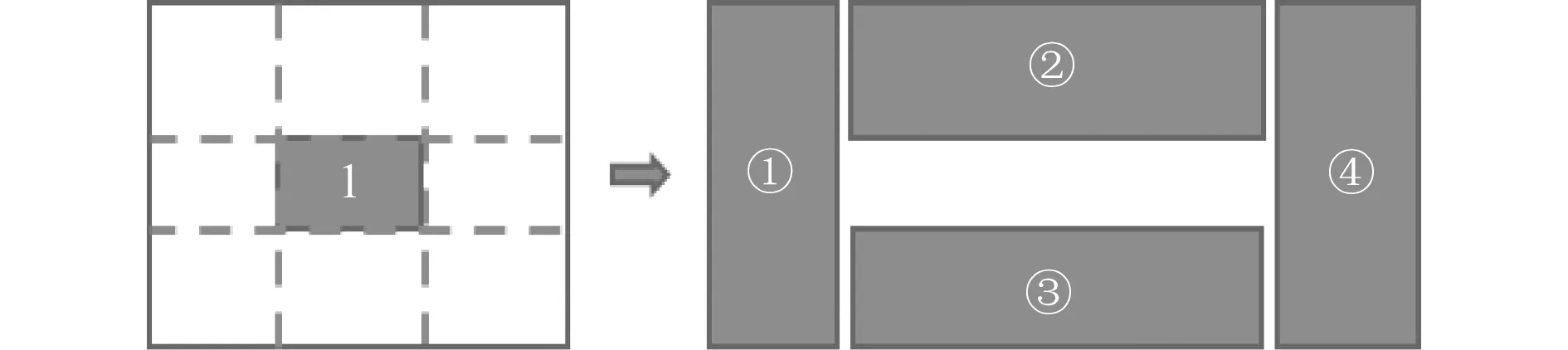
图1 空间分割示意图Fig. 1 Schematic diagram of space division

图2 依次选取设备进行布置并更新剩余空间编号Fig. 2 Select the equipment in turn for layout and update the number of remaining space
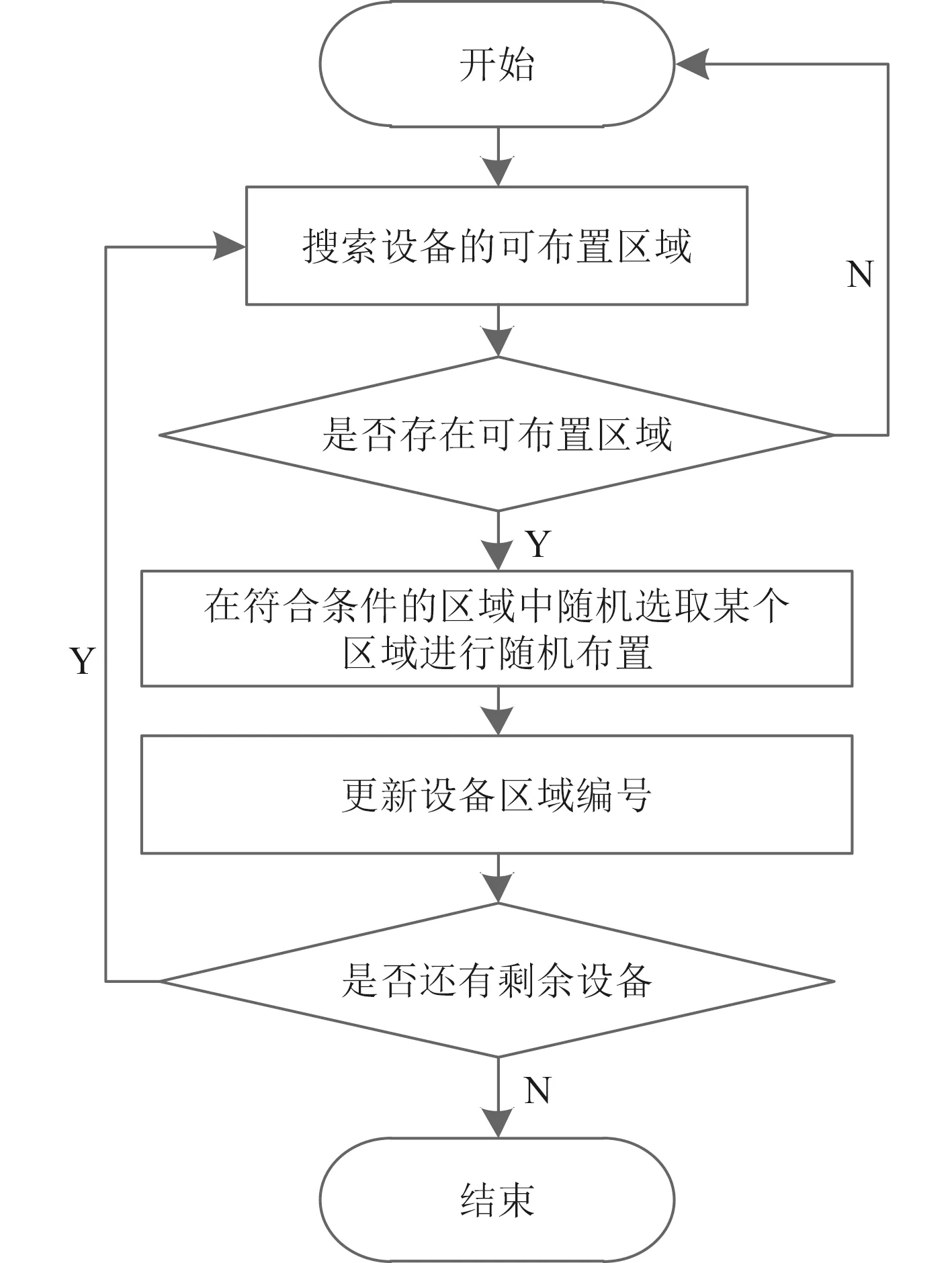
图3 初始解生成流程图Fig. 3 Flow chart of initial solution generation
2.4 计算步骤
运用量子粒子群算法求解布局问题,其计算步骤如下:
1 初始化量子粒子群算法的各项参数:种群规模、进化代数。
2 随机生成种不同的机舱设备布局方案,根据建立的数学模型,求解种群中粒子的适应度。
3 根据步骤2中所得结果,利用量子粒子群算法对粒子进行更新,并检验所得粒子中的各设备之间是否存在干涉,若存在干涉,则执行步骤4,否则跳到步骤5。
4 若存在干涉,找出干涉设备并寻找区域重新布置,若无法布置,则生成新的粒子并加入种群中进行迭代
5 若不存在干涉,计算新的粒子适应度,并执行粒子的更新操作,直到迭代结束。最终得到优化后的最优解。
3 实例分析与算法比较
选用某型船舶机舱为例,进行算法的验证。已知该型船长为6.75 m,宽为3 m,初稳性高为0.8 m,舱室设备原始布置情况及维修需求如表1所示。根据相关规范与标准,设备的布置类约束如表2所示。
设置种群=800,最大迭代次数=2 000,运用量子粒子群算法,对舱室的布置进行优化,其优化后的结果与适应度变化曲线分别如图4所示。
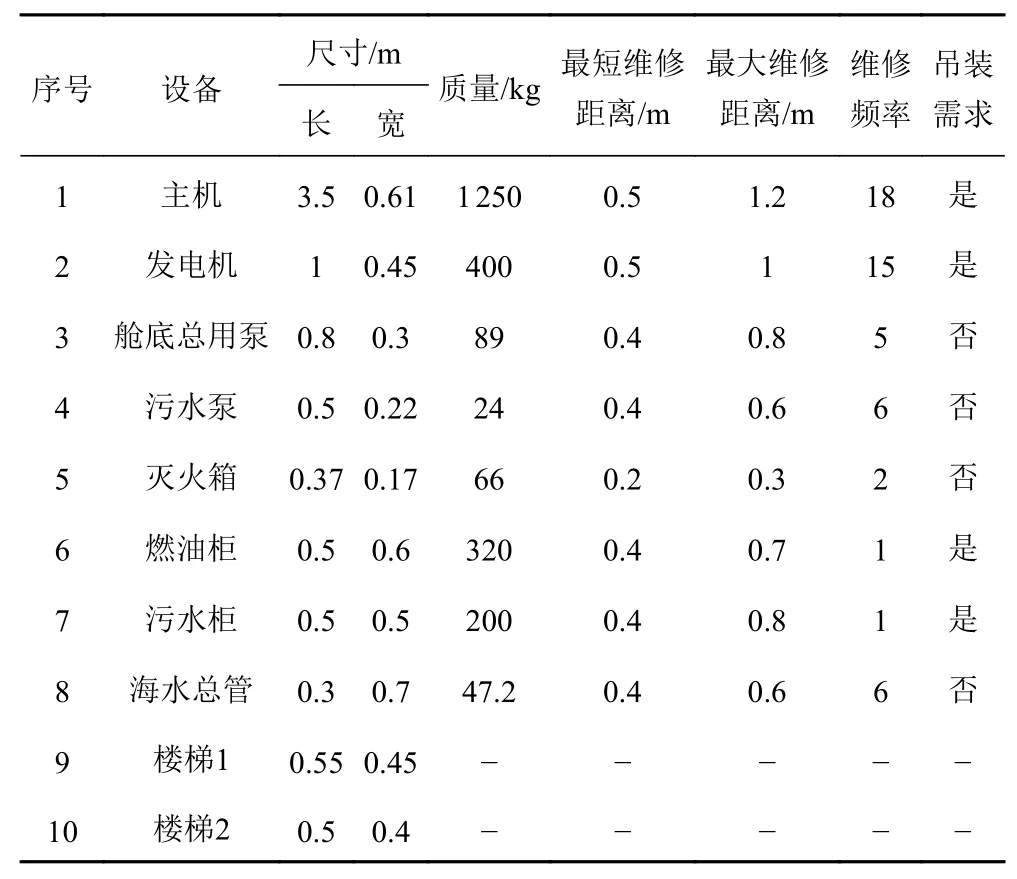
表1 舱室设备原始布置及维修需求表Tab. 1 Original layout and maintenance requirements of cabin equipment
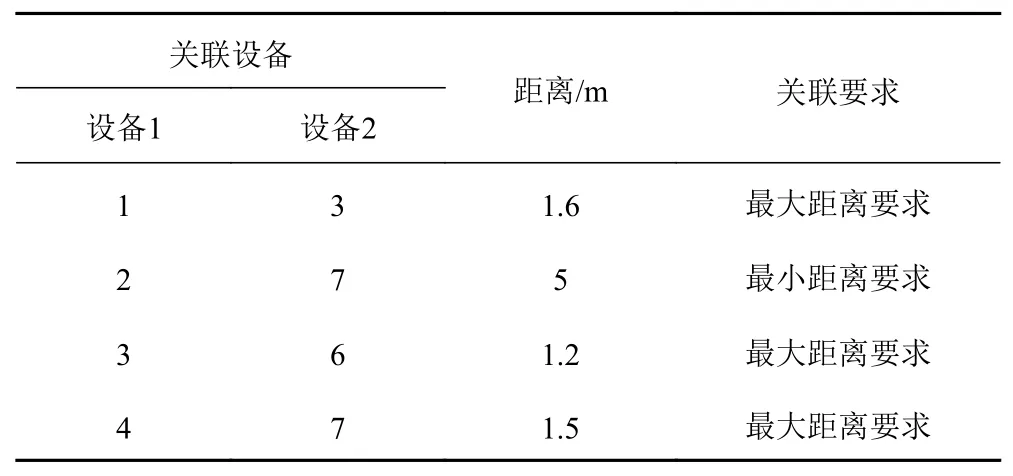
表2 设备关联性要求Tab. 2 Equipment relevance requirements
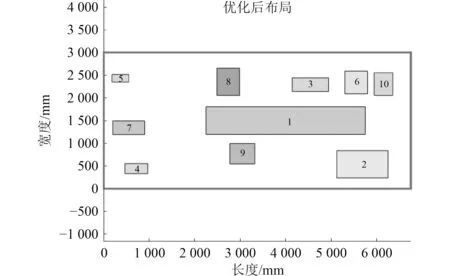
图4 基于量子粒子群算法的机舱设备布局结果Fig. 4 Layout results of cabin equipment based on quantum particle swarm optimization algorithm
同样条件下,分别运用遗传算法(设置遗传算法的=0.8,=0.01)和粒子群算法(设置惯性权重=0.8,学习因子均设置为0.8)对上述案例进行优化,所得的布局结果如图5和图6所示。将3种算法的适应度变化进行对比,如图7所示。从优化的效果看,量子粒子群算法>遗传算法>粒子群算法。各算法的目标函数值如表3所示。

图5 基于遗传算法的机舱设备布局结果Fig. 5 Engine room equipment layout results based on genetic algorithm
此外,文献 [4]中的粒子群算法的优化效果优于遗传算法效果的结论,在本文中并不成立。因此,对于船舶舱室的布局问题,需要针对具体算法与初始解的生成方式进行具体分析,进而得到相应的结论。
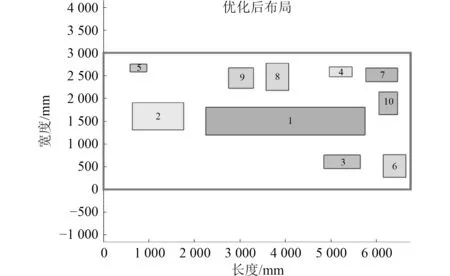
图6 基于粒子群算法的机舱设备布局结果Fig. 6 Layout results of cabin equipment based on particle swarm optimization algorithm
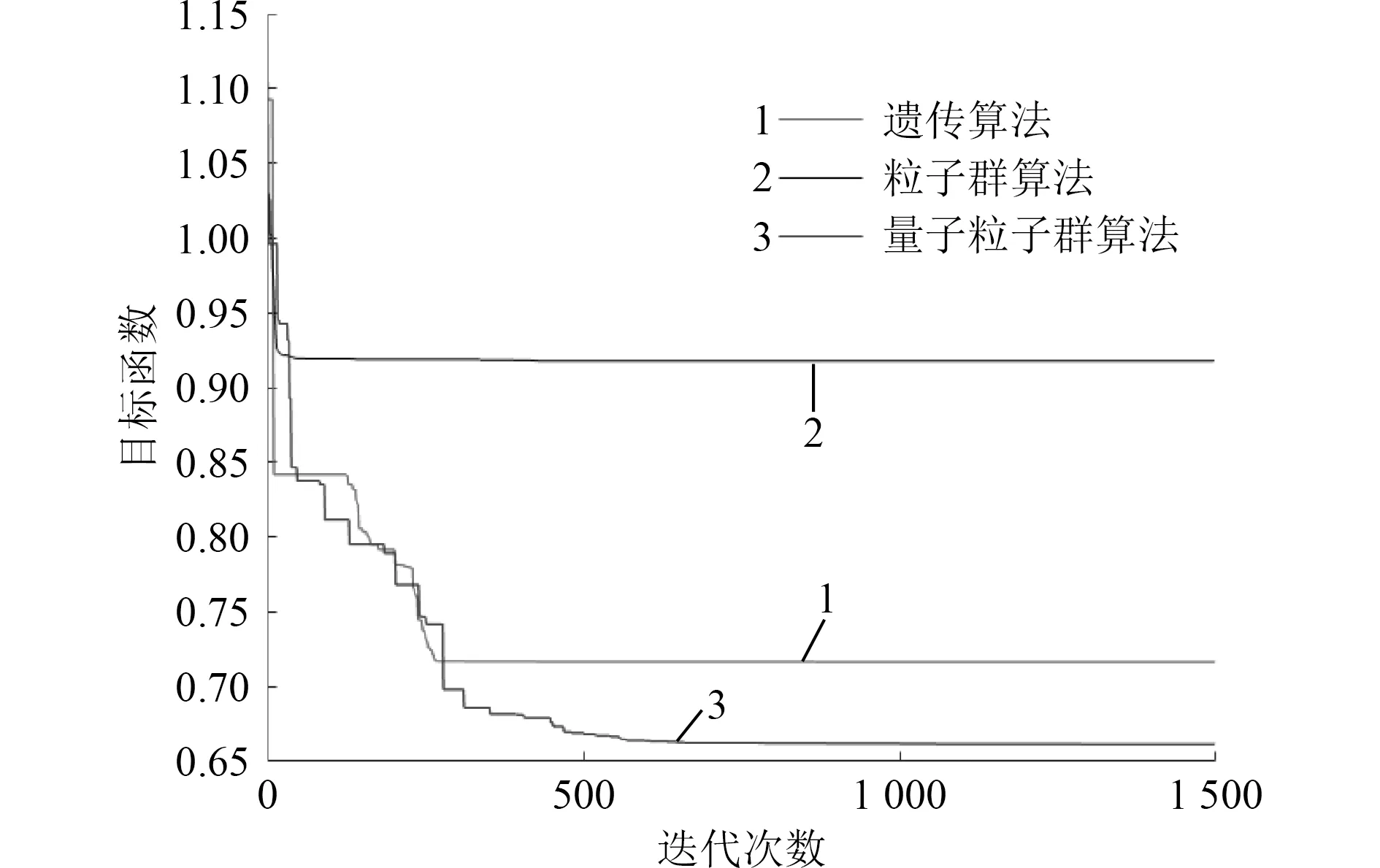
图7 不同算法的适应度变化Fig. 7 Fitness changes of different algorithms
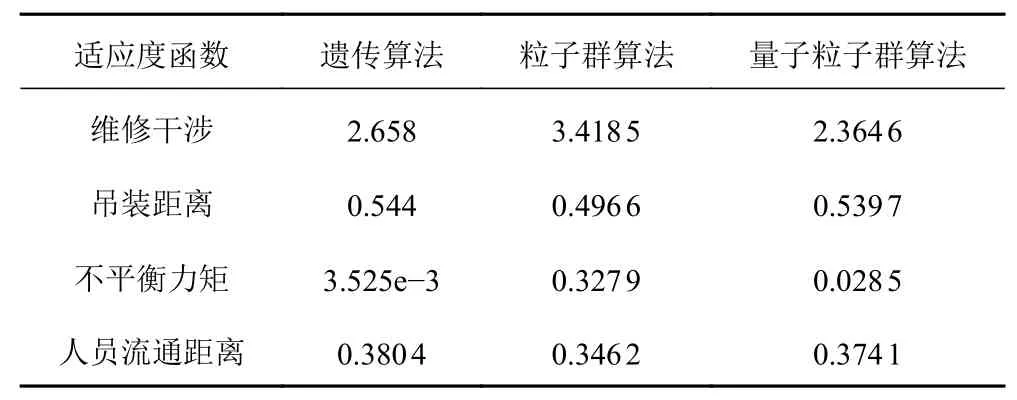
表3 不同算法下的优化效果比较Tab. 3 Comparison of optimization effects under different algorithms
4 结 语
1)研究船舶舱室的布局问题时,并不能单纯得出某种智能算法更优的结论,需要将启发式算法与元启发式算法相结合,得到计算结果,进而讨论算法的优劣性。
2)对于机舱布局,在运用本文初始解生成方式的前提下,量子粒子群算法的计算结果优于遗传算法和粒子群算法。
本文研究结果可为船舶机舱的布置与优化提供参考方案。
在后续研究中,主要从3个方面进一步研究:一是布局问题初始解生成的生成与规划的问题;二是各类智能算法的改进与优化在布局算法中的应用;三是布局问题的元启发式算法与启发式算法相结合与匹配的问题。
