长管路均压移水系统水力特性数值分析与试验研究

张 政，肖龙洲，俞 健，蔡标华，邹雨静(武汉第二船舶设计研究所，湖北 武汉 430064)

0 引 言

在海上长时间航行的船舶，由于受海流、海浪以及海风等因素的影响，航行的平稳性难以避免会受到影响，为保证船舶具有较好的运行平稳性与操作性，船舶上设有移水系统，通过2个水箱之间的移水从而实现浮力调节，进而保证船舶运行的平稳性、操作性和安全性。

马士虎建立移水系统的数学模型，确定了仿真软件以及技术接口的组成，最终确立了其程序框图。朱靖宇提出移水系统的设计方案以及本地电动、本地自动和遥控3种控制系统的研制方案。蔡标华通过AMEsim软件建立移水系统的模型，分析发现水锤峰值一般发生在阀门附近，且延长阀门关闭时间有助于减小移水系统水锤的产生。李斌在其基础之上通过Flowmaster瞬态仿真对移水系统水锤抑制的方法进行了研究，研究发现两阶段关阀策略以及加装蓄能元件均能较好的抑制水锤。彭利坤通过AMEsim软件建立了球阀模型，用于研究移水系统气移水时管路的冲击特性，发现阀后加装蓄能器和缩短管长均有助于减小压力冲击，阀门线性关闭规律相较正弦关闭规律所产生的压力冲击峰值更小。前述的数字模型与仿真软件分析对移水系统的管路特性、水锤与冲击效应做了充分研究，在移水系统的减振降噪方面发挥了巨大作用，但是鲜有针对均压移水系统水力特性的研究。

针对船舶移水系统存在管路长、流量大、存在背压等问题，本文建立均压移水系统F l o w m a s t e r模型，通过将移水系统中两水箱排气孔相连组成均压移水系统，通过仿真对均压移水系统关阀后系统水力特性进行研究，并设计试验验证仿真结果的正确性。

1 均压移水系统建模、仿真与试验

1.1 均压移水系统基本原理

均压移水系统原理图如图1所示。均压移水系统共有水回路与气回路2条回路。

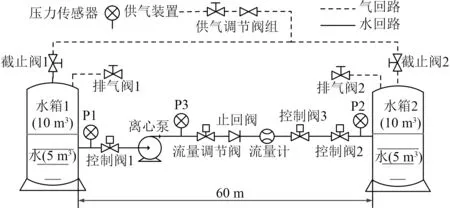
图1 均压移水系统原理图Fig. 1 Schematic diagram of pressure-balancing water conveying system

其中水回路的核心元件分别为离心泵，水箱1和水箱2。水箱1和水箱2模拟实际船舶结构中的2个水箱，两水箱的容积均为1 0 m，每个水箱内初始装有5 m的水，两水箱之间的管路长度为 60 m。离心泵负责为均压移水系统提供动力，将水箱1中的水增压后输送至水箱2。另外水回路中还有控制阀、流量调节阀、单向阀、流量计和压力传感器等辅助元件。

气回路的核心元件为供气装置以及供气调节阀组，负责为水箱1和水箱2充压，初始压力为0 .25 MPa，气回路管路公称直径为15。另外气回路还包括排气阀和截止阀等元件，通过将两水箱顶部出气口连通，改善水箱因移水而产生的气压不平衡现象。

1.2 均压移水系统运行工况

均压移水系统根据控制阀3的开闭情况分为均压移水与均压平衡2个工况。

当控制阀3完全关闭前，水回路与气回路均保持连接状态时，系统进入均压移水工况。水箱1中的水从水回路经离心泵增压后流入水箱2中，此时因为水箱1中有水流出、水箱2中有水流入，因此水箱1中气压降低、水箱2中气压升高，两水箱内气压不平衡导致水箱2中气体通过气回路进入水箱1中。具体流动情况如图2所示。当控制阀3完全关闭后，水回路断开气回路保持连接，系统进入均压平衡工况。此时两水箱内仅有气体流动而无水流动，因此两水箱内的气压会逐步趋于一致。具体流动情况如图3所示。

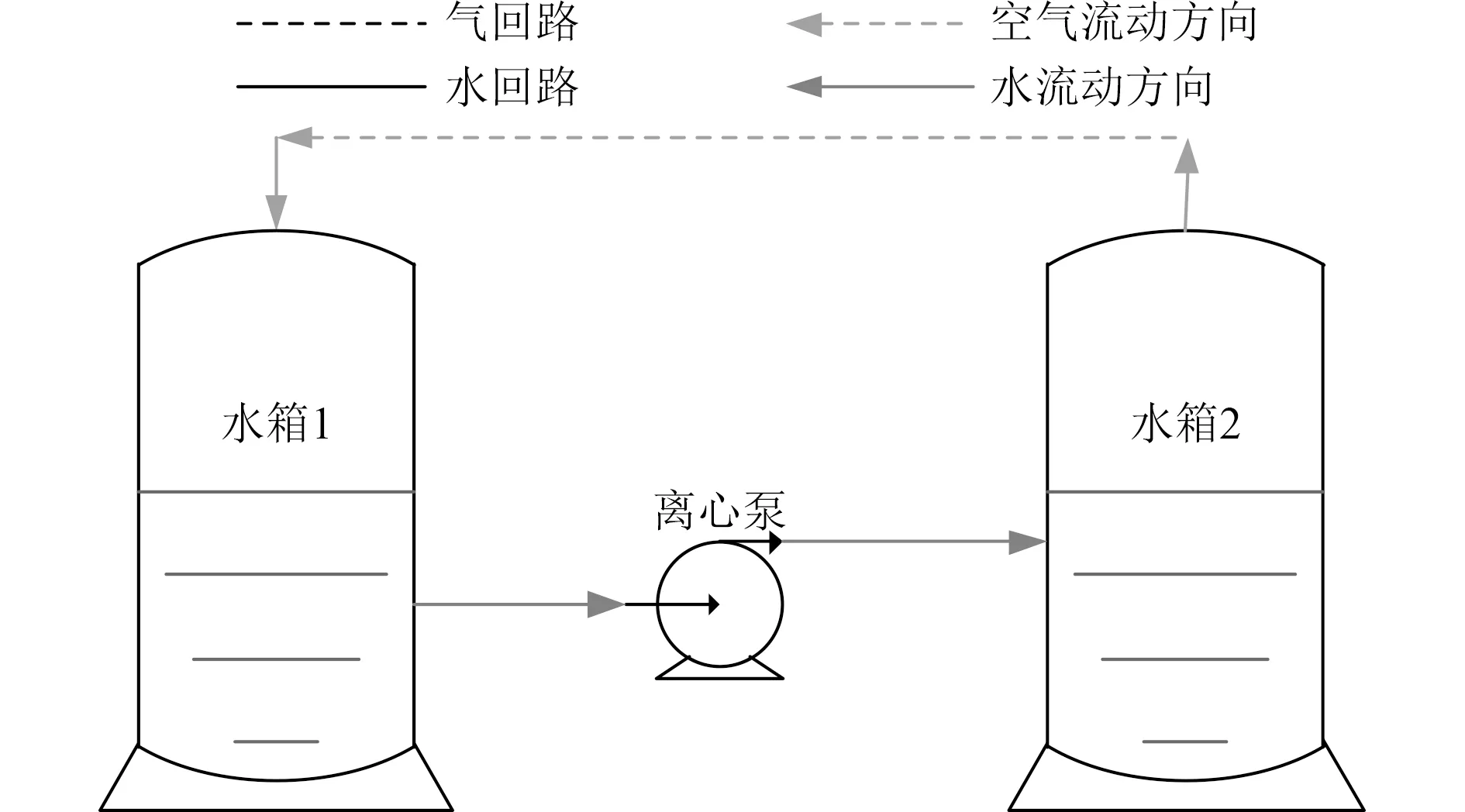
图2 均压移水工况Fig. 2 Pressure-balancing water conveying operation condition

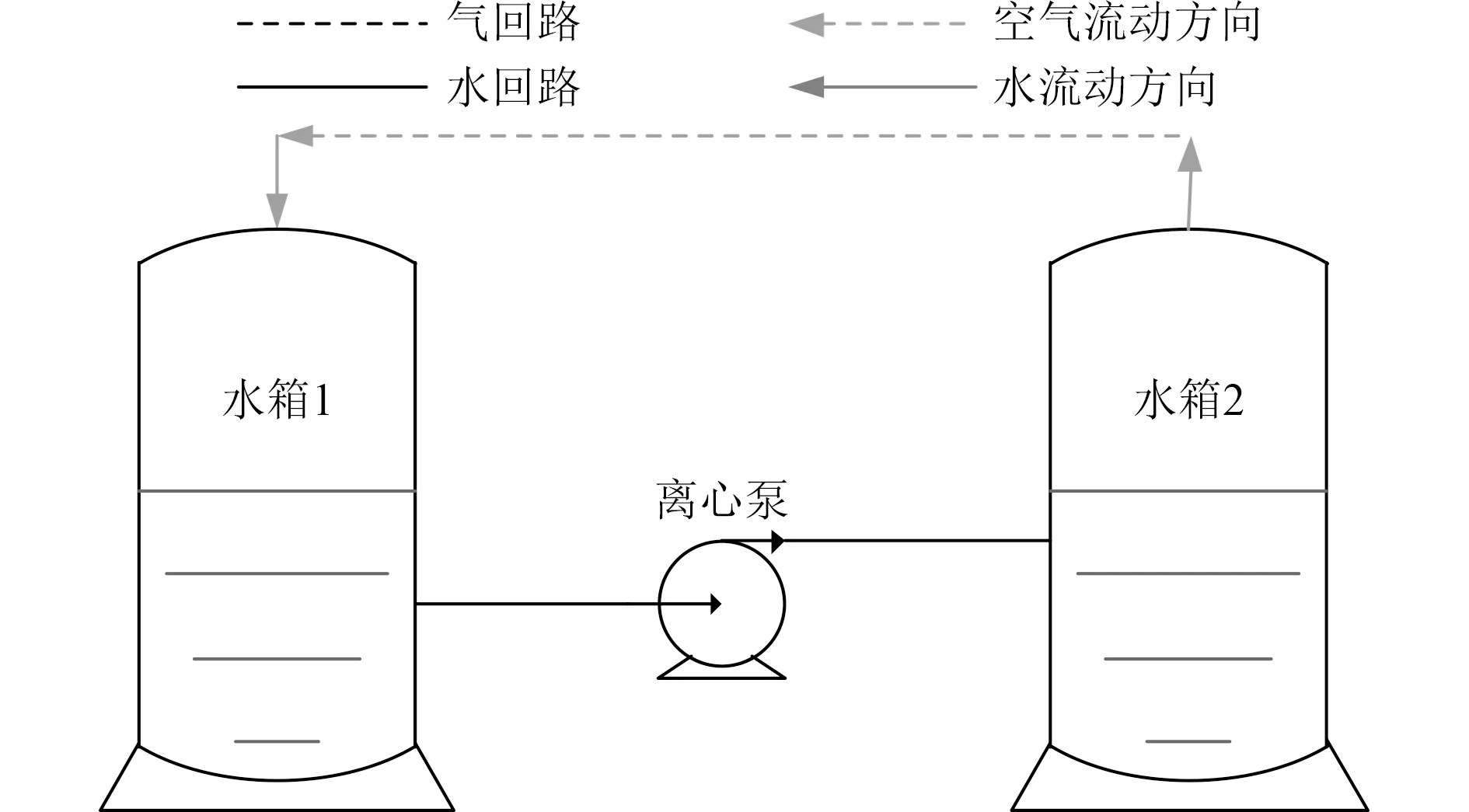
图3 均压平衡工况Fig. 3 Pressure-balancing air proportion operation condition

1.3 均压移水系统仿真建模

1.3.1 Flowmaster仿真模型

依据图1，在Flowmaster中建立如图4所示均压移水系统模型。

在Flowmaster模型中，元件1、元件2、元件3、元件6分别表示水箱1、水箱2、离心泵和控制阀3，分别用表示供气装置初始压力（图中元件12处压力），表示水箱1出口压力（节点9处压力），表 示水箱2入口压力（节点5处压力），表示泵出口压力（节点1处压力）。水箱1右侧与水箱2左侧管路为气回路，水箱1左侧与水箱2右侧之间管路为水回路。元件7、元件8、元件9、元件10、元件11所用阀的初始开度为1，元件4和元件6所用控制阀开度为0。仿真开始后水箱1和水箱2中气压与元件12相同。通过控制器13将元件11的开度调至0，随后通过控制器14启动离心泵，再通过控制器16将元件6的开度调至1，并通过控制器15逐步增大元件4的开度至1，系统运行一段时间后，通过控制器15将阀门4开度调至0，随后通过控制器14停泵。Flowmaster计算模式为可压缩瞬态，时间步长为0.1 s，总时长为500 s。

图4 均压移水系统Flowmaster模型Fig. 4 Flowmaster model of pressure-balancing water conveying system

1.4 均压移水系统均压移水试验

试验开始前，水箱1和水箱2中装有 5 m的水，确认截止阀1和截止阀2与控制阀1和控制阀2处于全开状态，供气调节阀组处于关闭状态。

试验开始后，打开供气调节阀组向水箱1和水箱2供气均压，当两水箱内气压达到 0.25 MPa时停止供气，并关闭供气调节阀组。启动离心泵，待其出口压力稳定后，打开控制阀3，并逐渐打开流量调节阀，并观察流量计，当流量增大至 60 m/h时，停止调节流量调节阀，待系统稳定运行一段时间后，观察系统运行状态，并记录相关参数。最后关闭控制阀3，并停止运行离心泵，系统进入均压平衡工况并观察关阀过程中系统的运行状态，并回复试验台架至初始状态。

2 结果与讨论

2.1 仿真结果与试验验证

图5为均压平衡工况下仿真与试验结果对比。试验过程中为防止管路出现严重的水锤效应对系统元器件产生破坏，将关阀时间设为5 s。可知，，，在均压平衡工况下的仿真结果与试验数据符合较好，试验结果验证了仿真的正确性。

2.2 均压移水系统水力特性分析

2.2.1 均压移水工况下管路系统压力分布

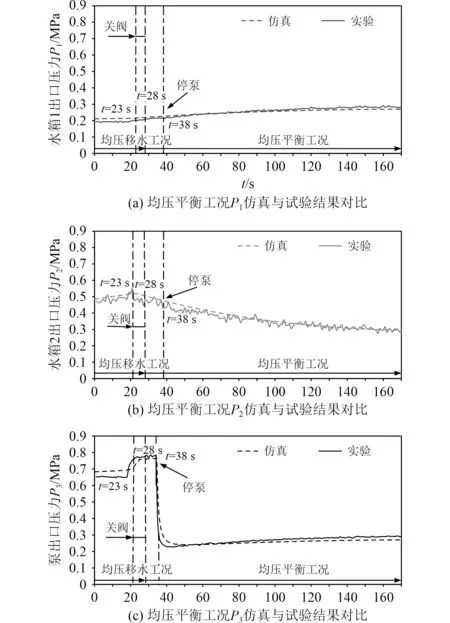
图5 均压平衡工况仿真与实验结果对比（P0 = 0.25 MPa）Fig. 5 Comparison of simulation and experimental results under pressure-balancing air proportion operation condition（P0 = 0.25 MPa）

图6为根据仿真结果绘制的在均压移水工况下150 s时管路系统不同位置压力分布曲线，其中水回路压力分布曲线包含，，，泵入口压力以及水箱1和水箱2液面压力；气回路压力分布曲线只包含水箱1和水箱2液面压力。均压移水工况150 s时系统处于均压移水工况，水回路与气回路均保持连接，此时水箱1与水箱2之间存在压力差。

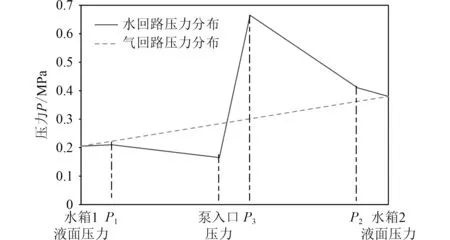
图6 管路系统不同位置压力分布（均压移水工况，P0 = 0.25 MPa）Fig. 6 System pressure distribution （pressure-balancing water conveying operation condition, P0 = 0.25 MPa）

在水回路中，由于水箱1中水压的影响，相较水箱1液面压力略有升高。由于水回路管路存在沿程损失因此泵入口处压力相较有所降低，经过离心泵增压，相较泵入口压力大幅升高。同样，由于管路存在沿程损失因此相 较降低。最后由于水箱2中水压影响，水箱2液面压力相较有所降低。

在气回路中，水箱2到水箱1中仅有沿程损失没有增压元器件，因此直接将水箱2液面压力与水箱1液面压力相连，水箱2液面压力高于水箱1液面压力。

2.2.2 均压平衡工况压力变化

图7为均压移水系统均压平衡工况压力变化曲线。在=18 s前，阀门尚未完全关闭，系统仍处于均压移水工况，系统中水回路与气回路保持连接，离心泵将水箱1内的水增压后输送至水箱2中，水箱2中气压大于水箱1中气压因此水箱2中气体通过气回路流入水箱1中，这使得减 小，增 大，减小。在=18 s 时，阀门完全关闭，达到最大值 0 .55 MPa，达 到最小值 0.19 MPa ，同时由 0 .65 MPa快速提高至0.78 MPa ，并在停泵前一直维持不变。在=18 s后，系统进入均压平衡工况，水回路断开而气回路仍然保持连接，两水箱之间没有水流动，但是两水箱之间仍存在气压不平衡，这使得水箱2中的气体流入水箱1中，因此关阀后一 直增大，一直减小，直到最后两水箱内气压一同到达 0.28 MPa并维持不变，即两水箱达到压力均衡。在 停泵后压力快速掉落至与相同，为 0.22 MPa ，并在随后的时间内同一同增大，最后一起达到 0 .28 MPa，实现压力均衡。

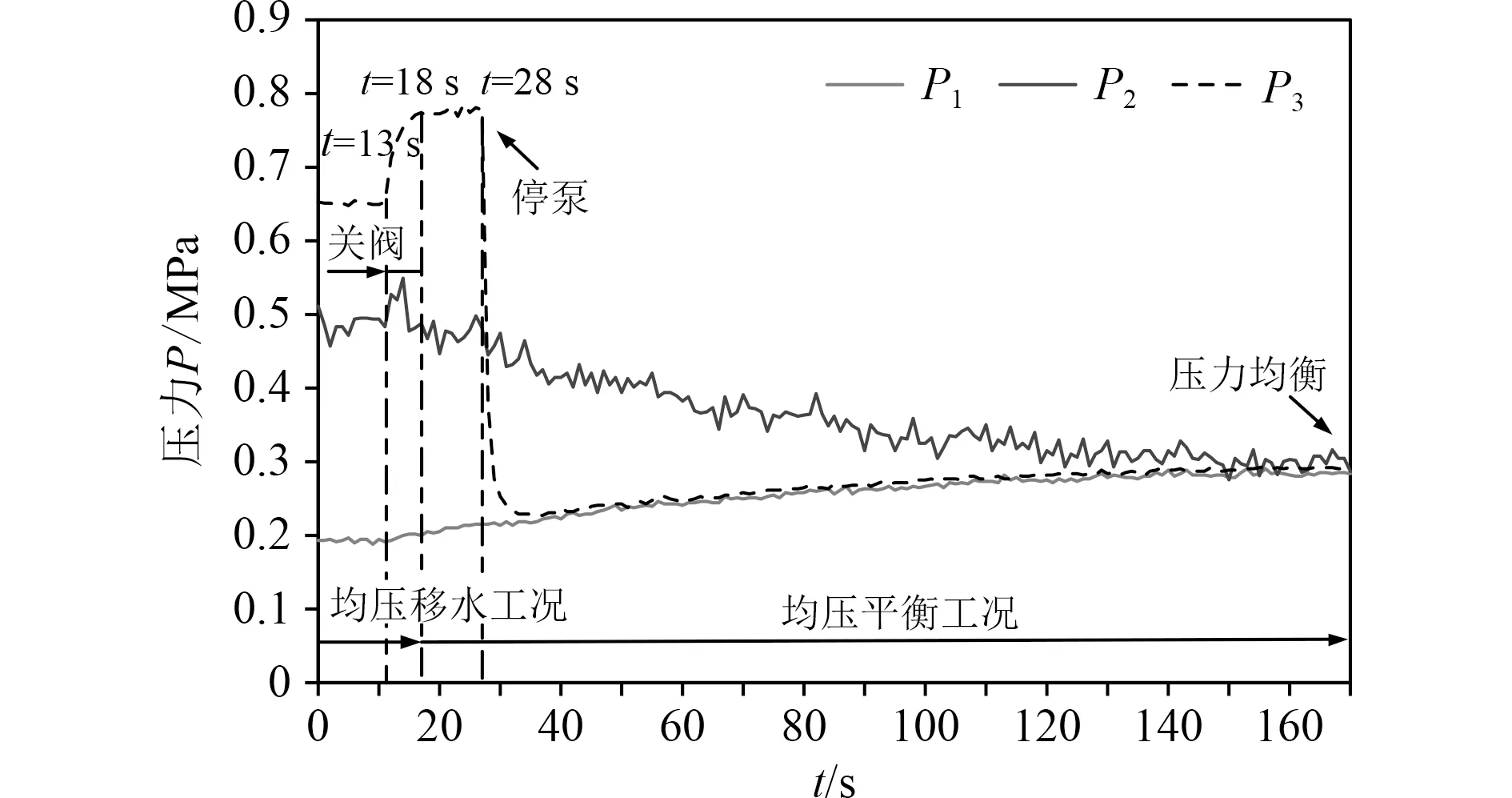
图7 均压平衡工况压力变化（P0 = 0.25 MPa）Fig. 7 Pressure change under pressure-balancing air proportion operation condition (P0 = 0.25 MPa)

2.3 均压移水系统不同初始压力仿真

为探究均压移水系统不同初始压力对系统均压平衡工况的影响，通过Flowmaster软件仿真系统初始压力分别为 0.1 MPa ， 0 .25 MPa 与 0.4 MPa时系统均压平衡工况，不同初始压力下均压平衡工况和如图8所示，不同初始压力下均压平衡工况泵入口压力如图9所示。

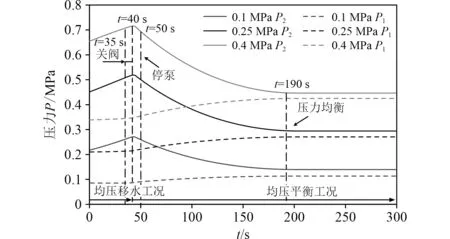
图8 不同P0时均压平衡工况P1和P2Fig. 8 Pressure-balancing air proportion operation condition P1 and P2 under different P0

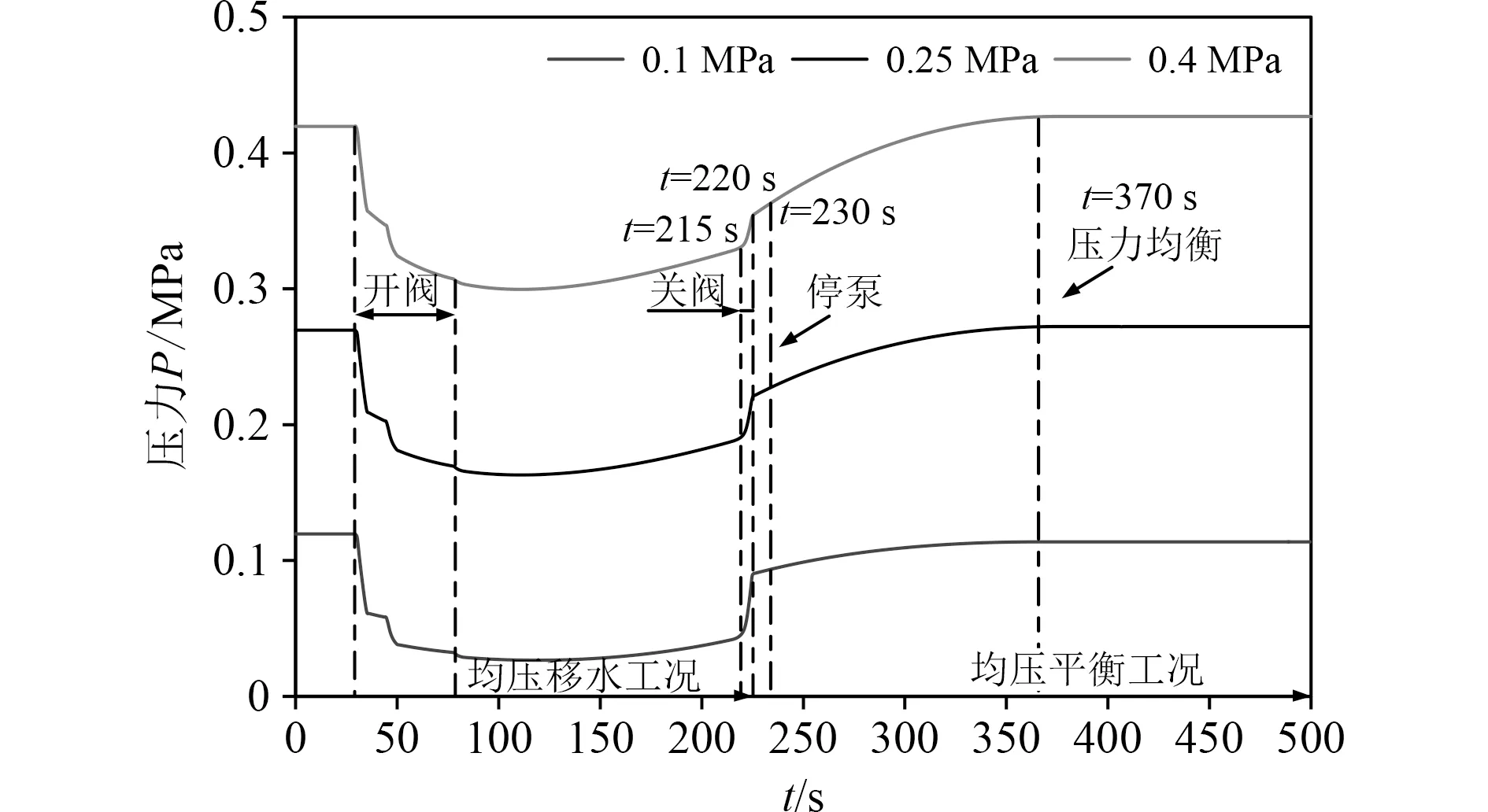
图9 不同P0下泵入口压力Fig. 9 Pump inlet pressure under different P0

根据图8可知，在=40 s 前，阀门尚未完全关闭，系统仍处于均压移水工况，水回路与气回路均保持连接，水箱1和水箱2之间有水与气流动，此时3种初始压力下均 在增大、略有增大，且初始压力越大，和越大；在=40 s后，阀门完全关闭，系统进入均压平衡工况，系统水回路断开气回路保持连接，水箱1和水箱2之间无水流动但水箱2中气体仍流入水箱1中，此时3种初始压力下均在减小、均 在增大，直到=190 s 时达到3种初始压力，和同时达到压力均衡状态，压力随后保持不变，3种初始压力系统停泵后达到压力均衡所用时间均为1 50 s。

因此初始压力主要影响和的大小，且初始压力越大，和相应地就会越大，但不同的初始压力下系统到达压力均衡的时间一样。

图9为均压移水系统整个仿真过程中泵入口压力曲线变化图。可知，不同初始压力下，初始压力越大，泵入口压力越大。由于在开阀阶段泵口压力持续降低，因此初始压力越小，泵越容易产生气蚀，从而对泵的性能产生影响。当初始压力为 0 .1 MPa时，阀完全打开时泵入口压力最低仅为 0.03 MPa；而初始压力为 0.4 MPa时，阀完全打开时泵入口压力最低可达0.3 MPa，泵更不易产生气蚀。因此初始压力越大越有助于抑制气蚀的产生。

2.4 均压移水系统气回路不同管径仿真

为探究均压移水系统气回路管路不同管径对系统均压平衡工况的影响，通过Flowmaster软件仿真气回路管路公称直径分别为10，15与20 时系统均压平衡工况，不同管径下均压平衡工况和如图10所示。

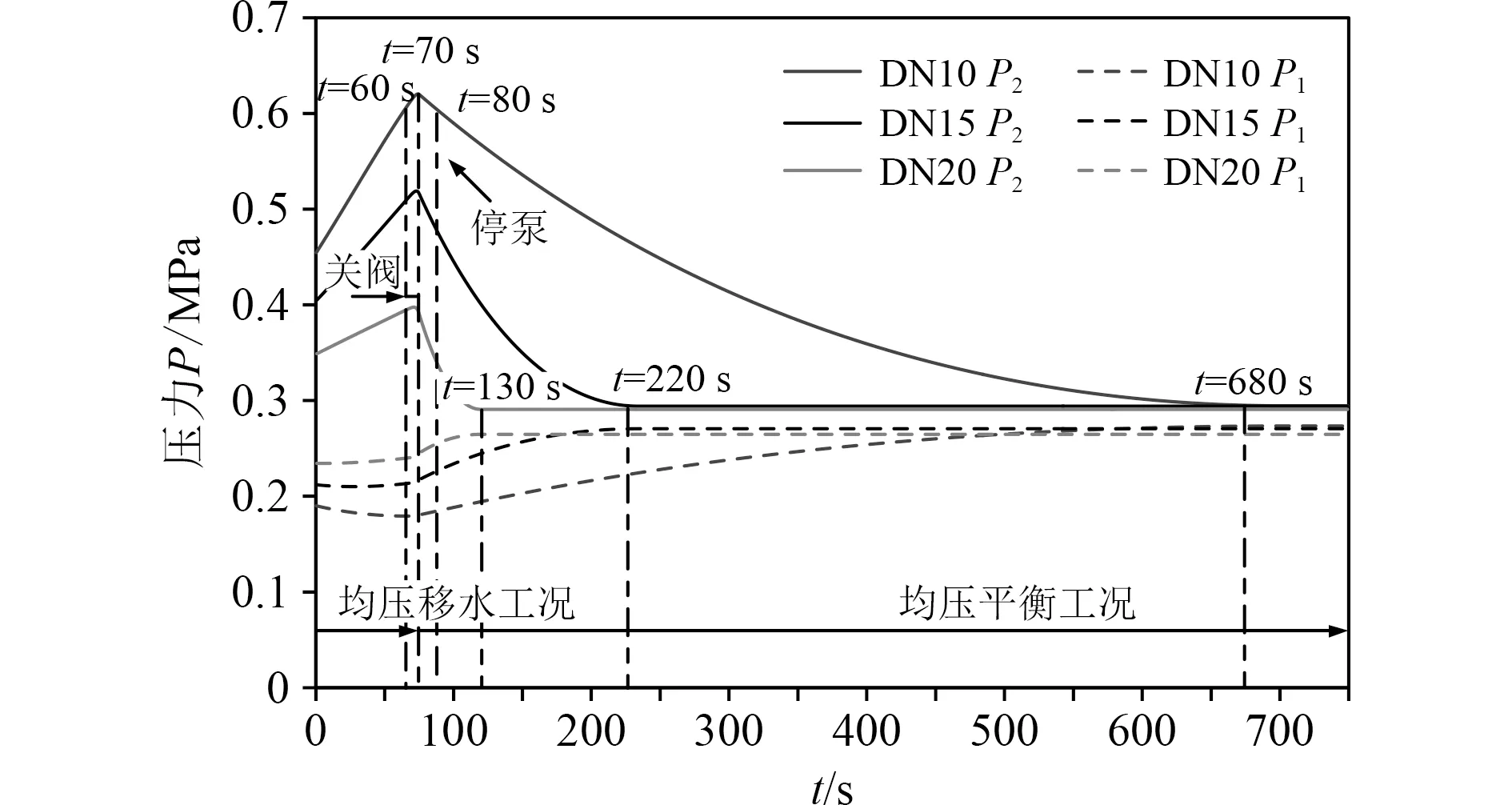
图10 不同管径下气回路均压平衡工况P1和P2(P0 = 0.25 MPa)Fig. 10 Pressure-balancing air proportion operation condition P1 and P2 under different pipe diameters(P0 = 0.25 MPa)

可知，在=70之前，阀门尚未完全关闭，系统处于均压移水工况，水回路与气回路均保持连接，水箱1和水箱2之间有水与气流流动，此时3种管径下均在增大、略 有增大，其中管径越大的越 小、越大，即和之 间压差越小；在=70 s后，阀门完全关闭，系统进入均压平衡工况，水回路断开气回路保持连接，水箱1和水箱2之间无水流动但水箱2中气体仍流入水箱1中，此时3种管径下均在减小、均在增大，但不同管径下压力变化的速度不同，管径越大不仅压差越小，压力变化速度也越快，因此到达压力均衡所用时间越短：20 在=130 s时就达到压力均衡状态，用时 60 s；15 在=220 s达到压力均衡状态，用时1 50 s ； DN10在=680 s时才达到压力均衡状态，用时 610 s。但最终3种管径达到压力均衡时的压力相同。

因此不同管径不仅影响和的大小，管径越大，在关阀前越 大且越 小，和之间的压差越小；而且会影响系统到达压力均衡的时间，管径越大，到达压力均衡的时间越短，但不会影响最终水箱内压力值。

3 结 语

本文通过将船舶移水系统中两水箱排气孔相连从而组成均压移水系统，用Flowmaster软件对均压移水系统的水力特性进行仿真，并通过试验验证仿真结果的正确性，得出以下结论：

1）关阀后系统进入均压平衡状态，由于水回路断开气回路保持连接，和会 逐步趋于一致，会在停泵后下降至与相同大小，并最终达到压力均衡。

2）随着系统初始压力的 增大，和和泵入口处压力增大，有助于抑制泵的气蚀，但初始压力的变化不会影响系统达到压力均衡的时间。

3）随着系统气回路管径的增大，关阀前减小增 大，且-减小，在关阀后系统到达压力均衡的时间减小。