基于深度学习的双耳声源定位算法研究

宋 昊，刘雪洁，俞胜锋，钟小丽

(1.广东工业大学管理学院，广东广州 510000；2.华南师范大学物理与电信工程学院，广东广州 510006；3.华南理工大学物理与光电学院，广东广州 510640)

0 引言

在双耳听觉中，人类能够通过接收到的双耳声信号反推出声源的空间方位，即实现双耳声源定位。研究表明，双耳声源定位的主要因素包括耳间差异：包括双耳时间差(Interaural Time Difference,ITD)、双耳声级差(Interaural Level Difference,ILD)和单耳谱特征[1-2]。通常，ITD是低频声源的主要定位因素，ILD是中、高频声源的主要定位因素，而单耳谱特征对于中垂面以及混乱锥定位至关重要。由于现实声场景的复杂性，准确的声源定位往往是多种定位因素综合作用的结果[3]。

已有的双耳声源定位模型分为两大类：基于听觉系统的模型和基于机器学习的模型[4]。前者通过较为详尽地再现声信号传输和分析生理和心理过程，从而达到模拟人类声源定位功能的目的。然而，受限于声源定位的生理和心理过程的研究进展，目前基于听觉系统的双耳声源定位模型只能表征较为简单的声场景，例如基于谱因素的中垂面定位[4-5]。本质上，双耳声源定位是一种基本的大脑机能，因此基于机器学习(即采用计算机模拟人脑行为)的双耳声源定位模型得到了重视[6]。Gill等[7]将单耳谱特征输入单隐层(含9个神经元)前馈型神经网络，以预测声源的仰角方位。Chung等[8]以ITD和单耳谱特征作为输入，采用浅层全连接后向传播神经网络(Back Propagation Neural Network,BPNN)预测声源的空间方位。Jin等[9]先采用耳蜗模型提取双耳定位因素，再采用浅层时延神经网络预测声源的空间方位。可见，已有基于神经网络的定位模型通常以定位因素作为模型输入进行训练和预测。由于声源定位是多种定位因素综合作用的结果，且不同声场景下这种综合作用可能不同，目前对其尚无定论。因此，以定位因素作为模型输入的定位模型需要较完备的先验知识，且模型适用性取决于定位因素的选取。此外，已有基于神经网络的定位模型属于全连接的浅度学习(即只包含一个或者两个隐层)，这制约着预测效果的提升。随着计算机计算能力以及数据量的提升，同时受益于神经生物学家对动物大脑解剖研究的成果，2006年Hinton等[10]提出了深度学习的概念。深度学习源于机器学习的范畴。相比于机器学习中各种浅层的学习模型，比如支持向量机、最大熵方法等，深度学习神经网络能表达现实中各种复杂数据的内部结构，已成为一种广泛使用的工程方法[11-12]。2019年丁建策等[13]提出了利用深度神经网络(Deep Neural Network,DNN)预测声源方位角的算法。该方法采用子带双耳特征和双耳信号互相关特征共计57维特征作为输入，取得了较好的预测效果，为后续声源距离的预测提供了可靠的信息。Ding等[14]进一步提出了多目标DNN算法。该方法提取了双耳信号中的子带特征和统计特性共计393维特征作为输入，可同时预测声源的距离和方位角；由于新算法降低了方位角变化对距离估计的影响，其距离预测的准确性高于现有的同类算法。

本文提出了基于深度学习的双耳声源定位算法，并采用完整的双耳声信号作为输入，避免了人为提取特征的繁琐过程。首先，实现了基于卷积神经网络(Convolutional Neural Network,CNN)和基于深层后向传播神经网络(Deep Back Propagation Neural Network,D-BPNN)的深度学习框架，并采用不同空间声源间隔的双耳声信号作为输入进行训练与预测，最后采用前后混乱率、定位准确率等指标比较了两种深度学习模型的有效性。

1 算法介绍

本文的声信号处理流程如图1所示。首先，将单通道声信号E0(t)分别与左右耳脉冲响应HL和HR进行卷积，合成双耳声信号EL和ER；然后，将预处理后的EL和ER输入深度神经网络进行训练；最后，采用训练好的算法模型进行预测，得到声源空间方位的分类输出(即方位预测)。

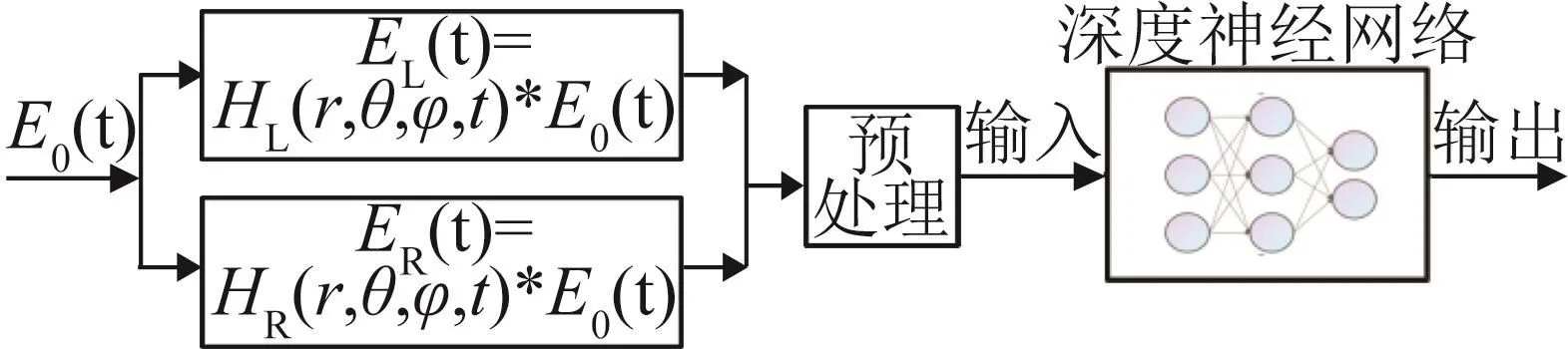
图1 声信号处理流程图Fig.1 Acoustic signal processing flow diagram

卷积神经网络CNN是一种典型的深度学习框架。目前，CNN已被广泛应用于声信号处理，例如遇险信号识别[15]、混响时间估计[16]、水下声源距离预测[17]和海床类型识别[18]等。图1中的深度神经网络主要采用CNN实现。在深度学习领域，卷积神经网络CNN和循环神经网络(Recurrent Neural Network,RNN)都是常用的处理音频信号的算法。两者的区别在于：(1)RNN具有对时间进行扩展以及多个时间输出计算的能力，而CNN能够在空间上拓展并对特征进行卷积；(2)RNN可以用于描述时间上连续状态的输出(具备记忆功能)，而CNN用于静态输出；(3)RNN的层次结构深度有限，而CNN的层数能够达到100层以上。本文的研究目标是实现对处于不同空间方位的声源的准确定位(分类)，而不考虑声信号在时间上的连续特征。因此，本文选用CNN作为实现深度学习的框架。此外，目前采用全连接后向传播神经网络BPNN的定位模型多为浅层网络。为了和CNN模型进行对比，本文通过增加隐层的层数，将浅层BPNN改进为DBPNN。因此，图1中的深度神经网络分别采用CNN和D-BPNN实现。

1.1 数据准备

以人头中心为坐标原点，建立顺时针球坐标系。定义正前方的水平方位角为0°，正右方的水平方位角为90°。

采用虚拟声技术合成双耳声信号数据库，其中双耳脉冲响应来自MIT HRTF数据库[19]。该数据库含有KEMAR人工头远场(距离声源1.4 m)710个声源空间方位的双耳脉冲响应，数据长度为512点(44.1 kHz采样,16 bit量化)。单通道声信号采用中英文混合的单声道语音信号(频段范围为150 Hz～4 000 Hz，采样频率为44.1 kHz)。首先，采用短时过零率语音端点检测算法对初始语音信号进行检测，依据检测结果将其分别截断成8 300段(100 ms每段)短时语言片段。然后，依据约10∶1的比例随机将各方位的8 300段短时语言片段划分为训练信号与测试信号。最后，根据图1中的虚拟声合成方式得到不同声源方位的双耳时域声信号。为了加快训练的收敛速度，对所有合成的双通路信号进行归一化运算，将其幅值限制在[-1，1]范围内。

为了探讨不同声源空间间隔的影响，图1中的网络输入分别采用水平面15°、30°和45°空间角度间隔的双耳声信号。表1是不同空间角度间隔时，深度神经网络所采用的数据情况。

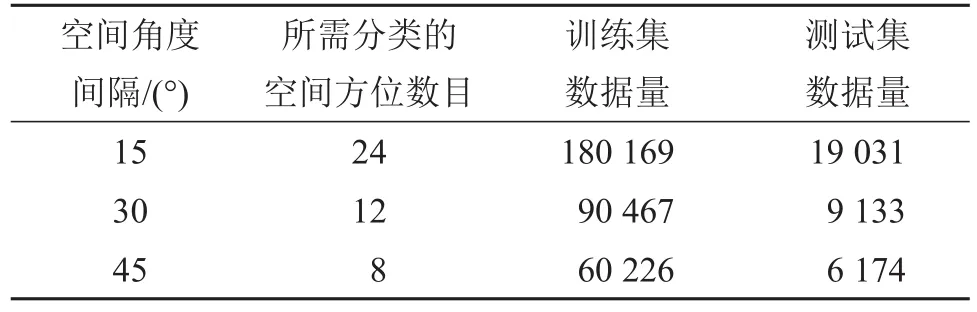
表1 深度神经网络采用的数据Table1 Data used for DNN

1.2 基于D-BPNN模型的双耳声源定位算法

D-BPNN模型主要由两个全连接层、一个随机失活层和一个扁平层组成，网络结构如图2所示。

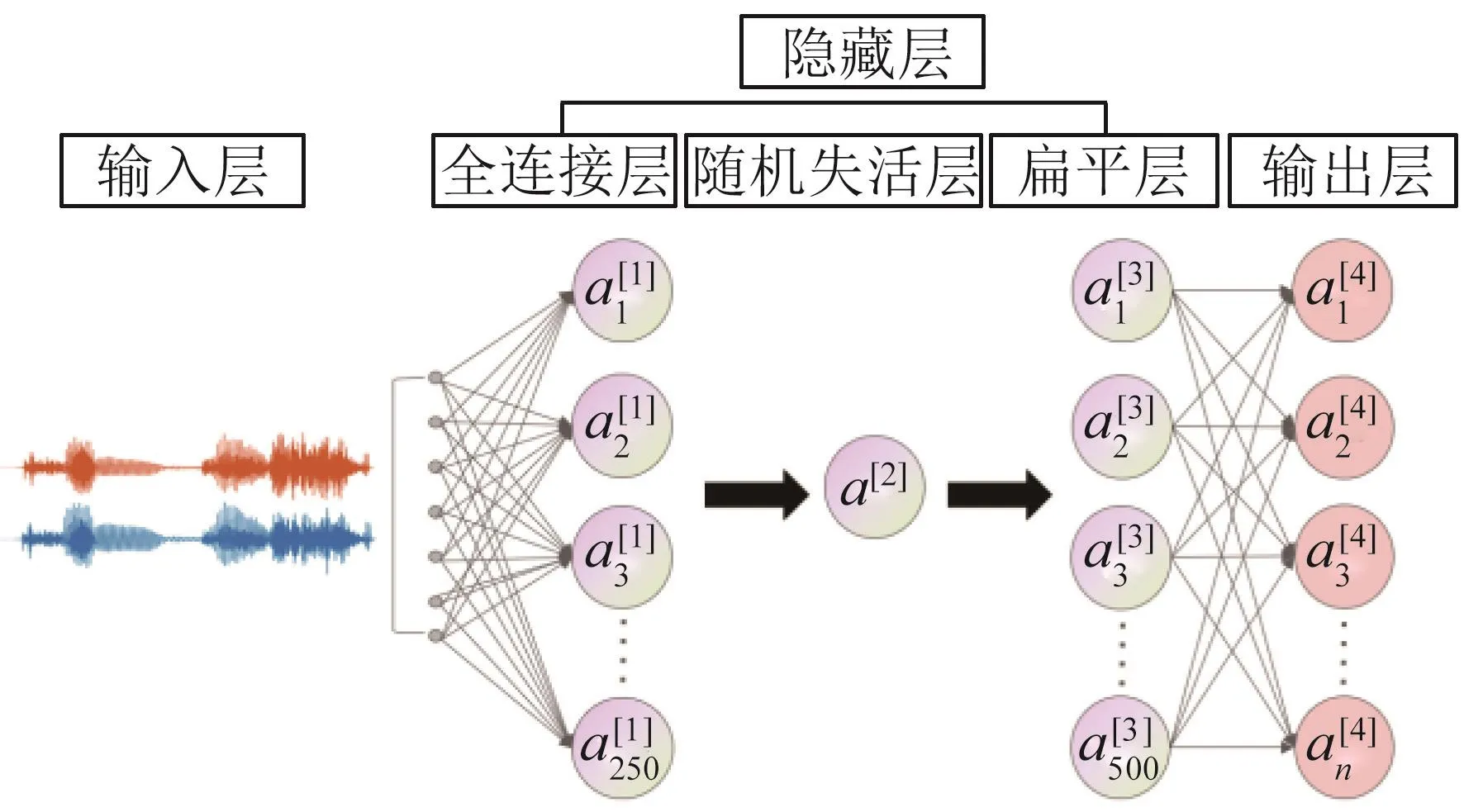
图2 深层全连接后向传播神经网络结构图Fig.2 The structure of D-BPNN

输入信号首先进入一个含250个神经元的全连接层a[1]，随后经过丢弃概率为0.3的随机失活层a[2]，最后经过扁平层a[3]后进入输出层a[4]输出，图2中输出层神经元个数n取决于所需分类的空间方位数目(见表1)。其中，第一个全连接层的激活函数为线性整流函数(Rectified Linear Units,ReLU)。与其他激活函数相比，ReLU激活函数具有提升网络训练速度、防止梯度消失及增加网络非线性能力的优点。最后一个全连接层采用Softmax函数输出，将多个输出映射到[0，1]区间内，从而实现空间方位的多分类任务。

采用Adam优化算法并使用交叉熵损失函数进行网络训练。交叉熵损失函数定义为

其中：m代表样本数，即训练集数据的总数目；n代表输出分类数，即所需分类的空间方位数目；代表第k个样本预测为第n个分类的概率。

1.3 基于CNN模型的双耳声源定位算法

CNN模型主要由三个卷积层和四个全连接层组成，网络结构如图3所示。需要说明的是，卷积层中的滤波器皆以一维卷积的形式在两个输入通道上分别做卷积，同时所有激活函数均为ReLU函数。此外，在激活函数层、卷积层、全连接层之间都加入归一化层，实现了在神经网络层的中间进行预处理的操作。

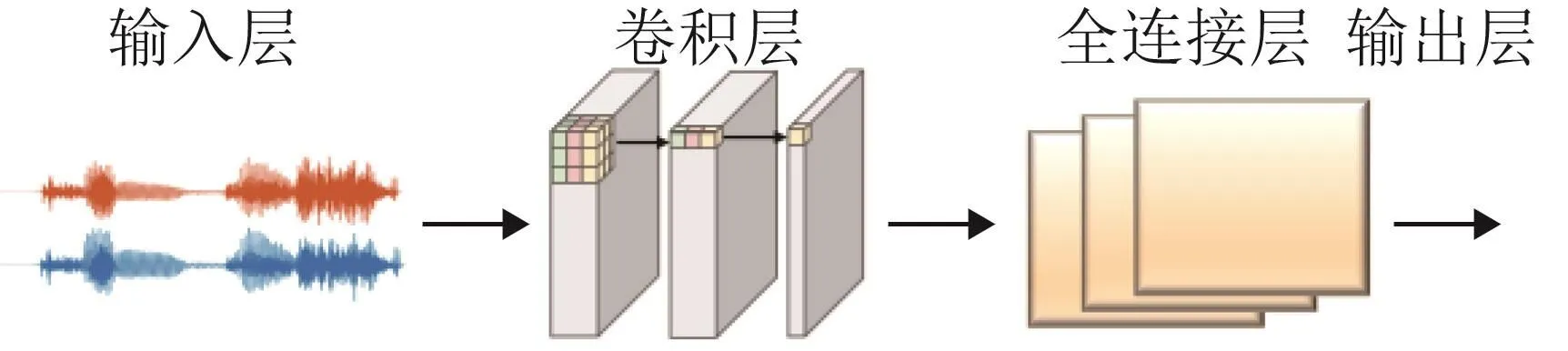
图3 卷积神经网络结构图Fig.3 The structure of Convolutional Neural Network

输入信号首先经过连续三个卷积层进行特征提取。其中第一个卷积层共有128个滤波器(卷积核)，维度为1×300，步长为30；第二个卷积层共有128个滤波器，卷积核的大小为1×40，步长为2；第三个卷积层共有64个滤波器，卷积核的大小为1×20，步长为2。输入信号经过三个卷积层后，将特征向量再输入四个全连接层。其中，前三个全连接层的神经元个数分别为2 048、1 024、128，最后一个全连接层为输出层，其神经元个数取决于所需分类的空间方位数目(见表1)。最后采用Softmax函数计算出输入数据属于每个类别的概率值，并选取概率值最大的类别作为预测方位。

此外，为了在训练时抑制过拟合，提高网络的泛化能力，全连接层中均使用Dropout方法；同时，网络在训练时采用Adam优化算法与交叉熵损失函数。

CNN模型仿真算法采用PyTorch框架实现。PyTorch框架是目前最为流行的深度学习框架之一，基于Torch框架，广泛用于自然语言处理等领域，拥有极强的易用性与灵活性。D-BPNN模型仿真算法采用Keras框架实现。Keras框架是一种高层神经网络应用程序编程接口，使用TensorFlow、Theano及CNTK作为后端，具有拓展性强的优点。上述两种模型的仿真实验均采用相同的数据集以及硬件仿真环境。硬件环境包括：Intel(R)Core(TM)i7-10750H CPU@2.60GHz 2.59GHz处理器以及NVIDIAQuadro T2000显卡。

一共进行了6组仿真实验，即2种算法模型(DBPNN模型和CNN模型)，每种执行3种空间角度间隔(15°、30°和45°)。对D-BPNN模型和CNN模型分别进行了50次和20次迭代训练后，观察到模型训练准确率达到稳定或围绕某一中值上下轻微波动，此时判定网络训练成功。图4是D-BPNN模型训练准确率随迭代次数的变化。由图4中可知，对于任何一种空间角度间隔的输入，经过50次迭代训练后训练准确率都趋于平稳；此时，3种空间角度间隔(15°、30°和45°)的训练准确率分别达到73.59%、77.18%、81.76%。

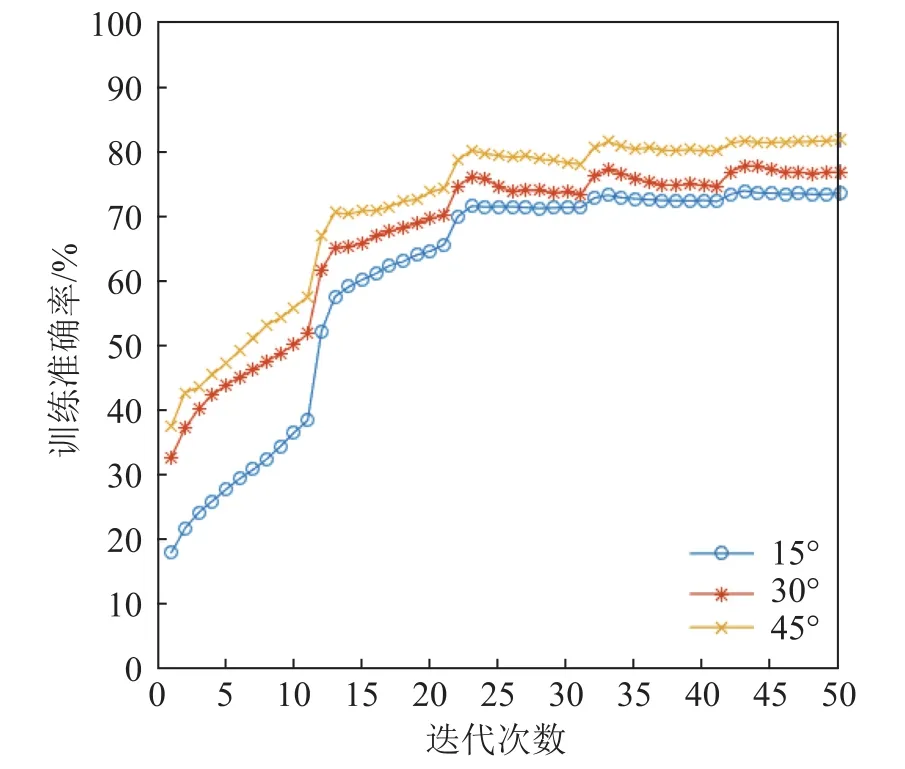
图4 深层全连接后向传播神经网络的训练准确率Fig.4 Training accuracy of D-BPNN

图5是CNN模型训练准确率随迭代次数的变化。图5中可见，对于任何一种空间角度间隔的输入，经过20次迭代训练后训练准确率都趋于平稳；此时，3种空间角度间隔(15°、30°和45°)的训练准确率分别达到96.07%、98.22%、98.93%。

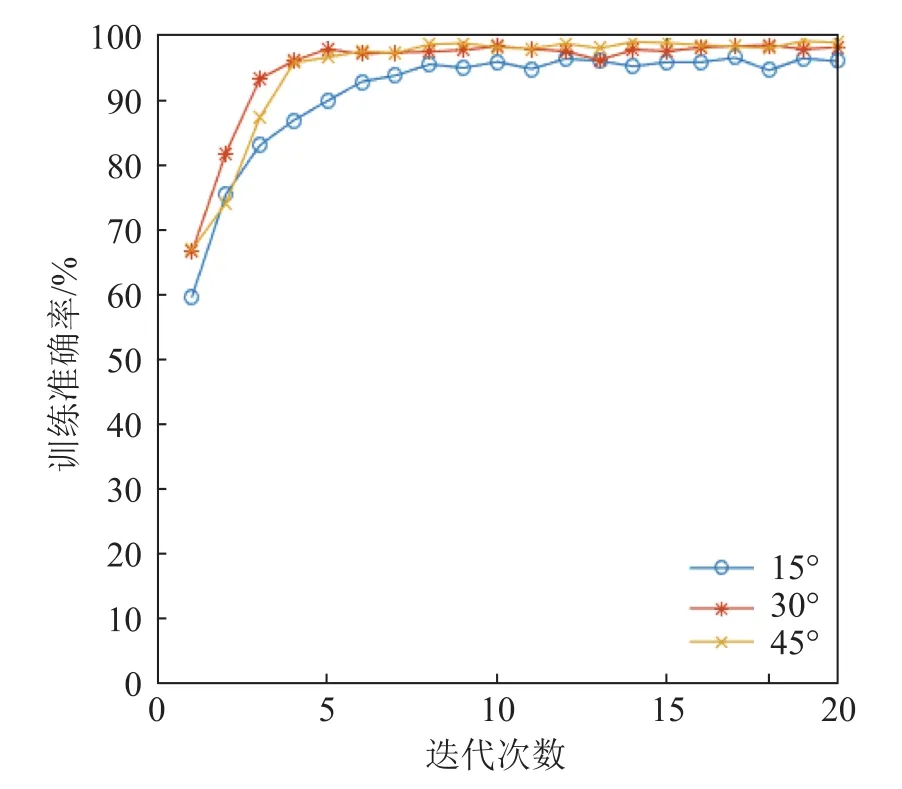
图5 卷积神经网络的训练准确率Fig.5 Training accuracy of CNN

2 实验结果和讨论

如表1所示，当网络输入的空间角度间隔为15°、30°和45°时，测试信号分别为19 031、9 133和6 174个。

2.1 模型定位效果

在人类听觉中，由于前后镜像方位(例如方位角θ=30°和θ'=150°)具有相似的ITD和ILD，因此容易出现前后混淆现象，即处于θ=30°的声源被感知处于θ'=150°，反之亦然。在听觉定位主观实验中，如果被试出现了前后混淆现象，通常是先校正混淆，即将发生混淆的方位进行空间的镜像反演，然后再进行定位准确率计算[20]。假设某个空间方位角θ共有N个测试信号，经模型预测后，有X1个测试信号的空间方位角预测为θ，即方位角预测正确；有X2个测试样本的空间方位角预测为θ'(θ与θ'互为镜像方位)，即出现前后混乱。那么，方向θ的前后混乱率R和定位准确率P分别为

在每一组实验条件下，对所有测试方位的前后混乱率和定位准确率取平均，得到该实验条件下的平均前后混乱率和平均定位准确率，如表2所示。可以看出CNN模型的平均前后混乱率远低于D-BPNN模型，其中前者的前后混乱率均低于2.24%。这表明，对于前后镜像方位，当耳间差异(ITD和ILD)无法为定位提供有效信息时，CNN模型比D-BPNN模型能更好地通过自学习提取单耳谱特征，从而可以更好地区分前后镜像方位。

为测试不同信噪比情况下的定位效果，在1.1节中生成的双耳信号中加入不同信噪比的高斯白噪声。合成的双耳带噪信号的信噪比分别为0 dB、10 dB、20 dB，分别采用CNN模型和D-BPNN模型进行方位角预测。结果表明，CNN模型的定位准确率分别为34.68%、76.92%、97.36%；而D-BPNN模型的定位准确率分别为32.85%、66.29%、85.71%。可见，在训练与测试环境不匹配的情况下，两种模型的预测准确率均有下降，但是CNN模型的鲁棒性优于D-BPNN模型。

2.2 模型训练用时

为了进一步进行模型比对，在相同实验环境下对模型的训练时长进行了测算，结果如表2所示。由表2中可见，无论是D-BPNN模型还是CNN模型，随着输入空间角度间隔的减小，训练时长都呈现上升趋势；对于相同的空间角度间隔，CNN模型的训练时长高于D-BPNN模型。进一步的计算结果表明，两者训练时长的差异随着空间角度间隔的减小而增大，例如随着空间角度间隔从45°变为15°，CNN模型训练时长高于D-BPNN模型时长的比例从7.34%增加到33.36%。

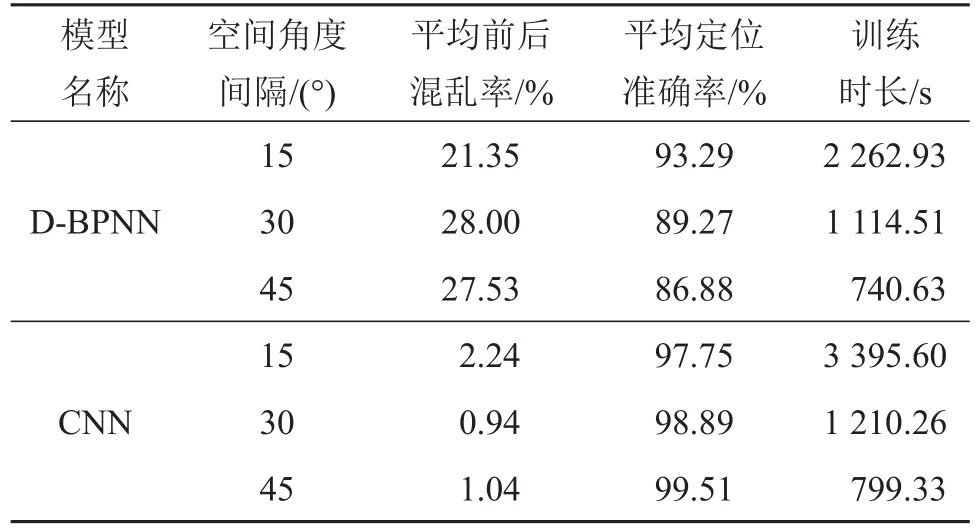
表2 基于D-BPNN和CNN的双耳声源定位算法的结果Table 2 Results of D-BPNN and CNN based binaural localization algorithms

2.3 CNN模型滤波器的分析

通过前后混乱率和定位准确率指标的对比研究发现，在同等实验条件下CNN模型的预测效果优于D-BPNN模型。为了进一步探究这一现象的内部机制，对空间角度间隔为15°的输入信号CNN模型中的三个卷积层的典型滤波器进行了展示，如图6所示。限于篇幅，各层中仅选取一个典型滤波器进行分析。

滤波器代表CNN模型中对应卷积核的参数权重，用于提取相应的深度神经网络内部特征。在训练效果良好的模型中，滤波器图形往往展现出平滑的滤波特性；卷积核的参数权重在第一个卷积层中体现出可解释性，但是这种可解释性随着层次的加深而逐渐消失。

图6(a)中显示出类似于语音信号的波形，这是CNN模型对输入信号进行特征提取的过程，展现了第一个卷积层对其卷积核参数权重的可解释性。这类似于双耳听觉定位时，人类的神经系统自动根据双耳接收信号对各类参数差异进行判断。图6(b)、6(c)分别为第二层、第三层的典型滤波器的结果。与图6(a)相比，图6(b)的特征趋于抽象，主要表现为密集的波动。图6(c)的特征则是在图6(b)特征上的进一步提取和抽象，主要表现为平缓的波动。可见，随着网络卷积层次的加深，更加抽象、基本的类别信息将被抽取；同时，对卷积核参数权重的可解释性也逐渐降低。

图6 卷积神经网络的典型滤波器Fig.6 Typical filters in CNN

3 结论

本文针对多种双耳定位因素存在复杂关联的问题，提出了两种基于深度学习的算法模型：深层全连接后向传播神经网络D-BPNN模型和卷积神经网络CNN模型；并采用前后混乱率、定位准确率、训练时长等指标，比较了两种深度学习模型在不同空间角度间隔情况下的仿真效果。

实验结果表明：随着输入信号的空间角度间隔的减小，D-BPNN模型的定位准确率逐渐递增；而CNN模型的定位准确率趋于稳定，达到98%左右。当D-BPNN或CNN训练信号空间角度间隔减小时，训练时长呈现上升趋势；同一空间角度间隔时，CNN模型的训练时长均高于D-BPNN模型；随着水平面空间角度间隔从45°变为15°，CNN模型时长高于D-BPNN模型时长的比例从7.34%增加到33.36%。

综上所述，在相同的实验条件下，虽然卷积神经网络在对双耳听觉声源定位算法中比BP神经网络需要耗费相对更多的训练时长，但其拥有更高的定位准确率、更强的泛化能力与更低的前后混乱率。实际应用时，可根据用时和精度的具体需求进行算法选择。