水声通信多通道最大似然联合均衡译码方法

胡承昊，王海斌，台玉朋，汪 俊

(1.中国科学院声学研究所，声场声信息国家重点实验室，北京 100190；2.中国科学院大学，北京 100049)

0 引言

水声信道多途时延扩展长，且存在复杂的时空变化，由此导致的码间串扰(Intersymbol Interference,ISI)严重限制了水声通信系统性能[1]，因此，需要设计高性能的均衡方法抵抗水声信道ISI。此外，远距离水声通信信号衰减严重，需要利用阵列接收以提高信号增益。垂直阵是一种常用的阵列形式，然而，由于水下声传播的固有特性，声场垂向分布存在明显差异，当采用垂直阵接收时，不同深度处接收信号相关性较低[2]。此时，采用传统阵列信号处理方法难以获得理想的空间增益。

为了在垂直阵接收情况下获取空间增益，Milica等于1993年提出了一种水声通信多通道判决反馈均衡方法(Multichannel Decision Feedback Equalizer,M-DFE)[3]，该方法将各通道接收信号分别经过一个前馈滤波器，抵消部分水声信道的ISI，随后将各通道前馈滤波器的输出合并，并先后经过判决器和反馈滤波器反馈至合并器，从而减少由已判决接收符号造成的ISI。此后，学者们针对该方法展开了大量研究。文献[4-5]利用快速优化最小均方误差算法减小了自适应更新步长对算法结果的影响。文献[6-7]分别从理论和实验的角度分析了滤波器阶数、联合通道数等因素对均衡结果的影响。文献[8]对比分析了采用不同自适应算法时M-DFE方法的均衡性能。此外，基于时间反转的多通道判决反馈均衡方法(Time Reversal Decision Feedback Equalizer,TR-DFE)也得到了广泛研究[9-11]，此类方法在牺牲部分均衡效果的同时，能够达到比MDFE方法更低的算法复杂度，并且能够有效降低算法对译码参数的敏感程度[12]。目前，M-DFE方法仍然是水声通信常用的一类多通道接收处理方法。然而，此类方法将均衡后的各通道信号直接叠加，采用这种方式，各通道的残留多途干扰以及环境噪声会造成通道间干扰，影响通信性能。多年来，这一问题始终没有得到有效解决，是该方向的重要难点。

近年来，将信道译码和信道均衡相结合的联合均衡译码方法成为了水声通信研究的热点。2016年，台玉朋等[13-14]提出了一种水声通信联合均衡译码方法，在线性复杂度下实现了信道均衡与信道译码的联合优化，取得了较优的均衡译码性能。该方法的提出也为在联合均衡译码过程中一体化融合空间多通道接收信息提供了解决思路。

本文提出了一种水声通信多通道最大似然联合均衡译码方法(Multichannel Joint Equalization and Decoding,M-JECD)，按照最大似然准则，在一体化的联合均衡译码树中，将各通道接收信号转化为序列似然概率，并在此基础上进行信息融合而非信号叠加，有效避免了传统方法的通道间干扰，进一步提高了水声通信系统的性能。同时，本文方法在线性复杂度下实现多通道联合均衡译码，具有较高的实用价值。

1 本文方法的整体结构

图1给出了本文方法的整体结构框图。编码端长度为D的信息序列M=[m1m2…mD]经信道编码得到编码符号序列X=[x1x2…xN]。本文方法可支持多种信道编码方式，下面以Spinal码[15]为例进行说明。图2给出了Spinal码的基本原理框图。编码前，首先将待发送的信息序列等长地划分为D′个长度为g的信息片段，通过哈希函数fh递归地生成各信息片段的种子sd=fh(sd-1，md)。随后，利用各信息片段的种子sd驱动随机映射器，递归地生成一系列编码符号，编码符号经过调制发送至水声信道。

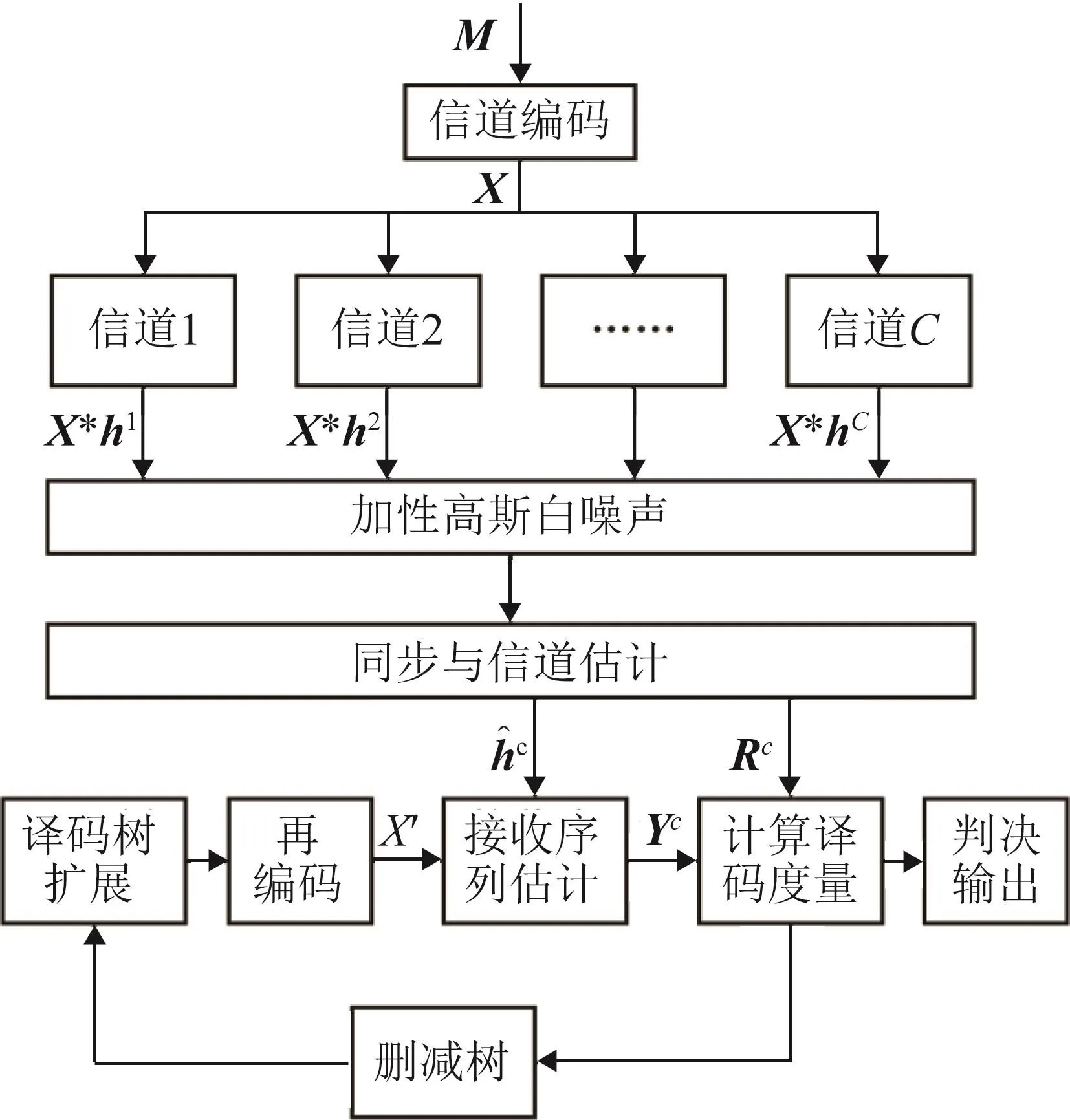
图1 本文方法的整体结构框图Fig.1 The structure of the proposed algorithm

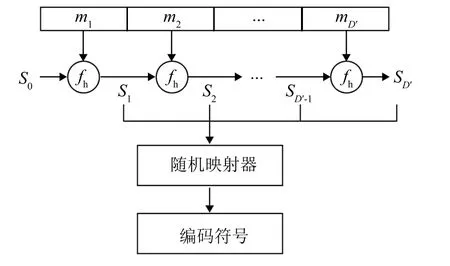
图2 Spinal码的编码原理Fig.2 The coding process of Spinal codes

接收端采用空间中不同位置的C个接收器接收水声信号。各通道分别进行同步和解调，获得接收符号序列Rc=X*hc+Wc，其中，Rc为通道c的接收符号序列，hc为通道c对应的信道冲激响应，*表示卷积，是均值为0、方差为σ2c的高斯白噪声。多通道最大似然联合均衡译码器根据各通道的接收符号序列Rc和信道冲激响应估计结果对发送信息序列进行估计，输出译码结果

2 多通道最大似然联合均衡译码方法

将译码看作一个序列估计过程，采用最大似然准则进行译码，则译码结果可表示为

其中：X(M′)为发送信息序列M′时的编码符号序列。根据编码符号序列和各通道信道冲激响应hc，对各通道期望接收符号序列进行估计，可得Yc=X(M′)*hc。假设各通道接收的环境噪声不存在相关性，则序列似然概率可表示为

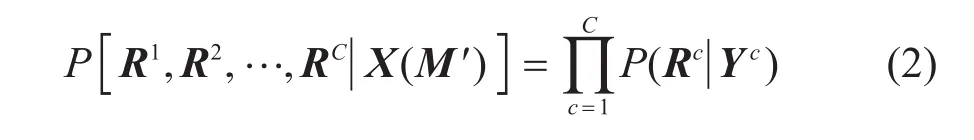
由于各通道接收符号序列与发送符号序列之间存在Rc=X*hc+Wc的关系，因此，当环境噪声满足方差为的高斯分布时，利用各通道接收信号可分别计算与之对应的序列似然概率：

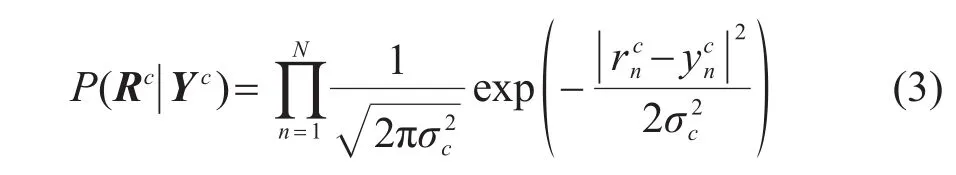
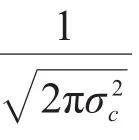
由式(5)可知，在本文方法的均衡译码过程中，各通道的接收信号并非直接叠加，而是根据信道和编码结构，在译码端转换为似然概率，并在一体化的均衡译码树上进行融合，得到统一的译码度量。因此，与M-DFE方法相比，本文方法可有效避免通道间干扰，进一步提高水声通信性能。

理想情况下，译码器搜索所有可能的信息序列，最终选择译码度量最大的序列作为译码结果。为了高效、有序地计算各信息序列的译码度量，本文采用基于译码树的方式实现多通道最大似然联合均衡译码。从收发端约定的根节点出发，逐信息片段地构建译码树。假设Spinal编码过程中各信息片段的长度为gbit，则由译码树中每个节点均可扩展出2g条分支，分别对应信息片段的每种可能取值。如果节点B由节点A扩展得到，则称节点A为节点B的母节点。

译码树每向下扩展一次，便称其扩展了一层。对于译码树中的每条分支，采用与编码端相同的方式再现编码过程，得到与之对应的编码符号序列X′=[x′1x′2… x′Nd]，其中，Nd为第d层译码树对应的接收符号数量。利用各通道的信道估计结果和载波相位估计结果可分别得到各通道期望接收符号序列的估计值：

其中：La和Lc分别为信道冲激响应估计结果中非因果成分和因果成分的抽头数量；为中的第 l个分量；为通道c的载波相位估计结果。根据式(5)将各通道的接收信息相融合，可得各节点的译码度量为

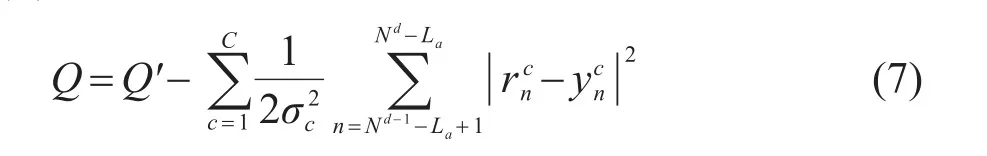
其中：Q′为各译码节点母节点的译码度量。

为了跟踪水声信道和载波相位的时变性，在译码过程中分别采用式(8)、(9)对各通道的信道冲激响应和载波相位估计结果进行自适应更新：

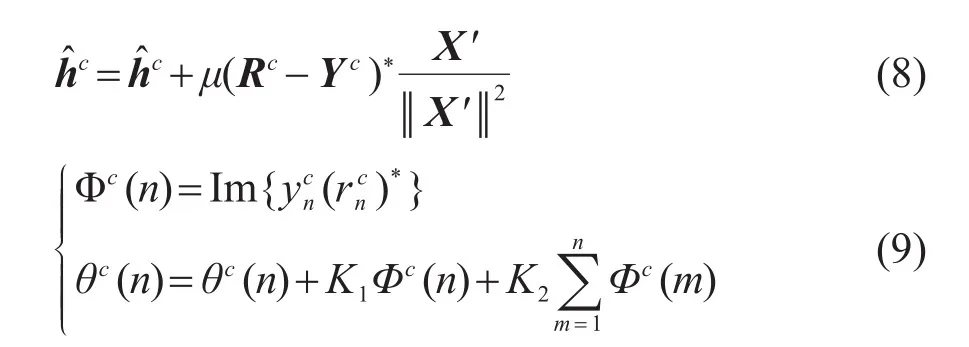
其中：μ、K1和K2为预设的自适应更新步长；Φc(n)为n时刻通道c的鉴相器等效输出；(A)*表示A的共轭；Im{·}表示取复数的虚部。

为了降低算法复杂度，本文采用删减树算法来减小译码树规模。在译码过程中，对每层译码树均保留译码度量最大的B条路径继续向下扩展，其余路径则被删除。如此，本文方法的复杂度得到有效降低，仅为O(CBD2g)，复杂度随码长和联合通道数线性增长，具有较高的实用价值。

3 仿真分析

为了分析本文方法对水声通信系统性能的提升效果，分别对本文方法和M-DFE方法的误码率性能进行仿真分析。仿真过程中，令Spinal编码中每个信息片段的长度g=1bit，采用64-PSK调制生成通信信号并发送至水声信道。仿真发送符号速率为每秒150个，通信速率为150 bit·s-1。在发送信号前，加入长度为1 000个符号的训练序列，用于MDFE方法的滤波器训练和本文方法的信道估计。采用3个通道进行接收，每个通道均对应一个实测时变水声信道，通道1～3对应的信道冲激响应h1、h2和h3分别如图3(a)、3(b)、3(c)所示。仿真所用信道提取自2019年在千岛湖水域实测的水声通信信号，实验水域水深约为45 m，发射信号中心频率为7.5 kHz，带宽为5 kHz。仿真过程中，令译码树宽度B=1 024。

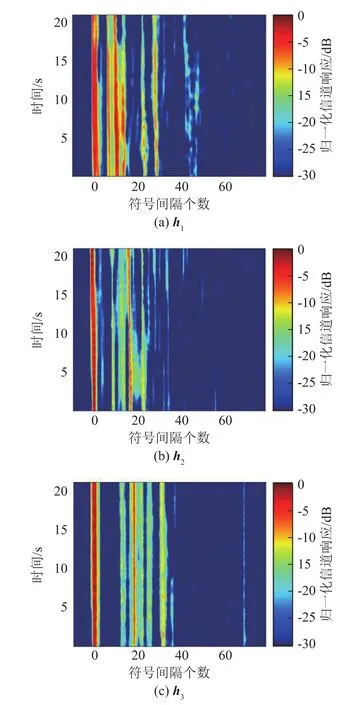
图3 仿真所用时变信道冲激响应Fig.3 The time-varying channel response used in simulation

3.1 单通道与多通道条件下本文方法的误码率性能分析

首先对单通道和联合多通道时本文方法的误码率性能进行分析，图4给出了不同信噪比下的误码率，图中同时给出了加性高斯白噪声(Additive White Gaussian Noise,AWGN)信道下的仿真结果，并以此作为本文方法的性能极限。由图4可知，在AWGN信道下，误码率同样达到10-3，本文方法利用单通道译码时所需最低信噪比为2.76 dB，而联合3通道时为-1.39 dB，与之相比可获得约4.15 dB的信噪比增益。而在时变水声信道下，误码率同样达到10-3，本文方法在利用通道1～3译码时所需最低信噪比分别为7.6、6.1和6.1 dB，而联合3通道时为0.8 dB，与单通道相比可分别获得约6.8、5.3和5.3 dB的信噪比增益。本文方法在一体化的均衡译码树中实现了多通道信息融合，能够在获取空间增益的同时利用多通道信息提高均衡和译码的性能，从而获得比AWGN信道下更高的信噪比增益。

图4 利用单通道和联合3通道时本文方法的误码率Fig.4 The bit error rates of the proposed algorithm when using a single channel and the combined 3 channels

3.2 本方法与M-DFE方法的误码率性能分析

接下来，在各通道接收信噪比相等的条件下，对本文方法与M-DFE方法的误码率性能进行分析，图5给出了两种方法的误码率仿真结果。由图5可知，误码率同样达到10-3所需的最低输入信噪比，M-DFE方法为2.0 dB，而本文方法为0.8 dB，与之相比可获得约1.2 dB的信噪比增益。

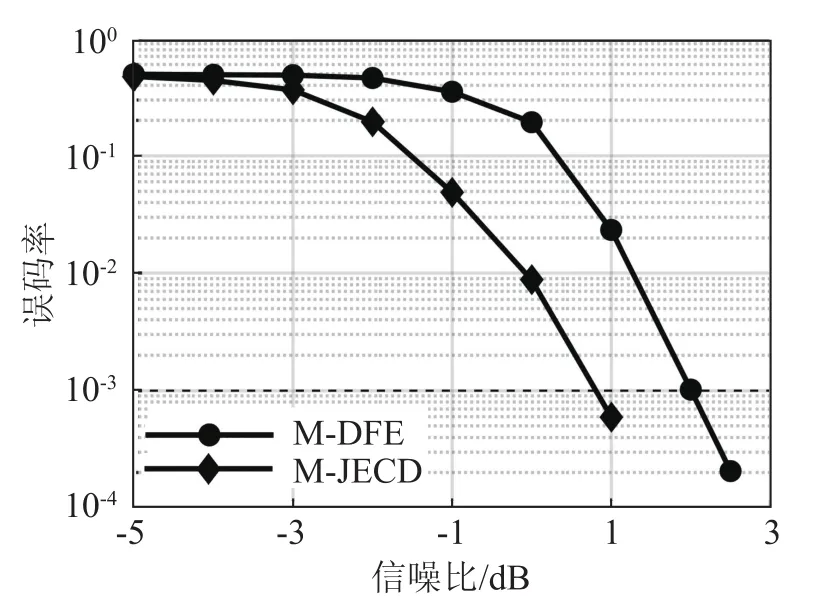
图5 各通道接收信噪比相等时本文方法与M-DFE方法的误码率Fig.5 The bit error rates of the proposed algorithm and MDFE algorithm when the SNR of each channel is equal

由于水下声传播的固有规律，一般情况下，不同深度的声信号能量和环境噪声均存在差异，导致各通道接收信噪比并不相等。因此，本文对各通道接收信噪比存在差异时，本文方法和M-DFE方法的误码率性能进行仿真，结果如图6所示。仿真过程中，令通道1和通道3的接收信噪比相比通道2分别提高和下降3 dB。图6中横轴表示通道2的接收信噪比。

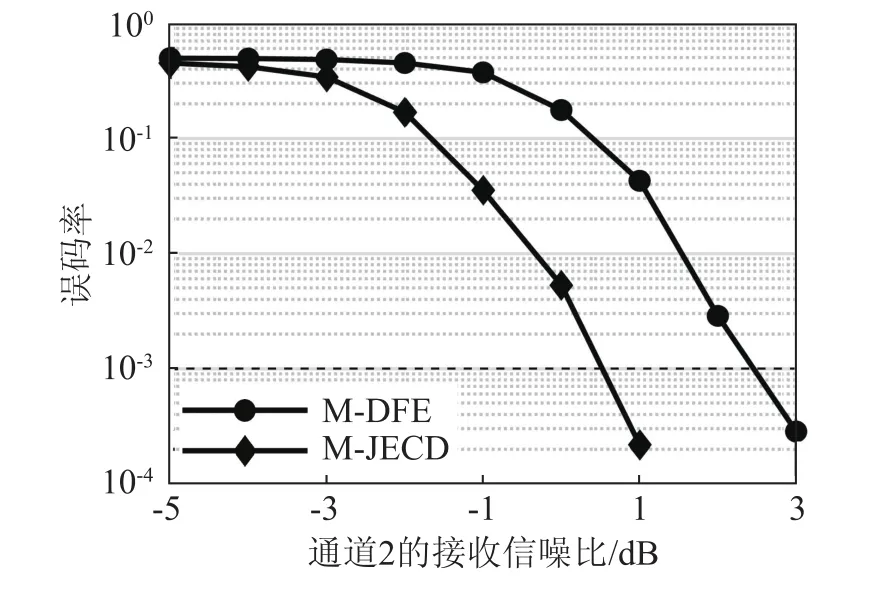
图6 各通道信噪比存在差异时本文方法与M-DFE方法的误码率Fig.6 The bit error rates of the proposed algorithm and M-DFE algorithm when the SNR of each channel is different

由仿真结果可见，当各通道接收信噪比存在差异时，本文方法可将系统误码率达到10-3所需信噪比由M-DFE方法的2.5 dB降低至0.5 dB，与之相比可获得约2 dB的信噪比增益。此时，各通道信噪比的差异放大了传统M-DFE方法通道间干扰的影响，导致通信性能下降。而本文方法通过在一体化均衡译码树上实现多通道信息融合，受各通道接收信噪比差异的影响更小，在这种情况下可以取得更大的性能优势。

4 海上实验

4.1 实验概况

为验证本方法在真实水声通信中的性能，2019年4月，在西太平洋海域开展了一次深海水声通信实验，图7为实验的布设示意图。实验海区平均海深约为5 512 m。发射船在多个预设站位发射不同速率的通信信号，其中，站位T1的通信距离为83.2 km，站位T2的通信距离为40.9 km。发射时，声源平均深度约为106 m，发射声源级约为186 dB。接收端采用垂直水听器阵列接收信号。

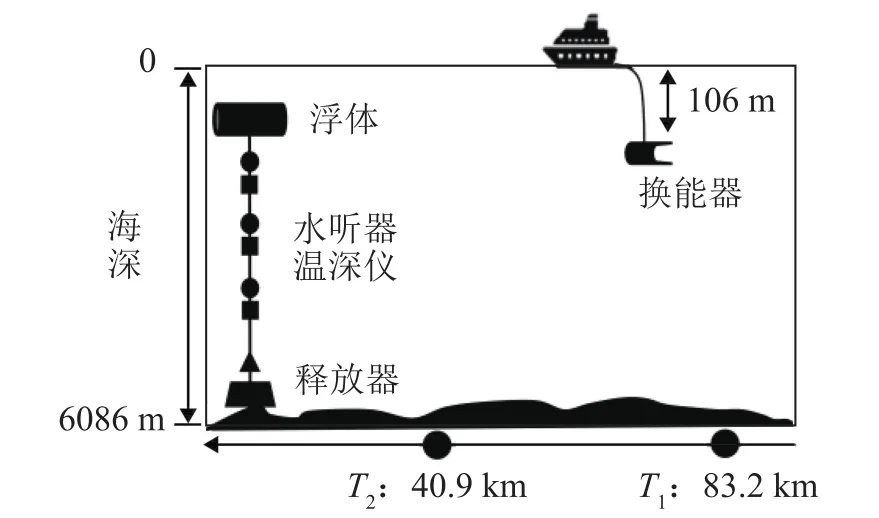
图7 海上实验布设示意图Fig.7 Layout of the sea trial

本次实验同时对不同距离的传播损失进行了测量，图8给出了三个通道的测量结果，其中，通道1、通道2和通道3的接收深度分别为241、381和511 m。由图可见，第一个发射站位处在第二声影区，第二个发射站位处在第一声影区。

图8 通道1,2,3中的实测传播损失Fig.8 The measured transmission losses in Channel1,2 and 3

编码时，令各信息片段的长度g=1，采用32-PSK调制，发送符号速率为每秒150个。本次实验发送信号的最高通信速率为450 bit·s-1，最低为15 bit·s-1。

4.2 实验结果

首先对站位T1的实验信号进行分析，图9分别给出了3个接收通道对应的时变信道冲激响应估计结果和瞬时信道冲激响应估计结果。各通道的平均接收信噪比分别为-4.3、-6.4和-8.2 dB。可见，该站位接收信号对应的信道时延扩展较短，接收信噪比较低。

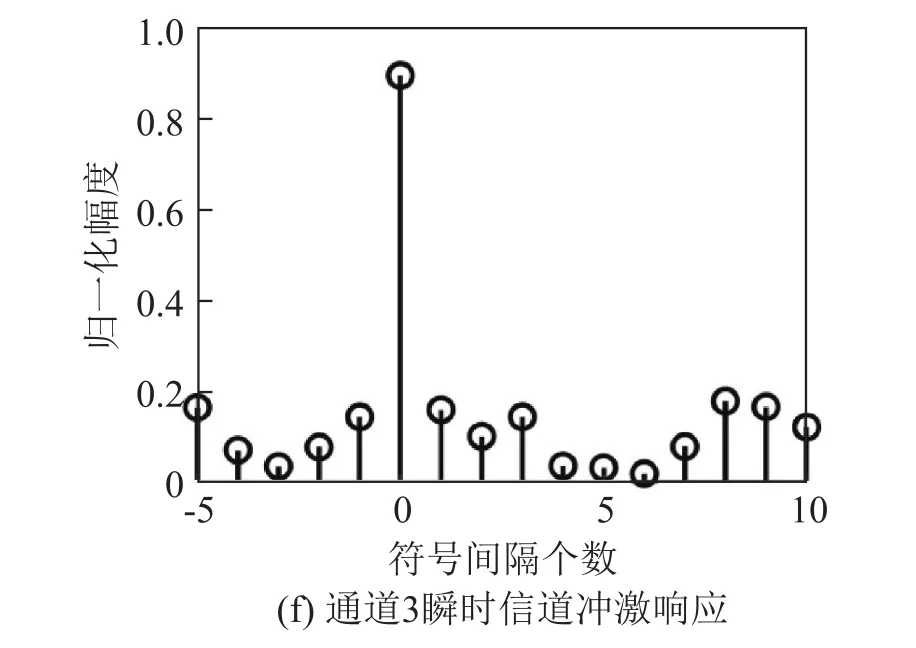
图9 各通道站位T1实测的时变信道冲激响应和瞬时信道冲激响应Fig.9 The time-varying channel responses and the instantaneous channel responses measured at Station T1in each channel

分别利用本文方法和M-DFE方法进行译码，统计该信号在不同通信速率下的误码率，结果如图10所示。译码过程中，令译码树宽度B=4 096。由图10可见，对于通信速率为112.5 bit·s-1的通信信号，采用本文方法可以实现正确译码，而此时M-DFE方法的误码率为7.3×10-2。对于通信速率为90 bit·s-1的通信信号，M-DFE方法能够实现正确译码。此时，本文方法实现正确译码的通信速率为M-DFE方法的1.25倍。

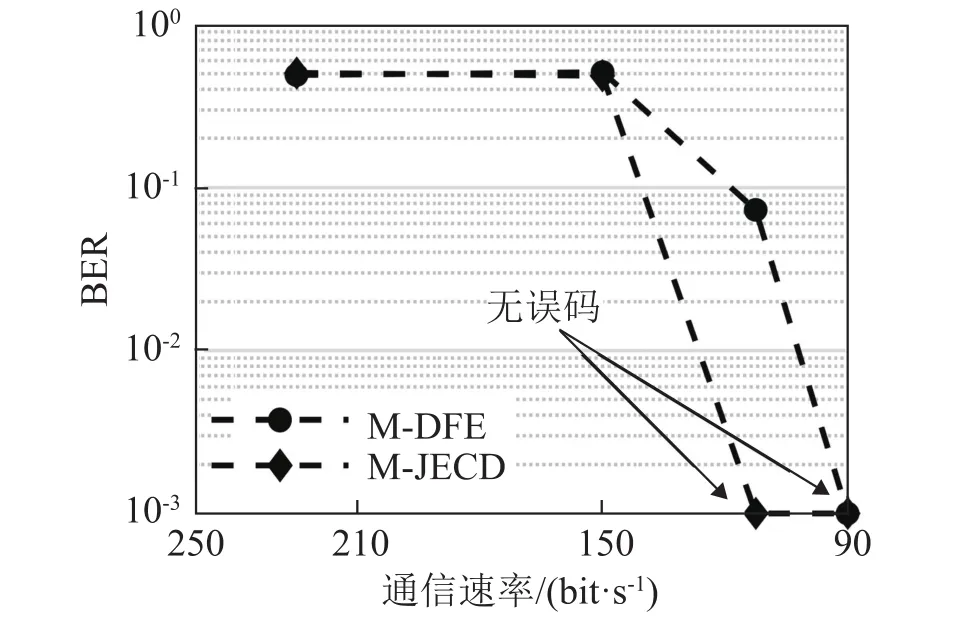
图10 站位T1实测的本文方法和M-DFE方法在不同通信速率下的误码率Fig.10 Bit error rates of the proposed algorithm and the MDFE algorithm under different communication rates measured at Station T1

接下来，对站位T2的实验信号进行分析，图11分别给出了3个接收通道对应的时变信道冲激响应估计结果和瞬时信道冲激响应估计结果。各通道的平均接收信噪比分别为-3.3、-5.5和-7.1 dB。由图11可见，通道1对应的信道冲激响应时延扩展约为60个符号间隔，而通道2和通道3对应的信道冲激响应时延扩展则可达80个符号间隔以上。

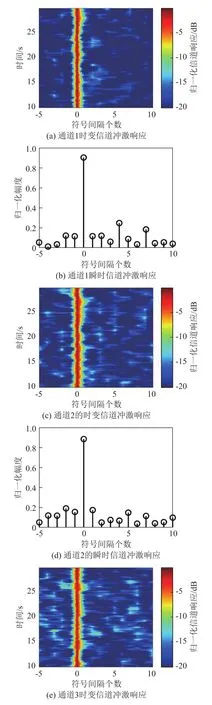
图11 各通道站位T2实测的时变信道冲激响应和瞬时信道冲激响应Fig.11 The time-varying channel responses and instantaneous channel responses measured at Station T2in each channel

分别利用本文方法和M-DFE方法进行译码，统计不同通信速率下的误码率，结果如图12所示。译码过程中，令译码树宽度B=4 096。由图12可见，对于通信速率为37.5 bit·s-1的通信信号，采用本文方法可实现正确译码。然而即使是通信速率最低的15 bit·s-1通信信号，M-DFE方法仍然无法实现正确译码。可见，在这种信道较为复杂、接收信噪比低且各通道接收信噪比存在差异的情况下，MDFE方法的性能大幅下降，而本文方法仍然能够达到较优的均衡译码性能。

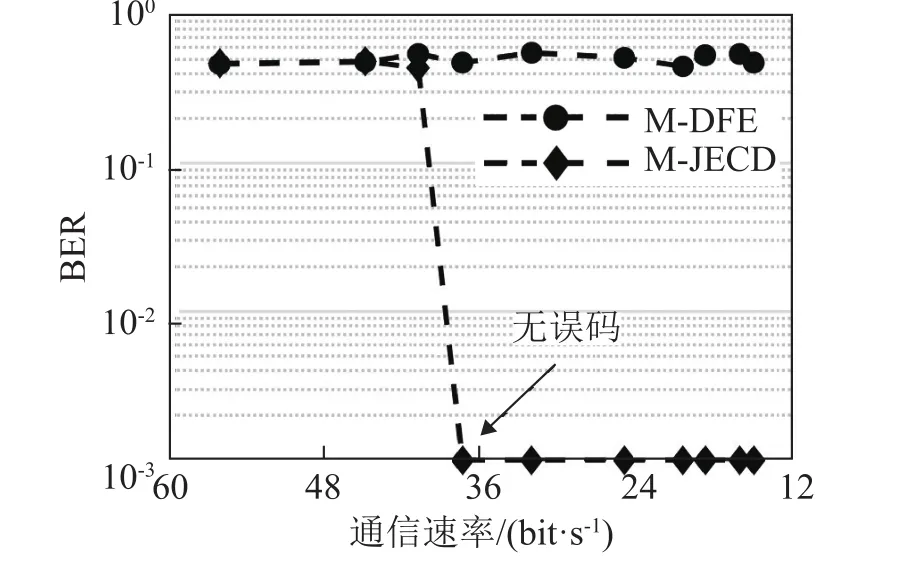
图12 站位T2实测的本方法和M-DFE方法在不同通信速率下的误码率Fig.12 Bit error rates of the proposed algorithm and the MDFE algorithm under different communication rates measured at Station T2

5 结论

本文提出了一种水声通信多通道最大似然联合均衡译码方法。该方法在一体化的均衡译码树中同时进行信道译码和最大似然均衡，将各通道接收信号转换为序列似然概率，并在此基础上实现多通道信息融合，能够有效避免传统M-DFE方法中的通道间干扰，从而进一步提高水声通信性能。同时，本文方法采用删减树算法以减小译码树规模，使算法复杂度随码长和联合通道数呈线性增长，具有较高的实用价值。

仿真结果表明，本文方法能够取得比M-DFE方法更低的误码率，并且当各通道的接收信噪比存在差异时，本文方法能够取得更大的性能优势。海上实验结果表明，对于发射站位T1的实验信号，M-DFE方法实现正确译码的通信速率为90 bit·s-1，而本文方法为112.5 bit·s-1，是M-DFE方法的1.25倍。对于发射站位T2的实验信号，本文方法实现正确译码的通信速率为37.5 bit·s-1，而M-DFE方法对于通信速率最低的15 bit·s-1通信信号仍然无法实现正确译码。