阵元失效对克罗内克积波束形成性能的影响
2022-10-17戴金洲孟维鑫郑成诗
戴金洲,沙 硕,厉 剑,孟维鑫,郑成诗
(1.北京市计量检测科学研究院,北京 100029;2.中国科学院大学,北京 100049;3.中国科学院声学研究所,北京 100190)
0 引言
基于传声器阵列的波束形成技术可以构建空间滤波器定向提取目标信号并抑制干扰[1]。波束形成技术按照数据相关性划分,可分为固定波束形成器和自适应波束形成器。固定波束形成器包括延迟求和波束形成器、超指向性波束形成器等,其运算复杂度低,但噪声抑制能力有限;自适应波束形成器包括最小方差无失真响应(Minimum Variance Distortionless Response,MVDR)波束形成器[2-5]、广义旁瓣消除器(Generalized Sidelobe Cancellation,GSC)[6-8]、多通道维纳滤波(Multi-channel Wiener Filtering,MWF)等[9-11],这类波束形成器可以根据噪声信号的变化自适应地抑制干扰噪声,具有较强的方向性干扰噪声抑制能力。然而,自适应波束形成器也存在以下问题:首先,自适应波束形成器需要对信号协方差矩阵进行求逆运算,为避免奇异,当传声器阵元数较多时往往需要更多的快拍数估计协方差矩阵,且矩阵求逆运算复杂度迅速增加,导致波束形成鲁棒性降低而系统复杂度增大;其次,自适应波束形成器对导向矢量误差和协方差矩阵误差都较为敏感,这两种误差会造成波束形成器性能大幅下降[4]。因此,如何利用较少的快拍数设计鲁棒的波束形成器一直是该方向的研究热点。
对于一类规则阵型(例如均匀线阵、均匀面阵等)的传声器阵列,其导向矢量对应的高维矩阵可以分解为两个低维的虚拟矩阵的克罗内克积(Kronecker Product,KP)。Benesty等[12-14]将这一特性应用于传声器阵列,提出了KP波束形成器,并推导了线阵和面阵的KP波束形成器的解析式。Rajib等[14]分析了KP混合波束形成器应用于远场语音信号时的收敛性和鲁棒性。研究结果表明,基于KP分解的MVDR波束形成器(KP-MVDR)可以在保证降噪效果的前提下,显著提高波束形成方法的鲁棒性,同时降低计算复杂度。该方法可以提高波束形成的鲁棒性,主要是将KP-MVDR的权向量分解为两个虚拟子阵列的MVDR权向量的克罗内克积的形式,相当于将传声器阵列的等效自由度降低到两个虚拟子阵中阵元最大数,从而提高鲁棒性。
在实际工程应用中,由于传声器焊接工艺、芯片底层数据采集驱动等问题可能会导致传声器采集信号出现错误,导致传声器阵列的若干阵元失效,影响最终的波束形成结果。常见的阵元失效包括三种情况:第一种是信号幅度异常变小或为0,第二种是信号中只有自噪声,第三种是某些传声器信号完全一致。实际中可通过特征提取对比和压缩感知等方法准确地检测出异常的信号通道[15-16],从而在波束形成中仅用有效阵元采集的信号。然而,上述方法并不适用于KP-MVDR波束形成器,因为此时均匀阵列将变为非均匀阵列,其导向矢量不能够进行克罗内克分解,导致KP-MVDR波束形成算法的理论模型失配。另一方面,若直接使用失效阵元的数据可能会严重影响噪声的协方差矩阵估计,导致自适应波束形成器性能下降。为了解决上述问题,本文将分析不同阵元失效情境下各种自适应波束形成器的性能,并给出相应场景下提高自适应波束形成器性能的解决方法。本文将以鸣笛数据为例进行对比测试。仿真及实际数据实验结果表明,本文提出的改进方法可以有效提高失效阵元场景下的KPMVDR及MVDR波束形成器性能。
本文建立了信号模型,对基于均匀面阵的MVDR及KP-MVDR算法进行讨论,分析了不同阵元失效场景下的波束形成器性能,并提出了阵元失效的解决方法。
1 信号模型
如图1所示,考虑M元均匀面阵,其垂直xOy平面并位于xOz平面上,阵列中心放置在原点,每一行有M1个全指向性传声器,每一列有M2个全指向性传声器,满足M=M1M2,任意两个相邻传声器间隔为δ。阵列采集信号经过K点短时傅里叶变换(Short-time Fourier Transform,STFT)后表示为

图1 均匀面阵模型及其KP分解示意图Fig.1 Schematic diagram of uniform rectangular array model and its KP decomposition
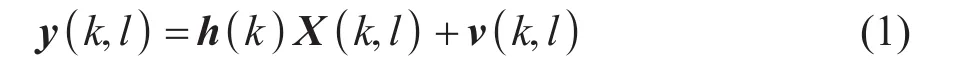
其中:y(k,l)=[Y1(k,l)...YM(k,l)]T为阵列采集信号在第l帧第k个频点对应的频谱分量,l∈ {1,2,...,L},k∈ {1,2,...,K}。X(k,l)为期望信号,v(k,l)=[V1(k,l)...VM(k,l)]T为 加 性 噪 声 矢 量 ,h(k)为目标信号导向矢量。假设目标声源距离传声器阵列较远,满足远场假设,且以角度Ω0=[φ0θ0]T入射,其中φ0和θ0分别为俯仰角和水平角,此时期望信号导向矢量可以表示为

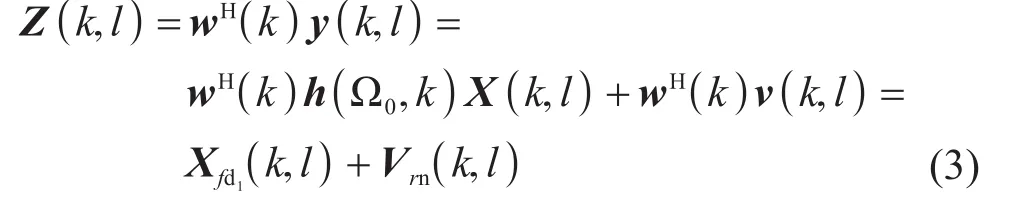
其中:Xfd1为输出的期望信号,Vrn为残留噪声成分。
2 基于克罗内克积的波束形成器
2.1 最小方差无失真响应波束形成器
最小方差无失真响应波束形成器的优化准则是在期望方向信号无失真的约束下最小化噪声能量,具体可表示为
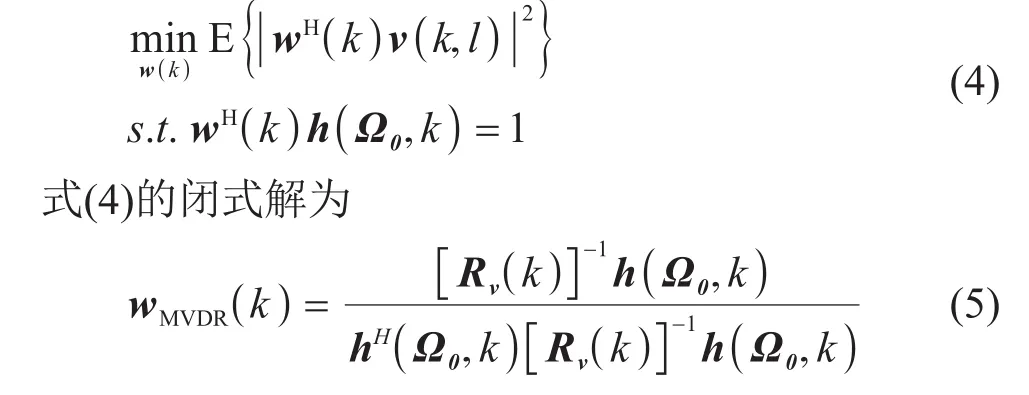
其中:Rv(k)=E{v(k,l)vH(k,l)}为干扰噪声协方差矩阵。MVDR波束形成器需要已知干扰噪声协方差矩阵,但采集信号是期望信号与加性噪声的混合信号。本文考虑车辆鸣笛声检测及提取的实际应用场景,在该场景中,鸣笛信号在时间维度上较为稀疏,而道路噪声等噪声信号几乎一直存在,可通过长时统计的方法估计干扰噪声协方差矩阵。
2.2 基于克罗内克积的最小方差无失真响应波束形成器
KP-MVDR波束形成器将整个阵列分解为两个虚拟子阵的克罗内克积形式,对每个虚拟子阵分别进行传统MVDR滤波,再将虚拟子阵对应的滤波器利用克罗内克积重构出整个阵列的空间滤波器,下面以图1所示的均匀面阵介绍KP-MVDR算法。

该优化问题为双变量优化问题,不存在闭式解,可采用文献[14]提出的迭代方式进行求解。选虚拟子阵1作为迭代初始阵列,则第n次迭代时虚拟子阵1的滤波器系数为

将其记为基于克罗尼克积的最小方差无失真响应联合延迟求和(Kronecker Product Minimum Variance Distortionless Response Delay and Sum,KP-MVDAS)波束形成器。
3 阵元失效对波束形成性能的影响
KP-MVDR波束形成器可以降低估计协方差矩阵所需的快拍数,同时降低计算复杂度,但其只能适用于一类规则阵列。如前所述,当规则阵列中出现阵元失效时,如果依然使用这些失效阵元,可能会导致KP-MVDR的性能有所下降,但该问题至今未有相关理论研究和实验研究工作。本节将以KP-MVDR波束形成器以及MVDR波束形成器为例,分析阵元失效对其波束形成性能的影响,并提出相应解决方案以提高它们的波束形成性能。
3.1 理论分析
为简化问题,假设噪声是由Ωi=[φiθi]T方向入射的干扰噪声以及传声器自噪声组成:

相应的噪声协方差矩阵为
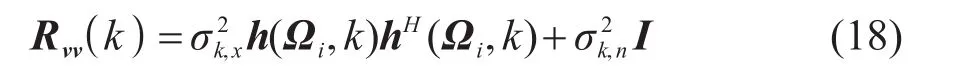
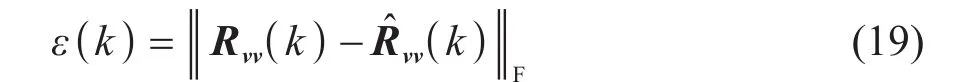
下面将针对三种不同阵元失效场景进行具体分析。
(1)阵元采集信号为0
不失一般性,面阵阵元将按照从左到右,从上到下的顺序进行排序编号,当第m个传声器采集信号为0时,实际得到的噪声协方差矩阵为


本文以窄带信号为例对上述理论分析进行仿真验证。仿真测试选用阵元间隔δ为4 cm的32元均匀面阵,其中M1=8,M2=4,干扰为4 kHz窄带信号,能量为10 dB,干扰方向Ωi=[90°-30°]T,阵元自噪声为-35 dB。实验结果为1 000次蒙特卡洛实验的平均结果。图2给出了此时三种不同阵元受损情景时协方差矩阵误差的变化情况。
由图2结果可知,仿真实验结果与理论分析相符,即采集信号与相邻通道重复对协方差矩阵的影响小于采集信号为0对协方差矩阵的影响,而采集信号为白噪声时对协方差矩阵的影响与白噪声能量有关。我们将进一步通过宽带仿真实验验证理论分析。上述结果同时也表明,采用估计协方差矩阵与真实协方差矩阵误差的F范数度量阵元失效对自适应波束形成的影响是合理的。

图2 三种阵元受损情况下协方差矩阵误差随白噪声能量的变化Fig.2 Variations of the estimation error of covariance matrix with white noise energy in three cases of array element damage
3.2 客观指标
常用的波束形成器客观指标包括阵增益,以及均方误差(Mean Squared Error,MSE)等,其中阵增益可用于衡量波束形成器的干扰噪声抑制性能,不失一般性,如果选择第一个传声器计算噪声功率时,阵增益定义式为
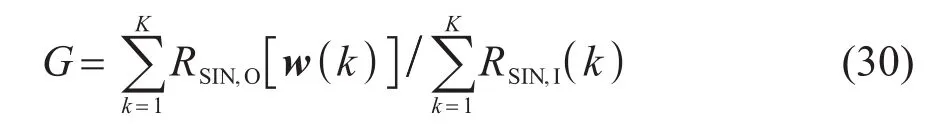
其中:RSIN,I(k)表示第k个频点对应频率的输入信干噪比;RSIN,O[w(k)]表示第k个频点对应频率的输出信干噪比。
均方误差用来评估滤波后信号和期望信号的统计误差,其定义式为
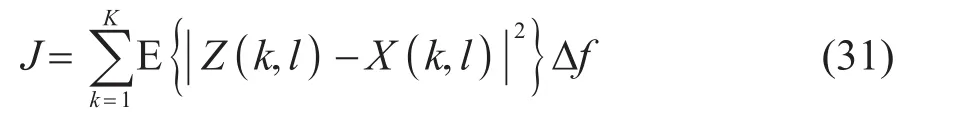
其中:Δf为相邻频点的间隔。
3.3 仿真实验
在鸣笛信号检测提取的应用场景中,往往需要较多的传声器阵元进行处理,因此本文以鸣笛应用为背景,对阵元失效的影响进行仿真和实验研究。选取汽车鸣笛信号作为期望信号放置在Ω0=[90°0°]T,选取白噪声作为干扰放置在Ωint=[90°50°]T。使用32元均匀面阵进行测试,其中M1=8,M2=4,传声器间隔δ为4.3 cm,采样率为16 kHz,实验时进行分帧处理,帧长及FFT点数为512,帧移为256。这里使用约10 s长的纯噪声段估计噪声协方差矩阵。如前所述常见的阵元失效场景包括两个传声器采集信号完全一致、信号幅度异常变小或为零、以及采集信号中只有自噪声。为了便于描述,在下文中将两个传声器采集信号完全一致定义为失效场景1,将信号幅度异常变小或为0定义为失效场景2,采集信号中只有自噪声定义为失效场景3。
首先设计仿真实验来探究三种阵元失效情景下,KP-MVDR波束形成器的阵增益及均方误差变化情况。本节选取DAS波束形成器,传统MVDR和KP-MV-DAS波束形成器进行对比,其中KPMVDR迭代次数选择为5次,仿真中的输入信干噪比(Signal to Interference plus Noise Ratio,SINR)设为0 dB,失效场景3中的白噪声能量为-10 dB,不存在误差时的参考阵增益及均方误差如表1所示。由表1结果可知,与固定波束形成器相比,自适应波束形成器具有较高的阵列增益和较低的均方误差,且三种自适应波束形成器性能大致相同。
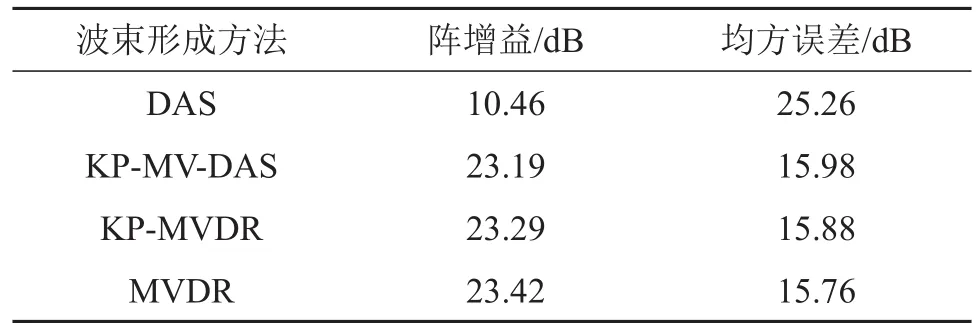
表1 不同波束形成方法在典型情况下的参考阵增益及均方误差Table 1 Reference array gains and MSEs of different beamforming methods in a typical case
3.3.1 仿真实验1
图3给出了不同阵元失效场景下,不同阵元失效数量对不同波束形成器的阵增益及均方误差的影响。由图3中的结果可知,随着阵元失效数量的增加,三种场景下所有自适应波束形成器的阵增益都有不同程度的下降,而DAS波束形成器的阵增益基本保持不变。这是由于DAS波束形成器的滤波器系数不依赖于数据,因此阵元失效不会对其产生严重影响。在所有测试场景中,失效场景2对阵增益的影响最大,阵增益产生了大幅度下降,而失效场景1和3对阵增益的影响相对较小,阵增益存在微弱下降。在所有的自适应波束形成器中,KP-MVDR波束形成器表现出较强的鲁棒性,在三种失效场景下都保持着较高的阵增益,其对应的均方误差也相对较小,优于其他两种波束形成器。
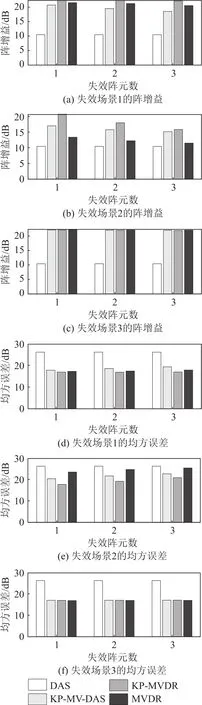
图3 受损传声器数量不同情况下不同波束形成方法的阵增益及均方误差结果Fig.3 Array gains and MSEs of different beamforming methods for different numbers of damaged microphones
3.3.2 仿真实验2
本节将研究不同阵元失效情景中输入信干噪比对四种波束形成器阵增益及均方误差的影响。仿真中固定阵元失效个数为2,其他参数同仿真实验1。图4给出了不同输入信干噪比情况下各波束形成器的阵增益以及均方误差的对比结果。由图4可知,随着输入信干噪比增加,失效场景1和失效场景3中不同算法的阵增益变化不明显。而在失效场景2中阵增益表现出不同的变化趋势,其中在绝大多数情况下,KP-MVDR以及KP-MV-DAS算法的阵增益随着输入信干噪比增加而增加,而MVDR算法的阵增益随着输入信干噪比增加反而降低。

图4 不同输入信干噪比下不同波束形成方法的阵增益及均方误差结果Fig.4 Array gains and MSEs of different beamforming methods for different input SINR
由上述两个仿真结果可知,失效场景1和3对自适应波束形成器影响较小,失效场景2即信号幅度为0对自适应波束形成器的性能影响较为严重。
3.3.3 仿真实验3
本节研究失效场景3中白噪声能量大小对自适应波束形成器的性能影响,参数设置同仿真实验1。图5给出了阵增益和均方误差随白噪声能量的变化情况。由结果可知,白噪声能量严重影响波束形成器的性能。当白噪声能量较小时,失效场景3接近失效场景2,阵增益出现明显下降,均方误差相应增大。但阵增益并非随着白噪声能量增大而不断增大,当白噪声能量过大时,阵增益会相应下降,即0 dB时的阵增益小于-10 dB时的阵增益。

图5 在失效场景3和白噪声能量不同情况下不同波束形成方法的阵增益及均方误差随白噪声能量的变化Fig.5 Array gains and MSEs of different beamforming methods for different white noise energies in the third microphone failure scene
由上述三个仿真实验可知,失效场景1和失效场景3对波束形成器性能的影响较小,失效场景2对波束形成器性能影响的较严重。失效场景3中白噪声能量的大小严重影响波束形成器的性能,但在真实场景下,阵元失效时白噪声能量通常较小,因此失效场景1对波束形成器的性能影响最小。
基于上述分析,本文针对失效场景2和3提出了一种可行的阵元受损补救方法,使用相邻通道的数据替换受损通道数据,再进行KP-MVDR和KPMV-DAS波束形成。在3.4节中,我们用实验数据进一步验证上述方法的可行性。
3.4 实际场景实验
本节以传声器阵列实录的道路实测噪声和鸣笛信号作为传声器采集信号,对比真实场景中三种阵元失效场景下各波束形成器的性能。
实验所用阵列为32元均匀矩形面阵,其中M1=8,M2=4,传声器间隔δ为4.3 cm。实验所用鸣笛信号为阵列实录鸣笛信号,阵列布放在脚手架上,阵列中心距离地面高度约为8.15 m,鸣笛声源放置在阵列正前方30 m处,高度约为0.5 m,此时期望信号方向约为Ω0=[105°,0°]T。噪声信号为同一阵列录制的真实道路噪声信号。这里使用约10 s的纯噪声段估计噪声协方差矩阵。使用实录噪声信号和实录鸣笛声信号的复合信号模拟真实行车道路时传声器阵列采集到的鸣笛信号。图6给出了实录较纯净鸣笛信号及带噪鸣笛信号的语谱图。
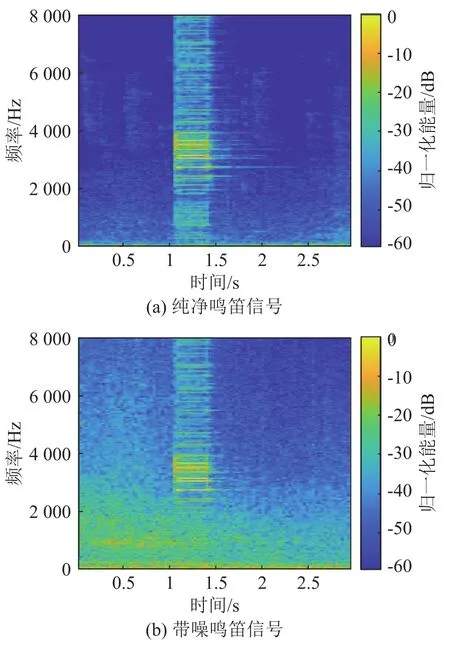
图6 纯净鸣笛信号与带噪鸣笛信号语谱图Fig.6 Spectrograms of clean and noisy horn signals.
失效场景3中的白噪声能量在实验中设置为-30 dB,其余参数设置同仿真1。四种波束形成器的阵增益和均方误差变化情况如表2所示。
由表2可得到与仿真1相似的结果,即失效场景1对自适应波束形成器的性能影响相对较小,失效场景2及白噪声能量较小时的失效场景3对自适应波束形成器的性能影响最严重。在所有自适应波束形成器中,KP-MVDR性能最优,鲁棒性也较强,在所有场景下都有最高的阵增益。表2中均方误差的性能表现出与阵增益相似的变化趋势,即失效场景1对应的均方误差最小。根据3.1节中的理论分析可知,失效场景1对应的估计协方差矩阵在F范数度量下最接近真实协方差矩阵,因此失效场景1较其余两种失效场景具有更高的阵增益及更低的均方误差。仿真和实验结果进一步验证了3.1节中的理论推导。因此,在实际应用中,当阵列检测到出现失效场景2和3时,对失效阵元使用其相邻通道的数据代替,将失效场景2和3转换为失效场景1,可以起到提升自适应波束形成器性能的效果。
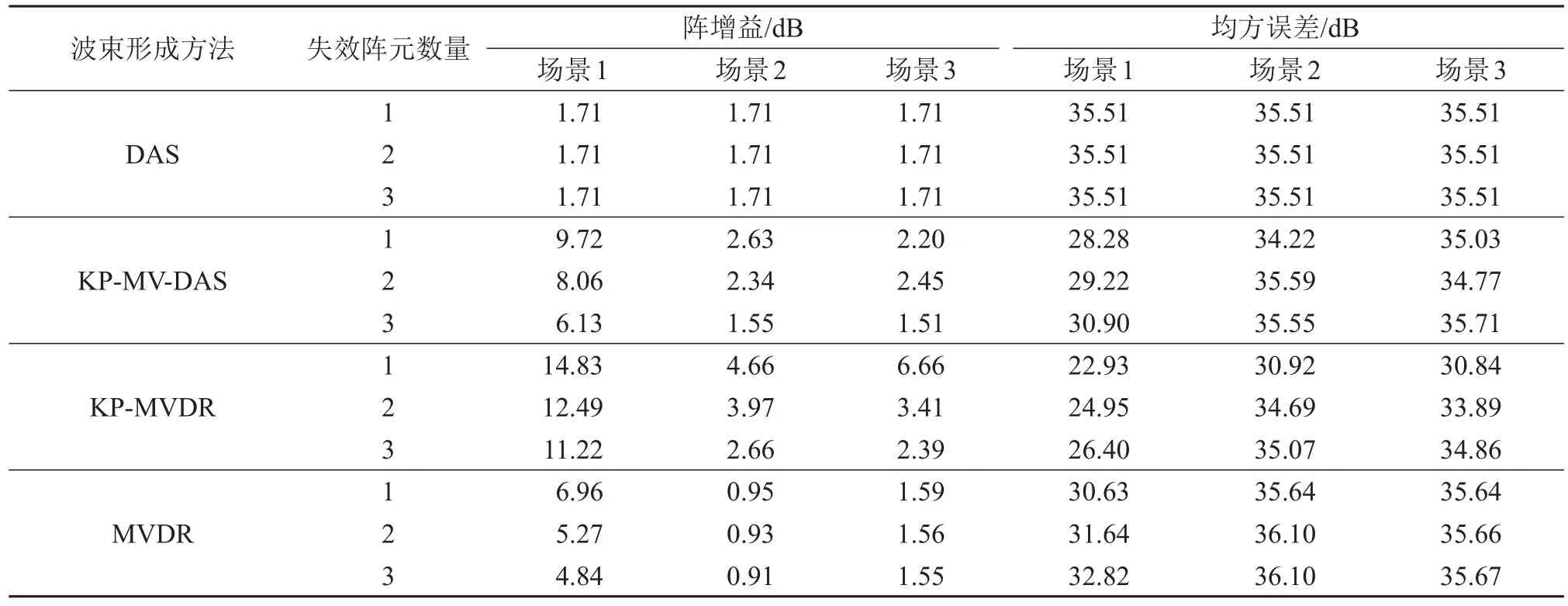
表2 三个实验场景下不同波束形成方法的阵增益与均方误差的变化Table 2 Changes of array gain and MSE of different beamforming methods in three experimental scenarios
4 结论
当传声器阵列阵元较多时,往往会出现阵元失效的情景,此时自适应波束形成器的干扰噪声抑制性能可能会有所降低。本文讨论并分析了三种常见阵元失效对最小方差无失真响应波束形成器及基于克罗内克积的自适应波束器的性能影响。仿真与实验结果表明,信号完全缺失的通道对自适应波束形成器的影响最大,信号重复的通道对自适应波束形成器的影响最小。基于此结果,本文提出了一种方便可行的信号恢复方法,即使用相邻通道代替信号缺失通道,进而提升阵元失效场景下自适应波束形成器的性能。不同于已有的协方差矩阵重构方法,本文提出的方法可以在不引入额外计算量的前提下,大幅度提高阵元失效场景下自适应波束形成器的性能。这对于真实应用场景下的中、大型传声器阵列的阵元失效问题具有重要意义。
