连栋温室内湿帘-风机流场特性
2022-10-17高振军李文杨丁小明李苇NYAMOSORBatkhuu
高振军,李文杨,丁小明,李苇,NYAMOSOR Batkhuu
(1. 三峡大学机械与动力学院,湖北 宜昌 443002; 2. 农业农村部农业设施结构工程重点实验室,北京 100125; 3. 广东省现代农业装备研究所,广东 广州510630; 4. Department of Forest Environmental Science, National University of Mongolia, Ulaanbaatar 14201, Mongolia)
与传统温室相比,大型连栋玻璃温室具有更大的利用空间,可进行更加高效、节能、科学的操作,在农业现代化进程中,得到了越来越广泛的应用,具有巨大的发展潜力.但是,由于大型连栋温室的大空间跨度造成的温度分布不均、降温困难等问题也十分明显,夏季通风不良甚至会使得温室内温度过高而休棚,无法实现周年生产[1-2].
目前,国内外对于小型温室内的温度分布和各种条件下的通风情况已有了较为详尽的研究[3-6],但针对大型连栋温室的通风情况的研究仍较少.沈明卫等[7]对塑料连栋温室进行了稳态计算,讨论了开窗形式对温室内流场的影响.王新忠等[8]、张芳等[9]对自然通风条件下,连栋温室内的热环境进行了稳态模拟.赵杰强等[10]研究了机械通风时连栋温室内温度场的分布.在国外,TEITEL等[11]研究了单跨温室中风速对温室内空气交换和通风效率的影响;LEE等[12]研究发现文洛型多跨温室由于更复杂的屋顶开窗形状,自然通风时容易出现温室内部气流分布的不稳定.上述对温室通风情况的研究大多局限在对单一流场或温度场的分析,且对湿帘-风机通风工况的研究很少,另外已有的连栋温室的计算模型多为稳态计算,忽略了对其中变化规律的总结和讨论.
近年来,将计算流体力学和试验监测方法相结合的研究方式在温室通风领域已十分成熟[13-16].通过对农业技术推广总站的连栋温室模型进行计算,揭示湿帘-风机通风条件下,其内部流场的瞬态变化特征,并在相同步长下,将温度和速度的计算结果对照分析,探究通风过程中温度场与速度场的联系,希望为进一步掌握连栋玻璃温室内湿帘-风机的降温规律,提高温室内适宜小气候的调控效率,降低运行能耗等提供有价值的参考.
1 连栋玻璃温室建模
1.1 建模对象
农业技术推广总站示范基地位于广州市天河区柯木塱(113.4°E,23.18°N),地处南亚热带,属于亚热带典型的季风海洋气候.图1为文洛小尖顶温室及结构尺寸示意图.连栋温室主体构架采用轻型热镀锌钢材料,四周覆盖5 mm厚单层玻璃.试验温室共3栋,单栋跨度9.6 m,长36 m,每栋开间数为3.肩高6.5 m,屋脊方向为东西走向跨28.8 m,脊高7.5 m ,湿帘距地高度1.6 m,风机距地高度2 m.
1.2 几何模型
按1∶1建立试验温室的几何模型,如图2所示.考虑实际过程中入口空气的流通形式以及与湿帘之间的换热,对温室内部的支撑结构等细节做简化处理.以笛卡尔坐标作为所建模型的全局坐标系,并规定x轴正方向为南,y轴正方向为东.图2a为湿帘侧,图2b为风机出口侧,温室顶部窗口关闭.将风机口设置为流量出口,湿帘处设置为自由入口,并按外界环境条件设置流入空气的参数,依靠风机出口的负压形成湿帘侧的进风条件.
1.3 计算模型
1.3.1 能量方程
采用的能量方程求解形式[17],式(1)中包括了压力作用和动能项,等号右边的前3项分别表示由于导热、组分扩散和黏性耗散所产生的能量传递.

∇·[keff∇T-∑hjJj+(τeff·v)]+Sh,
(1)
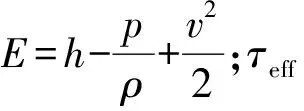
1.3.2 辐射传递方程
辐射方程可用于求解辐射传热产生的能量源项,计算过程中设置太阳辐射模型考虑自然环境中的太阳辐射.对于吸收、发射、散射性介质,在位置r处沿方向s的辐射传递方程为
(2)
式中:a,n,σs分别为吸收系数、折射系数、散射系数;σ为玻尔兹曼常数;I为辐射强度;Φ为凝聚相的散射相函数;Ω′为立体角;r为位置向量;s为方向向量;s′为散射方向散度.
1.3.3 湍流方程
模拟中湍流模型采用标准k-ε模型,考虑浮力的影响,温室内流场通过质量、动量和能量守恒方程表征,选择雷诺时均N-S方程进行求解.湍流模型方程为
E′=Gk+Gb-ρε-YM+Sk,
(3)
(4)
(5)
式中:Gk为层流速度梯度产生的湍动能项;Gb为浮力产生的湍动能项;YM为湍流膨胀过程中的耗散率;σk,σε分别为k方程和ε方程中的湍流prandtl数;Sk,Sε分别为湍流动能项和湍流耗散源项;C1,C2,C3为常数;Prt为湍流能量普朗特数.
式(3),(4)分别为标准模型的湍动能和湍流耗散的输运方程,式(5)为方程中考虑的浮力项.由于连栋温室占地面积较大,温度分布具有更大的不均匀性,选用标准模型,用标准壁面函数法进行处理将得到更高的计算效率和计算精度[18].
将温室内气体流动视为低速、不可压缩的湍流流动,建立的雷诺时均N-S方程为
(6)
(7)
式中:Ui,Uj为时均的速度;p为压力值;u′i,u′j为速度脉动值;Sji为变形率张量.
2 网格划分与数值计算
2.1 网格划分
计算模型中选取整栋温室作为计算域,对其进行以四面体为主导的网格划分,平均网格单元尺寸设置为0.25~0.50 m,考虑风机与湿帘入口处气流变化的复杂性,对模型进出口附近及壁面边界的网格进行加密处理,以保证这些区域在温度、速度梯度变化剧烈时仍有较好的计算精度.为得到网格线性无关解,反复尝试不同密度网格后,根据特征点的平均温度误差结果,最终确定计算模型的网格单元为887 590.表1为网格独立性验证结果,表中N为网格数,e为平均误差.

表1 网格独立性验证结果
2.2 数值计算
选择Fluent 软件,以上述实测结果作为初始条件进行瞬态计算.由于计算中考虑了传热模型、湍流模型、辐射模型和组分输运模型,因此采用SIMPLEC半隐式耦合算法,以提高瞬态计算的收敛性和稳定性.时间步长设置为0.08 s,每计算6步保存1次,计算600 s.关注湿帘-风机通风方式下,连栋温室内温度场和速度场的瞬态变化特征.
3 试验设计及模型验证
3.1 试验温室监测点布置
试验区连栋玻璃温室内的监测点布置如图4所示.分别在距地面0.6,2.5,4.5 m这3个水平高度的监测平面上按照图4b的布局每层选取9个监测点.对应监测点的传感器编号:距地面 0.6,2.5,4.5 m每层传感器的编号首位分别为A,B,C,图4b所标数字作为0.6 m处传感器的位置编号.在温室外1.5 m高度处设置气象监测点,监测点距边墙5 m,周围无障碍物,进行同一时刻的数据记录.试验过程中由环境监测数据采集器(SS-EST-2000)对温室内温度和风速信息进行采集.
3.2 模型验证
由于监测时间跨度较大,难以通过数值计算得到长时间连续的瞬态结果,故将6:00的试验结果作为初始条件开始进行稳态计算,将8:00以后各时刻点的稳态计算结果与试验结果对比进行误差分析.考虑到温室中监测点截面的对称性,选取A1,B1,C1这3个监测点进行验证,得到的对比结果如图5所示,图中tk为时刻,Te为温度误差值.
0.6~4.5 m高度显示的最大温度误差依次为1.80,3.20,3.90 ℃,平均温度误差依次为1.17,1.90,2.34 ℃.从误差分析结果来看,随着高度增加,计算值与实测值的误差有增大趋势,分析认为主要由于模拟过程中,连栋温室顶部内遮阳对太阳辐射的吸收作用难以准确模拟,使得温室顶部的试验值普遍大于计算值.总体上,产生的误差较小,计算结果与试验结果变化趋势一致,表明建立的计算模型是可靠的.
4 计算结果分析
4.1 湿帘-风机通风过程分析
4.1.1 温度场分析
图6为温室中部截面的整体温度T的变化,在湿帘-风机系统通风的初始时刻,湿帘入口及入口以下区域降温效果明显,但之后的气温变化与小型温室的变化趋势差别较大.小型温室内地面附近先降温,距地面较高区域后降温,通风过程中的温度差异主要表现在垂直方向的分布不均,且窗口处常常存在受速度场影响的明显的带状低温区域[16].而在连栋温室的实际计算中,温室内的气温随时间变化表现为梯度推进的降温特征,湿帘侧到风机侧产生明显的温度梯层,温度场的分布受空间跨度影响较大.
将图6所示的计算的温度瞬态变化数据量化分析,取不同时刻2.5 m高度,分别距湿帘侧6,15,24,33 m的温度值,得到图7所示的曲线图.由图可知,在湿帘侧开始进入较冷空气后,连栋温室内的大环境温度已经开始逐渐下降,越靠近湿帘侧降温越明显.最终表现出明显的梯度降温和小幅度整体降温共存的温度变化特征.当温度下降到34.00 ℃时,靠近风机侧所用时间约为湿帘侧的4倍.从湿帘侧开始,4个监测点温度开始快速下降的时间分别为0.8,2.0,4.0,6.0 s.越靠近湿帘侧,最终稳定的温度值也越小,湿帘附近到风机区域气温稳定值依次为31.15,31.86,32.42,32.67 ℃.
4.1.2 速度场分析
图8为连栋温室中部纵截面的速度场,图中v为速度.从图中可以看出,在重力、浮升力等因素的共同作用下,连栋温室内的速度场存在湍流现象.风机出口速度变化剧烈,随着通风过程的不断进行,逐渐形成了从湿帘入口向下贯通风机口的高速气流带.通风初期(t为0~12.8 s)风机对温室内整体气流场的带动作用明显,温室的绝大部分区域受风机影响均产生了一定的流动速度.随着通风过程的进行,湿帘侧进入的气流速度较其他区域高并逐渐发展,最终成为主导连栋温室的速度场.而温室内最初产生的低速流场,在湿帘侧的高速气流场发展过程中受其高速核心(最高速度可达1.6 m/s)的影响先增强,之后逐渐变弱,当湿帘侧到风机侧的气流场完全稳定后基本消失.
4.2 不同风机流量的瞬态温度分析
为分析不同风机流量下,湿帘-风机系统的降温效果,提取了风机流量44 500 m3/h和89 000 m3/h,2.5 m 高度下,距湿帘入口6,15,24,33 m的4个位置在风机开启后0~50.0 s的瞬态温度变化情况如图9所示.
由图9可知,随着与湿帘入口距离的增加,降温所达到的最终温度逐渐升高.当风机流量增加1倍后,温室内温度趋于稳定的时间缩短了一半左右,最终降温效果表现的差异随着距离的增加越来越明显.在距离湿帘入口6,15 m处,不同风机流量下产生的最终降温温差为0.14 ℃,而距湿帘24,33 m处,温差达到了0.46 ℃和0.81 ℃.因此,风机流量主要影响降温时间,对温室内产生的最终降温效果差异较小.在温室内降温速度需求并不迫切时,可适当降低风机流量以减少能耗.
5 结 论
建立了华南地区连栋玻璃温室湿帘-风机通风的稳态和瞬态计算模型,并通过试验,验证了计算模型的准确性,进而得到了连栋温室内温度场和速度场的变化情况,分析得出如下结论:
1) 大型连栋温室采用湿帘-风机通风时,其降温过程的瞬态温度场呈梯层分布,从湿帘侧向风机侧分层推进,同时温室内整体环境温度以微小幅度持续降温,最终达到稳定状态.
2) 温室内风机口速度变化剧烈,初始时刻的速度场以占据整个温室的低速流场为主,之后受穿堂现象影响,由湿帘侧贯通风机口的高速气流场发展为温室内主要的流场特征,初始的低速流场逐渐消失,最终地面附近的空气更新率将保持在约0.8 m/s的稳定状态.
3) 在大型连栋温室运行中,湿帘-风机通风过程中,速度场中全局性的低速流场和发展形成的高速贯通流场,直接影响了温度场整体小幅度降温和由湿帘侧梯度降温的瞬态变化特征.因此,针对连栋温室通风过程中的速度场进行优化是提高其降温效果的关键;风机流量的提高主要表现在温室内降温速度的缩短,对最终达到的降温效果影响较小.越靠近湿帘侧,不同风机流量造成的这种降温效果的差异越小.
4) 在大型连栋温室设计中,可适当抬高湿帘高度,预计稳定后的气流场可对更大区域产生同样的降温效果;若需增大温室占地面积,在保证湿帘-风机系统仍可形成稳定的贯通气流场的基础上,适当增加湿帘与风机的距离,同样可保持现有的通风效果.后续可根据不同温室长宽比对湿帘-风机运行的流场特性进一步研究,以得到对温室设计的更多指导.
