基于混合蚁群算法的重调度低碳城市配送

张明伟，李 波，屈晓龙

(1.天津仁爱学院 经济与管理学院，天津 301636；2.天津大学 管理与经济学部，天津 300072)

0 引 言

车辆的碳排放量与行驶速度密切相关，受早晚交通高峰的影响，城市内车辆平均行驶速度在不同时段变化明显，形成时变网络，从而影响车辆的碳排放量[1]。城市车辆配送路径问题(vehicle routing problem，VRP)已经越来越多考虑了时变网络影响[2,3]。但是还需考虑新到达订单对调度方案造成的扰动[4]。目前已有学者对客户订单的调度周期等实际配送问题进行研究[5]，并对随机到达的订单扰动进行重调度来获取更优方案[6]。车辆选择不同路径，平均行驶速度及行驶距离会有差异，碳排放量也会受到显著影响[7,8]。蚁群算法在路径优化过程中存在效率较低、易早熟等缺点，可通过改进算法流程和改进信息素更新方式，来提高算法效率，避免陷入局部最优[9]。

本文将以碳排放量最小作为主要优化目标，根据随机订单到达的时间安排调度，研究时变网络、柔性路径下配送货车动态重调度的问题。即RTVVRP-PF(rescheduling of time-varying vehicle routing problem with path flexible)。采用模拟退火与蚁群混合的算法求解模型，以避免陷入局部最优，提高算法收敛速度；引入碳排放因子，改进信息素浓度更新方式；使用自适应精英个体繁殖策略提高算法效率。

1 问题描述与假设条件

1.1 问题描述

本文以城市内货物配送为研究对象，货运车辆从一个配送中心出发，为多个不同时间窗口的客户需求进行配送。车辆可以在多条柔性路径中，选择到达客户节点的最佳路径，并且在时变网络下，车辆速度随道路拥堵程度、交通高峰期动态变化，车辆速度的变化能够直接影响车辆的碳排放量大小。

(1)动态重调度对解空间的影响

调度池中新订单的增加，将减少优化方案中的变量约束，扩大全局优化的解空间，从而找到更优的可行解，如图1所示。

图1中，原调度方案，车辆配送订单2时，部分行驶时间处于交通拥堵期，车辆的速度降到25 km/h，由于速度较慢，车辆在交通拥堵期将产生大量碳排放。

假如在原调度方案中的车辆还没有出发时，加入新订单，一起优化调度，新订单路径平均速度较快(35 km/h)，部分服务时间在交通拥堵期内不产生碳排放量，并且订单2由于重调度，避开了高峰，速度变为55 km/h，将减少大量碳排放。因此，以一定周期加入新订单进行多次动态重调度，比一次性的静态调度具有更大的解空间。

(2)时变网络下柔性路径对碳排放量的影响

在现实的城市配送道路网络中，网络节点之间往往有多条路径连通，即存在柔性路径。在早晚交通高峰期影响下，不同路径(路段)上，车辆平均速度变化较大。车辆在时变网络的不同时段，通过选择碳排放量较小的路段组成的路径，可以减少碳排放量。

RTVVRP-PF模型以动态重调度的方式为基础，考虑了在车辆平均行驶速度受交通影响的时变网络下，将一次性的静态车辆调度分成多个阶段，即随着客户订单的不断到达，在积累一定时间或一定数量的订单后，及时安排重新调度，通过新旧订单的混合来重构解空间，以使得车辆配送尽量避开交通拥堵期，提高车辆平均行驶速度来减少碳排放量。并且为了贴合实际工况，在模型中考虑柔性路径、动态载重、时间窗口约束等因素，并在模型中这些因素整体优化，以达到在VRP中减少碳排放的目的。

1.2 符号说明

模型中的变量定义如下：

V：节点集合，且V=1表示配送原点，V=(2, 3, …，N) 表示客户节点集合；

E：网络图中的弧集，i，j为任意两个客户节点，E={(i,j)|(i,j∈V且i≠j)}；

r：路径上的路段，r∈{1, 2, …，R}；

k：重调度次数，k∈{1, 2, …，K}；

m：配送车辆， ∀m∈M；

g，G：车辆的实时载货量和最大载重；

qj：节点j的货物需求量；

tj：车辆到达客户节点j的时刻；

tsj：节点j的服务时间；

tsm：车辆m的装载时间；

1.3 条件假设

(1)配送原点拥有足够多的载重量相同的车辆。

(2)每次调度中，每个客户只接受一辆车辆配送服务。

(3)车辆到达客户的时间具有时间窗口限制。

2 模型构建

2.1 碳排放量计算

车辆碳排放主要由车辆行驶过程中所消耗的燃油产生，车辆燃油消耗估算的方法分为实验法(MEET)与模型法(CMEM)两类。模型法多采用燃油消耗量为目标建立模型，来估算碳排放量。但是模型法受到燃油不能完全燃烧的影响，车辆在不同速度下，燃油消耗量与碳排放量之间关系并不是恒定的，会发生变化，因此会影响时变网络下计算碳排放量的准确度[10]。MEET法应用范围较广[11]，本文采用MEET方法，即通过对货运车辆的尾气排放污染进行大量实验分析，直接给出不同类型空载的货车在不同速度v(km/h)下的碳排放量函数θu(g/km)和系数a，并可根据配送车辆类型和性能，对系数进行调整[12]，计算公式表示为

(1)

为适合在城市内范围进行配送，本文选用载重量为4.5吨的货车，根据文献[12]，a0,a1,…，a6的取值依次为110,0,0,0.000 375,8702,0,0。

货运车辆的碳排放量与载货量成正比关系，文献[12]中不同类型车辆在不同速度下，车辆满载的碳排放量θl(v)的计算公式为

(2)

根据货运车辆的载重量，b0,b1,…，b5取值不同，装载量4.5吨车辆的取值依次为1.27,-0.002 35,0,0,-1.33。装载量4.5吨车辆满载与空载相比较，不同速度下，碳排放量系数的变化如图2所示。

可以看出，4.5吨货车满载下，速度v高于23 km/h后，速度越快，碳排放系数越低，单位碳排放量越少。

综上，某货运车辆m在速度v下，实时载货量gm，其动态实时碳排放量θ可以表示为

(3)

2.2 服务时间

服务时间包含货运车辆装车、卸车和与客户进行手续交接的时间，在服务时间内车辆不产生碳排放量。车辆装载在配送原点完成装载，因此其装载时间tsm不计入车辆行驶调度模型。客户j的服务时间tsj只需要考虑卸载时间tsj1和手续交接时间tsj2，卸载时间与客户j的需求量qj和单位时间卸载量qt(吨/小时)相关，即：tsj1=qj/qt。 如果tsj1=0， 即没有货物卸载，则tsj=tsj2=0， 表示在没有到达客户节点时，服务时间为0。客户j的服务时间可以表示为

(4)

2.3 模型建立

RTVVRP-PF重调度时变网络下柔性路径低碳城市配送模型中，选取3个优化目标：所有车辆一天配送过程产生的碳排放量总和C最小，车辆行驶的总里程D最小，车辆总行驶时间T最小。C为主要优化目标，车辆碳排放量和D密切相关，且D也为VRP主要优化目标，另外，由于存在配送时间窗口约束，且T与车辆司机、车辆日常管理成本密切相关，因此也非常重要。本文选取C、D、T作为模型的3个优化目标。

T、D、C优化目标函数分别为

(5)

(6)

(7)

目标函数约束条件S.T.

(8)

(9)

(10)

(11)

(12)

(13)

(14)

式(8)表示车辆最大负载限制；式(9)表示客户时间窗口约束；式(10)表示车辆完成任一客户e的配送任务后需要离开；式(11)表示车辆从配送原点出发一次，完成全部配送任务后需要返回原点；式(12)表示路径路段的决策变量；式(13)表示选择客户节点的决策变量；式(14)表示重调度决策变量。

3 算法设计

VRP属于旅行商问题，早被验证为NP完全(non-deterministic polynomial complete)问题，难以使用数学解析的方法进行求解[13]。智能优化算法已经公认对此类NP完全问题有较好的优化效果。蚁群算法(ant colony optimization，ACO)和模拟退火算法(simulated annealing，SA)在VRP优化求解中效果较好[14,15]。ACO是一种群智能优化算法，具有记忆性，利用蚂蚁的信息素浓度变化来选择和构造可行解。ACO每次都需要对整个种群重新构造，因此效率较低，而且容易陷入停滞。SA以某种概率接受更新解，容易跳出局部最优和停滞，且控制简单，编码易实现，但是计算时间较长，寻优效果一般，优化效率不高。

本文将上述两种算法的优点结合，提出混合蚁群算法SA-ACO，算法通过对SA中退火温度的控制，实现快速收敛，并利用SA的Metropolis准则防止陷入局部最优和过早停滞现象。通过ACO中的多参数信息素浓度计算来更新种群，增加种群的记忆性，并设计了碳排放因子，以增强种群优化的方向性。SA-ACO的算法流程如图3所示。

跳出内循环的判断标准为达到设定的某一个循环次数的常数值Cr1，跳出外循环标准为设定的某一个循环次数常数值Cr2内最优解的适应度不再发生变化。

SA-ACO算法中按照Metropolis抽样准则来接受个体si(t)是否更新为s′i(t)， 避免早熟或停滞。接受概率函数Ω为

(15)

其中，Г为退火为温度控制参数，其迭代计算见式(16)，L为算法的迭代次数

(16)

3.1 算法编码

SA-ACO算法采用实数方式编码，每个可行解为一个两行的矩阵，矩阵的第一行为配送客户节点顺序的信息，数字“1”表示配送原点，车辆从原点出发，完成配送任务后返回原点。可行解矩阵第二行为柔性路径选择信息，并且部分节点之间的路径包含多个顺序排列的路段，如图4所示。

图4第一行编码中 [1,4,3,11,1] 表示一个配送车辆从原点“1”出发，顺序到达客户节点4、3、11进行配送服务，最后返回原点。第二行路径选择信息，即车辆在1、4节点之间选择了第2条路径，4、3节点之间选择了第1条路径，3、11之间选择了第3条路径，从客户节点11返回原点选择了第2条路径。其它配送车辆行走信息依次类推，直到所有客户配送服务均完成。

3.2 适应度计算

SA-ACO算法中，种群个体的适应度与优化目标相关，模型包含碳排放量C、总行驶路径D和总行驶时间T这3个优化目标，存在Pareto解集。3个优化目标单位不同，且数量级相差较大，在个体适应度计算过程中需对优化目标的数量级进行调整，以便适合其权重系数。本文采用自适应的适应度函数f(s)来消除多个目标数量级的差别，f(s)表示为

(17)

其中，Cmax(S)、Dmax(S)、Tmax(S) 表示某一次迭代种群中，个体s的碳排放量、总行驶路程和总行驶时间的最大值，λ1、λ2和λ3分别表示三者权重系数，需要根据企业对三者的关注程度决定权重系数。

3.3 个体更新

本文提出自适应精英个体繁殖策略来更新个体，来保证能够搜索到全部解空间，动态保留精英个体的优良基因，以提高算法进化效率。

SA-ACO的种群个体采用两点局部更新的方式，如图5所示。

在客户配送节点信息编码中，将每台车辆出发的原点设为编码1，找到所有的U个车辆配送原点“1”，随机选取第u1和u2两个配送原点，将两个配送原点中间的编码按照ACO中信息素浓度进行重新构造，两个随机点之外的其它部分的信息编码直接复制，构成新的种群个体。其中这两个点之间的长度u12的计算公式为

(18)

式(18)中int[ ]向表示下取整，fmax(S) 为这一代群体中的最大适应度值，并且如果u12>U-u1， 则u2为个体的最后一个配送原点，即u1之后的部分全部更新。

自适应精英个体繁殖策略，能够快速搜索到全部解空间，按照信息素浓度构造个体局部，能够使其更新具有方向性的同时，保留其它部分的优良信息。

为增加模型中的碳排放量优化目标效果，并兼顾总行驶里程和总行驶时间的优化目标，本文在构造ACO的信息素能见度和信息素增量更新时，设计了包含碳排放量因子的多因子计算方式。

(19)

其中，allowedj′表示还没有配送的客户节点集合。

(1)包含碳排放因子的多因子能见度更新

(20)

(2)包含碳排放的多因子信息素增量计算

(21)

其中，0<σ≤1，为信息素蒸发速率。

(22)

其中，ε1、ε2、ε3为权重系数。

4 仿真算例

4.1 算例数据

为验证RTVVRP-PF模型与算法的有效性，尽量贴近现实城市配送状况且不失一般性，本文依据我国城市的配送数据的统计分布，利用计算机生成符合统计分布的随机算例数据。

城市内配送，客户的需求量一般较小，许多城市限制配送货车的载重量，一般不使用较大型货车。由于5吨以下的异质货车(车型不同、载重量不同的货车)，碳排放量差异不大。所以这里使用最大载重量G=4.5吨的同质货车(车型一致的货车)进行配送运输的模拟计算。

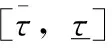
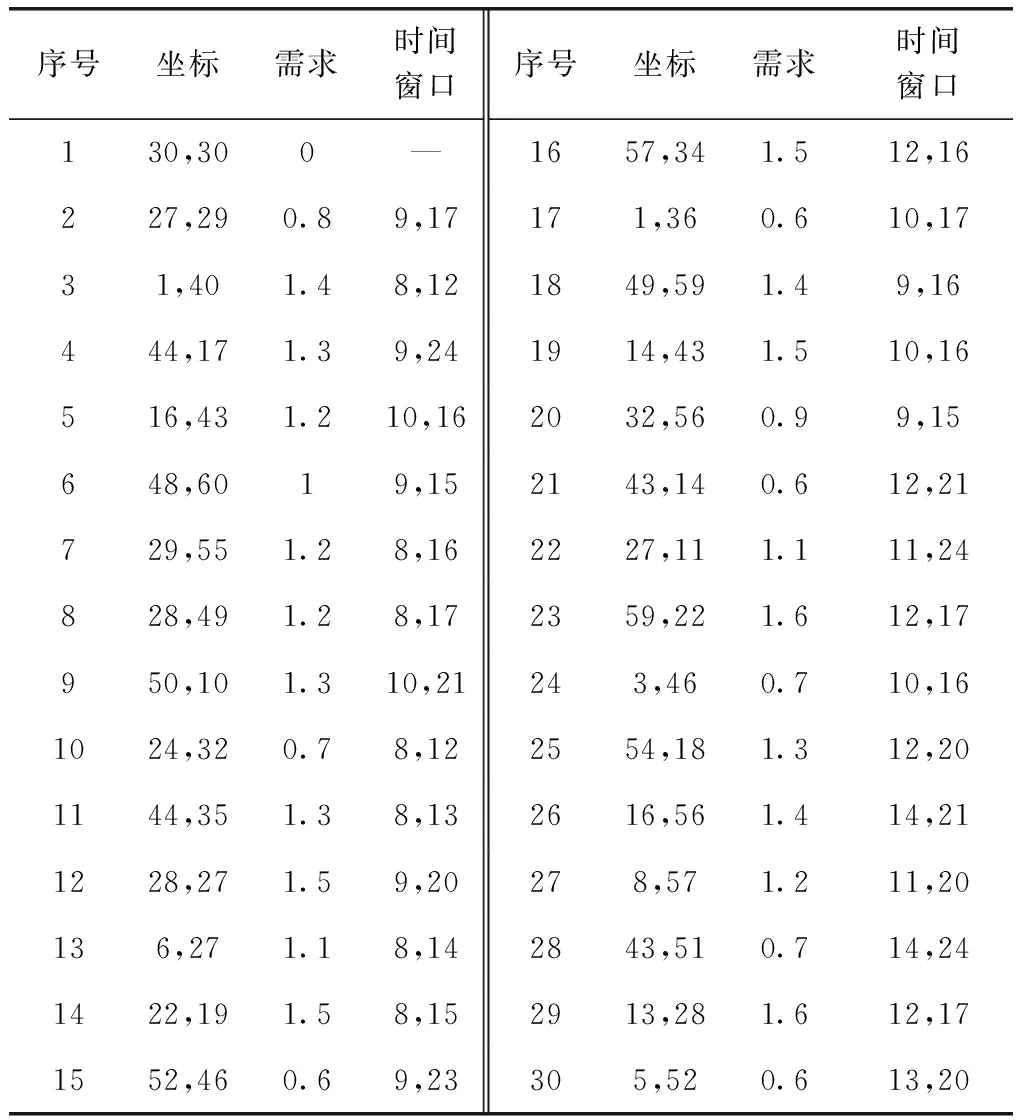
表1 随机节点的坐标、需求量(吨)和时间窗口

由于相同时刻，城市内各条道路的车流密度不同，车辆的平均行驶速度也不尽相同，有些城市的快速路和拥堵路段与其它道路的平均速度差异较大。随机选取10%的路径，按照较慢速度[20～40] km/h和较快速度[55～70] km/h，产生以5为步长的整数平均分布作为车辆行驶速度。两节点间不同路段，速度差异较大的路径，则按照均匀分布随机产生速度和路段长度百分比，见表2。

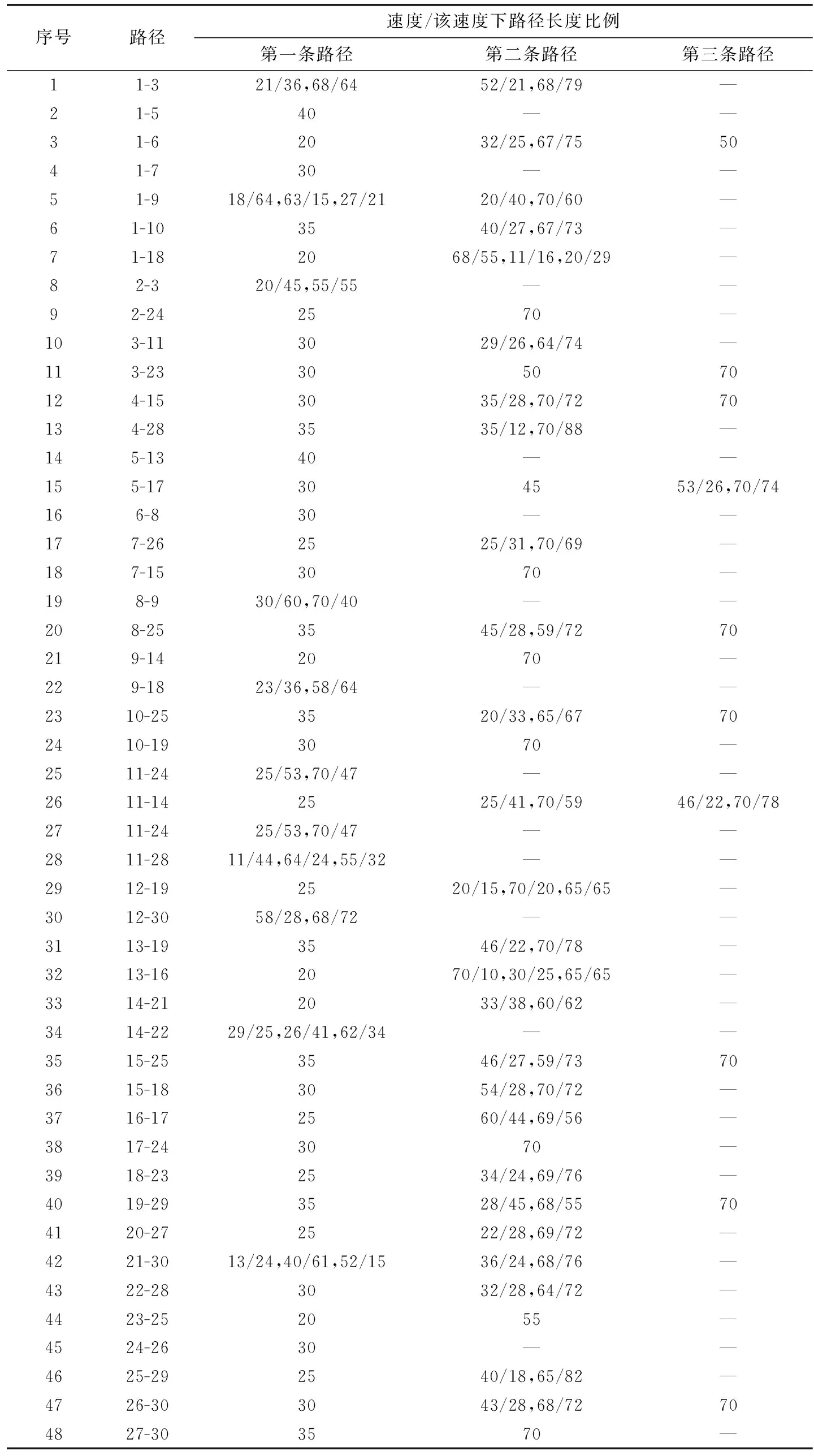
表2 柔性路径的速度/(km/h)和路段长度/%

利用交通出行网以及地图软件，统计整理一般城市各个时段道路的平均行驶速度，见表3。表2中的路径为柔性路径，所有柔性路径的平均速度为60 km/h。按照表2中柔性路径不同时段的平均速度与柔性路径平均速度60 km/h的比值，来确定柔性路径在不同时段的速度系数(见表3)。则柔性路径在不同时段的速度为表2中的速度乘以不同时段下的柔性路径速度系数。

柔性路径下，两节点之间多条路径的长度不同，这里将第二、三条路径按照第一条路径的长度以分布函数按照一定比例进行放大，放大的比例服从U(1，1.3)平均分布，见表4。

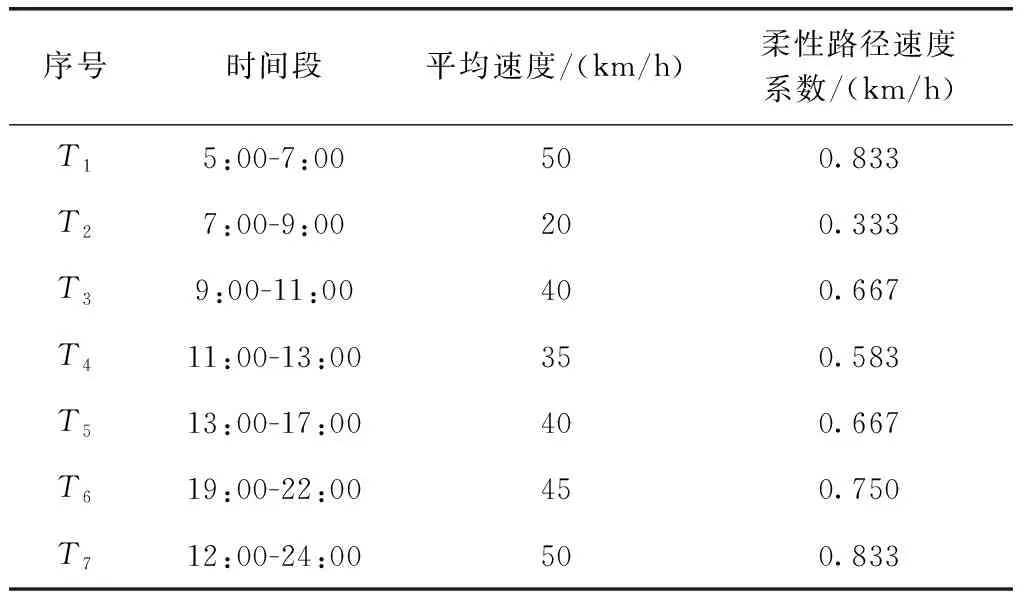
表3 车辆不同时间段的平均行驶速度

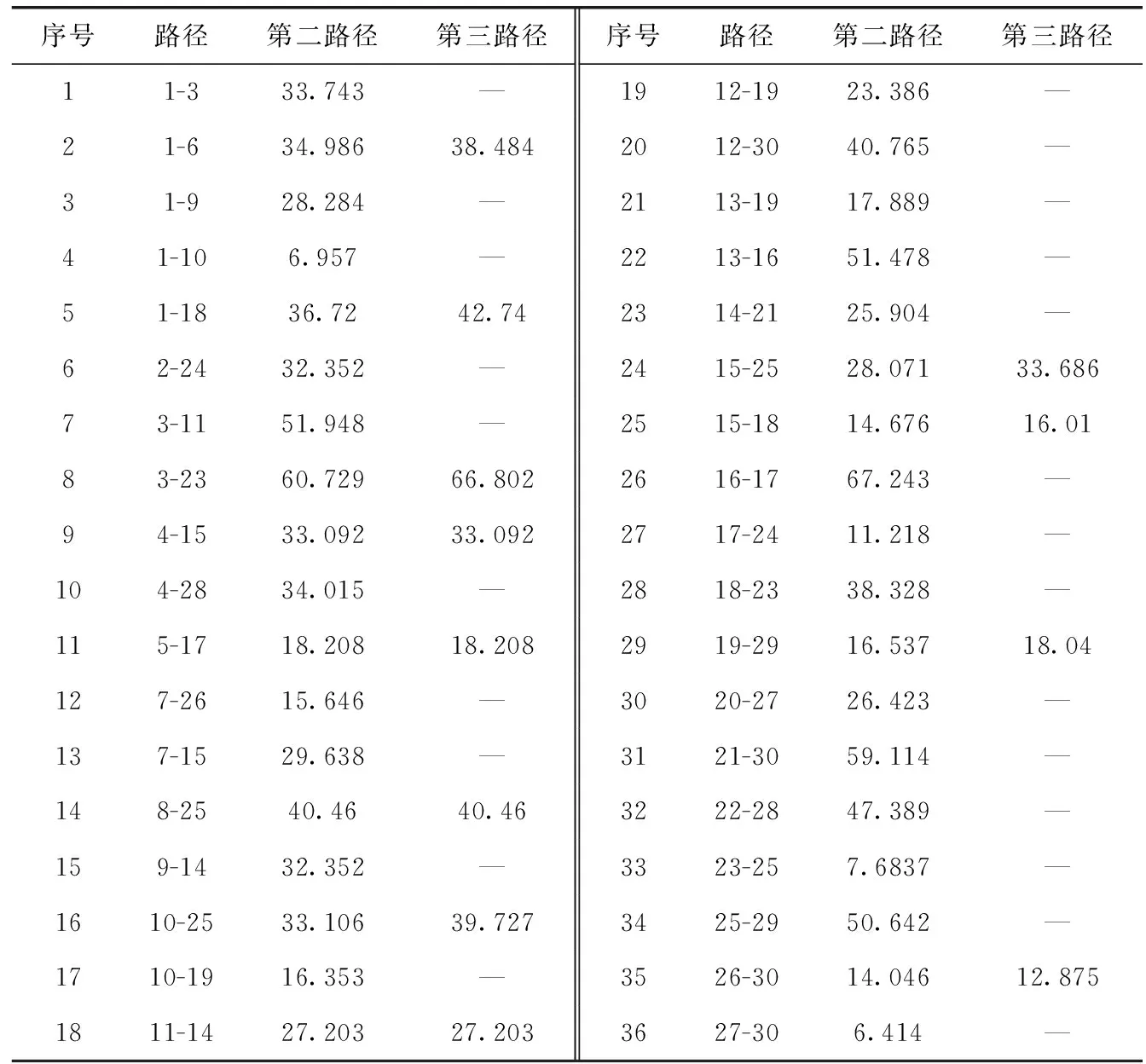
表4 柔性路径的第二、三条路径长度/km

4.2 仿真结果

本文按照4.1节中的数据进行仿真运算。使用Matlab2019a版本进行建模优化，种群规模取500。参数设置直接影响算法求解的效率与效果，本文采用均匀设计试验法来确定参数。算法参数中退火初始温度Г0=1500，降温系数0.99，内循环次数Cr1=1000，算法终止(跳出外循环)条件为Cr2=1000次迭代内，算法最优解适应度不再变化。算法的路径选取概率函数中α和β的数值取值为1，信息素的蒸发率σ=0.58。优化目标权重的系数λ1、λ2和λ3取值均为1，即企业对3种优化目标的重视程度相等。

重调度过程中，需要统计订单的到达时间，假设7点半之前，前一日未配送订单和新增的订单为客户节点2～15的订单，并且7点半之后，每1.5小时，新增5个客户订单，单位货物的卸载时间qt=0.35吨/小时，每个客户节点的手续交接时间tsj2=0.2小时，重调度后，拣货和装车的时间tsm=1，订单到达时间见表5。

表5 订单到达时间

分别采用动态重调度和静态调度方式进行仿真对比运算。首先采用动态重调度方式，即按照表5的订单截至时间进行4次调度，并且每次重调度，都将上一次没有出发的货车和订单重新加入新的调度方案，调度完成后，经过1小时拣货和装车，货车可出发。如果重调度时货车已开始装车，则该货车和订单不能加入新的调度方案。然后采用静态调度方式，即只进行两次调度，在7点半进行2～15客户节点订单调度，在12点进行16～30客户节点订单调度，并且第2次调度时，不加入第1次调度中没有出发的货车和订单。分别采用两种调度方式，各进行30次优化运算，取平均值，结果见表6。

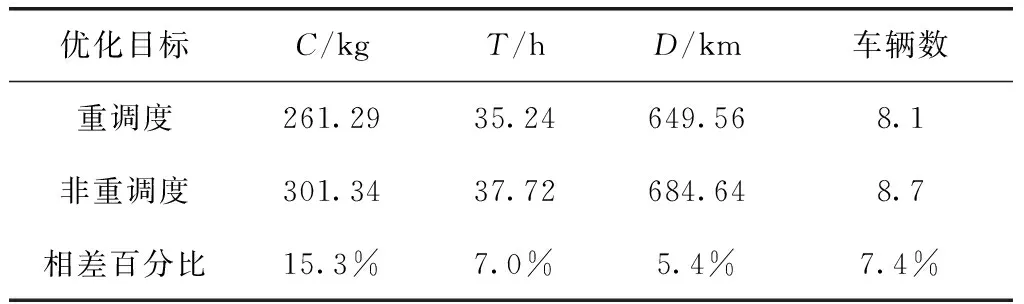
表6 动态重调度与静态调度结果对比

由表6可以看出，与静态调度方式相比较，采用动态重调度方式，在碳排放、总行驶时间、总行驶里程和使用车辆数方面均有所降低，尤其碳排放量C(kg)降低了15.3%，这主要是因为重调度使得优化空间加大，更多的车辆可以避开交通拥堵期，从而使得碳排放量等指标能够明显减少。

以30次优化计算中的一个重调度方案为例，重调度优化方案见表7，优化后的碳排放与总行驶时间和里程见表8。

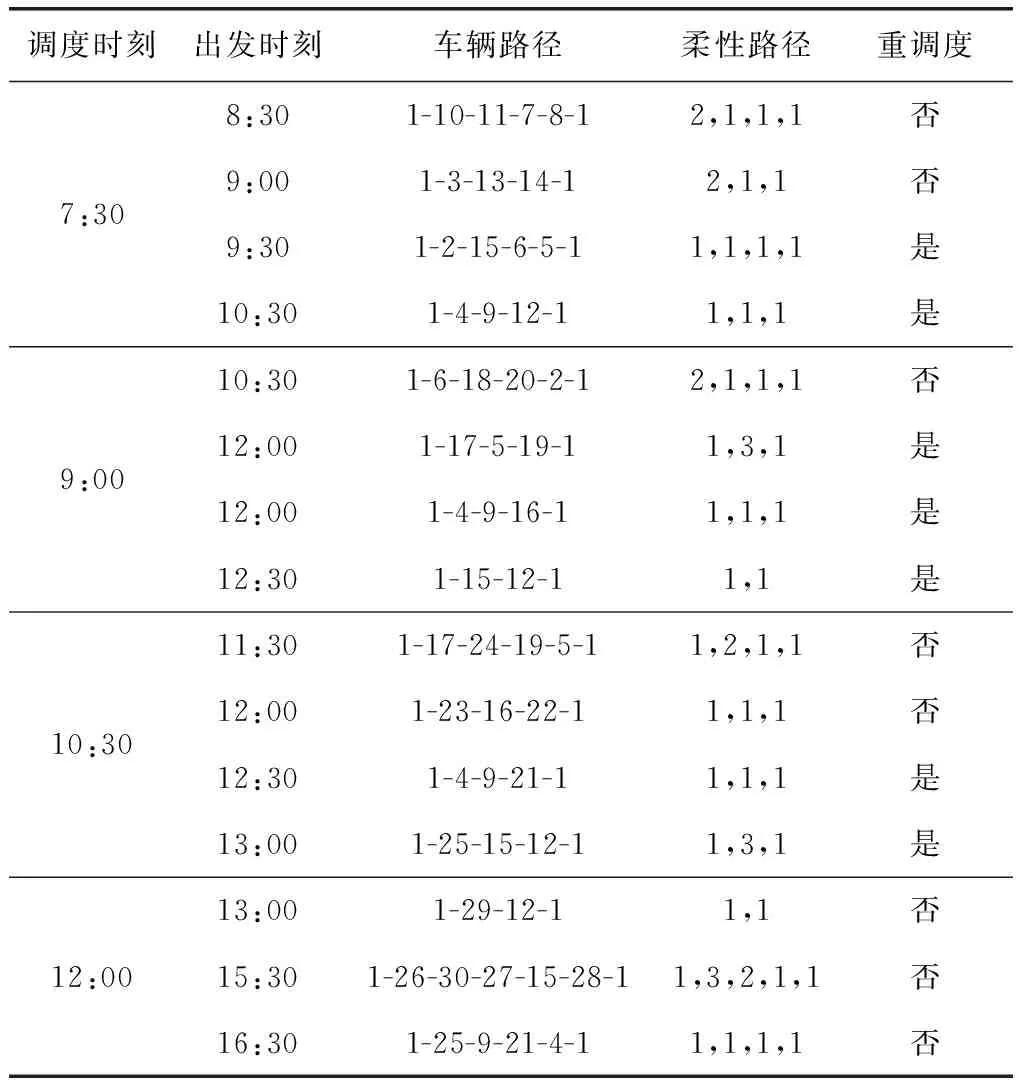
表7 重调度优化方案

由表7可以看出，在当日7点半时，对客户节点第2～15的订单进行调度，共安排4辆货车，最早货车8点半装载货物后出发。截至到当日上午9点时，接到客户节点16～20的新订单，这些订单与第一次调度时尚未开始装车的订单(分别安排在9点半、10点半装完车)，即客户节点2、4、5、6、9、12、15的订单一起进行第2次重调度，然后在上午10点半与上午12点，以相同方式分别进行了第3次和第4次重调度，共使用货车8辆。

图6为车辆配送路径，可以看出，部分路径有交叉，主要原因是订单配送是经过多次重调度产生的，以及优化目标中增加了减少碳排放目标。

多目标函数的Pareto解与各优化目标的权重系数相关，RTVVRP-PF的3个优化目标可以根据企业对优化目标的需求程度来确定。本文对3个优化目标给出参考范围。创建Pareto非支配解集合，根据支配关系进行Pareto分级，将级别最高的解放入Pareto非支配集合中，若非支配解集规模超过设定值，则进行修剪。利用上述方法求解得到10个Pareto非支配解，见表8，并分别求出了3个优化目标的极小值分别为碳排放252.45 kg，总行驶时间33.28小时和总行驶里程631.36 km。

表9为这次调度的碳排放、总行驶时间和里程。并且，为验证柔性路径和动态负载对配送优化目标的影响，在这个调度方案中，分别统计了相同调度方案下，如果使用最短单一路径和货车空载、满载的情况下，车辆的碳排放量、总行驶时间和里程变化。

由表9可以得出，如果不使用柔性路径，而使用单一路径，并且是最短路径，优化后，虽然总行驶里程稍有降低，但是碳排放量增加了11.2%，总行驶时间增加了9.2%，因为在柔性路径状况下，车辆在道路拥堵时可以选择速度更快、碳排放量更低的较长路径，说明柔性路径更加符合实际配送工况。由表9还可以得出，不考虑动态负载的影响，分别直接使用固定的货车空载和满载质量来计算碳排放量，与考虑动态负载相比，碳排放量分别相差7.5%和6.5%，表明动态负载对货车碳排放量的影响是比较显著的。

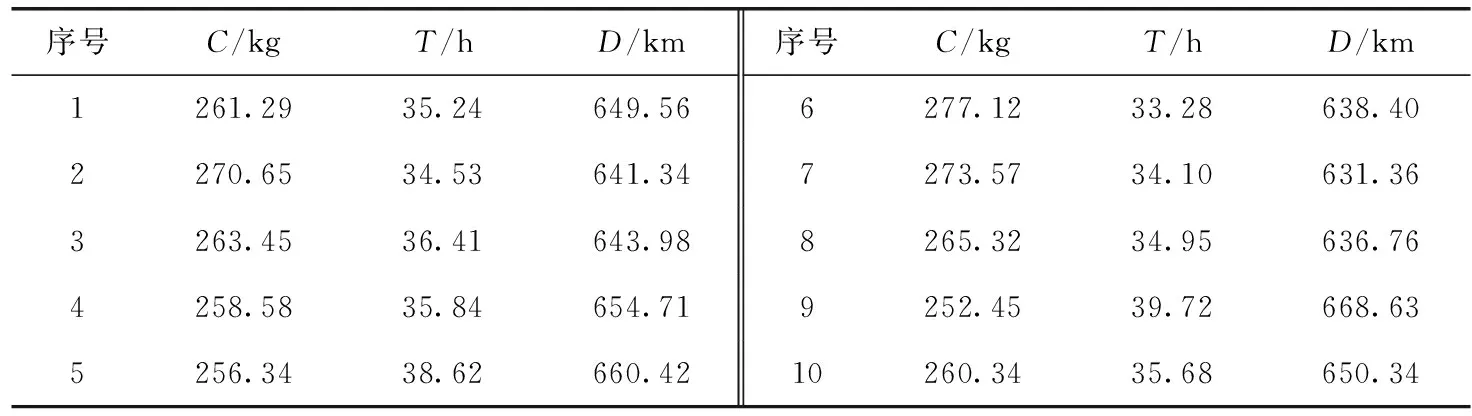
表8 Pareto非支配解集

表9 柔性路径及动态负载对优化目标的影响

为验证分路段对城市配送碳排放量的影响，计算表7优化方案中的3个包含分路段的路径碳排放量。当分路段时，分别计算每个路段的碳排放量并求和，当不分路段时，按照整条路径的平均速度计算碳排放量，计算结果见表10。可以看出，城市配送中，分路段对碳排放量影响较大，尤其是各路段速度差异较大时，而同一时间，城市道路拥堵程度往往差异较大，所以在城市配送调度优化过程中，不能忽略分路段对优化结果的影响。

表10 分路段对优化目标的影响

为验证SA-ACO算法的效果，分别使用粒子群(particle swarm optimization，PSO)、SA和ACO算法，按照4.1节随机算例数据，采用CPU3.3GHz，内存8 G，64位Windows10操作系统的计算机，SA中采用实数编码，降温系数取0.99，初始温度1500，每个温度迭代次数1000；PSO中惯性权重0.73，两个加速因子均为1.21；ACO算法的参数取值与SA-ACO相同。各计算30次，结果取平均值。均采用均匀设计方法设置算法参数，结果见表11。

由表11可知，SA-ACO在碳排放量、总行驶时间、总行驶里程和使用运输车辆数量方面实验结果的数值均为最小。在计算耗时方面，由于SA-ACO混合蚁群算法在构造路径方面计算量较大，相比较于PSO算法中寻找粒子方向的更新方式，SA-ACO计算耗时略高于PSO算法。

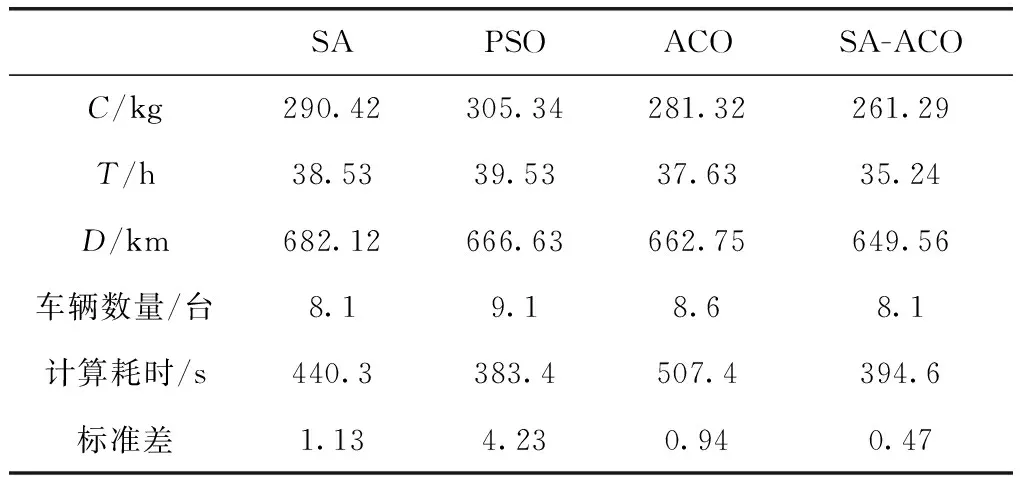
表11 算法效果比较

由图7可知，与其它算法相比较，SA-ACO的收敛速度在100次迭代后，明显优于其它算法。

为进一步分析SA-ACO算法效率，本文采用TSPLIB中的3个经典的算例进行优化分析，算法参数的取值与上述RTVVRP-PF模型相同，优化结果见表12。

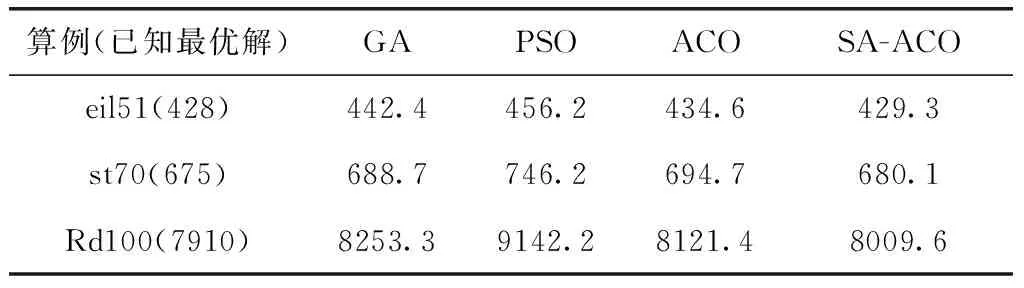
表12 TSP模型算法效果比较

由表12可以看出，SA-ACO对TSP以及VRP问题的优化计算具有较好效果。

5 结束语

在城市配送RTVVRP-PF模型中，首先验证了动态重调度和静态调度相比较，对减少碳排放量的效果明显。其次，提出SA-ACO算法，提高了算法效率和跳出局部最优能力；设计了自适应精英个体繁殖策略，提高了种群优良基因的个体数量；引入包含碳排放的多因子算子，增强信息素更新的方向性。最后，按照城市配送实际工况，随机生成算例，通过对算例的运算结果进行分析，验证了模型在动态重调度、柔性路径、动态负载和分路段方面，对减少碳排放量效果显著，同时验证了SA-ACO算法的高效性。