含齿面剥落缺陷影响的共轴对转轮系振动特性分析
2022-10-17杜正柱许立新
杜正柱, 许立新,2, 牛 坤
(1.重庆大学 机械与运载工程学院,重庆 400044; 2.重庆大学 机械传动国家重点实验室,重庆 400044; 3.航空工业直升机设计研究所,天津 333001)
直升机自诞生以来,围绕其飞行安全性、平稳性、可靠性等性能的研究就未曾停止。主减齿轮箱作为直升机重要部件之一,它的动态特性直接影响直升机飞行性能。相较于单旋翼传动系统,双旋翼共轴对转传动系统凭借具有更大的升力、更快的飞行速度等优势,已成为目前新型直升机传动系统设计聚焦的研究热点[1-2]。
围绕直升机主减齿轮传动系统动力学建模研究,郭家舜等[3]以某型直升机传动系统为研究对象,采用集中参数法建立了考虑时变啮合刚度的弯扭-耦合动力学模型,研究了三种不同飞行状态下的动态响应。Lyu等[4]针对直升机传动系统中一对直齿轮传动,采用集中参数法建立了6自由度动力学模型,分析了传动系统的动态响应。林何等[5]针对由弧齿锥齿轮和行星轮系组成的直升机传动系统为对象,研究了多种激励对传动系统动力学特性的影响。Chen等[6-7]采用集中质量法建立了直升机四级主传动系统的12自由度动力学模型,分析了关键轴扭转刚度匹配关系对系统稳定性的影响。许华超等[8]采用有限元/集中质量混合方法,建立了考虑传动轴和机匣结构柔性的直升机减速器混合动力学模型。基于超单元方法和节点有限元法,蒋函成等[9]建立了考虑轴系柔性和机匣柔性的齿轮-转子-机匣耦合系统动力学模型,研究了齿轮结果对振动能量的传递特性。
裂纹、材料剥落等齿面缺陷是高速齿轮传动经常表现出的典型疲劳失效形式。近年来,考虑齿面缺陷影响的齿轮传动系统动力学研究已经引起了广泛关注。Meng等[10]建立了引入轮齿裂纹和齿面剥落缺陷的6自由度齿轮动力学模型,研究裂纹及剥落缺陷对齿轮系统动力学的影响机理。Fan等[11]为探明直升机传动系统中行星齿轮架板裂纹对行星轮系动态特性的影响规律,建立了含裂纹并考虑多个非线性因素的直升机传动系统集中参数模型。Wan等[12]考虑齿轮副裂纹影响,建立了一对斜齿轮传动6自由度动力学模型,研究了裂纹长度对斜齿轮传动系统动态特性的影响。王鑫等[13]针对风电齿轮传动系统,建立了包含两级轴齿轮和一级行星轮的动力学模型,求解并分析了行星轮断齿时传动系统的动力学故障本质特征。Jiang等[14]建立了考虑断齿引起的质量偏心和啮合刚度影响的12自由度集中参数模型,分析了断齿对斜齿轮动态特性的影响。随后,Jiang等[15]进一步研究了三种不同尺寸裂纹的扩展对斜齿轮传动系统动态响应的影响。为了揭示裂纹故障的起源,Jiang等[16]建立了行星轮系12自由度集中参数动力学模型,对振动信号中的激励成分进行了分析。基于轴系单元法,林腾蛟等[17]建立了单级裂纹故障斜齿轮传动系统耦合动力学模型,研究了裂纹参数对系统振动响应的影响。李国彦等[18]构建了计入齿根裂纹损伤的复合行星轮系动力学模型,揭示了裂纹扩展对系统均载特性的影响。
综上所述,目前针对共轴对转齿轮箱的动力学研究较少,针对齿面缺陷的影响,大多数研究仅以单对齿轮传动为分析对象。本文针对某型无人直升机主减共轴对转齿轮箱设计,采用集中参数法建立考虑时变啮合刚度、轴承支承刚度、传动轴扭转刚度以及啮合误差等因素耦合影响的25自由度动力学模型,研究不同输入转速对各级斜齿轮动态响应的影响,分析高速级斜齿轮齿面剥落缺陷的尺度与位置变化对传动系统动态响应特性的影响规律。
1 共轴对转多级斜齿轮传动系统动力学模型
如图1所示,为直升机某型主减共轴对转斜齿轮传动系统设计方案。输入齿轮Z1与齿轮Z2和Z3同时啮合,齿轮Z2与齿轮Z4啮合。齿轮Z3与齿轮Z5构成双联齿轮,齿轮Z4与齿轮Z6构成双联齿轮。齿轮Z5和齿轮Z6分别与齿轮Z7和齿轮Z8啮合,功率由下旋翼齿轮Z7和上旋翼齿轮Z8所在的回转轴输出。采用此种传动方案,将功率经两条路径传递至两个输出端,从而驱动两主旋翼轴对转。
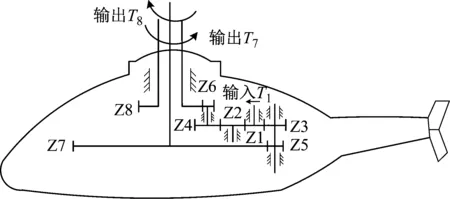
图1 直升机共轴对转多级斜齿轮传动系统简图Fig.1 Schematic diagram of coaxial contra-rotating multi-stage helical gear train for helicopters
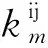
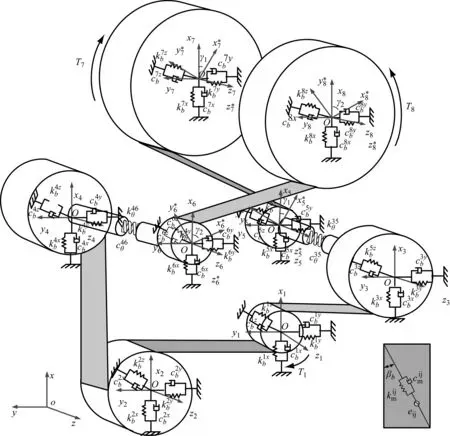
图2 共轴对转多级斜齿轮传动系统动力学模型Fig.2 Dynamic model for the coaxial contra-rotating multi-stage helical gear transmission
2 共轴对转多级斜齿轮传动系统动力学微分方程
在系统动力学模型中,各齿轮动力学方程如下所示。输入斜齿轮Z1扭转与平移动力学微分方程为
(1)
斜齿轮Z2扭转与平移动力学微分方程为
(2)
斜齿轮Z3与斜齿轮Z5扭转与平移动力学微分方程为
Fm57cos(βb)cos(γ1)=0
(3)
同理,斜齿轮Z4与斜齿轮Z6扭转与平移动力学微分方程为
Fm68cos(βb)cos(γ2)=0
(4)
斜齿轮Z7扭转与平移动力学微分方程为
(5)
斜齿轮Z8扭转与平移动力学微分方程为
(6)
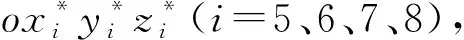
各对斜齿轮副动态啮合力分别为Fmij(i为主动轮,j为从动轮),可由式(7)~(11)计算得出。啮合误差简化为正弦函数,表示为:e(t)=Esin(ωet+φe)。E为齿轮啮合误差的幅值,φe为初始相位角,ωe为啮合频率。
Fm12,Fm13和Fm24分别为齿轮啮合副Z1-Z2、齿轮啮合副Z1-Z3以及齿轮啮合副Z2-Z4的动态啮合力。根据这三对斜齿轮副所建立的坐标系,动态啮合力计算公式如下
对于斜齿轮副Z5-Z7和Z6-Z8动态啮合力在局部坐标系中计算方式如下
其中,局部坐标系中位移值可由全局坐标系的位移值采用坐标变换的方式得到
(12)
(13)
上述所建立的动力学方程中存在刚体位移,为了动力学模型在数值求解过程中更容易收敛,需要消除其中的刚体位移。将各齿轮间的相对位移作为新的坐标,相互啮合的两齿轮取啮合线的相对位移作为新坐标,同轴的双联齿轮取等效相对位移作为新坐标。
δ35=r35(θ3-θ5)
δ46=r46(θ4-θ6)
(14)
式中,r35和r46分别为两双联齿轮的传动轴的等效半径。将式(1)~(6)化简后与式(13)合并,即可得到消除刚体位移的动力学方程
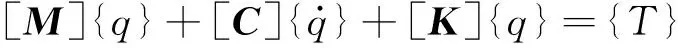
(15)
式中:[M]、[C]以及[K]分别为消除刚体位移之后的系统质量矩阵、系统阻尼矩阵和系统刚度矩阵;{q}和{T}分别是系统消除刚体位移后的位移向量和力矩向量。
3 含齿面剥落缺陷的斜齿轮啮合刚度建模
3.1 标准齿面斜齿轮啮合刚度
齿轮刚度建模经常采用的方法有能量法和石川法。其中,能量法因具有方法成熟,计算方便等优点,被广泛使用。斜齿轮啮合刚度是在直齿轮啮合刚度计算方法基础上演化而来的。Ma等[19]将直齿轮等效为悬臂梁,采用能量法计算了直齿轮时变啮合刚度。将啮合轮齿系统的总势能视为由四个部分组成:赫兹接触能量Uh,弯曲能量Ub,轴向压缩能量Ua以及剪切能量Us。各部分能量分别用来计算赫兹接触刚度kh,弯曲刚度kb,轴向压缩刚度ka和剪切刚度ks,可表示为
(16)
(17)
(18)
(19)
由于齿轮基体变形将影响其啮合线上的等效刚度,齿轮基体变形刚度不可忽略。文献[20]提出了一种计算齿轮基体变形刚度的具体计算方法
(20)
式中,系数L*,M*,P*,Q*可以采用以下多项式计算
(21)
综上所述,直齿轮总啮合刚度可由各部分刚度并联得到,计算方式如下
(22)
式(20)中,1和2分别代表主动轮与从动轮,N为某一时刻同时参与啮合轮齿的个数。
斜齿轮的结构与啮合方式都与直齿轮有着显著的区别。将斜齿轮沿着齿宽方向将轮齿切分为若干个直齿轮,斜齿轮时变啮合刚度计算方式如下[21]
(23)
(24)
(25)
式中:N为斜齿轮被切分成薄直齿轮的份数;N=round(L/Δy)(round为四舍五入取整函数,L为接触线的长度,Δy为薄直齿轮宽度)。
现共轴对转传动系统由八个斜齿轮构成,共组成5对啮合斜齿轮副,具体参数如表1所示。

表1 共轴对转多级斜齿轮传动系统参数Tab.1 Parameters of the coaxial contra-rotating multi-stage helical gear train
采用上述斜齿轮时变啮合刚度计算方法,求解该传动系统中齿轮副Z1-Z2、齿轮副Z1-Z3、齿轮副Z2-Z4和齿轮副Z5-Z7(同齿轮副Z6-Z8)时变啮合刚度,计算结果分别如图3~6所示。
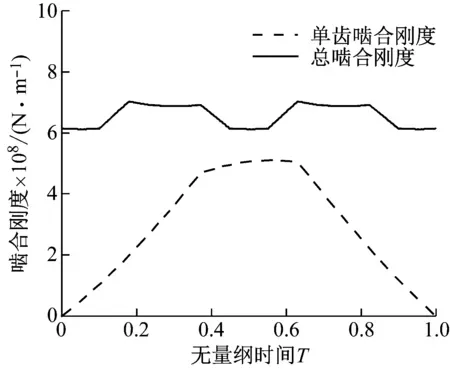
图3 齿轮副Z1-Z2时变啮合刚度Fig.3 Time-varying meshing stiffness of gear pair Z1-Z2
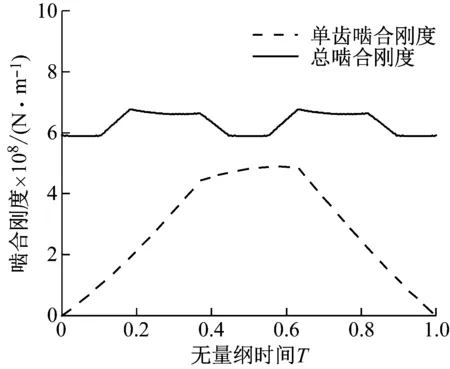
图4 齿轮副Z1-Z3时变啮合刚度Fig.4 Time-varying meshing stiffness of gear pair Z1-Z3
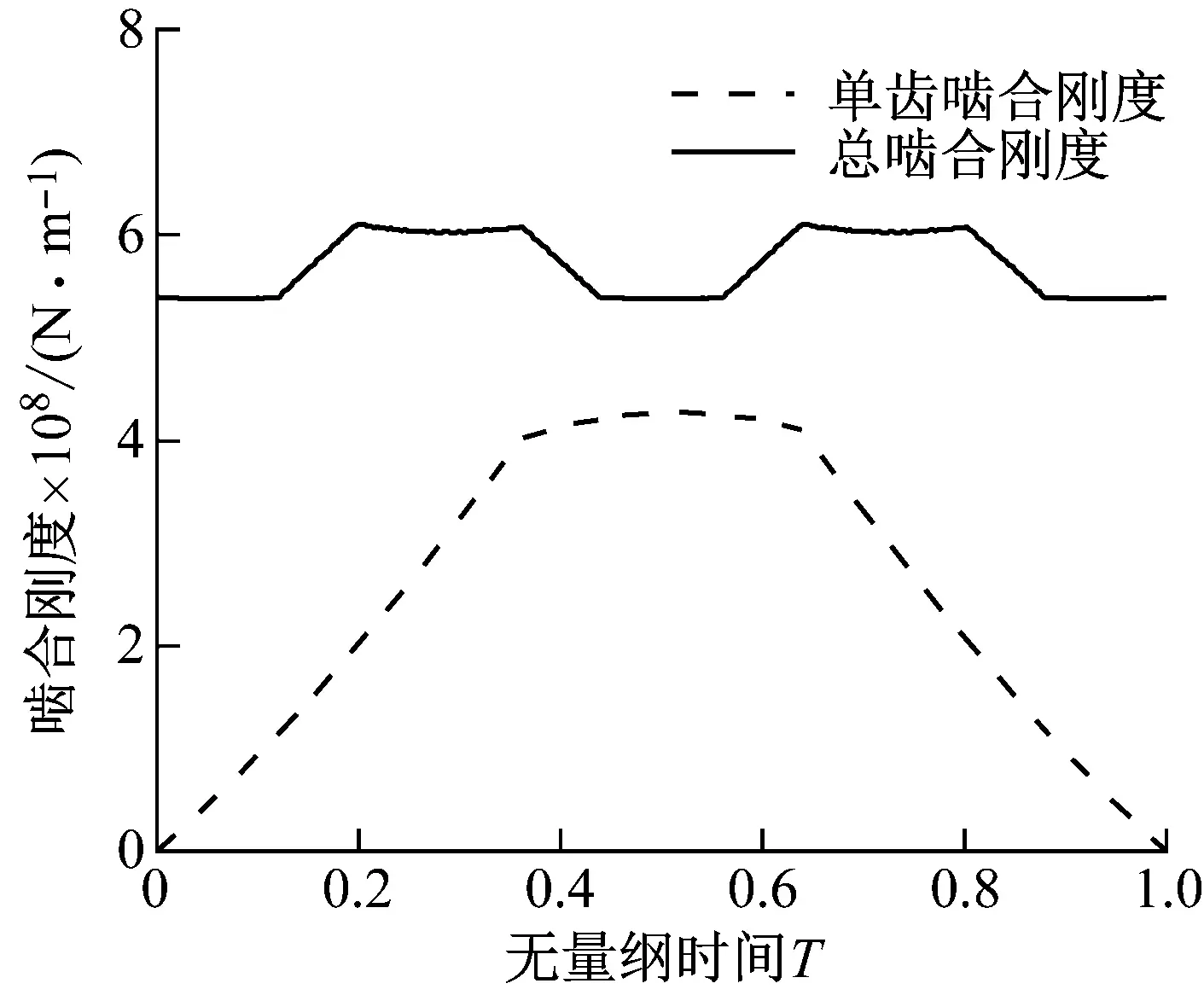
图5 齿轮副Z2-Z4时变啮合刚度Fig.5 Time-varying meshing stiffness of gear pair Z2-Z4
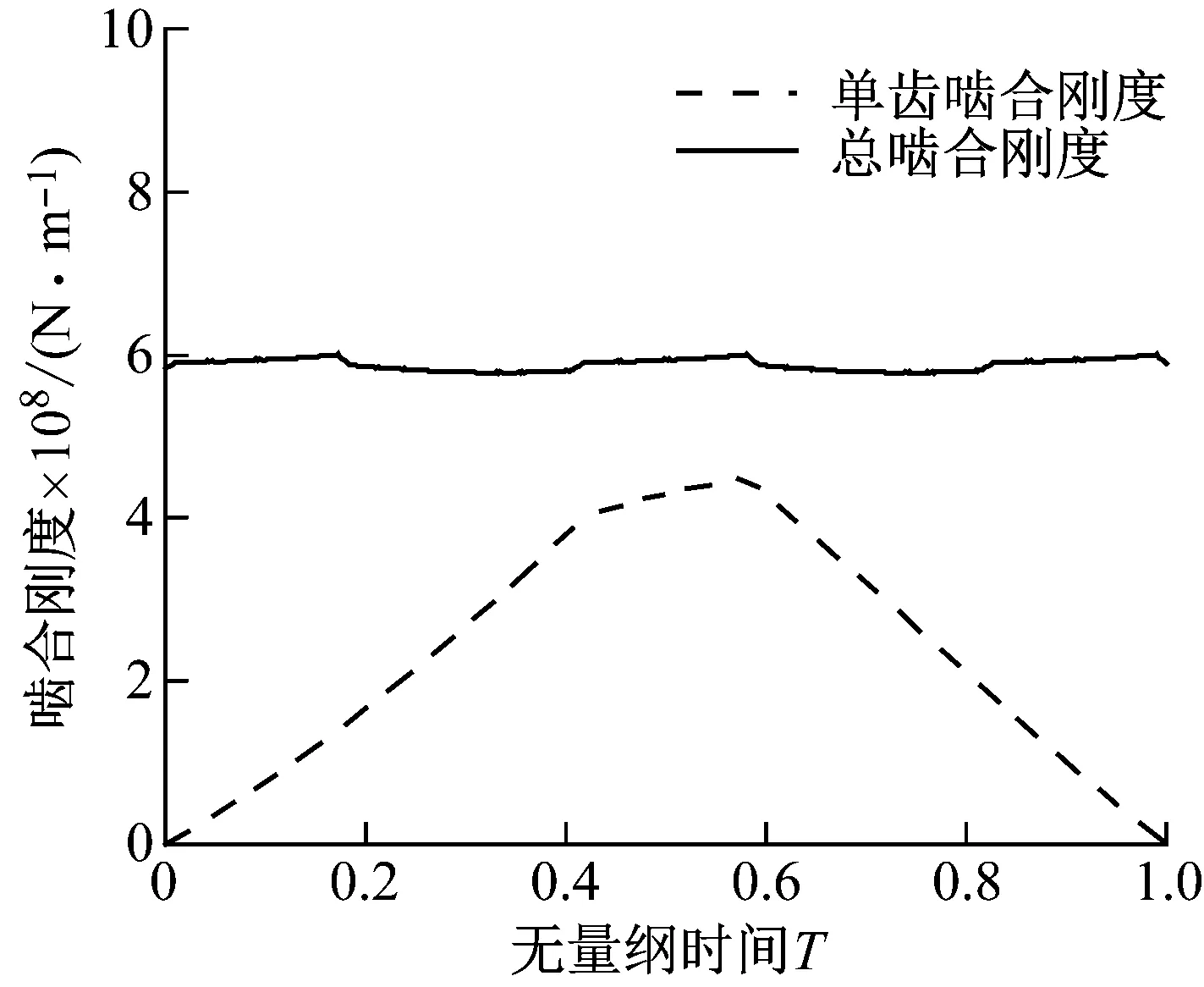
图6 齿轮副Z5-Z7(Z6-Z8)时变啮合刚度Fig.6 Time-varying meshing stiffness of gear pair Z5-Z7(Z6-Z8)
3.2 含齿面剥落缺陷斜齿轮啮合刚度
当斜齿轮齿面出现材料剥落缺陷时,啮合点到达剥落缺陷边缘就会产生较大的啮合刚度突变。可以用一个矩形槽模拟齿面剥落缺陷[22],矩形对称线平行于接触线,剥落形状的底边假设为渐开线,具体如图7所示。
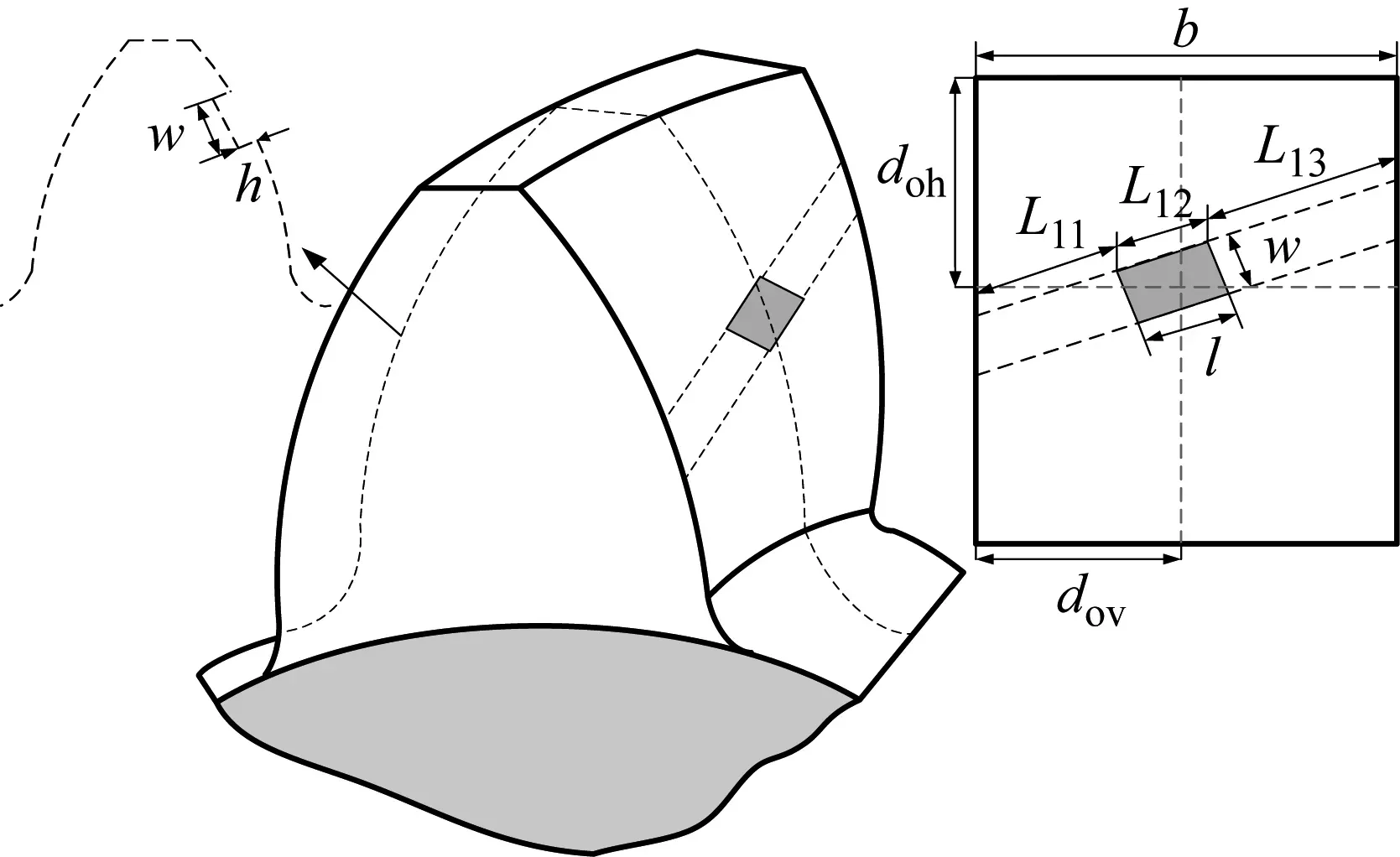
图7 斜齿轮齿面剥落缺陷模型Fig.7 Defect model of helical gear tooth surface spalling
剥落缺陷用三个维度表示:w(宽度)×l(长度)×h(高度),其中心在作用面上的位置(dov,doh)。结合切片法的思想,当接触线到达缺陷的位置时,切片后的直齿轮将被分成L11、L12和L13三部分。每部分的数量可以由下式计算得到
N11=round(L11(t)/Δy)
(26a)
N12=round(L12(t)/Δy)
(26b)
N13=round(L13(t)/Δy)
(26c)
式中,L11(t),L12(t)和L13(t)分别是被缺陷分隔出的三部分的长度。因此在剥落缺陷位置的单齿啮合刚度可表述为
(27)
啮合刚度依然由赫兹接触刚度,轴向压缩刚度,剪切刚度,弯曲刚度以及轮齿基体刚度。Han等推导了每个刚度的计算公式
弯曲刚度
(28)
其中
(29a)
(29b)
剪切刚度:
(30)
其中
(30a)
(30b)
轴向压缩刚度:
(31)
其中
(31a)
(31b)
赫兹接触刚度:
(32)
式中,αs1和αs2为缺陷位置的压力角。
基于式(20)和式(29)~(32),可以计算出含剥落缺陷斜齿轮时变啮合刚度。由于输入斜齿轮高速运转的极端工况,很容易在循环接触应力和齿面摩擦力作用下产生齿面材料剥落缺陷。因此,结合表1中斜齿轮基本参数,计算齿轮副Z1-Z2和齿轮副Z1-Z3在主动轮Z1齿面存在不同尺寸、不同位置剥落缺陷时的时变啮合刚度。图8(a)~(c)和图10(a)~(c)分别为齿轮1齿面长4 mm缺陷存在双齿啮合区、三齿啮合区以及双齿啮合区与三齿啮合区交界处三种不同位置时,齿轮副Z1-Z2和齿轮副Z1-Z3的时变啮合刚度。图9和图11分别为轮齿Z1齿面存在l=2 mm、4 mm和8 mm长度缺陷时,齿轮副Z1-Z2和齿轮副Z1-Z3的时变啮合刚度。
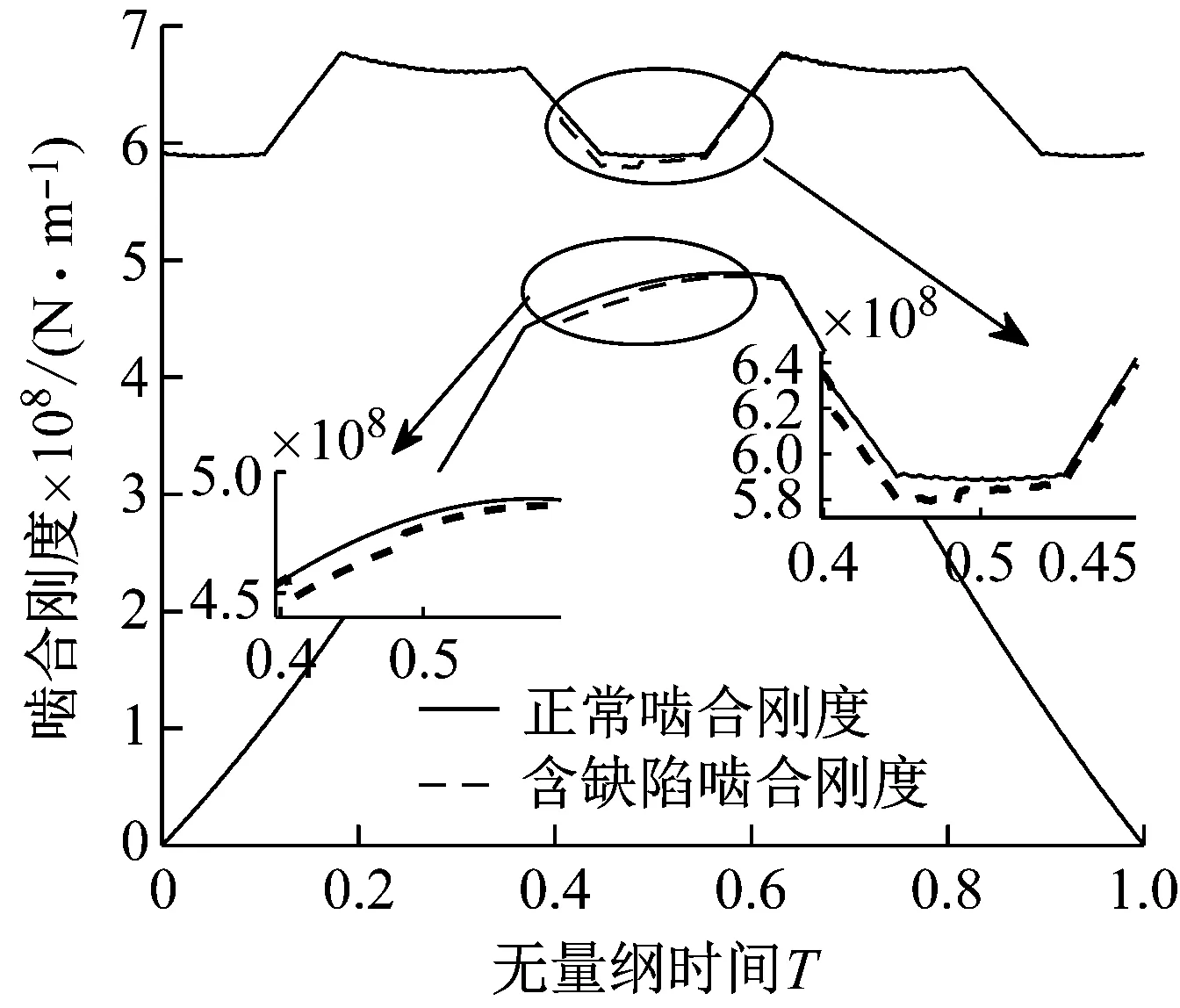
(a) 齿面双齿啮合区与三齿啮合区交界处缺陷
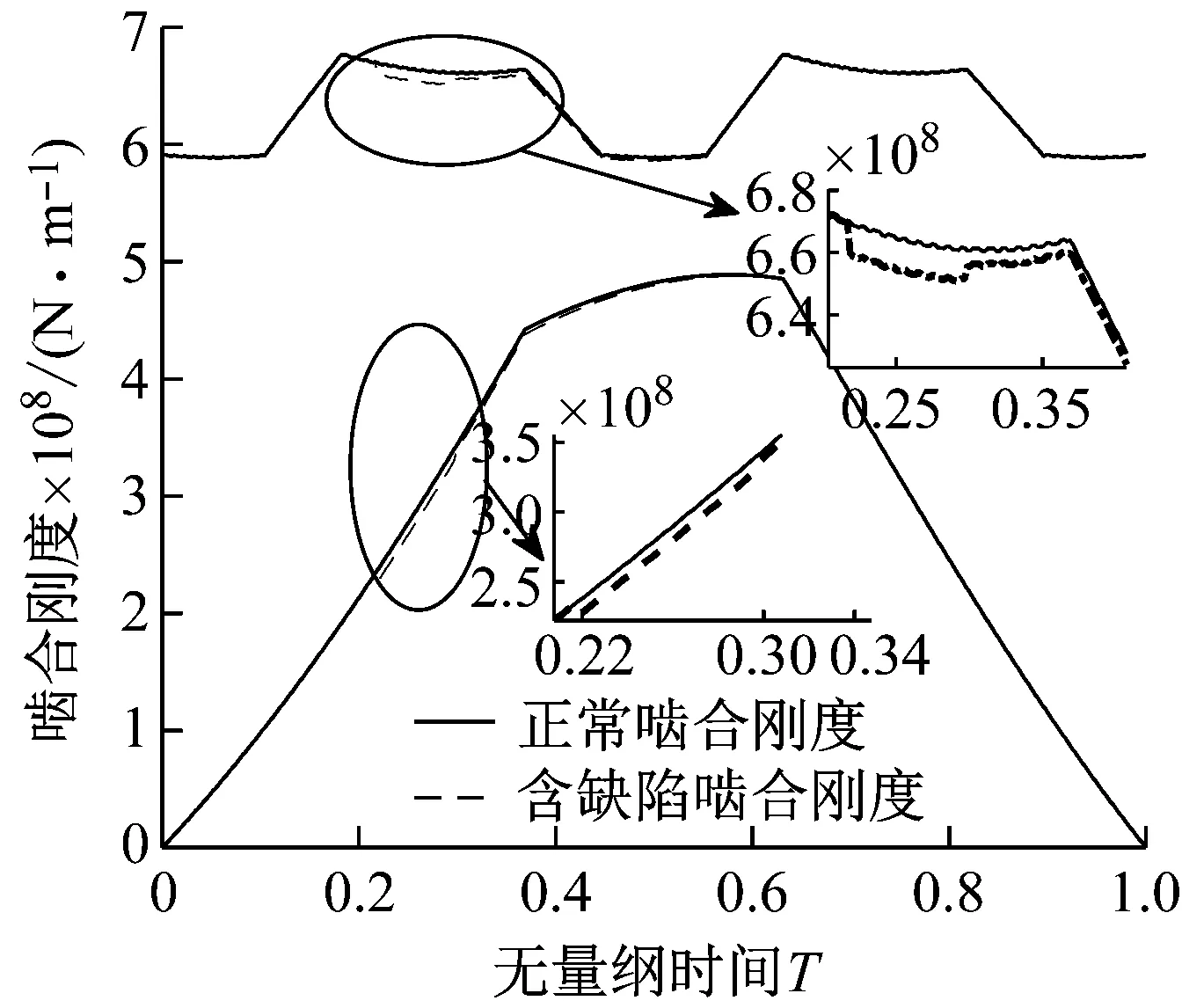
(b) 齿面三齿啮合区缺陷
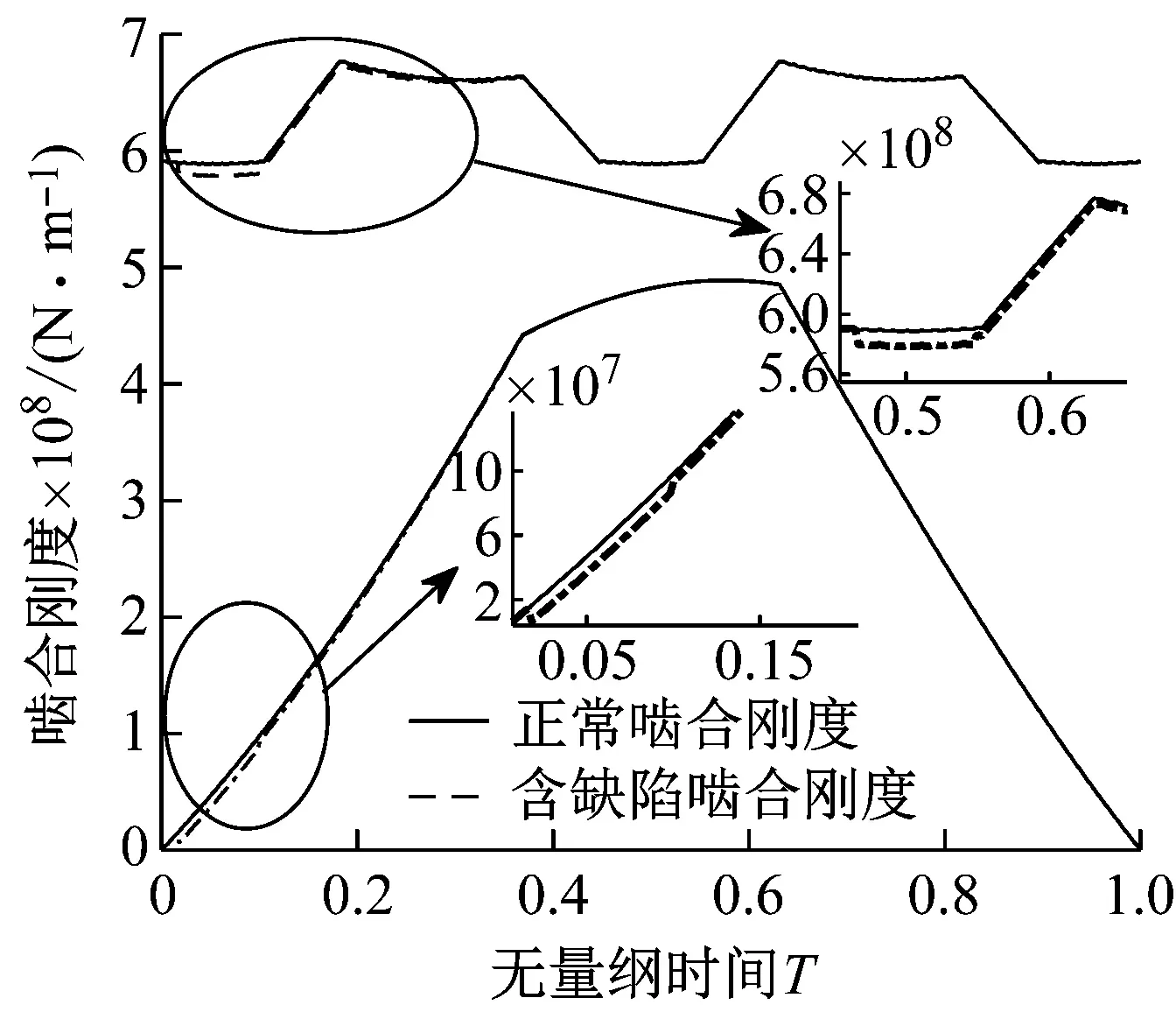
(c) 齿面双齿啮合区缺陷图8 不同缺陷位置齿轮副Z1-Z2时变啮合刚度Fig.8 Time-varying meshing stiffness of gear pairs Z1-Z2 with different defective positions
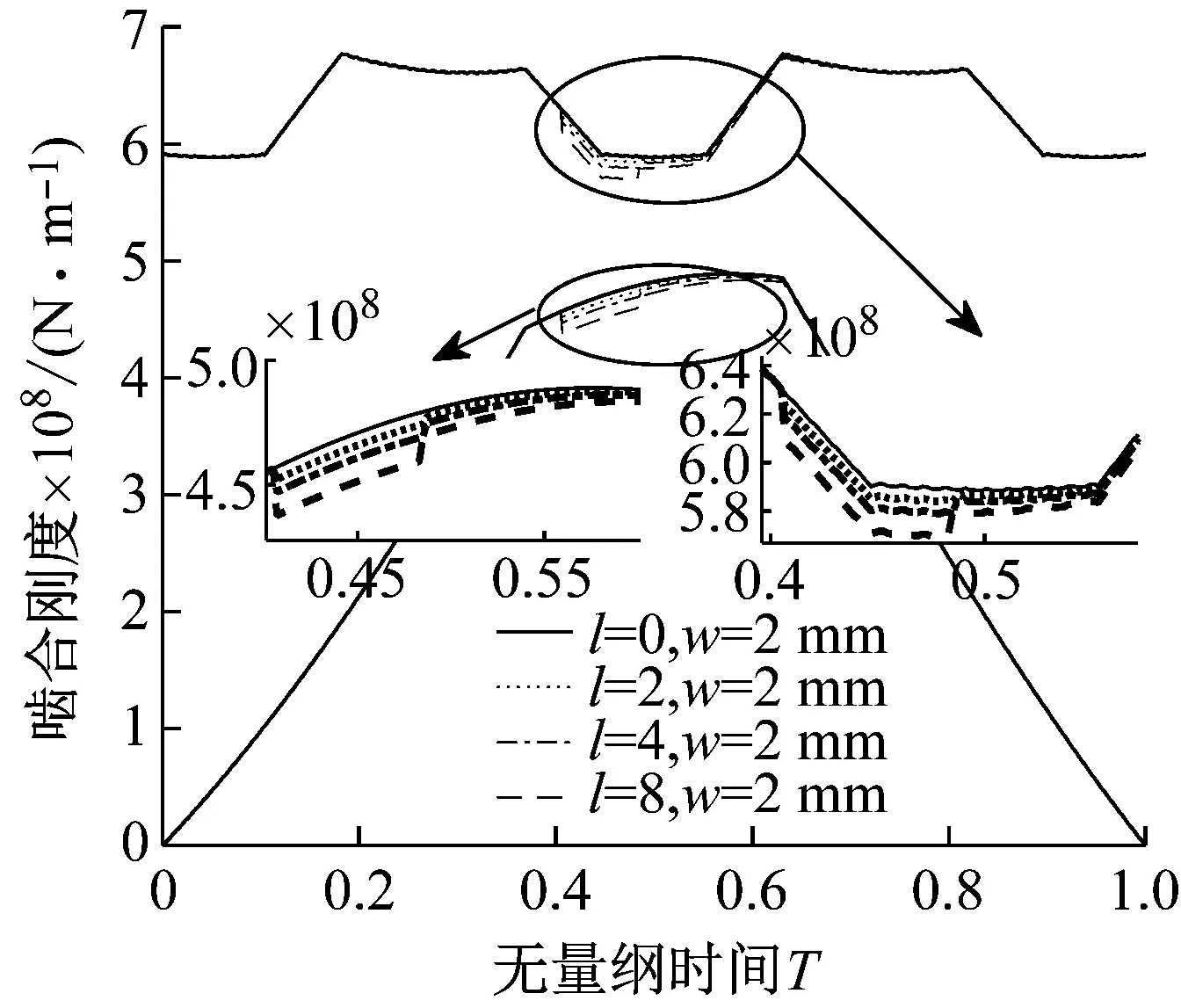
图9 不同缺陷尺寸齿轮副Z1-Z2时变啮合刚度Fig.9 Time-varying meshing stiffness of gear pairs Z1-Z2 with different defective sizes
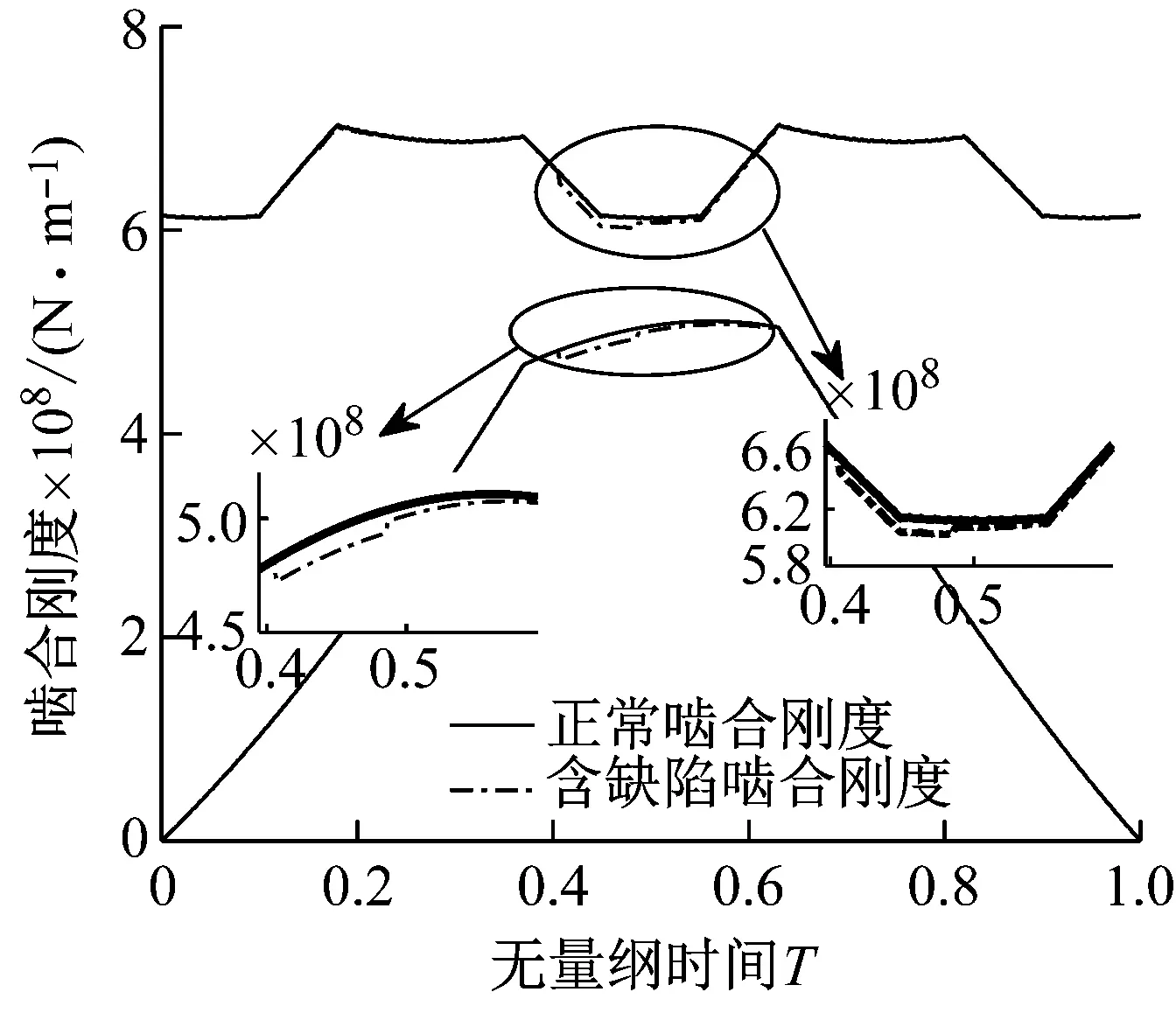
(a) 齿面双齿啮合区与三齿啮合区交界处缺陷
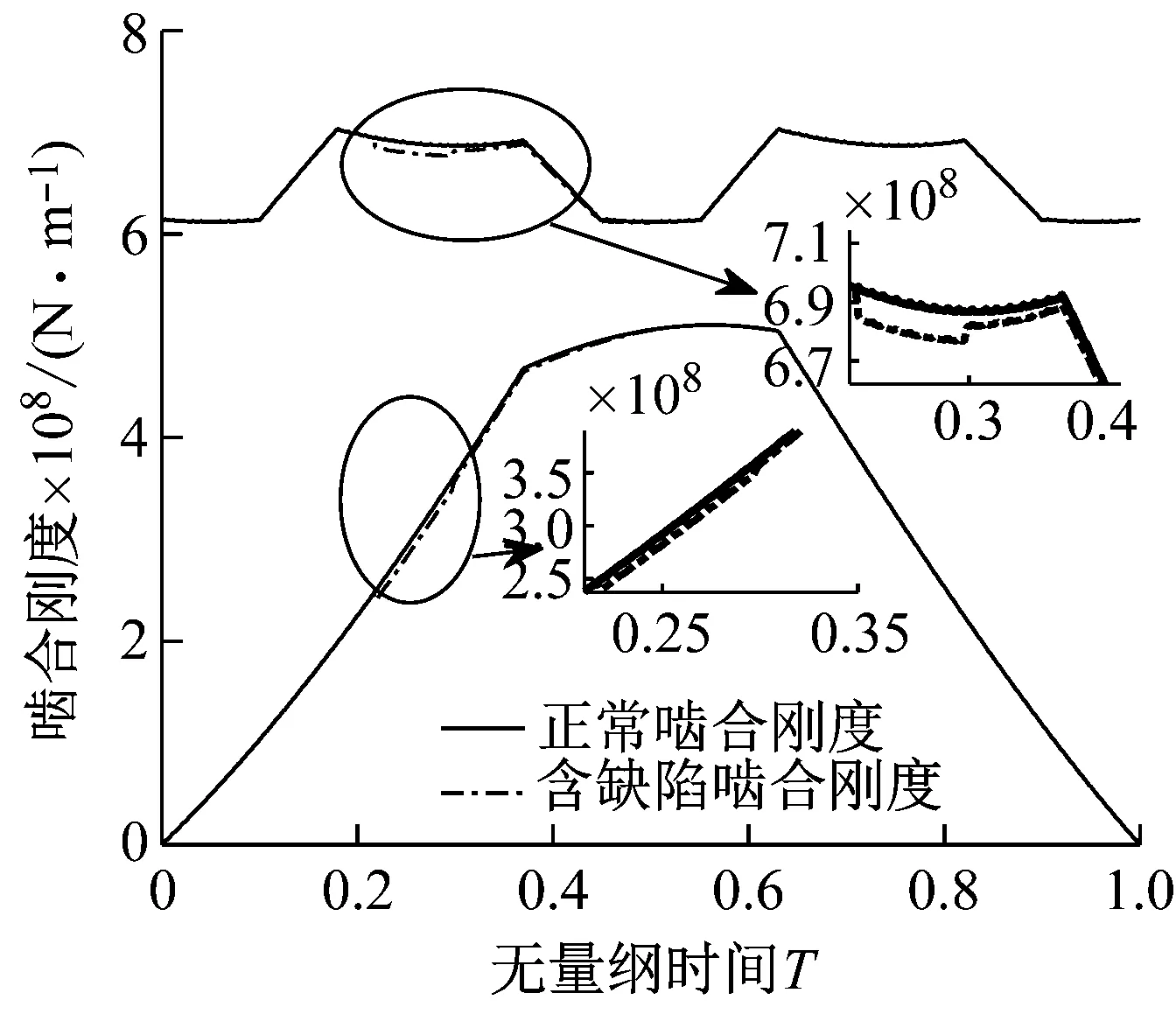
(b) 齿面三齿啮合区缺陷
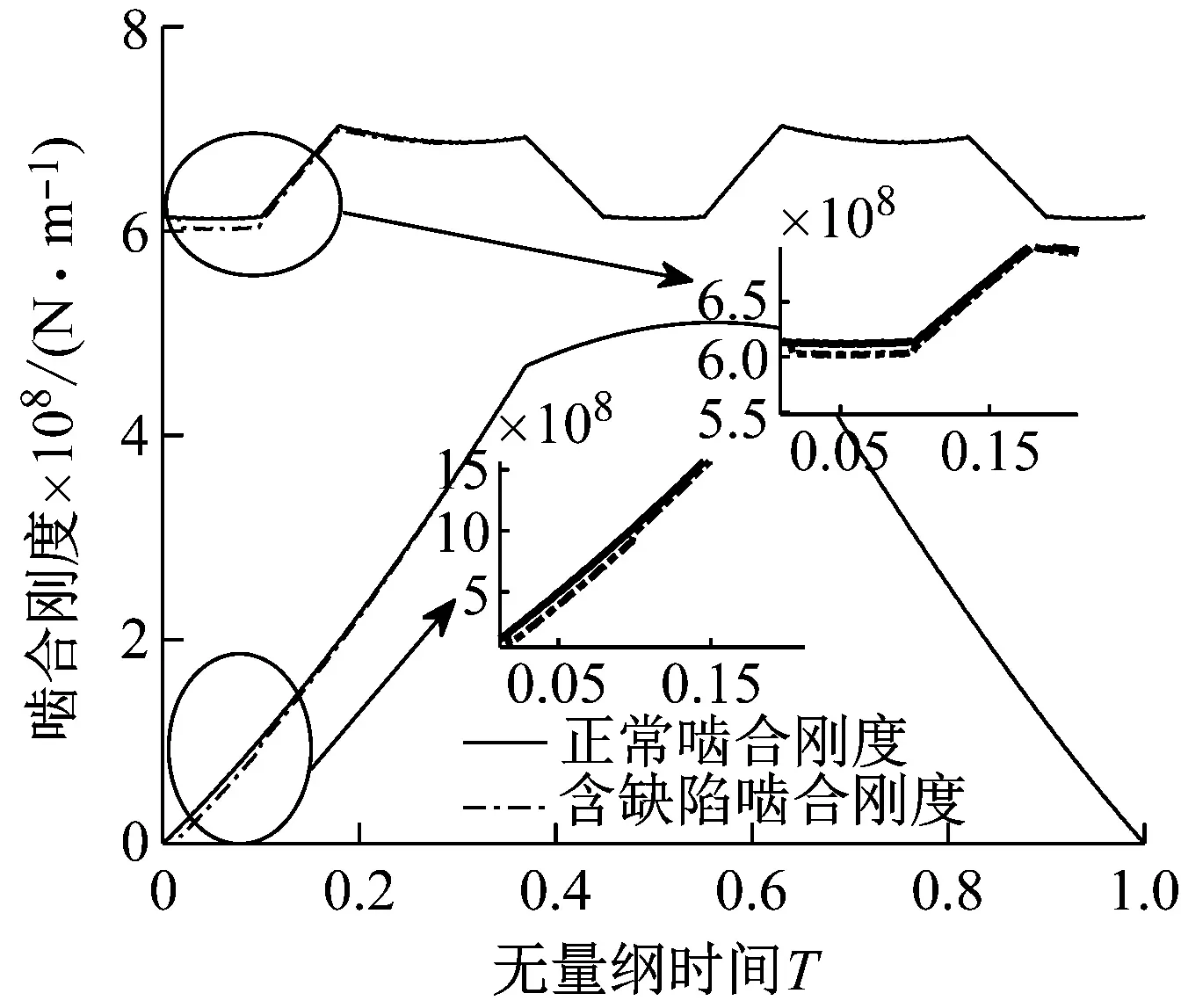
(c) 齿面双齿啮合区缺陷图10 不同缺陷位置齿轮副Z1-Z3时变啮合刚度Fig.10 Time-varying meshing stiffness of gear pairs1-3with different defective positions
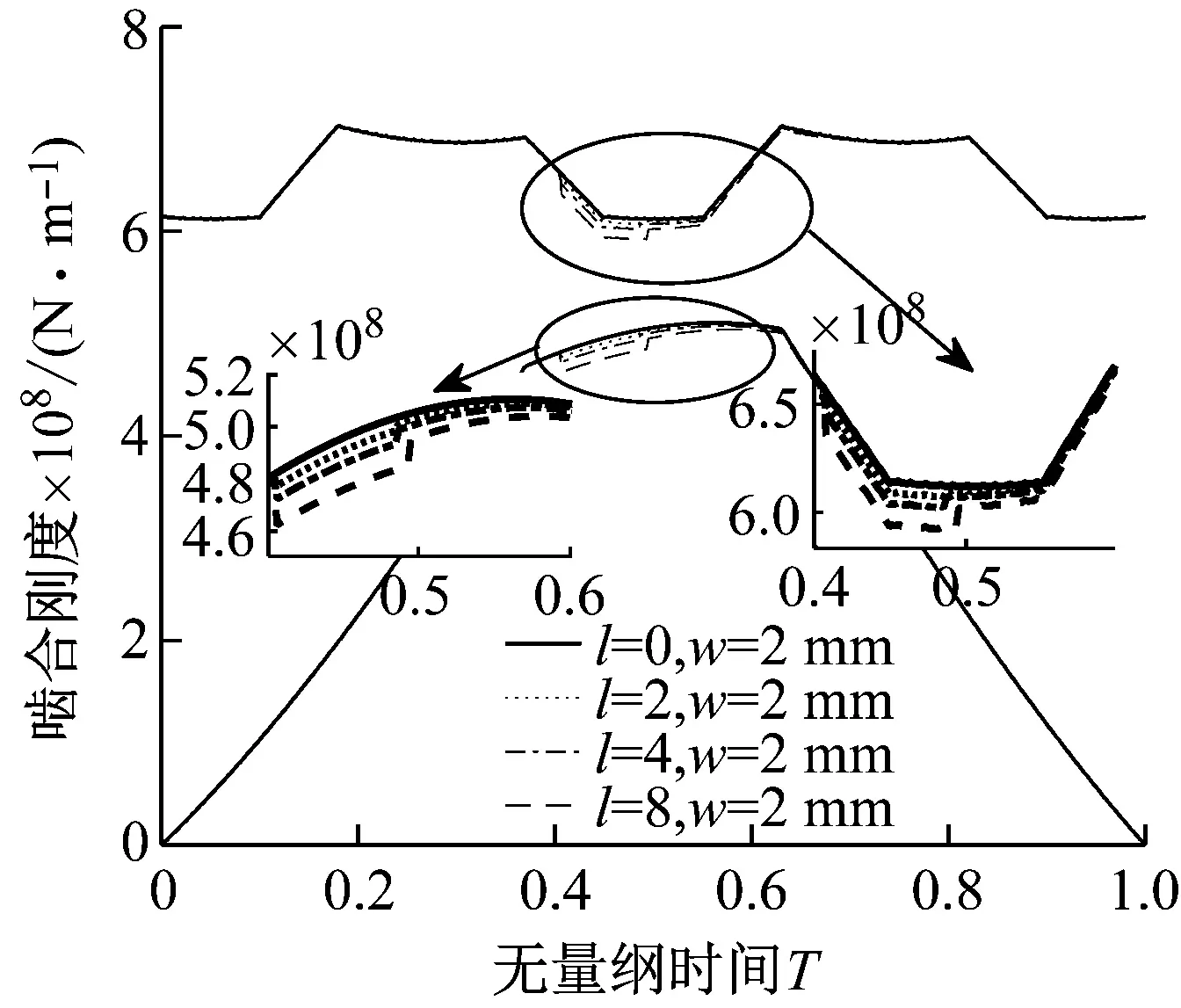
图11 不同尺寸缺陷齿轮副Z1-Z3时变啮合刚度Fig.11 Time-varying meshing stiffness of gear pairs Z1-Z3 with different defective sizes
4 共轴对转斜齿轮传动系统振动特性分析
该传动系统动力学模型拥有25个自由度,考虑了齿轮副时变啮合刚度,支承轴承刚度,传动轴的扭转刚度以及啮合误差等影响因素,是一个强非线性动力学微分方程组。将采用45阶变步长龙格库塔法对所建立的动力学模型进行数值求解,研究不同输入转速对各级斜齿轮动态响应的影响,分析高速级斜齿轮齿面剥落缺陷的尺度与位置变化对传动系统振动特性的影响规律。
4.1 定转速下斜齿轮传动系统振动特性
根据齿轮箱转速与负载工况条件,设定高速输入级齿轮转速为2 000 r/min,输入斜齿轮Z1,斜齿轮Z2,斜齿轮Z3以及斜齿轮Z4直接啮合,啮合频率相同为fm1=fm2=fm3=fm4=700 Hz,转频分别为f1=33.33 Hz,f2=16.3 Hz,f3=14 Hz,f4=14 Hz。而传动链末端斜齿轮5,6,7和8的啮合频率fm5=fm6=fm7=fm8=280 Hz,转频分别为f5=f6=14 Hz,f7=f8=2.43 Hz。求出的各个齿轮副的动态啮合力时域图与频域图,如图12~13所示。
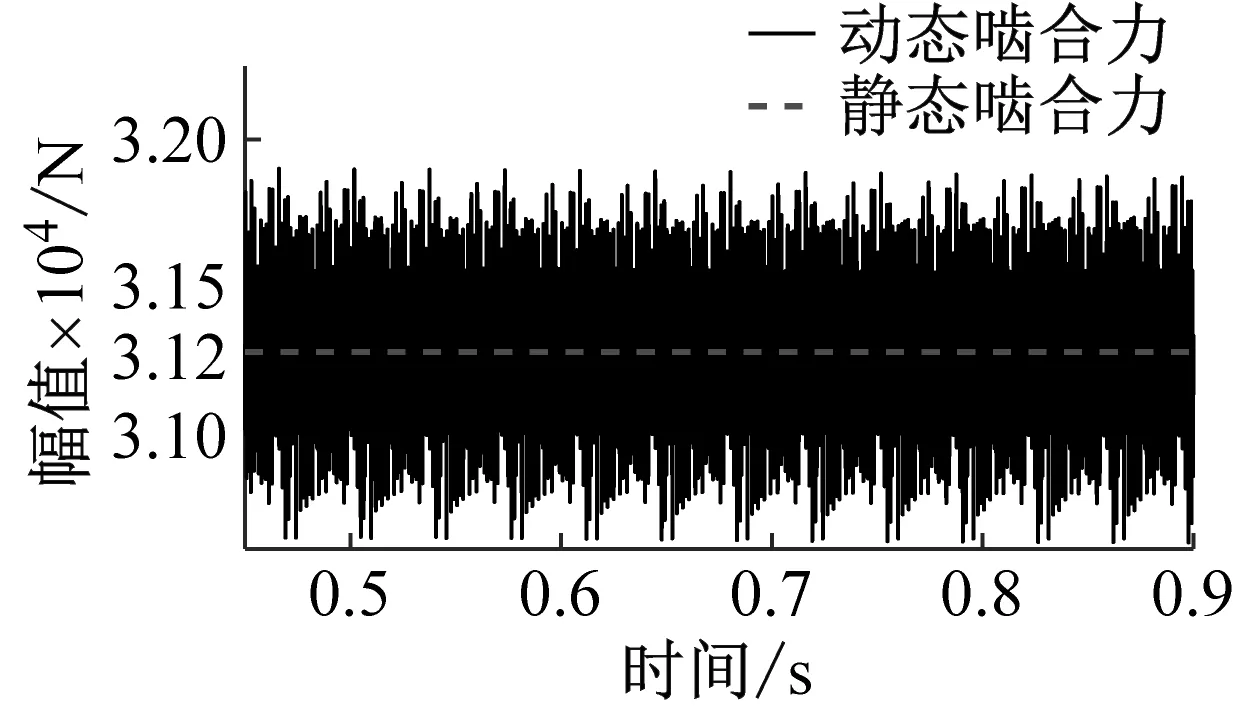
(a) 动态啮合力Fm12时域响应
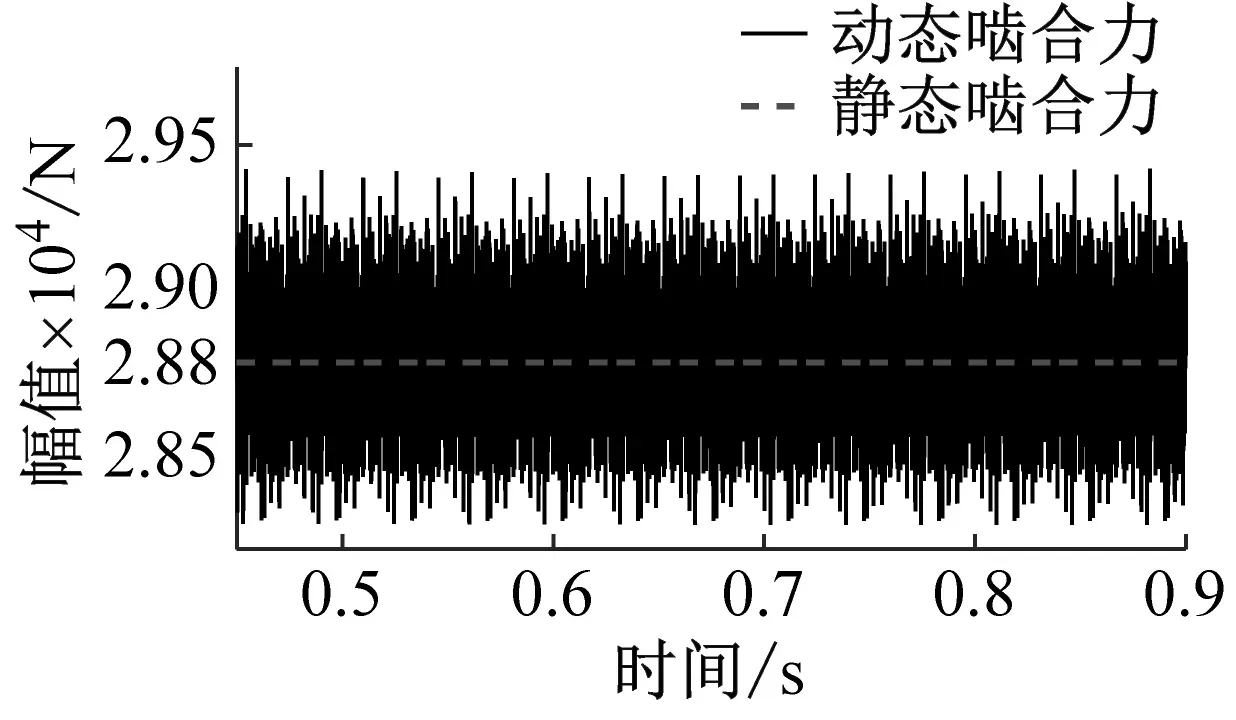
(b) 动态啮合力Fm13时域响应
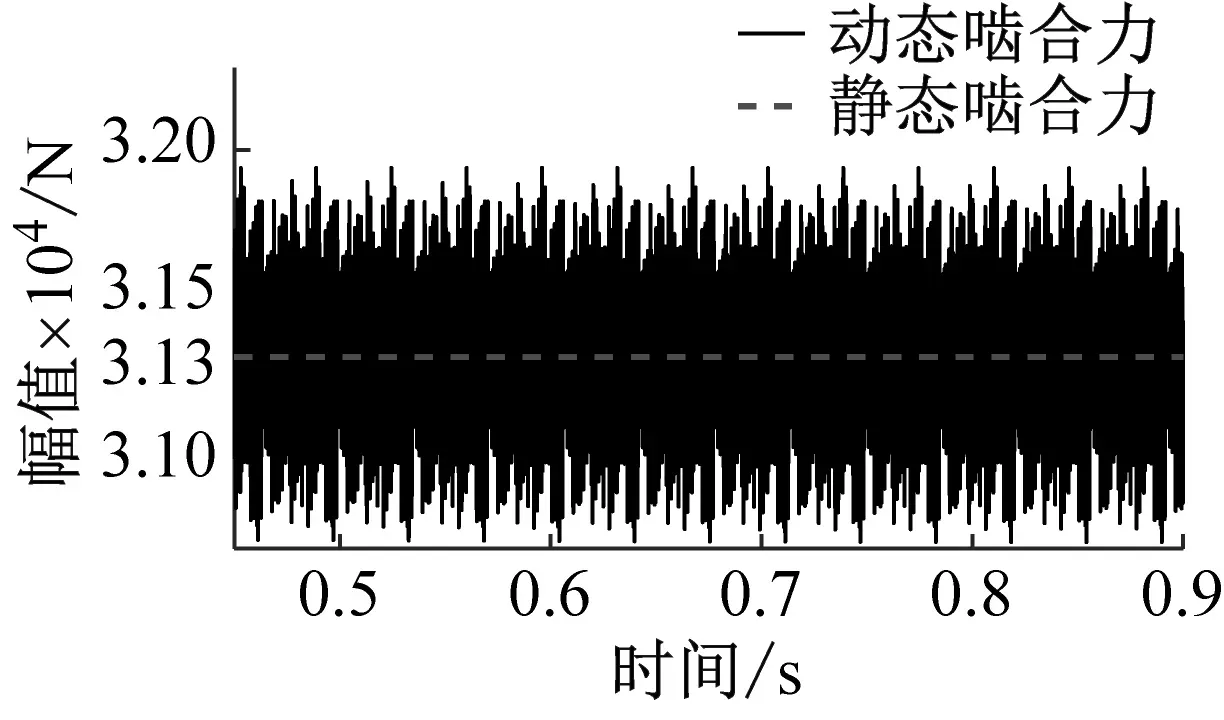
(c) 动态啮合力Fm24时域响应
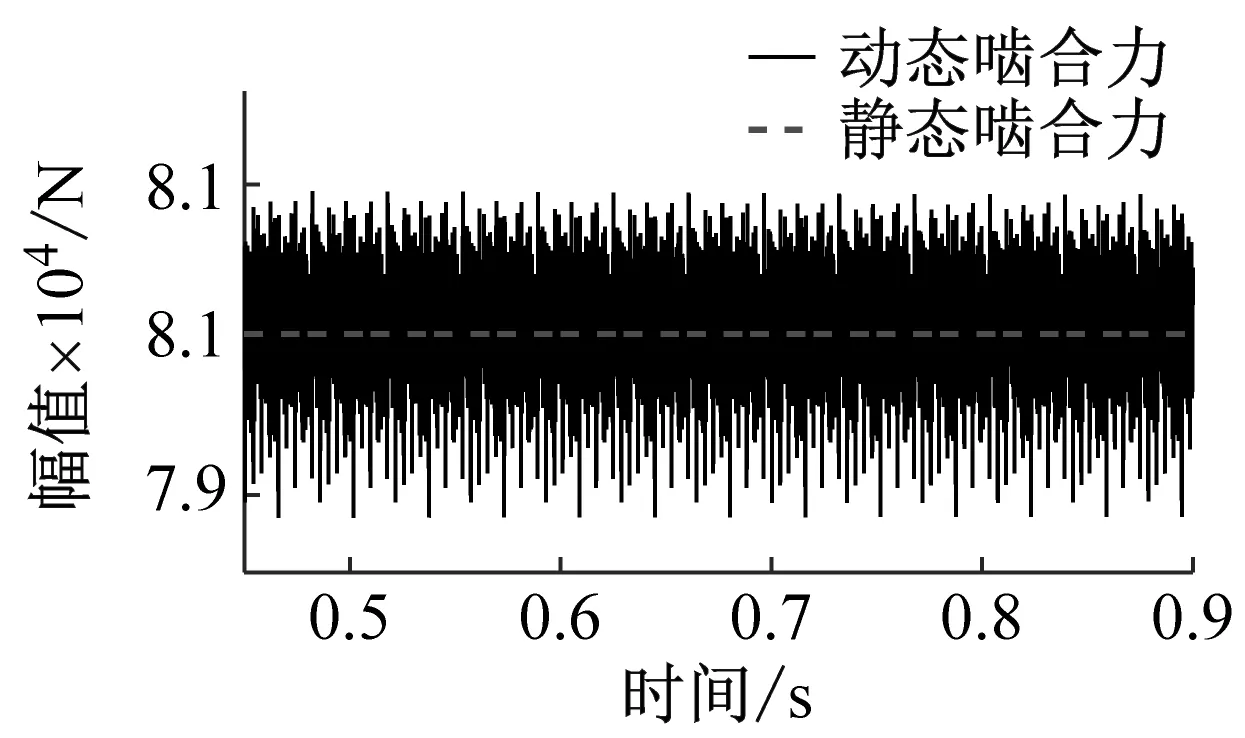
(d) 动态啮合力Fm57时域响应
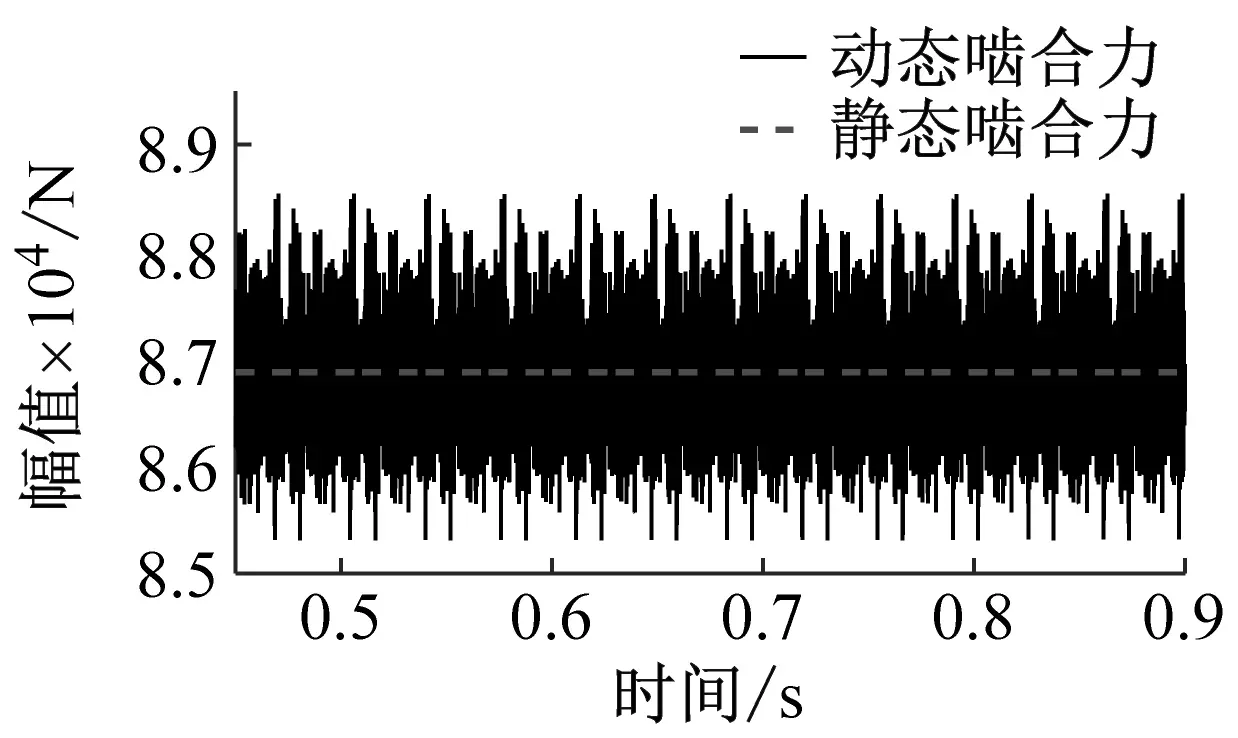
(e) 动态啮合力Fm68时域响应图12 各级齿轮副动态啮合力时域响应Fig.12 Time domain response of dynamic meshing force of gear pairs at various levels
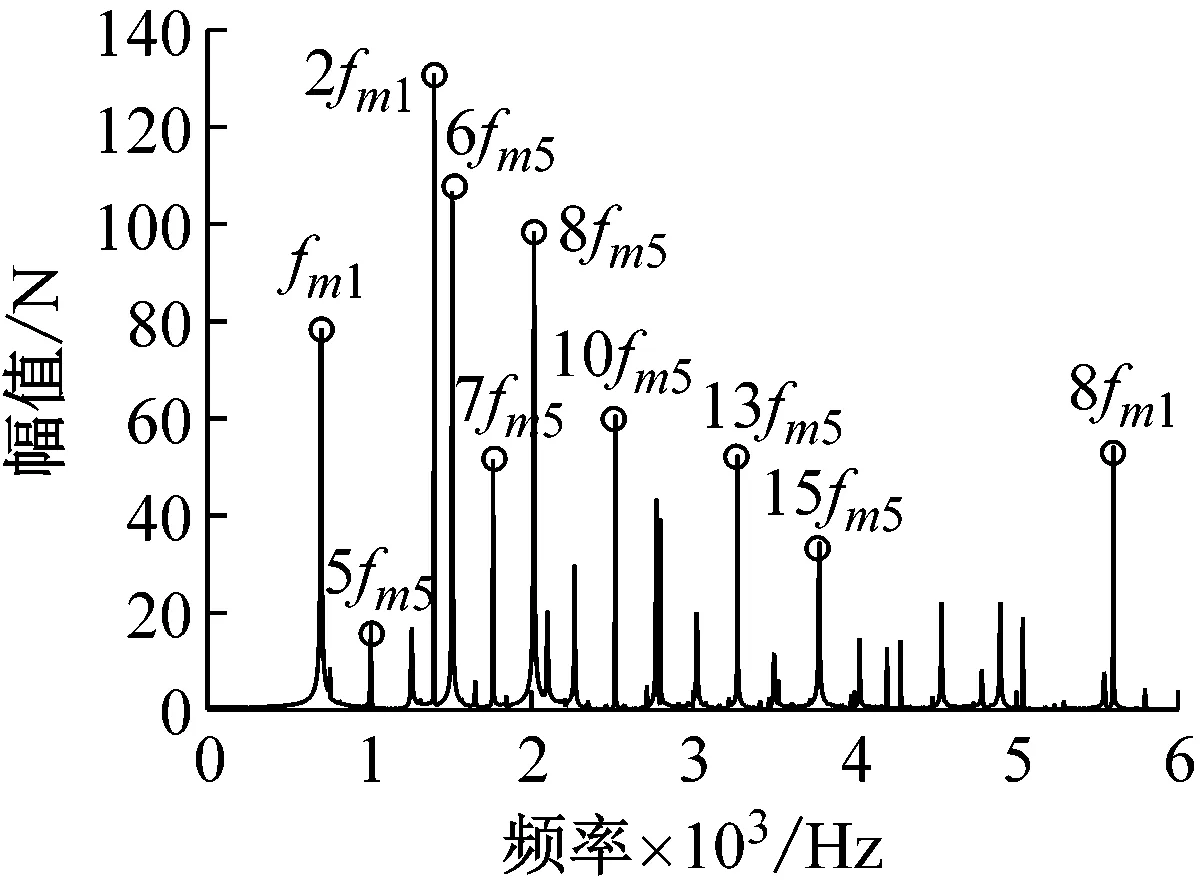
(a) 动态啮合力Fm12频域响应
(b) 动态啮合力Fm13频域响应
(c) 动态啮合力Fm24频域响应
(d) 动态啮合力Fm57频域响应
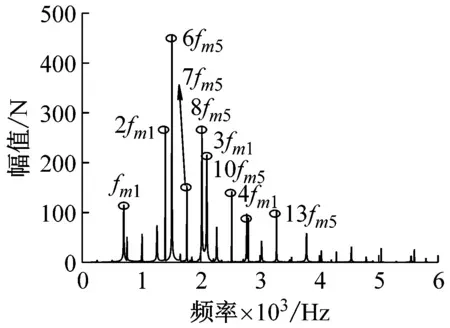
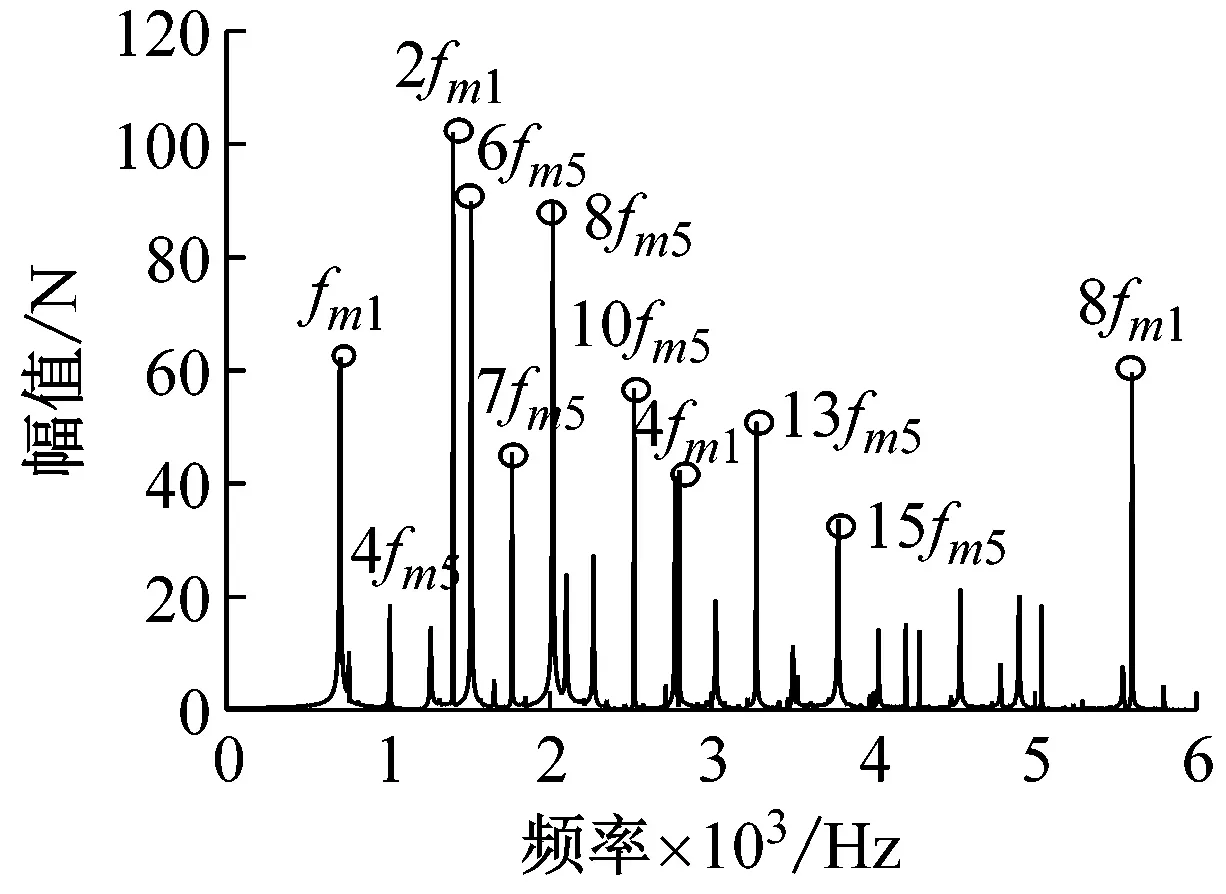
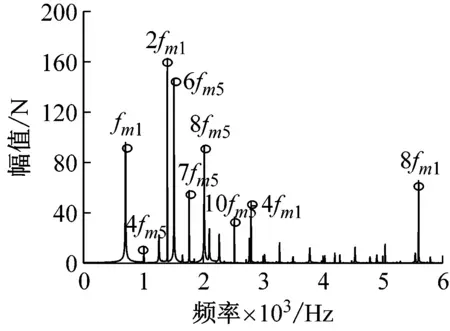
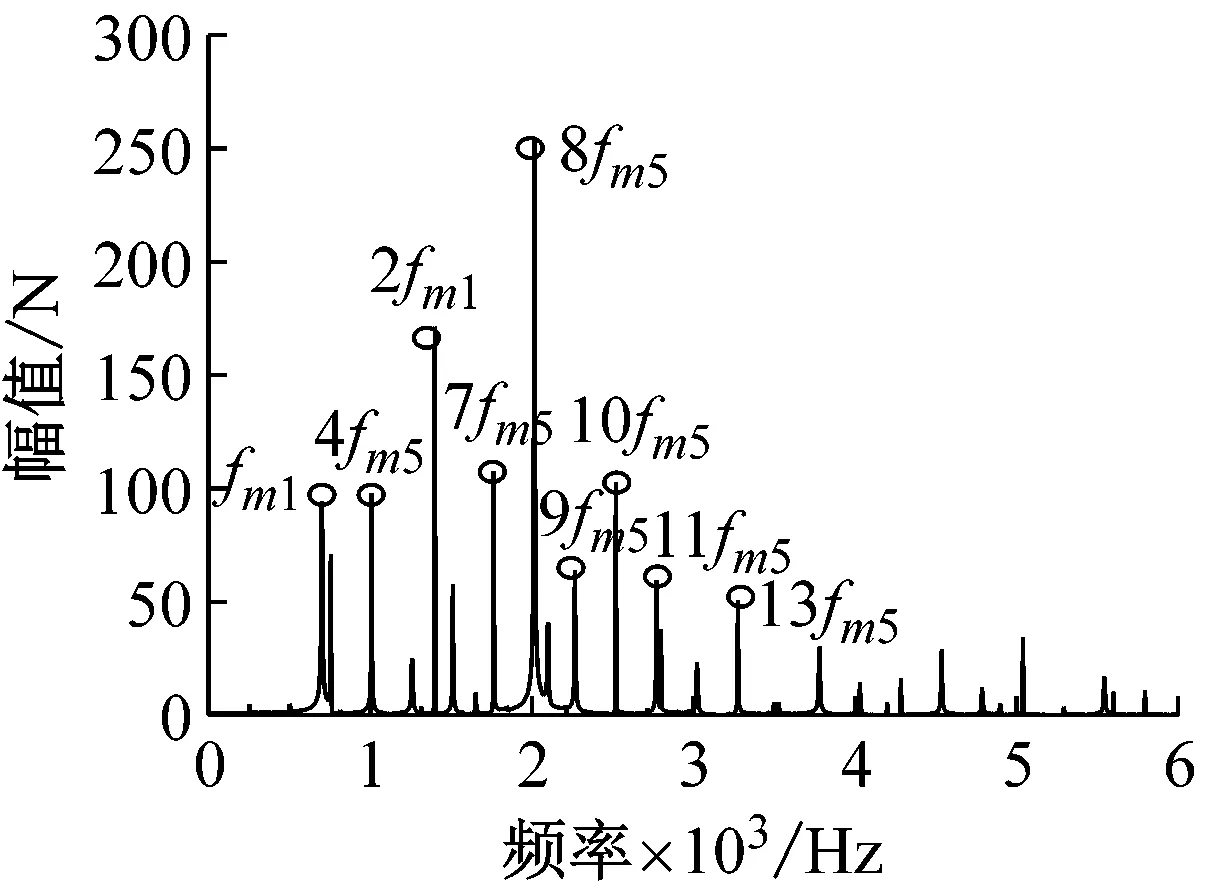
(e) 动态啮合力Fm68频域响应图13 各级齿轮副动态啮合力频域响应Fig.13 Frequency domain response of dynamic meshing force of gear pairs at various levels
在时域响应中,各级齿轮副动态啮合力围绕理论静态啮合力上下波动,并呈现周期性。通过理论计算斜齿轮副Z1-Z2、斜齿轮副Z1-Z3、斜齿轮副Z2-Z4、斜齿轮副Z5-Z7和斜齿轮副Z6-Z8的静态啮合力分别为31 270 N,28 770 N,31 270 N,80 037 N,86 876 N。利用均方根差(RMSE)指标评价各齿轮副动态啮合力波动程度。各齿轮副动态啮合力的均方根差依次为206.5,186.7,228.4,330.5,583.4。可以看出两驱动旋翼轴齿轮副的动态啮合力波动程度较大,且上旋翼驱动斜齿轮副Z6-Z8的动态啮合力波动程度最大,是下旋翼驱动斜齿轮副Z5-Z7的1.7倍。
对时域信号去除直流分量,做FFT变换,得到各齿轮副动态啮合力频域响应。在频域响应中,可以观察出幅值较高的峰对应的频率成分都是啮合频率及其倍频。图13(a)斜齿轮副Z1-Z2的动态啮合力频率响应在2fm1频率处幅值最大,在此之后的高频部分幅值较大的皆为fm5倍频。齿轮Z1~Z4处于相互啮合传动链上,齿轮副Z1-Z2、Z1-Z3和Z2-Z4的频域响应较为相似,幅值最大也在2fm1频率处,只是幅值大小不同,如图13(a)~(c)。输出旋翼端斜齿轮副通过传动轴与上述啮合传动链相连,频域相差较大。图13(d)为齿轮啮合副Z5-Z7的频域图,在频率8fm5处幅值最大,2fm1频率处次之。然而在齿轮啮合副Z6-Z8的频域图中,频率5fm5(5fm6)处的幅值最大。
4.2 不同输入转速对传动系统振动特性的影响
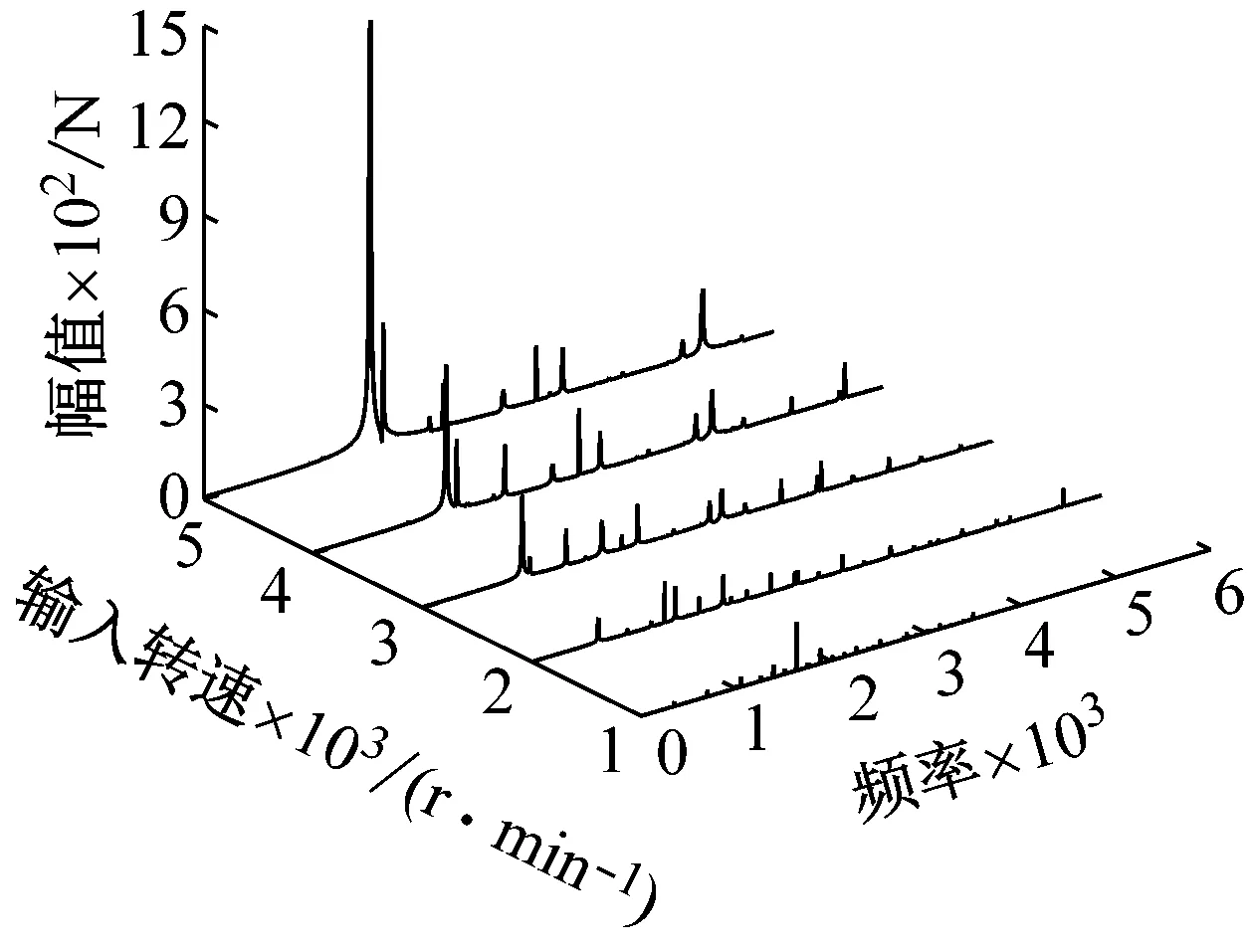
将输入转速分别设定为1 000 r/min、2 000 r/min、3 000 r/min、4 000 r/min和5 000 r/min。求解动力学模型,得出各级齿轮副动态啮合力在不同转速下的动态响应。如图14所示,为不同输入转速下各级齿轮副动态啮合力对比。
(a) 不同输入转速下动态啮合力Fm12频域响应
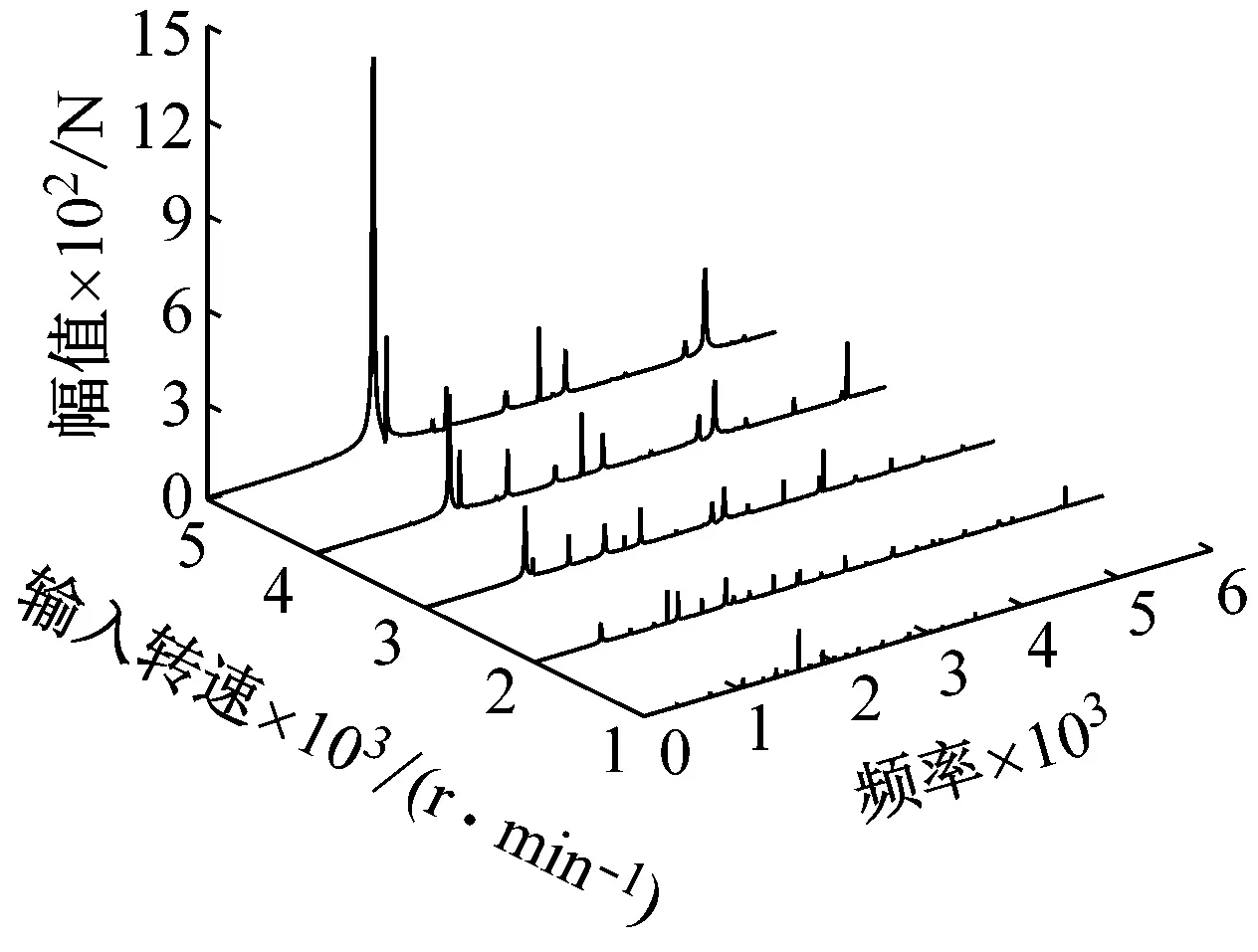
(b) 不同输入转速下动态啮合力Fm13频域响应
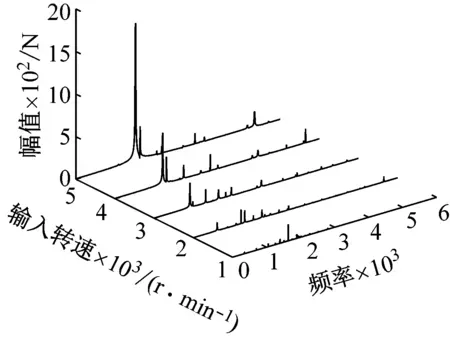
(c) 不同输入转速下动态啮合力Fm24频域响应
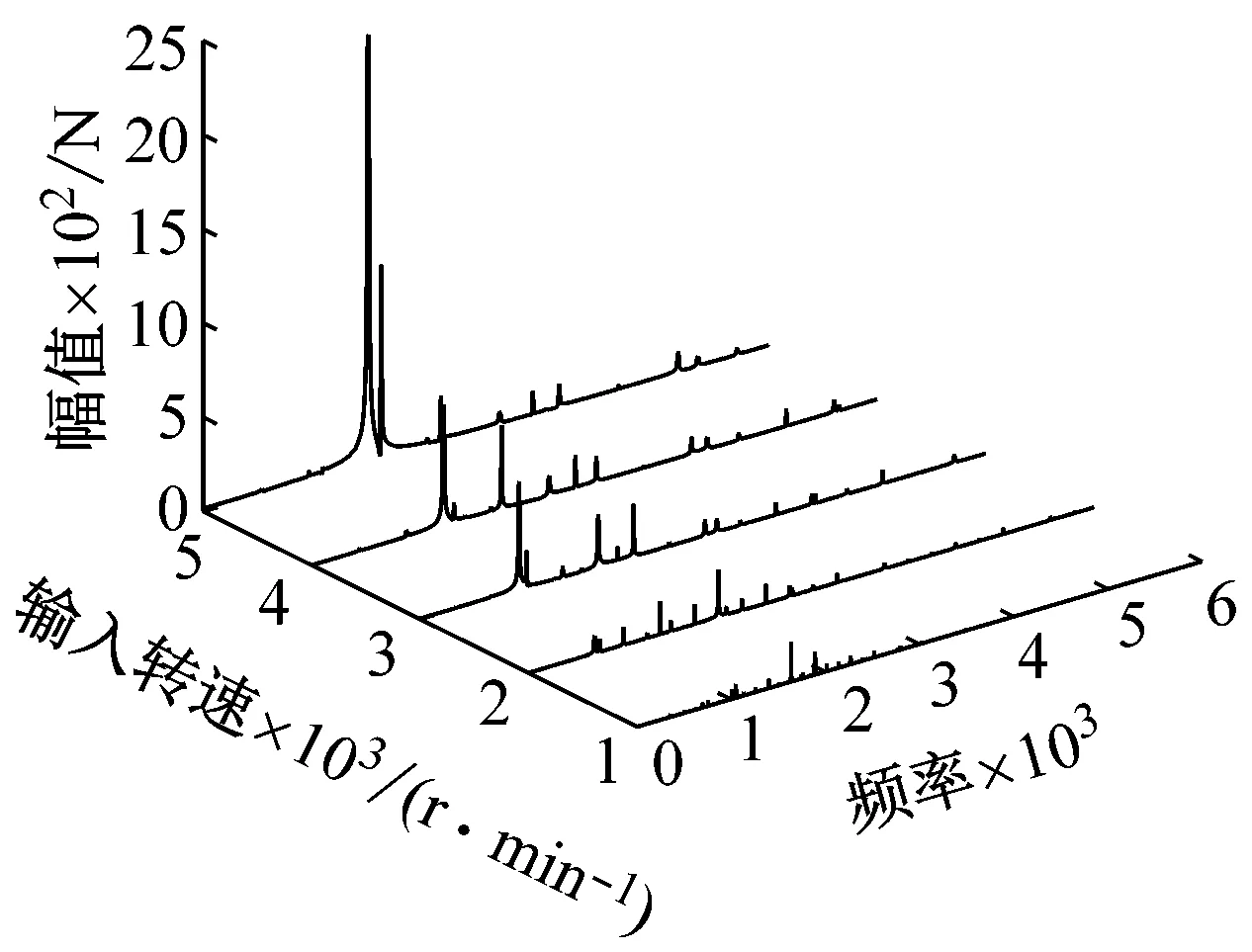
(d) 不同输入转速下动态啮合力Fm57频域响应
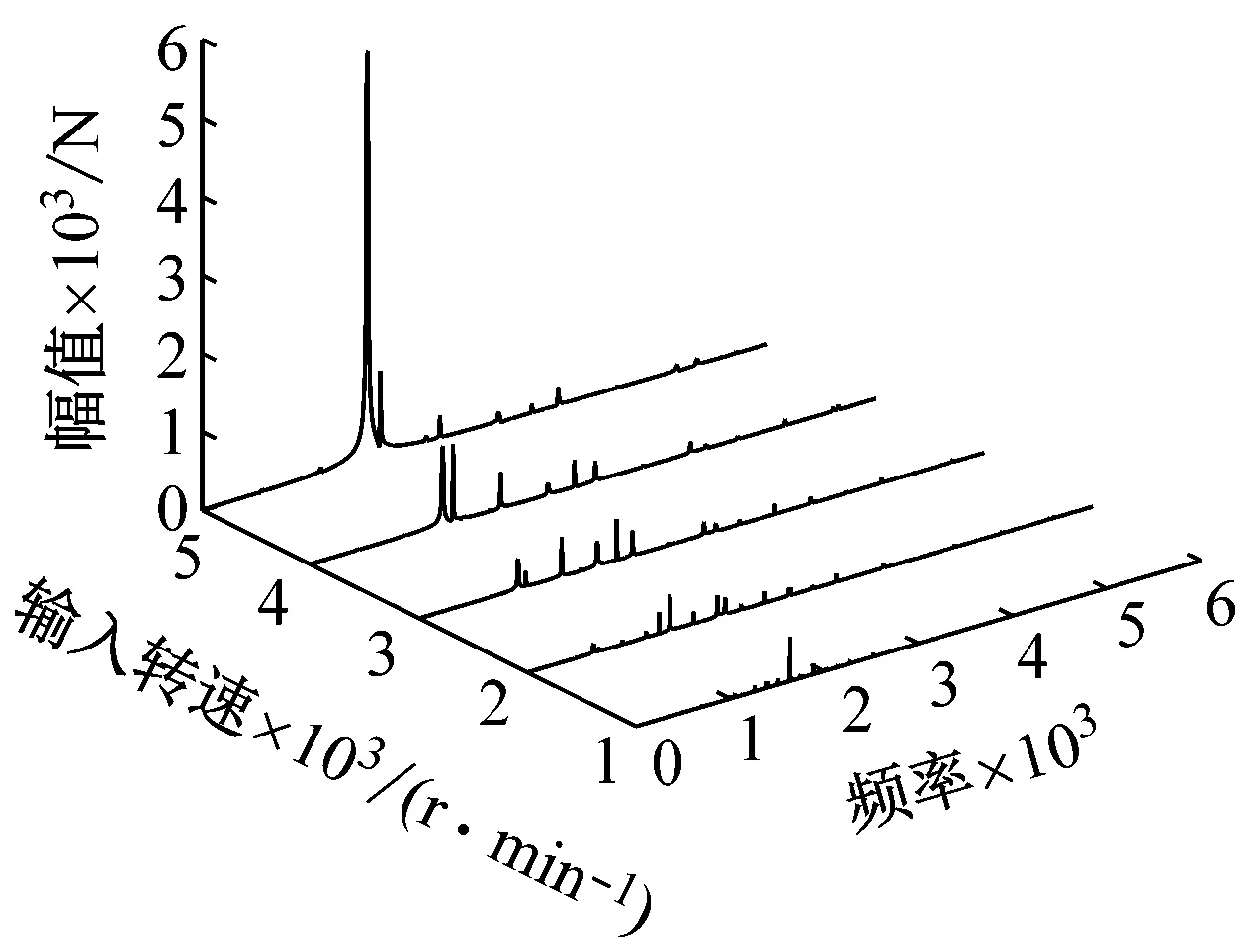
(e) 不同输入转速下动态啮合力Fm68频域响应图14 不同输入转速下各级动态啮合力频域响应Fig.14 Frequency domain response of various levels of meshing force at different input speeds
可以明显看出,各频率成分随着转速的不断增大,对应的幅值也不断提高。其中二倍输入级啮合频率2fm1的幅值相较于其他频率成分幅值增长幅度最大。
4.3 缺陷尺度变化对传动系统振动特性的影响
为了分析剥落缺陷的不同尺度对传动系统动态特性的影响规律,计算了当输入斜齿轮齿面双齿啮合区与三齿啮合区交界处存在长2 mm、4 mm以及8 mm剥落缺陷时系统的动态响应情况。如图15和16所示,为输入级斜齿轮无缺陷以及存在不同尺寸缺陷时的角加速度时域与频域图。
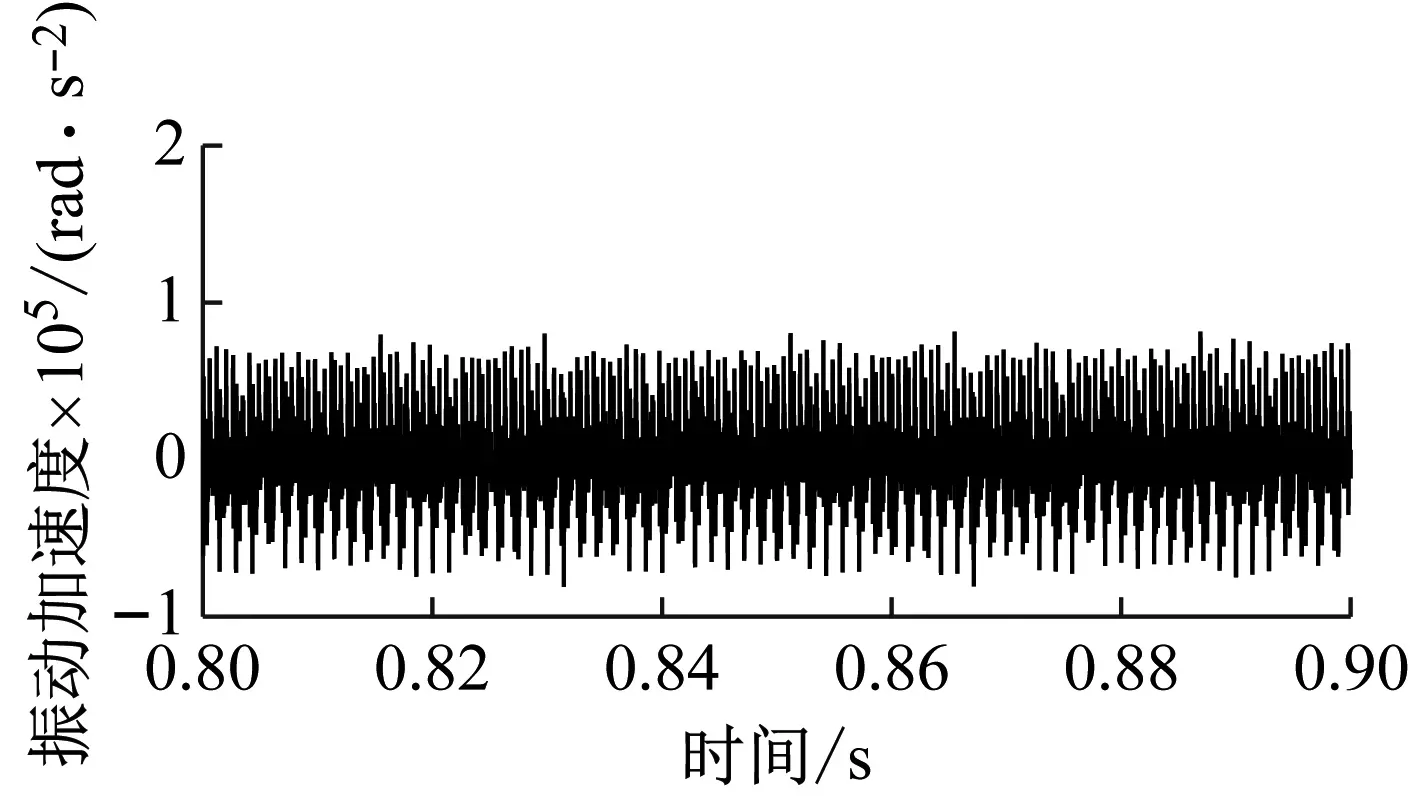
(a) 无缺陷输入齿轮角加速度时域响应
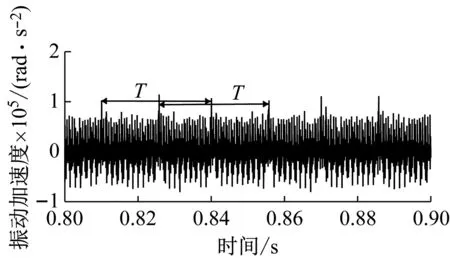
(b) 2 mm缺陷输入齿轮角加速度时域响应

(c) 4 mm缺陷输入齿轮角加速度时域响应
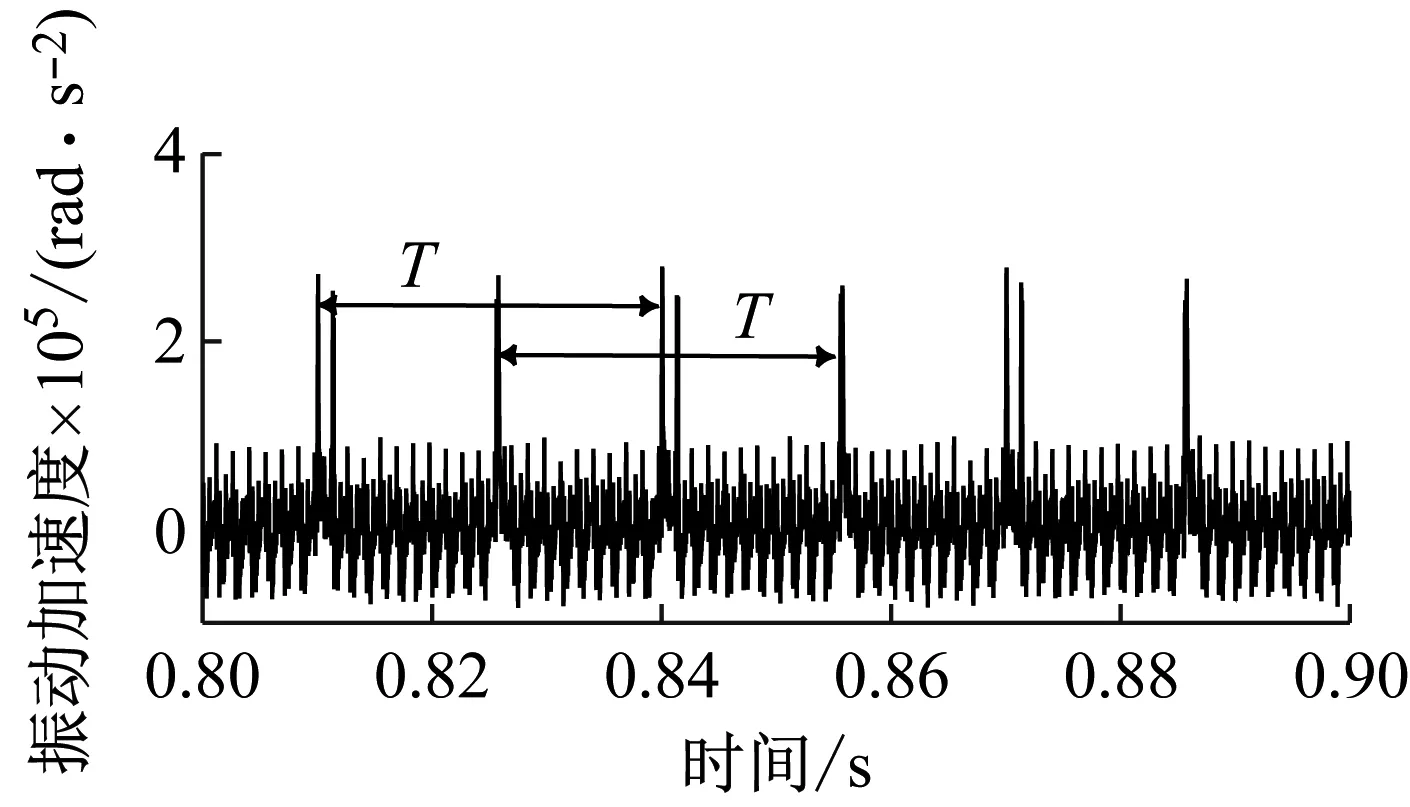
(d) 8 mm缺陷输入齿轮角加速度时域响应图15 不同尺寸缺陷输入齿轮角加速度时域响应Fig.15 Time domain response of input gear angular acceleration with different size defects
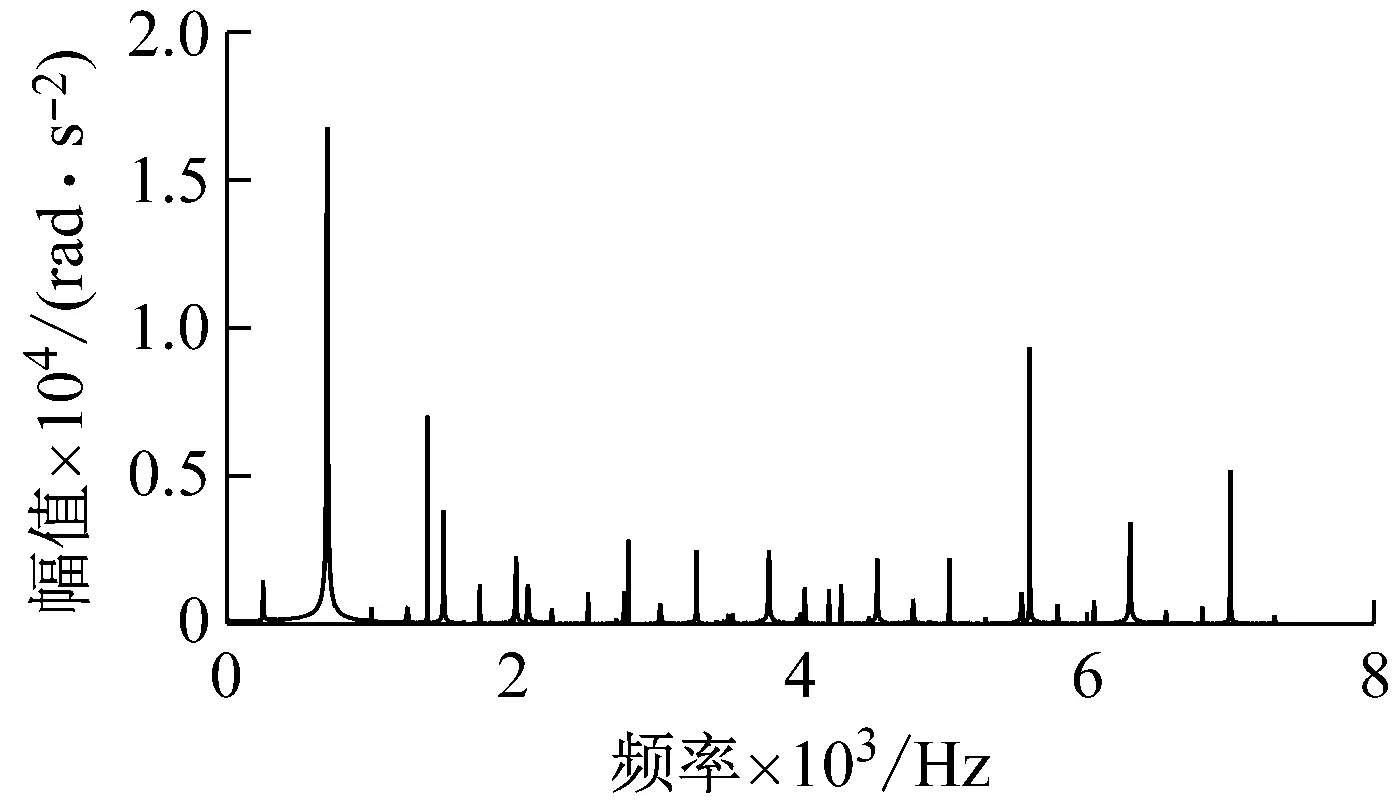
(a) 无缺陷输入齿轮角加速度频域响应
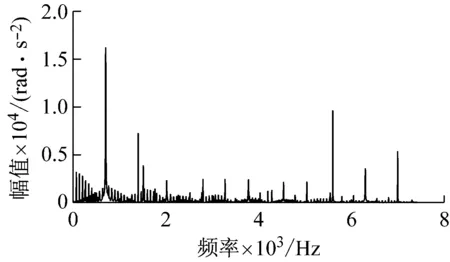
(b) 2 mm缺陷输入齿轮角加速度频域响应
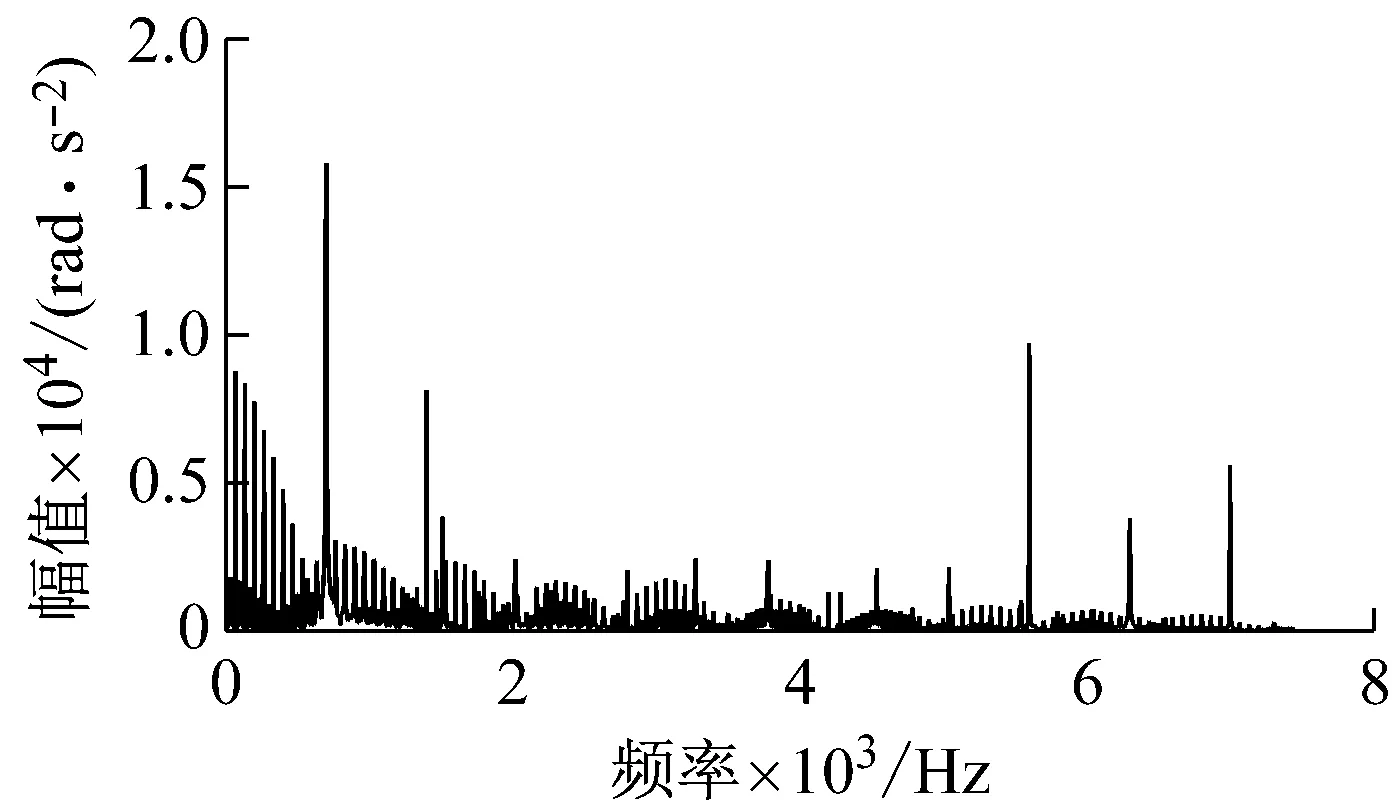
(c) 4 mm缺陷输入齿轮角加速度频域响应
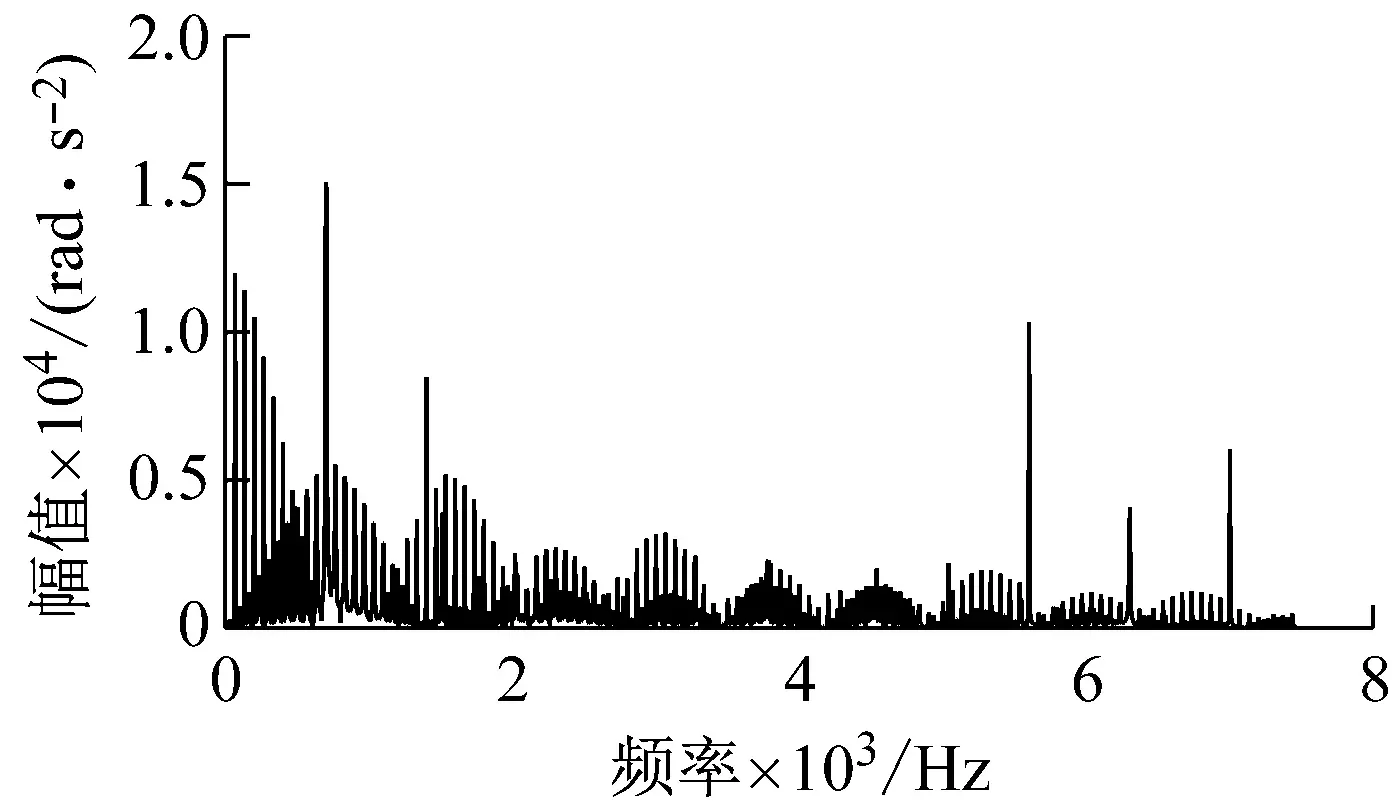
(d) 8 mm缺陷输入齿轮角加速度频域响应图16 不同尺寸缺陷输入齿轮角加速度频域响应Fig.16 Frequency domain response of input gear angular acceleration with different size defects
由于输入斜齿轮同时与其他两个斜齿轮啮合,因此当输入齿轮齿面存在缺陷时,时域图中每隔半个啮合周期出现一次振动冲击。从时域图对比可以发现,随着缺陷尺寸的增大,振动冲击的幅值也明显增大。计算齿轮Z1齿面缺陷长度为0、2 mm、4 mm和8 mm时,齿轮Z1旋转加速度时域响应的RMSE,如表2所示,RMSE依次增大,进一步反映出缺陷长度的增加明显加剧振动冲击的幅度。

表2 不同缺陷长度下旋转加速度时域响应的RMSETab.2 The RMSE of the time-domain response of rotational acceleration under different defect lengths
从频域图看,输入齿轮齿面剥落缺陷的产生使得振动加速度的频率成分在啮合频率附近出现明显的边频带,边频带成分主要由fm±nfc1构成,fc1为输入齿轮的转频。低频部分中的输入齿轮转频及其倍频和边频带的幅值随着缺陷尺寸的增加,也明显增大。
4.4 缺陷位置变化对传动系统振动特性的影响
传动系统由斜齿轮副组成,通过对斜齿轮副啮合刚度建模可以看出,时变啮合刚度由二齿啮合区和三齿啮合区交替并成一定周期组成。因此剥落缺陷存在的不同位置,势必对时变啮合刚度有较大影响,进而产生不同的动态特性。将剥落缺陷长度为4 mm,位置分别在双齿啮合区、三齿啮合区以及双齿与三齿啮合交界区时的时变啮合刚度的计算结果引入动力学模型中,得到图17和图18输入斜齿轮旋转加速度动态特性。通过与输入齿轮无缺陷时的振动加速度动态特性对比,可以发现缺陷存在不同位置产生不同的振动冲击效果。
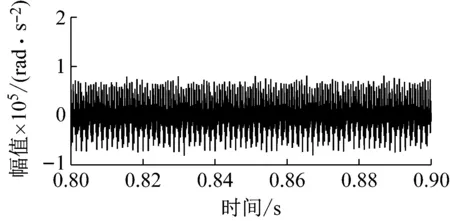
(a) 无缺陷输入齿轮角加速度
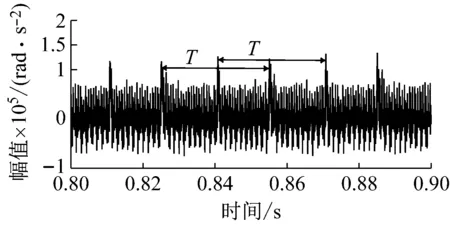
(b) 三齿啮合区缺陷输入齿轮角加速度
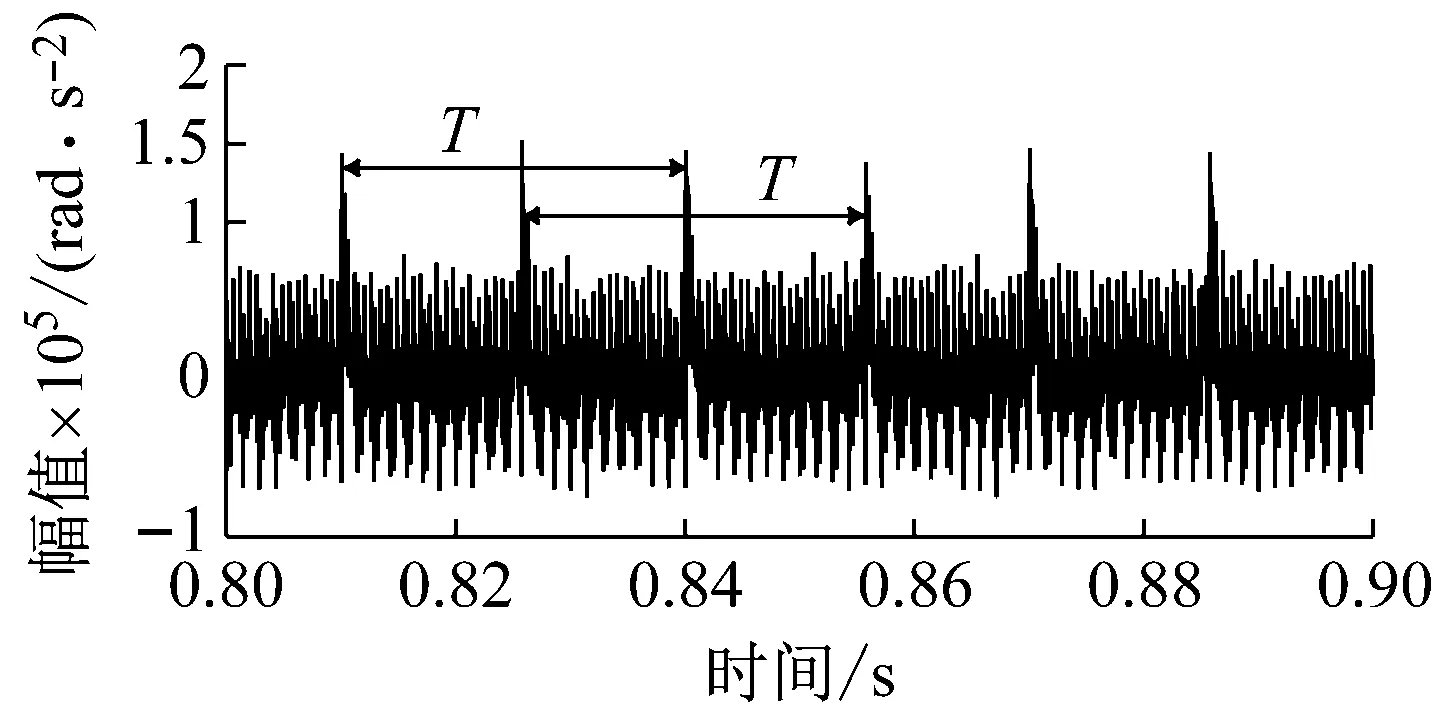
(c) 双齿啮合区缺陷输入齿轮角加速度
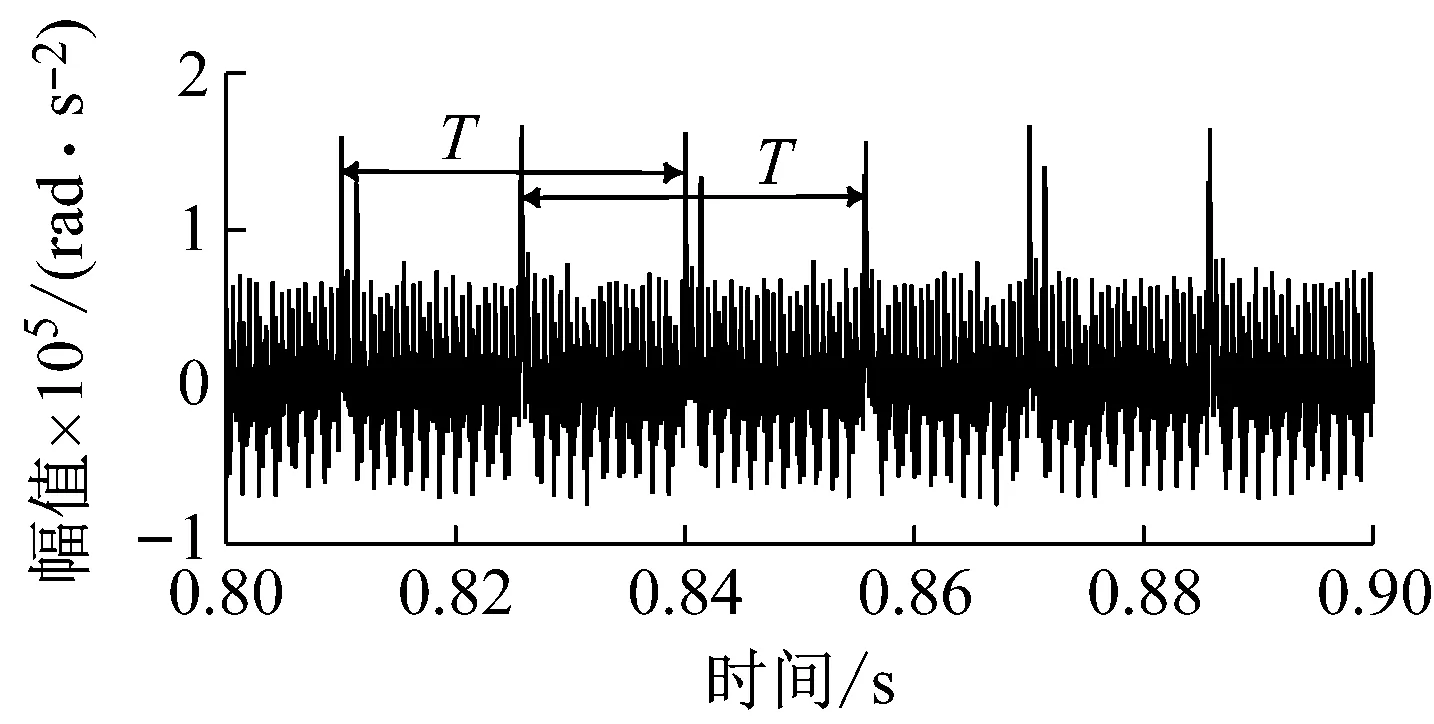
(d) 双齿啮合与三齿啮合交界区缺陷输入齿轮角加速度图17 不同位置缺陷输入齿轮角加速度时域响应Fig.17 Time domain response of input gear angular acceleration of different position defects
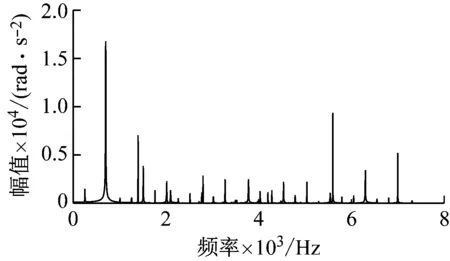
(a) 齿面无缺陷
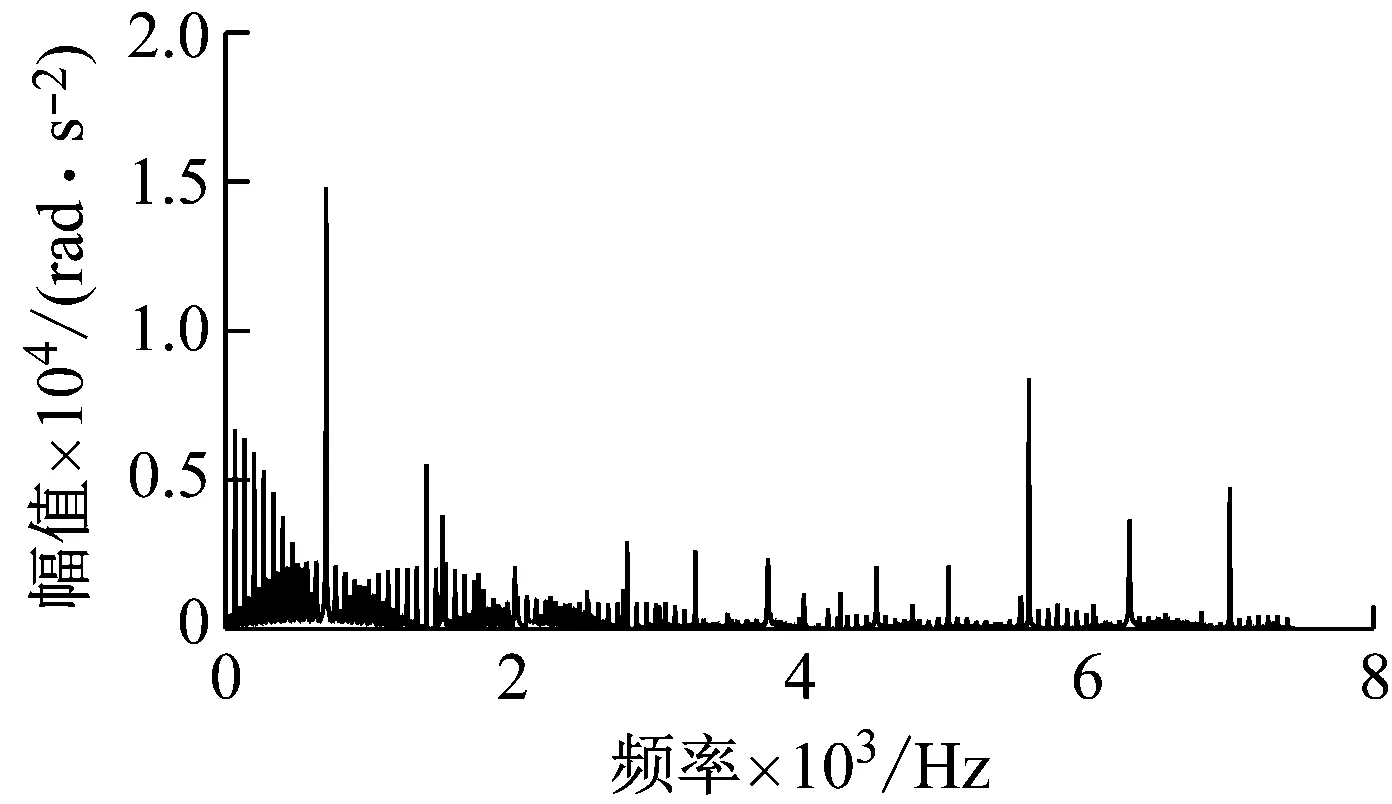
(b) 齿面三齿啮合区缺陷
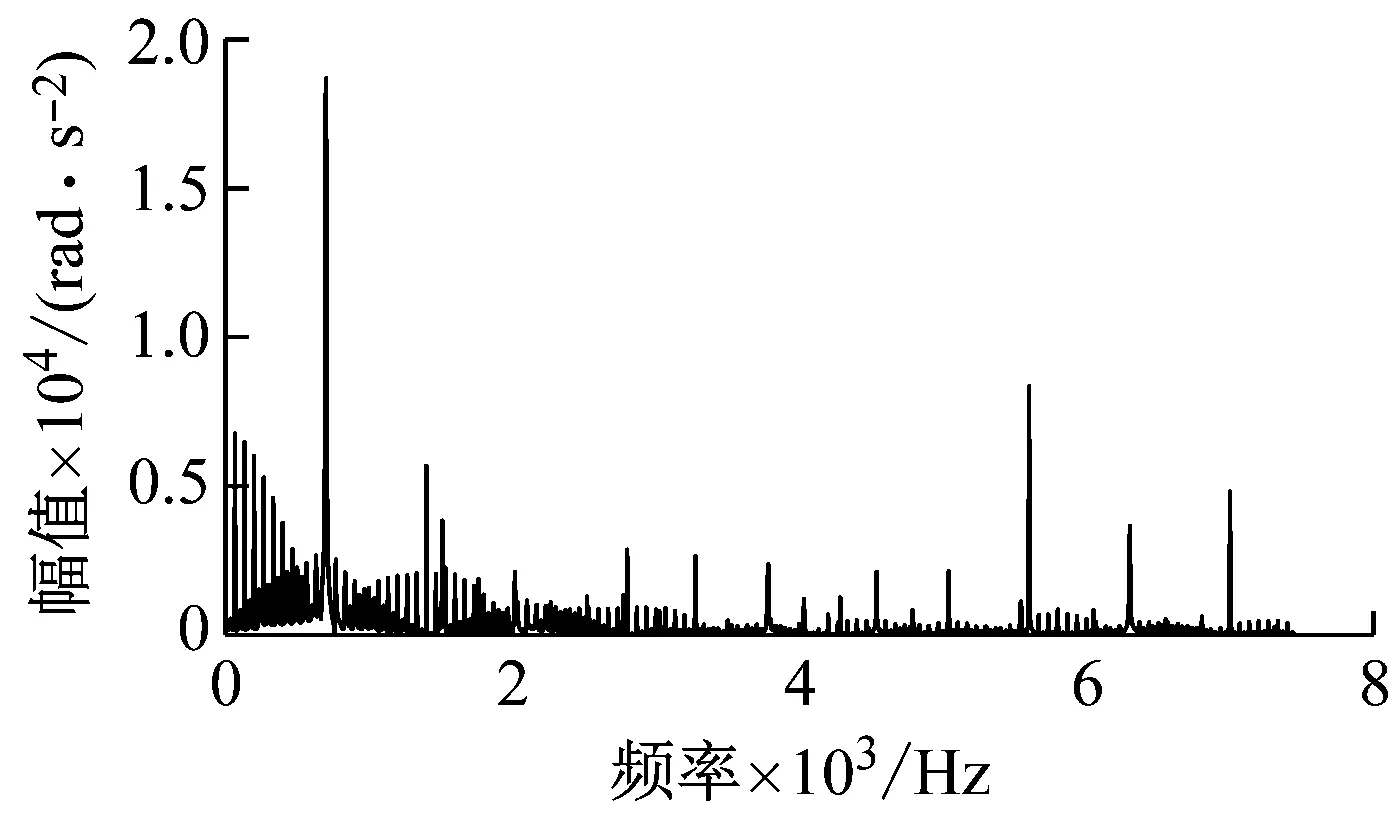
(c) 齿面双齿啮合区缺陷
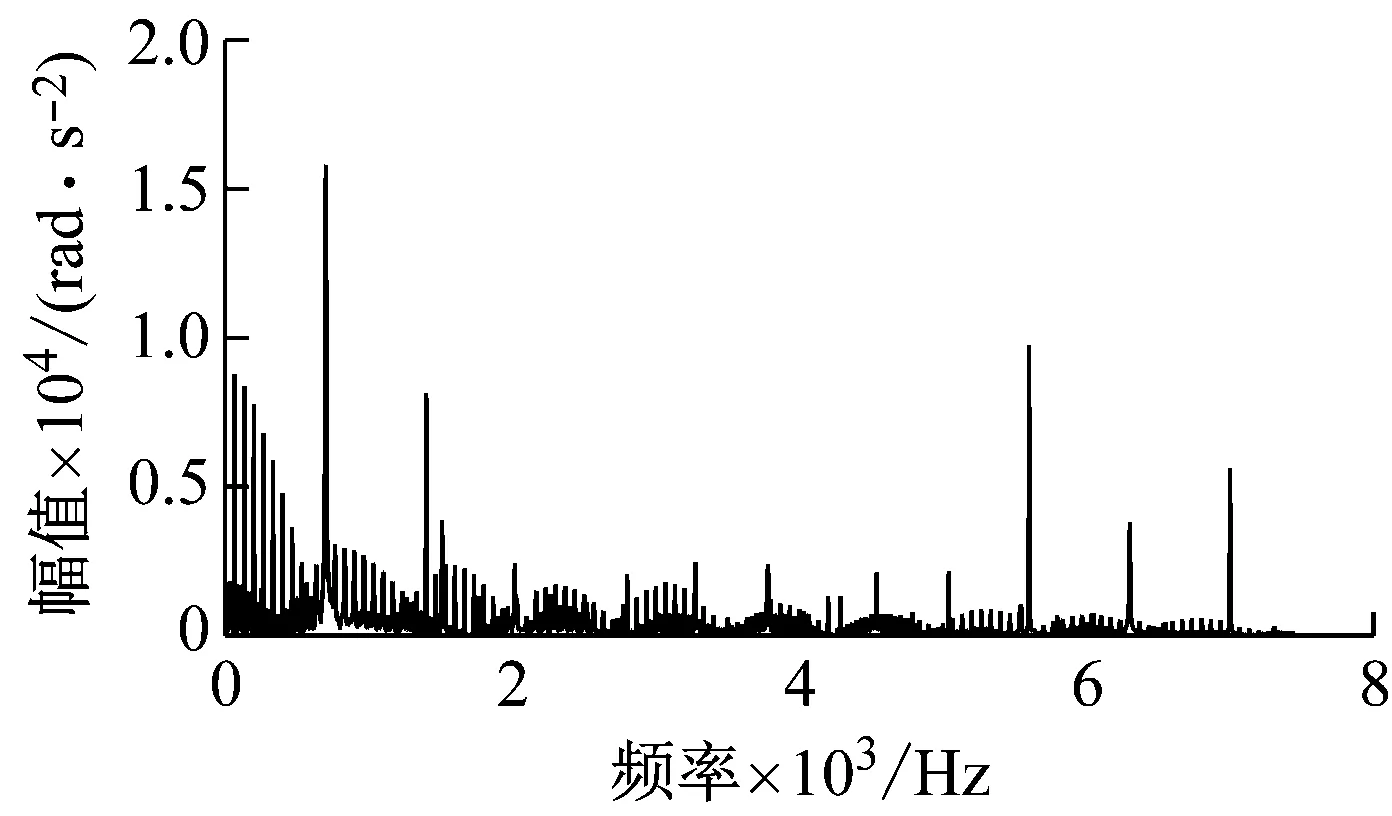
(d) 双齿啮合与三齿啮合交界区缺陷图18 不同位置缺陷下输入齿轮角加速度频域响应Fig.18 Frequency domain response of input gear angular acceleration of different position defects
观察时域图,缺陷存在双齿与三齿交界区时振动冲击的幅值最大,其次为双齿啮合区缺陷,三齿啮合区缺陷冲击的幅值最小。计算三齿啮合区缺陷,双齿啮合区缺陷和双齿与三齿啮合交界区缺陷冲击动态响应的RMSE,如表3所示。可以发现,虽然振动幅值最大为双齿与三齿啮合区交界处时振动冲击,但波动程度最大为双齿啮合区缺陷的动态响应。

表3 不同缺陷位置下旋转加速度时域响应的RMSETab.3 The RMSE of the time-domain response of rotational acceleration under different defect positions
频域响应中,双齿啮合区缺陷产生动态响应中低频部分边频带赋值与三齿啮合区缺陷的十分接近,但啮合频率fm1对应的幅值双齿啮合区缺陷明显大于三齿啮合区缺陷。双齿与三齿啮合区交界处存在缺陷时的频域响应中,边频带的幅值明显相较于双齿啮合区和三齿啮合区缺陷的更高。
5 结 论
针对某型无人直升机共轴对转主减多级斜齿轮传动系统,建立了其25自由度动力学模型。模型中考虑了轴承支承刚度、时变啮合刚度、传动轴扭转刚度以及啮合误差等因素影响。在此基础上,引入高速级齿面剥落缺陷模型,计算了不同尺度、位置缺陷下齿轮副时变啮合刚度的变化,进而分析缺陷尺度、位置变化对传动系统振动特性的影响规律。
(1) 基于上述动力学模型,分析了转速激励对各级齿轮副动态啮合力的影响。结果表明,驱动旋翼轴回转的齿轮副动态啮合力波动较大,驱动上旋翼轴回转的齿轮副动态啮合力波动程度是下旋翼齿轮副动态啮合力波动程度的1.7倍。
(2) 随着转速增大,各级齿轮副动态啮合力的幅值逐渐增大。频域分析表明,二倍输入级啮合频率对应的幅值增长幅度最大。
(3) 当输入齿轮齿面出现剥落缺陷,时域响应中产生较为明显的冲击。频域分析发现在啮合频率附近出现明显的边频带,边频带成分主要由fm1±nfc1构成。低频部分中的输入齿轮转频及其倍频和啮合频率附近边频带的幅值都随着缺陷尺寸的增加而明显增大。
(4) 通过分析缺陷位于双齿啮合区、三齿啮合区以及双齿与三齿啮合区交界处的三种位置变化对齿轮副动态响应的影响,发现当缺陷位于双齿与三齿啮合区交界位置时,振动冲击峰值最大。
