填土加筋对悬臂式挡墙地震响应影响的模型试验研究

魏 明， 罗 强， 蒋良潍， 王腾飞， 张 良， 连继峰

(1.西南交通大学 土木工程学院，成都 610031；2.西南交通大学 高速铁路线路工程教育部重点实验室，成都 610031； 3.西华大学 应急学院，成都 610039)

悬臂式挡土墙是由立壁和墙底板刚接而成的一种钢筋混凝土薄壁式支挡结构，具有自重轻、构造简单、对地基承载力要求低等优点，大量应用在路基工程的填方段。同时，也有对悬臂式挡墙墙后填土进行加筋，形成悬臂式挡墙加筋复合结构的工程实践[1]。然而，该类复合结构的研究目前主要为静力荷载下的受力和变形特性[2-3]，其在地震作用下的动力特性和地震响应有待进一步研究。

振动台模型试验具有直观、可重复性好等优势，是研究土工结构地震响应的一种重要手段[4-5]。关于悬臂式挡墙在地震作用下的振动台试验研究，大部分集中在单级或多级的悬臂式挡墙。如Kloukinas等[6]开展的振动台试验，讨论了不同几何尺寸及地基约束条件下悬臂式挡墙的动力响应特征及破坏模式。Atik等[7]基于超重力场振动台试验，分析了悬臂式挡墙的加速度及地震土压力等动力响应，得出地震惯性力和地震土压力的峰值并非同一时刻作用在墙体上，且地震土压力较拟静力设计值更小。Jo等[8]认为作用在墙体上的地震惯性力峰值和地震土压力峰值之间的相位差，与挡墙刚度、地震动频谱密切相关。高洪梅等[9]开展了墙后填土分别为聚苯乙烯泡沫(expanded polystyrene,EPS)混合土和南京细砂的悬臂式挡墙振动台试验，发现在两种填土条件下，墙背动土压力的分布形态存在较大差异，且EPS混合土-挡墙体系的加速度和位移相对更小，表明填土类型对墙-土体系的地震响应影响显著。何江等[10]综合三级拼装式悬臂式挡墙的振动台试验及数值模拟结果表明，填土加速度由墙底到墙高呈非线性放大，随着地震动幅值的增加，加速度放大系数呈增大趋势，墙-土体系逐渐由局部微小变形发展成过墙踵点整体滑动的破坏模式。可见，目前较少研究关注墙后填土加筋悬臂式挡墙的地震响应。

加筋土具有良好的抗震性能，广泛应用于高烈度地震区挡墙、边坡的加固[11-14]。Krishna等[15]对比研究了填土加筋和填土未加筋的刚性面板加筋土挡墙的动力响应发现，较未加筋而言，填土加筋可显著减小挡墙面板的位移，但对加速度和地震土压力影响较小。朱宏伟等[16]设计并制作了墙面板统一为预制砌块，而拉筋分别与墙背直接相连和包裹式回折的两种加筋土挡墙模型，基于振动台试验讨论了两种加筋土挡墙的动力响应差异，发现包裹式加筋土挡墙性能更优。徐鹏等[17-19]采用振动台模型试验，系统地研究了分块式面板和整体刚性面板加筋土挡墙的动力响应，并与相关设计规范进行了比较。Ding等[20]开展了混凝土帆布加固砾石边坡的一系列振动台模型试验，认为填土加筋可提高边坡在地震作用下的稳定性，且加载幅值大于临界加速度时，填土加筋减震效应才可有效发挥。王丽艳等[21]开展了废弃钢渣和传统砂土分别回填土工格栅加筋土挡墙的振动台试验，发现回填钢渣时加筋土挡墙的抗震性能更优，其原因是钢渣质量大且表面粗糙，颗粒与土工格栅摩擦作用显著。Panah等[22]开展了邻近岩石边坡加筋土挡墙的振动台试验，并与传统的加筋土挡墙对比，发现前者的抗震性能更优。此外，也有学者将加筋土技术应用于传统结构形式的挡墙。如杨长卫等[23]提出在重力式挡墙墙后填土中添加土工格栅，并与墙背直接连接的改进结构，随后开展的填土加筋与未加筋重力式挡墙振动台模型试验表明，填土加筋可抑制加速度放大和减小墙背土压力，适用于地震烈度8度以上区域。

综上所述，将加筋土技术移植到悬臂式挡墙中，以期发挥悬臂式挡墙刚性悬臂板的侧向变形约束作用，同时利用加筋土的良好抗震性能，但尚需对该类结构的地震响应开展更深入的研究。鉴此，基于大型1-g振动台设备，制作墙后填土未加筋与采用包裹式加筋的悬臂式挡墙模型，模型底部输入低幅值高斯白噪声和幅值为0.11g、0.24g、0.39g的简谐波。重点分析不同加速度幅值正弦波激励下，模型的自振频率及阻尼比，加速度沿高度放大，振动位移以及墙-土相互作用等规律，以对比模型动力特性及响应差异，明确悬臂式挡墙填土加筋的减震效应。研究成果可为墙后填土加筋的悬臂式挡墙抗震研究提供试验参考。

1 振动台模型试验概况

原型结构为高烈度地震区某高速铁路工程填方段的6 m高悬臂式挡墙，墙后填土采用拉筋长4.5 m，垂直间距0.3 m的包裹式加筋土加固。在此基础上进行模型概化，对原型结构缩尺设计，制作了填土加筋的悬臂式挡墙模型，同时，为对比填土加筋的减震效应，还制作了墙后填土未加筋的悬臂式挡墙模型。

1.1 试验设备及相似比设计

模型试验设备为计算机控制的电液伺服地震模拟振动台，沿水平方向单自由度振动，其主要技术指标如表1所示。

表1 振动台设备技术指标Tab.1 Technical specifications of the shaking table facility

配套模型土箱为自制的刚性箱，采用中空矩形截面型钢制作钢骨架，振动方向封闭端和两侧壁分别选用钢板和便于观察试验现象的透明有机玻璃制作。有机玻璃内侧粘贴透明塑料以减小边界摩擦，尽量保证模型结构处于平面应变条件。振动台及刚性模型箱照片如图1所示。

图1 振动台及刚性模型箱Fig.1 Photograph of the shaking table and rigid soil container

相似律设计是模型试验的关键问题之一。相似理论是将原型结构在静、动力荷载作用下的力学现象在模型结构上进行相似模拟，测量模型结构的响应物理量，再通过一定的相似法则推算到原型结构上。振动台模型试验相似律设计主要包括三部分内容，①模型制作遵循的相似关系，如几何比尺和填土密度；②模型加载相似准则，重点控制输入加速度的幅值和频率；③其余物理量的相似关系由上述控制量依据量纲分析原理导出。

需要说明的是，在重力场振动台缩尺试验中，模型应力小于原型结构，导致模型填土剪切模量亦小于原型。Hardin等[24]指出在小应变条件下，剪切模量G与应力σ的关系可表示为G∝σλ，λ为与土体种类有关的无量纲指数。Wood[25]认为对于砂土，λ取0.5较为合适，基于该模量修正指数的相似律逐渐应用于各种重力场振动台试验中[26-27]。综合考虑模型箱尺寸及振动台设备负载能力等因素后，确定几何比尺N=4、密度及加速度相似比为1，结合模量修正原理导出其余物理量的相似关系，如表2所示。

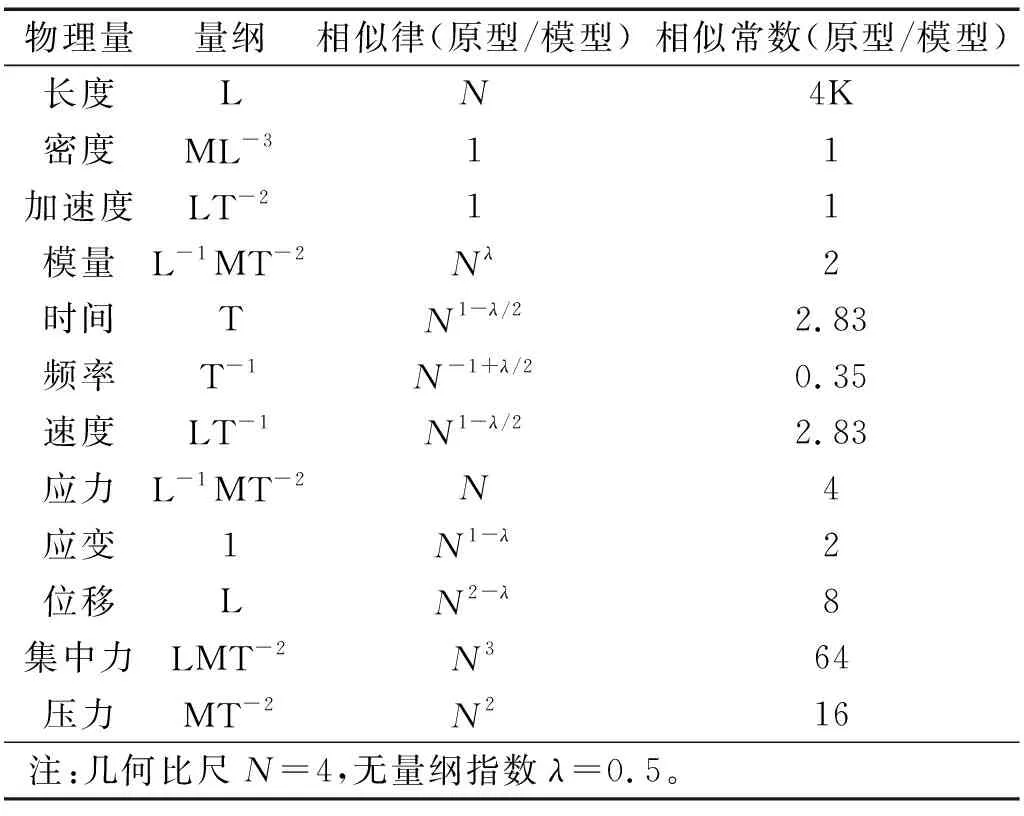
表2 模型试验相似律及相似比Tab.2 Scaling laws and ratios for the model test

1.2 模型制作及测试方案

1.2.1 模型制作

挡墙振动台模型的设计方案及测试仪器布置如图2所示。其中，图2(a)为墙后填土未加筋的悬臂式挡墙模型，图2(b)为墙后填土加筋的悬臂式挡墙模型。2组模型的几何尺寸相同，沿振动方向长3.26 m，垂直振动方向宽1.5 m，模型高1.5 m。挡墙底部与振动台面存在摩擦约束，地基条件均为刚性地基。悬臂式挡墙墙趾处设置限位块，使墙体仅绕墙趾转动而不产生水平滑动，类似的边界约束也见于其它研究[28]。填土加筋模型中，自下而上共铺设8层包裹式加筋网，筋带端部缠绕包裹体进行回折，悬臂板与包裹体的0.1 m间隙为92%压实度的粗砂垫层。此外，刚性模型箱内侧衬厚度40 mm的土工泡沫材料，以减小地震波反射，对试验造成干扰。

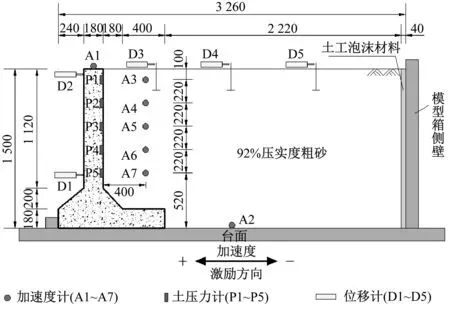
(a) 未加筋模型

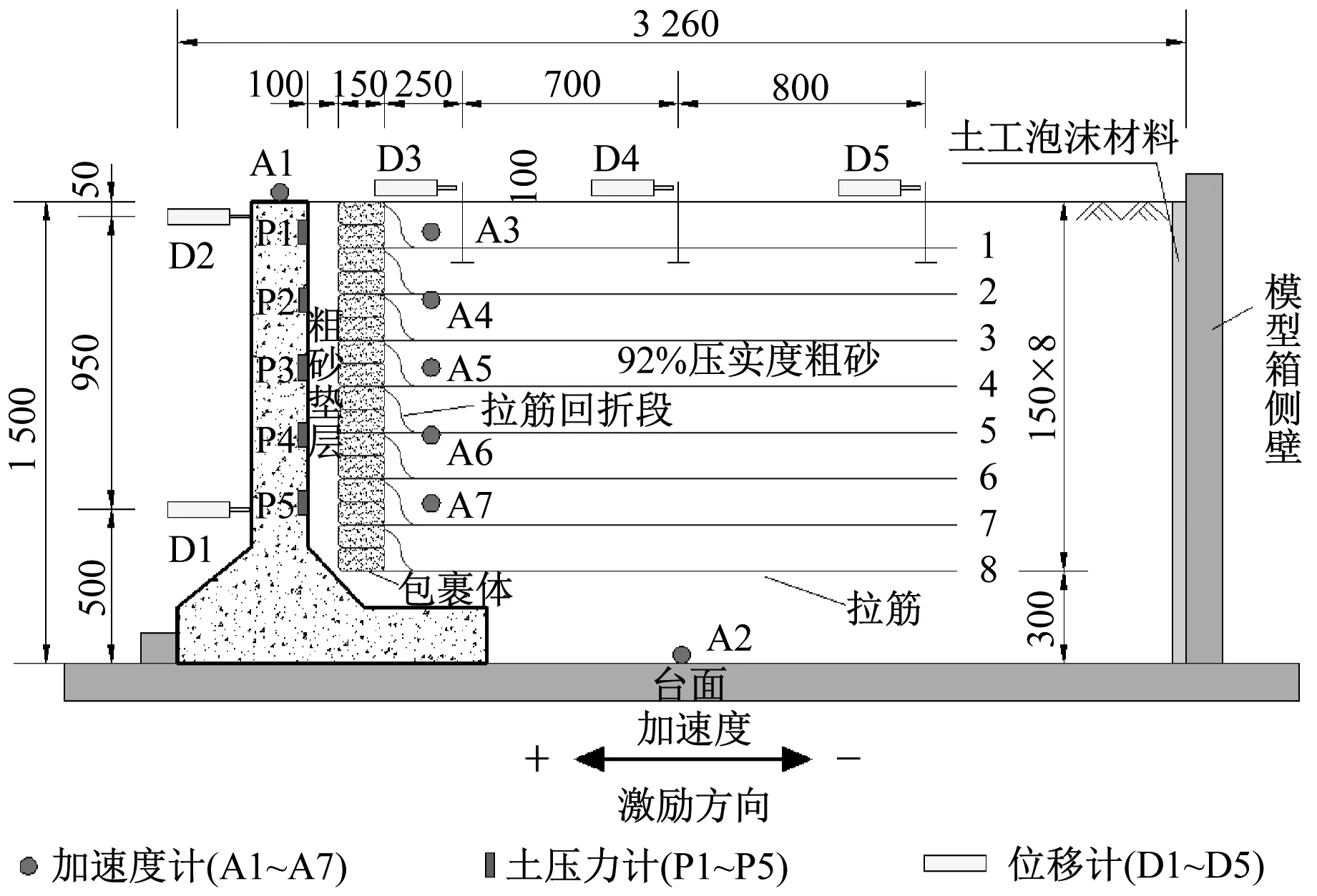
(b) 加筋模型图2 悬臂式挡墙模型设计方案及测试仪器布置(mm)Fig.2 Design schemes and instrumentations of the cantilever retaining wall models (mm)

试验材料包括填土、模型挡墙及拉筋，具体参数如下：

(1) 填土

填土选择风干的天然石英河沙，粒径分布曲线及特征粒径值如图3所示。填土属于均匀级配的粗砂，其物理力学特性参数如表3所示。

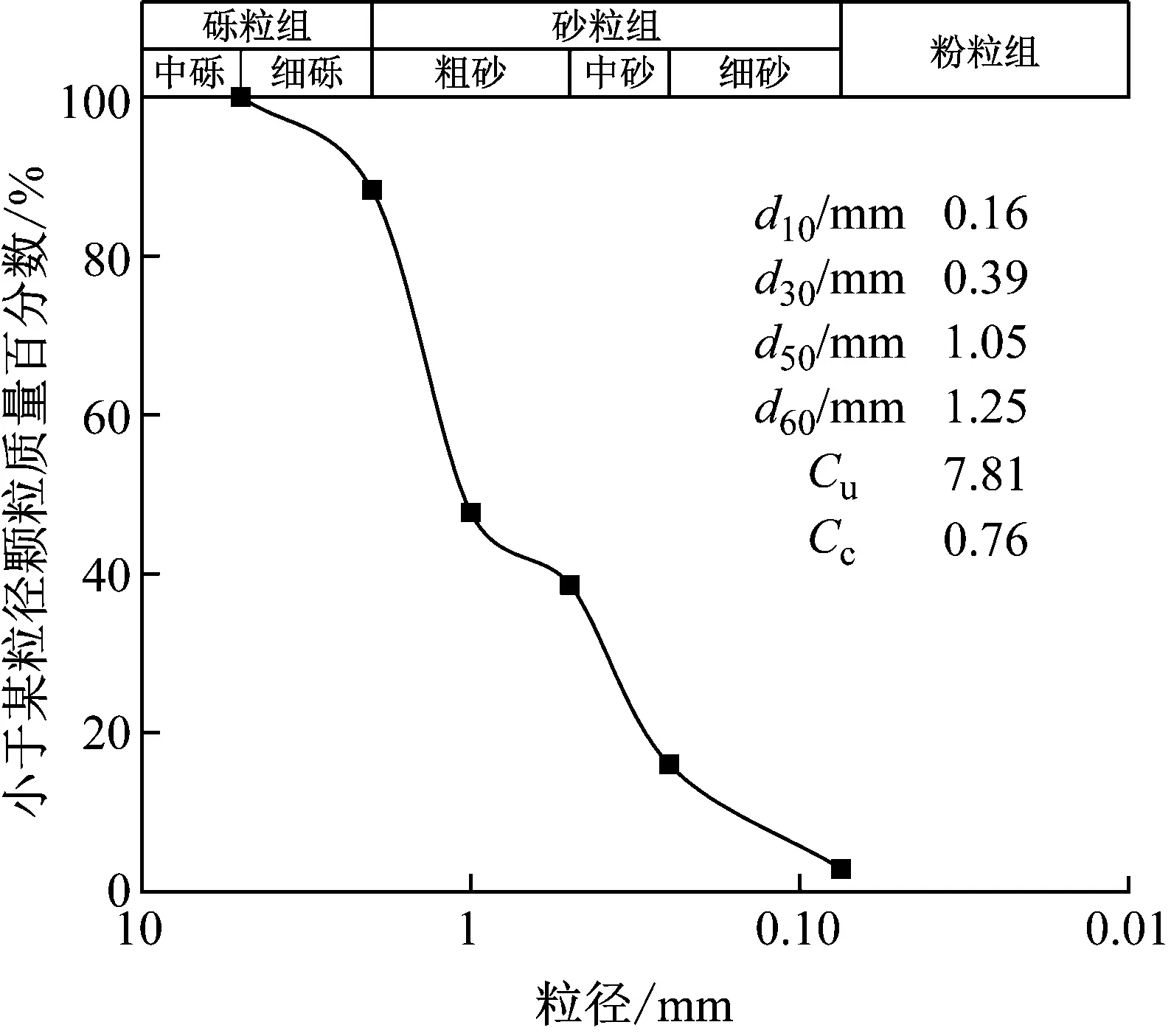
图3 填土粒径级配曲线Fig.3 Particle size distribution of the backfill soil

表3 填土物理力学参数Tab.3 Physical and mechanical properties of backfill

(2) 模型挡墙

原型工点挡墙高6 m，又缩尺比N=4，确定模型挡墙高H=1.5 m，其余尺寸及墙体构造如图4所示。模型挡墙混凝土强度为C40，配筋参照原型结构，浇筑模型时在立壁板墙背侧预留凹形圆孔，以安装土压力盒P1～P5。根据Veletsos等[29]定义的土-墙相对柔度比dw，选取砂土弹性模量经验取值范围约60～80 MPa，估算得dw≈4.72～6.29，挡墙体系属于一种较刚硬的结构。

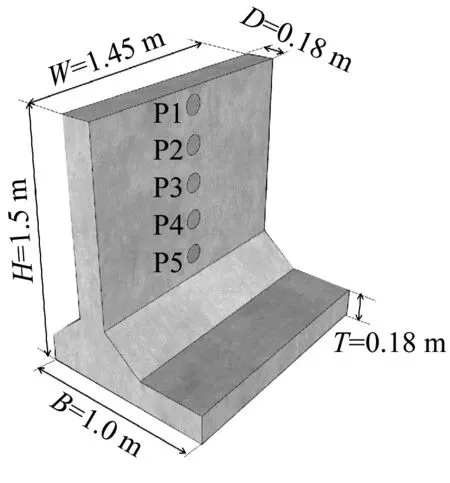
图4 模型挡墙Fig.4 Reduced-scale of retaining wall

(3) 拉筋材料

在加筋土的模型试验中，拉筋通常采用强度相似[30]或刚度相似[31]的原则进行模拟，以实现模型与原型筋材力学行为的相似。原型拉筋为高密度聚乙烯制作的单向拉伸塑料土工格栅，设计抗拉强度80 kN/m。参考已有学者[32-33]采用磷青铜带模拟土工格栅的经验。本研究选用厚度0.2 mm磷青铜带焊接成网，以强度相似原则模拟原型土工格栅，结合模型尺寸及制作简易性，确定网格尺寸为0.3 m(纵向)×0.15 m(横向)，如图5所示。模型单层筋带抗拉强度11.2 kN/m，竖向距离0.15 m。依据模型试验相似律换算，等效于原型以0.3 m垂直间距，抗拉强度89.6 kN/m布置的高强土工拉筋。

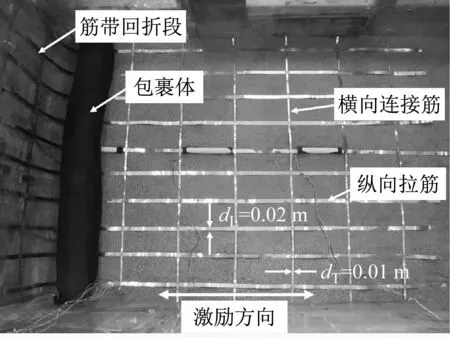
图5 筋带网照片Fig.5 Photograph of reinforcement layer

1.2.2 数据采集与传感器布设

(1) 测点布置及传感器参数

本文重点探讨填土加筋对悬臂式挡墙和填土动力响应的差异，因此，在挡墙上布设了加速度计、土压力计和位移计，在填土中布设了加速度计和位移计。填土加筋模型和填土未加筋模型的传感器测点布设位置和数量完全一致(见图2)。测试传感器汇总如表4所示。

表4 测试传感器汇总Tab.4 Technical specifications for the instrumentations

共使用7个MEMS加速度传感器，A2监测地震输入，A1、A3～A7分别测试挡墙和填土各高度处的振动时程。在墙背处共安装5支电阻应变式土压力计，动态测定墙背土压力响应。模型结构中共布置5支位移计，其中，D1为测量墙体下部振动位移的电涡流传感器；D2、D3～D5分别测量墙体上部及填土表面的振动位移，振动较小时采用量程为5 mm的电涡流传感器，振动较大时改用量程为100 mm的LVDT(liner valiable differential transformer)位移计，以提高测试精度。

(2) 传感器安装

①为保证加速度计的拾振方向与台面激励方向一致，首先将A3～A7加速度计分别固定在小块的底座上，并采用铝盒罩保护，避免损坏，最后按图2中的传感器布置图埋设于填土中。A1和A2加速度计分别固定于挡墙顶部及振动台面；

②土压力计等间隔固定于墙背预留凹形圆孔中，承压面与墙背面齐平，土压力计与圆孔接缝处使用704硅胶固定，起到防水的作用。

③所有位移传感器均采用与振动台螺栓连接的刚性夹具固定，故所测位移为模型结构测点相对振动台的动态位移。位移计安装完成照片如图6所示。

(a) 整体照

(b) 局部放大照图6 位移传感器安装Fig.6 Photograph of displacement transducers installation

1.2.3 模型填筑

模型采用“体积质量法”分层压实填筑，分层高度为0.15 m，共分10层填筑，控制填土压实系数约0.92，即密度约1.76 g/cm3。以填土加筋模型为例，模型填筑过程具体步骤如下：

①安装悬臂式挡墙。将预制好的模型挡墙吊装至模型箱中，墙背预设凹槽处安装土压力计，挡墙与模型箱侧壁的缝隙填充土工泡沫，防止漏砂。

②人工压实填土。人工压实模型底部2层砂土至0.3 m高，为加筋体填筑提供水平的基准面。

③加筋体及粗砂垫层填筑。首先，将筋带网平整铺设在填土上，包裹体整齐码放于筋带预设回折处；其次，将筋带回折紧紧缠绕包裹体，包裹体后侧填土压实至分层填筑线；最后，悬臂板与包裹体之间预留的0.1 m宽间隙填筑相同密实度砂土。严格执行“逐层填筑加筋体，逐层填筑粗砂垫层”的工艺，重复步骤③共8次，完成模型填筑。

④布置传感器。在填筑过程中，预定位置处埋置加速度计，在填筑完成后，安装位移计。

1.3 加载制度

振动台试验加载波形通常有简谐波和随机地震波，尽管地震波更接近真实振动，但简谐波因其波形简单、便于数据分析，被广泛用于振动台试验[34]。为测试模型的动力响应，台面逐级输入加速度幅值分别为0.11g、0.24g及0.39g的正弦波，在本文中依次简称为小震、中震及大震，频率固定为5 Hz，依据表2中的频率相似常数，对应原型结构所受地震波的主频约为1.75 Hz，处在常见天然地震波的主频范围内。在试验模型进行振动加载前和各级简弦波振动后，输入加速度幅值约0.05g、振动持时约30 s的高斯白噪声扫频，识别墙-土体系的自振频率和阻尼比。

2 试验结果与分析

2.1 墙-土体系动力特性

挡墙-填土体系动力特性包括自振频率和阻尼比。振动台面输入低幅值高斯白噪声扫频后，得到台面A2和模型中A1、A3～A7测点的加速度时程数据，参照蒋良潍等[35]的方法计算台面输入和结构输出响应之间的频响传递函数。频响传递函数是以频率为自变量的复函数，绘制其虚部-频率特性曲线，采用峰值法和半功率带宽法分别确定自振频率fn及阻尼比ζ，以未加筋模型墙顶A1测点为例加以说明，如图7所示。其余测点的自振频率和阻尼比类似确定。

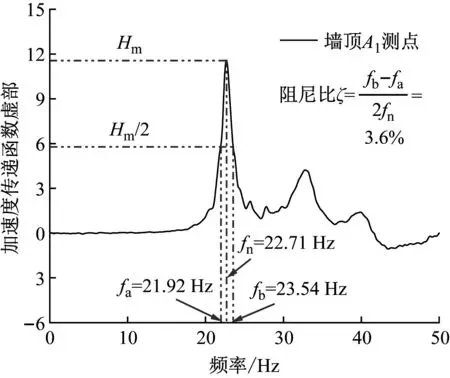
图7 加速度传递函数虚部-频率特性曲线Fig.7 Transfer function imaginary part-frequency characteristic curve of acceleration

测试数据表明，不同测点的自振频率和阻尼比差异不大，故取6个测点的平均值代表模型整体的自振频率和阻尼比。两组模型墙-土体系动力特性随加载进程的变化如图8所示。在施加振动前，未加筋模型和加筋模型的自振频率基本一致，分别为22.71 Hz和22.69 Hz。随着振动强度的增大，模型的自振频率和阻尼比分别呈减小和增大的基本规律，适用于加筋模型和未加筋模型。产生该现象的原因是，随着振动强度的增大，结构损伤逐渐累积，土体非线性特征显现。

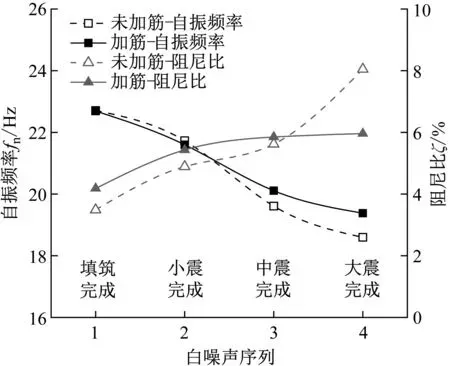
图8 墙-土体系动力特性随加载序列的变化Fig.8 Variation of dynamic characteristics of wall-soil system with loading sequence

为定量评估不同强度地震动作用下，模型自振频率的减小程度和阻尼比的增大程度，定义自振频率减小率为各量级地震动作用后，模型自振频率相对未施加振动前的减小百分比，阻尼比增大率为各量级地震动作用后，模型阻尼比相对未施加振动前的增大百分比。加筋模型和未加筋模型的自振频率减小率、阻尼比增大率，如表5所示。

表5 墙-土体系动力特性的变化率Tab.5 The variation ratio of dynamic characteristics of the wall-soil system

模型自振频率减小反映了结构整体刚度退化，阻尼比增大反映出结构损伤增加，结构耗能提高[36]。由表5可知，在小震0.11g作用下，未加筋模型和加筋模型的自振频率减小率差异不大，而阻尼比增大率分别为40.1%、29.9%，表明在小震激励后，两组模型均出现微弱损伤，但加筋模型的损伤程度更小。中震0.24g激励下，未加筋模型和加筋模型的自振频率分别减小13.7%、11.4%，相应地，阻尼比分别增加61%、40%，模型损伤进一步加剧，但加筋模型的整体刚度退化程度和伤损程度较未加筋模型更小。大震0.39g激励后，两组模型的自振频率均大幅减小、阻尼比均大幅增大，表明模型在较大震动强度作用下产生严重损伤，然而加筋模型的自振频率和阻尼比变化幅度均小于未加筋模型，尤其是对伤损程度较敏感的阻尼比，后者仅为前者的32.6%。综上可知，填土加筋模型的自振频率减幅和阻尼比增幅均较未加筋模型更小，表明墙后填土加筋相对未加筋可减小整体刚度的退化程度、减弱结构损伤，更能保持墙-土体系的整体性，进而改善挡墙-填土体系的动力特性。

2.2 加速度响应

为描述地震加速度在结构模型中各处的放大效应，定义加速度放大系数Am为各测点的均方根加速度与振动台面输入地震动均方根加速度的比值，该法可综合考虑地震动幅值和频谱的影响，降低高频信号干扰[37]。各测点的Am如式(1)计算。

(1)

式中：aj(t)为测点j的加速度时程;b(t)为振动台面加速度时程;Td为振动持时;dt为时间间隔。

不同振动强度激励下，两组模型的加速度放大系数Am沿墙高的对比,如图9所示。首先，填土加筋与未加筋表现出一些相似规律：①随着测点位置的增高，Am逐渐单调增大，且增大趋势愈加显著，悬臂式挡墙墙顶处的放大系数略大于填土表面；②随着振动强度的逐级提高，相同测点的加速度放大系数呈单调增加的规律，以未加筋模型的填土表面A3测点为例，小震、中震及大震激励下，加速度放大系数Am分别为1.3、1.64及2.43。

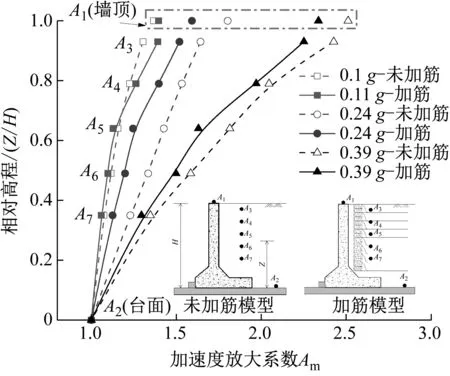
图9 加速度放大系数Am对比Fig.9 Comparison of acceleration amplification factor Am

其次，加筋模型的加速度放大系数Am整体上小于未加筋模型，表明墙后填土加筋可有效降低地震动的放大效应，阻隔地震力的传递。具体而言，0.11g作用下，填土加筋后，墙顶及填土上部的加速度放大系数Am较未加筋更小，而在填土下部Am差异不大。0.24g激励下，填土加筋后，墙顶及填土各处的放大系数均有所减小，相同位置处加速度放大系数减小率处于7.5%～11.7%范围内，填土加筋可抑制加速度放大。0.39g激励下，加速度放大系数相应减小约3.7%～10.2%。出现这一现象的可能原因是，剪切波由底部传播至土体时，地震能量转换成土的变形做功、振动能以及土颗粒之间摩擦以内能的形式耗散等三大部分，加速度放大系数是振动能量的间接体现。填土加筋后，地震能量还转换成筋带的弹性功和塑性功，使得振动能量相应减小，从而导致加速度放大效应减弱。此外，填土加筋后，土体的动力特性也发生了改变。

2.3 位移响应

2.3.1 挡墙振动位移状态定义

填土加筋模型在0.24g的基底加速度激励下，振动台台面A2、墙顶A1、填土表面附近A3加速度计及近墙顶土压力P1、近墙顶位移D2的典型响应时程曲线,如图10所示。

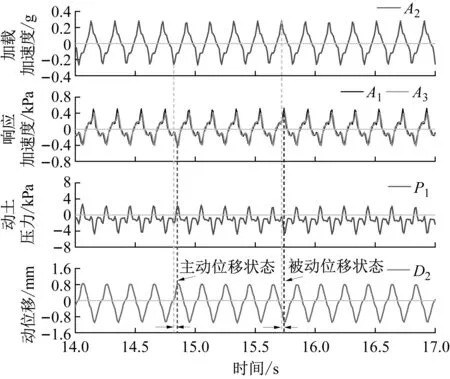
图10 测试量时程曲线Fig.10 Time history of dynamic displacement, earth pressure, response acceleration, and input acceleration

首先，结构模型上部各测试量较台面加速度A2存在一定的时间延迟Δt，表明振动波由底部传播至上部时具有滞后性，故台面输入与模型结构响应不同步。其次，考虑到墙体刚度较大，并且近墙顶处的动位移D2和加速度A1同步运动，因此可依据动位移D2，将墙体运动状态划分成两种极限状态：主动位移状态和被动位移状态。其中，主动位移状态时，墙-土相互作用表现为“土推墙”，墙体位移和墙体惯性力同时达到朝临空侧的最大值，此时挡墙处于最不利状态；被动位移状态时，墙-土相互作用表现为“墙推土”，墙体位移和墙体惯性力同时达到朝填土侧的最大值。对于挡墙稳定性而言，更应关注墙体处于最不利位移状态时各测试量的响应。

2.3.2 墙体位移

如模型制作中所述，墙趾处进行约束，震后永久位移较小，本文仅讨论墙-土相互作用最不利时的结构峰值振动位移。最不利状态时，2组模型的墙体水平位移及转角随加载幅值的变化曲线,如图11所示。从图11可知，悬臂板的峰值振动位移随加载幅值的增加呈非线性增大，小震作用下，2组模型的振动位移区别不明显，中、大震激励下，加筋模型的水平振动位移较未加筋模型明显减小。

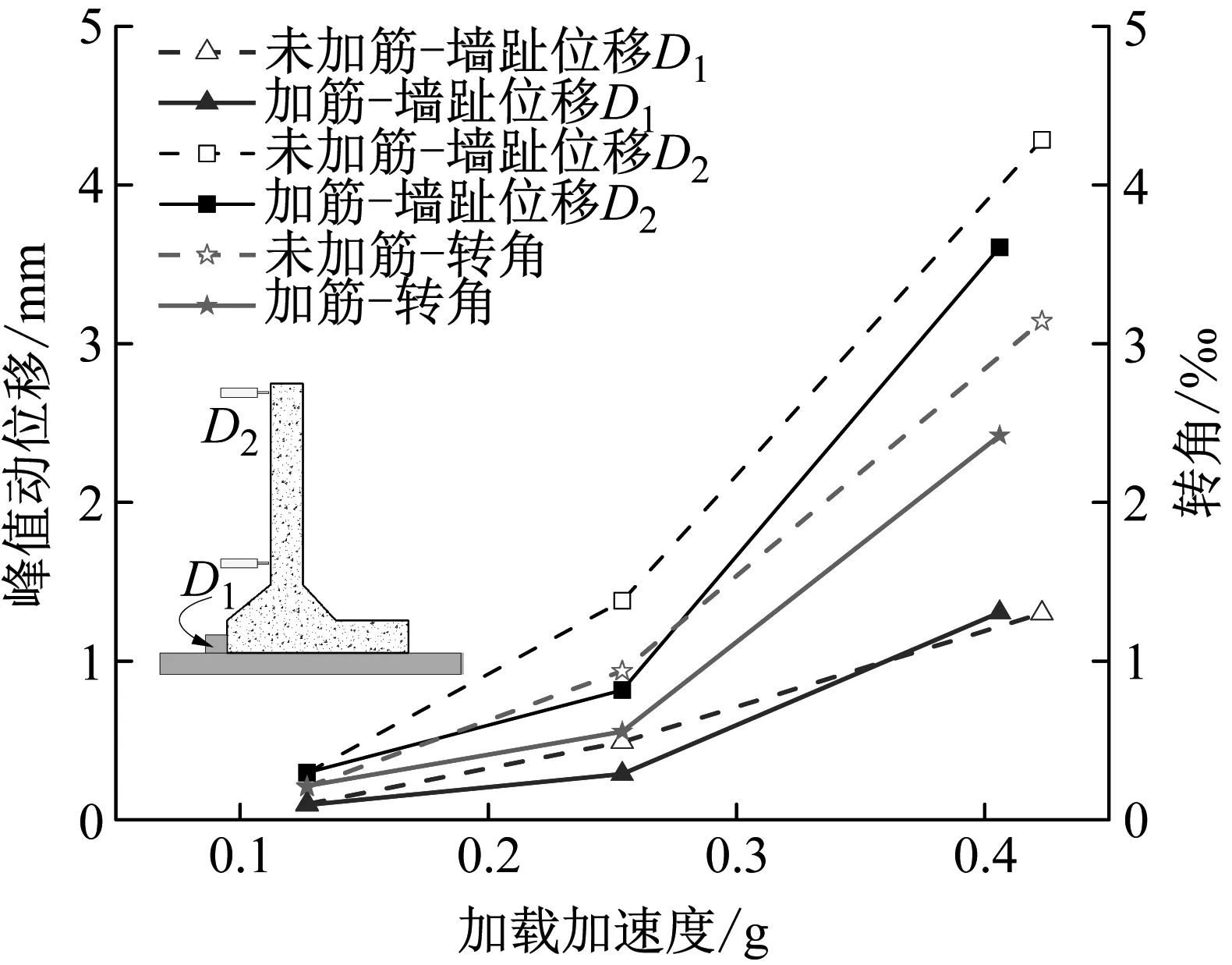
图11 最不利状态下墙体位移及转角随加载幅值变化Fig.11 Angle of rotation and displacement of the facing panel vs. input acceleration at the most unfavorable condition

0.11g激励下，填土加筋与未加筋模型的转角近似相等，加筋效果不明显。0.24g作用下，加筋与未加筋模型的墙顶水平振动位移分别为0.817 mm、1.38 mm，减幅近40.8%，悬臂板转动角相应减小约33.3%，表明填土加筋可抑制墙面板的振动位移。0.39g时，加筋前后墙顶位移分别为4.285 mm、3.607 mm，墙顶位移和墙体转角分别减小15.8%、22.6%。填土加筋后墙体振动位移明显减小，这是由于填土对挡墙的侧向挤压作用有所降低。

2.3.3 填土表面位移

在最不利的主动位移状态时，墙顶位移D2和填土表面位移D3～D5随加载幅值的变化曲线,如图12所示。

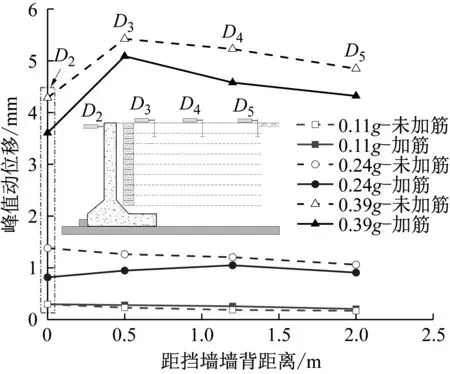
图12 最不利状态下填土及墙顶位移随加载幅值变化曲线Fig.12 Dynamic displacement of backfill and top of facing panel vs. input acceleration at the most unfavorable condition

由图12可知，无论填土加筋与否，随着加载幅值的增大，填土位移幅值呈非线性增大的趋势。填土位移的空间分布规律在不同加载幅值作用下存在一定差异。在小震和中震作用下，模型填土不同测点的位移大致相当，在空间上呈均匀分布的规律，而在大震作用下，距临空侧最近的D3测点填土位移最大，距临空侧最远的D5测点填土位移最小，即距临空侧的距离越远，填土位移近似呈单调减小的空间分布趋势。

0.11g加载下，2组模型的填土平均位移差异不大，说明小震作用下加筋措施对填土位移约束不明显，其可能原因是加载幅值尚未达到减震效应发挥的临界阈值，与Ding等的试验现象类似。0.24g激励下，未加筋模型中填土平均位移为1.177 mm，加筋模型中的填土平均位移0.969 mm，后者较前者减小17.7%。0.39g激励下，相应的填土平均位移分别为5.166 mm、4.663 mm，减小9.7%。表明相同加载幅值下，加筋模型的填土位移小于未加筋模型，表明填土的加筋效应可约束填土位移，尤其是在中震及大震加载下较为明显。

需要特别指出的是，由图12还可知，小震及中震下，2组模型的墙顶位移与填土位移均大致相当，说明墙-土相互挤压的趋势不显著。大震作用下，无论填土加筋与否，墙后土体的水平位移均明显大于悬臂板的水平位移，意味着在振动过程的最不利位移状态时，刚性的悬臂板约束了填土位移，填土追挤悬臂板，筋-土的差异变形较小，使得大震时填土加筋的减震效应发挥有待进一步提高。

2.4 土压力响应

2.4.1 土压力与墙体惯性力同步性

每级振动施加前，墙背处的P1～P5土压力计归零，测得振动过程中填土作用在墙背处的土压力增量，本文称为动土压力。振动过程中墙体受到惯性力和土压力的双重作用，惯性力采用墙顶加速度A1乘以每延米挡墙质量的负值计算；基于墙背P1～P5土压力测点数据，并假设测点之间土压力强度呈线性分布，采用包络线法计算动土压力的合力。

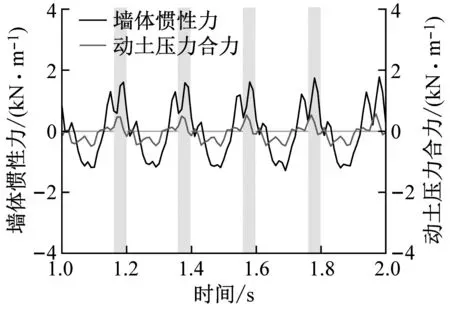
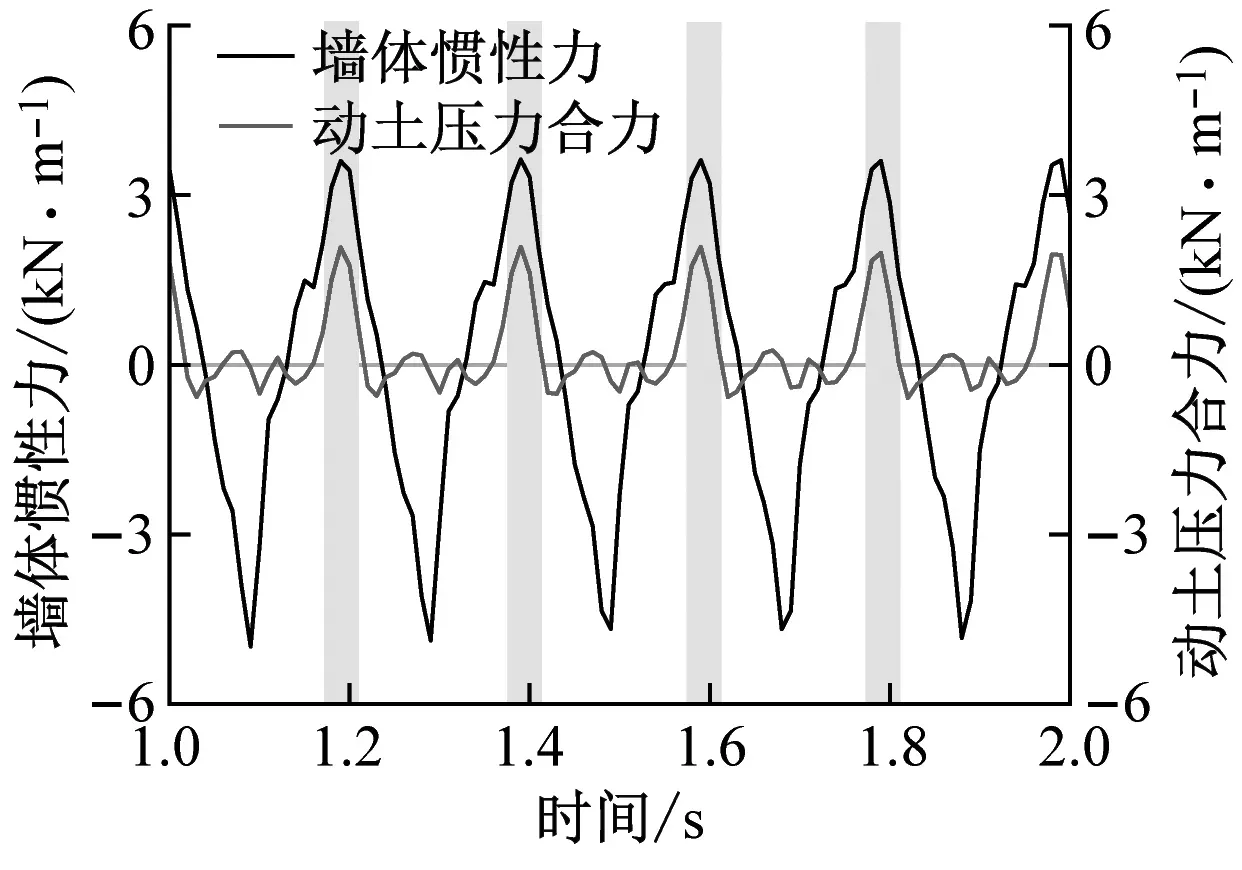
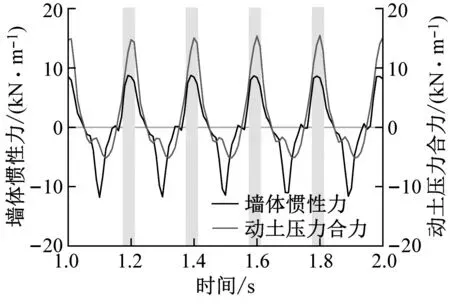
小震0.11g作用下，填土未加筋和填土加筋模型的墙体惯性力与动土压力合力时程曲线对比分别如图13(a)和图13(d)所示。由图可知，挡墙处于最不利位移状态时，墙体惯性力达到局部正峰值，未加筋模型的墙体所受动土压力合力同时达到局部正峰值，二者基本同步。然而，在填土加筋模型中，墙体惯性力最大时，动土压力合力却未处于正峰值处，二者存在明显的相位差。与小震类似，中震0.24g作用下，未加筋模型和加筋模型中惯性力与动土压力合力的对比分别如图13(b)和图13(e)所示。同样地，填土加筋措施使得墙体惯性力与动土压力合力存在显著不同步，表现出时间相位错峰。大震0.39g作用下，墙体惯性力与动土压力合力的时程曲线对比,如图13(c)和图13(f)所示。可以发现，2组模型的墙体惯性力与动土压力合力均同步运动，即墙体惯性力正峰值时，填土作用在墙背处的动土压力也最大，挡墙处于一种土推墙的危险状态。

(a) 未加筋模型，加载加速度=0.11g

(b) 未加筋模型，加载加速度=0.24g

(c) 未加筋模型，加载加速度=0.39g

(d) 加筋模型，加载加速度=0.11g

(e) 加筋模型，加载加速度=0.24g

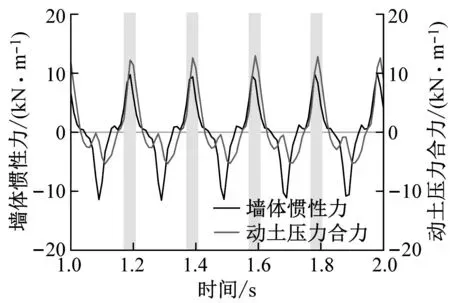
(f) 加筋模型，加载加速度=0.39g图13 不同加载幅值下墙体惯性力和动土压力合力的对比Fig.13 Comparison of time history of wall inertial force and dynamic earth thrust at different base acceleration

总体而言，悬臂式挡墙填土未加筋时，墙体承受的地震惯性力峰值和地震土压力峰值基本同步，与加载幅值的大小无关；填土加筋后，在小震及中震作用下，即墙体惯性力与动土压力合力并非同一时刻达到正峰值，这对于挡墙的稳定是更有利的。产生这一现象的可能原因是，填土加筋后墙-土系统的整体性提高，小、中震激励时，振动能量较小，加筋土体可近似看作块体结构，各高度处的填土与刚性墙背并非完全同一时刻相互作用；而大震作用下，加筋土体在较大惯性力驱动下，各高度处填土同一时刻推挤墙体，导致墙体惯性力和动土压力峰值基本同步。

最不利位移状态时墙体惯性力与动土压力合力的比值η，在0.11g、0.24g、0.39g加载下，未加筋模型的η分别为3.2、1.73、0.56，加筋模型的η分别为36.8、30.3及0.75，η呈现出随振动强度的增大而减小的规律。表明小、中震下，墙体惯性力为影响悬臂式挡墙稳定的主要荷载，而大震时，动土压力合力大于墙体惯性力，需重点考虑动土压力的不利影响。填土加筋后，在小震及中震作用下，η显著增大，这是由于惯性力与动土压力存在相位差，挡墙处于最不利位移状态时，填土作用在墙背上的动土压力非常小。

2.4.2 动土压力大小及分布

(1) 动土压力沿墙高分布

由于台面是周期性振动，提取图13中墙体惯性力达到峰值的任一时刻所对应各测点的动土压力数据，并绘制沿墙高分布如图14所示。由图14可知，动土压力沿高度呈非线性分布，小震及中震下，2组模型的动土压力均在零附近波动，填土加筋后挡墙上部甚至出现土压力负值，表明相对初始状态存在“卸载”效应，这是由于加筋填土整体性更好，填土未能及时跟随悬臂板朝临空侧运动。

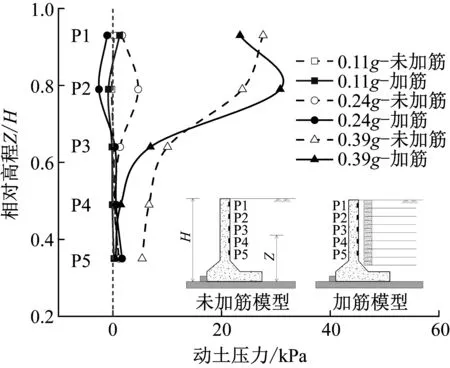
图14 最不利状态下动土压力对比Fig.14 Comparison of dynamic earth pressure at the most unfavorable condition

0.39g加载下，2组模型中填土作用在墙背的土压力增量均显著增加，沿高度大致呈“上部大下部小”的非线性分布，与M-O拟静力法中“上小下大”三角形线性分布有所差异。填土加筋后，大部分测点的动土压力均有所减小，仅个别测点动土压力偏大，可能是存在测试偶然误差，但总体上动土压力是减小的。填土加筋前后的动土压力合力作用点位置分别为0.71倍、0.79倍墙高，均高于拟静力法的1/3倍墙高。填土加筋与否对动土压力沿墙高的分布形态及合力作用点位置影响较小。

(2) 动土压力合力

动土压力合力对挡墙的稳定和安全至关重要。最不利位移状态时，在不同加载幅值作用下2组模型挡墙墙背的动土压力合力及相应的减载率,如表6所示。其中，减载率是填土加筋后动土压力合力的减小百分比。

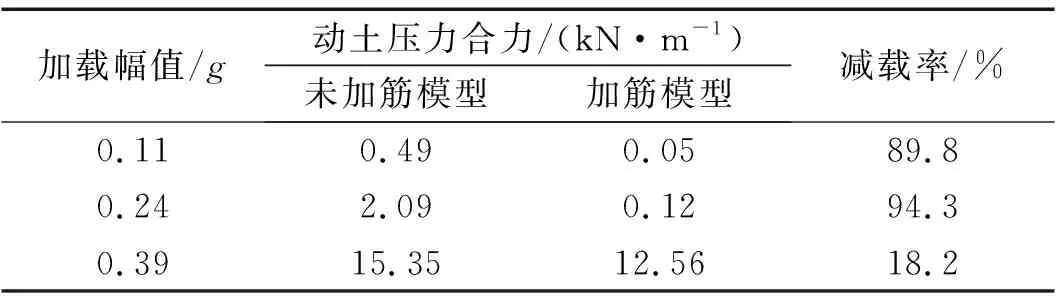
表6 最不利状态下动土压力合力及减载率Tab.6 Dynamic earth thrust and isolation efficiency at the most unfavorable condition

由表6可知，随着加载幅值的增大，2组模型中墙背受到的动土压力合力值均持续增大，并呈非线性加速增大的趋势，大震作用下的动土压力合力显著大于小、中震工况。Koseki等[38]认为这是由于填土内部产生应变局部化及土体强度衰减，导致土压力的快速增加。

填土加筋后，填土作用在墙背的动土压力合力值均有所减小，小震、中震及大震激励下，动土压力合力的减载率分别为89.8%、94.3%及18.2%，进而提高了挡墙的动力稳定性。尤其在小震及中震下，填土加筋会导致墙体惯性力和动土压力存在“错峰效应”，使得挡墙稳定最不利状态时动土压力急剧下降。尽管大震时，墙体惯性力和动土压力基本同步，但动土压力的合力值仍然减小了18.2%，这是由于加筋后土体强度有所提高。

3 结 论

设计并完成缩尺比为1∶4的墙后填土加筋与未加筋悬臂式挡墙振动台模型试验，采用低幅值高斯白噪声和幅值为0.11g(小震)、0.24g(中震)、0.39g(大震)的正弦波激励模型结构，测试并对比了2组模型的动力特性及其响应差异，分析了悬臂式挡墙填土加筋的减震效应特征，得到以下结论：

(1) 填土加筋可增强悬臂式挡墙-填土体系的整体性，降低地震造成的损伤。试验表明，随着地震动强度的增加，反映模型动力特性的自振频率和阻尼比分别呈减小和增大的变化趋势，结构损伤逐渐累积，并且加筋模型的自振频率降幅和阻尼比增幅均较未加筋模型更小，尤其是对伤损程度较为敏感的阻尼比增幅，前者仅为后者的32.6%～74.6%。

(2) 悬臂式挡墙体系的振动位移随加载幅值增加呈非线性增大，且填土位移逐渐超过墙体，加筋措施对墙-土位移的抑制效果与振动幅值密切相关。试验表明，小震下的填土位移较小，2组模型的振动位移差异不大；中震下，墙-土振动较大，加筋的减震效应发挥明显，墙顶和填土平均位移分别减小40.8%、17.7%；大震时，存在填土追挤墙体现象，加筋抑制填土位移效果发挥欠充分。

(3) 悬臂式挡墙填土加筋可导致墙体所承受地震惯性力与地震土压力存在相位差，大幅降低最不利位移状态时墙体所受地震土压力。试验表明，未加筋模型中墙体惯性力与地震土压力基本同步，填土加筋后小震及中震下的二者同步性明显降低，使得最不利位移状态对应的地震土压力减载率分别达到89.8%、94.3%，而在土追墙效应显著的大震下，地震土压力仍能减小18.2%。

填土加筋效应的发挥程度与筋-土之间的差异变形密切相关，可考虑在刚性悬臂板与加筋土体之间设置缓冲协调变形层，使得加筋体变形充分，进一步提高强震作用下悬臂式挡墙填土加筋的减震效应。