基于滞回非线性基座结构的舰船低频线谱重构试验研究
2022-10-17武国勋贾星光王嘉瑞姚熊亮
武国勋, 贾星光, 张 宇, 王嘉瑞, 姚熊亮
(1. 哈尔滨工程大学 青岛哈尔滨工程大学创新发展中心, 山东 青岛 266400; 2. 哈尔滨工程大学 船舶工程学院, 哈尔滨 150001)
舰船作为一个复杂的多设备激励系统,包括动力系统在内的大部分机械装置都具有周期性运动的工作特点。这些设备在工作时会产生较强的低频线谱并通过基座结构输出到船体结构中,从而导致由船体结构振动产生的水下辐射噪声部分会带有与舰船上各种激励源相关的线谱特征[1]。研究结果表明,各类水下和水面舰船低频段中的若干线谱或窄带辐射声是辐射噪声的主要特征[2],也是现代被动声纳在水声对抗中检测、跟踪和识别目标的主要特征信号[3]。因此随着舰船噪声控制水平的进步以及各种声学探测设备探测能力的提升,舰船线谱噪声尤其是低频线谱噪声的控制问题已成为舰船声隐身技术提升的重要制约因素。目前工程应用上主要有隔振、吸振、结构优化设计等以声学控制方法为主的被动控制措施,这些措施对于中高频段的线谱噪声降低有较好效果,而对于舰船的低频线谱噪声控制效果并不明显,无法有效的阻隔低频能量向外传递[4]。因此,各类主动控制措施被广泛研究用以控制低频线谱噪声,杨铁军等[5]对设计的MIMO自适应控制器应用多误差x-RLMS算法,通过仿真研究分析了其对双层隔振系统耦合振动的主动控制。李彦等[6-8]采用窄带Fx-Newton算法,提出了窄带滤波相位差的自适应补偿环节,通过磁悬浮作动器来实现低频线谱的控制。方昱斌等[9-10]以Fx-LMS算法为基础,分别提出了混合自适应主动控制方法以及应用基于Halbach的新型作动器来控制目标频谱的振动。Hu等[11-12]提出了一种基于接收点位置估计的船舶航行噪声低频线谱主动控制方法,能够利用次级声源实现低频线谱的有源抵消。此外,还有学者研究了通过强非线性引发系统混沌实现线谱混沌化的方法。Liu等[13]利用非线性隔振系统发生混沌时响应谱连续的特征,设计了非线性反馈控制器用于消除或减小辐射噪声线谱。杨庆超等[14]利用开环加非线性闭环耦合方法研究了两自由度非线性隔振系统的吸引子迁移和线谱混沌化。Jiang等[15-16]分别建立了混沌隔振系统与磁流变悬架动力学系统,发现了系统由周期分岔逐渐变为混沌状态,线谱由单谱转变为宽带谱的可能性。Lou等[17]从试验的角度比较了混沌和非混沌状态的线谱衰减和振动抑制,证明了混沌状态下的非线性隔振系统具有线谱抑制能力。Zhou等[18]提出了一种可用于线谱重构的频谱优化方法,通过遗传算法使目标函数最小化,从而将简谐振动的线谱转化为混沌运动的宽带连续谱并验证了两自由度线性机械系统混沌化的有效性。
为丰富舰船振动噪声线谱重构方法,本文提出一种含半主动作动单元——MRD(magnetorheological damper)的滞回非线性基座结构。MRD的滞回非线性特性在特定条件下会引发舰船基座出现跳跃、多映射等独特的非线性特征,甚至可使结构出现混沌态运动,这为舰船振动噪声的低频线谱特征重构奠定了基础。除理论分析与数值计算,本文还开展了缩比模型试验,通过试验分析验证了装置的在结构振动低频线谱重构中的有效性。
1 基座力学模型及动力学特性分析
1.1 滞回非线性基座结构力学模型
不同于传统舰船基座结构,滞回非线性基座引入了MRD这一半主动作动元件,如图1所示。MRD的引入赋予了基座结构非线性力学特征,这是利用其实现舰船振动线谱重构的基础。滞回非线性基座物理模型如图2所示。MRD力学模型由经典的Bouc-Wen模型描述。为分析滞回非线性基座的非线性动力学特性,采用单自由度系统建立滞回非线性基座的数学模型[19]
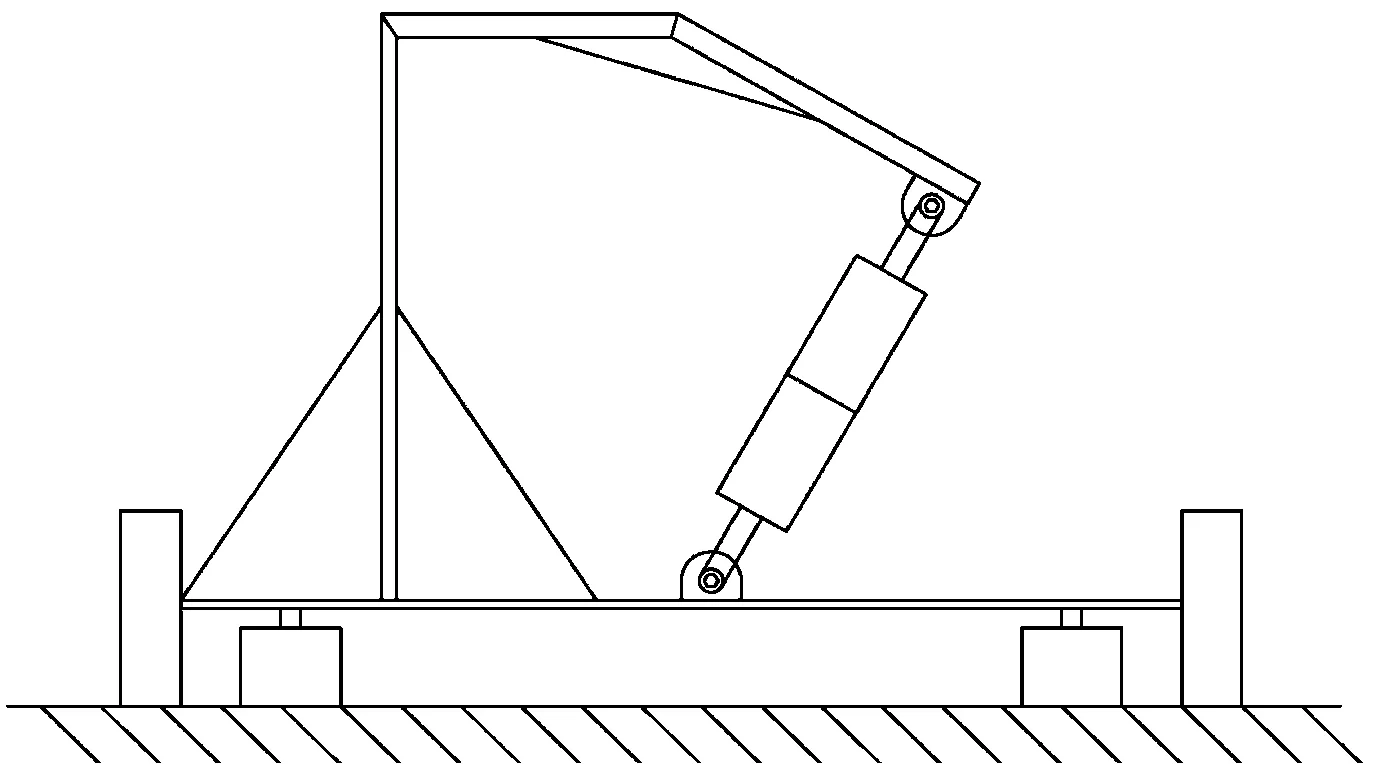
图1 滞回非线性基座结构Fig.1 Schematic diagram of hysteretic nonlinear base structure
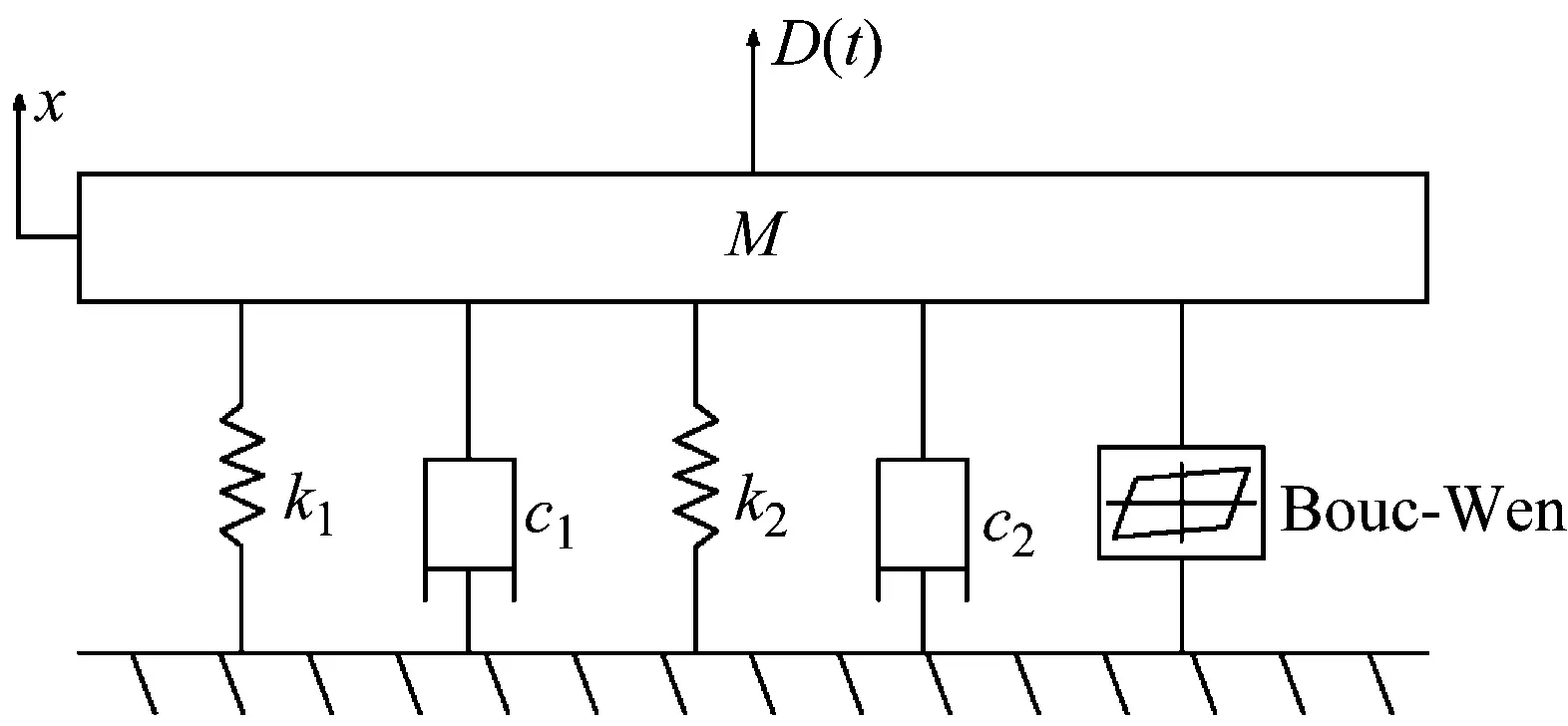
图2 滞回非线性基座结构物理模型Fig.2 Mechanical model of hysteretic nonlinear base structure
(1)
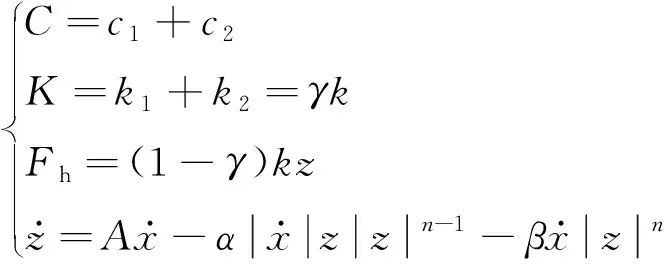
(2)
式中:c1、c2分别为基座结构、MRD的阻尼;k1、k2为两者刚度;γ为屈服前后的刚度之比;k为初始线性刚度;z为无单位渐进变量;A、α、n、β为MRD的滞回参数。
1.2 滞回非线性基座结构力学模型
将式(2)代入式(1)进行化简,并引入变量ζ=C/2Mω、ω2=k/M、u(t)=D(t)/M,建立了滞回非线性基座结构振动微分方程为
(3)
令滞回非线性基座结构所受的简谐激励力为u(t)=Bcos(2πpt),取滞回参数n=1,则式(3)变化如下
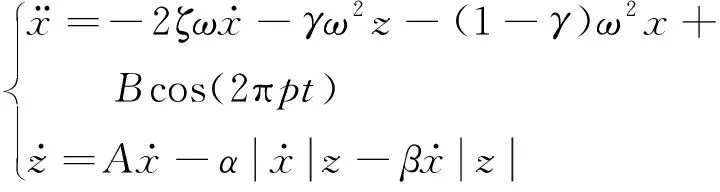
(4)
式中:ζ为单自由度系统的阻尼比;ω为系统固有频率;B为简谐激励的幅值;p为简谐激励的频率。
为分析滞回非线性基座的非线性动力学特性,开展数值模拟。令式(4)中初始时刻滞回非线性基座结构的速度与位移为零,取A=1.0,ω=1.0,ζ=0.02,γ=0.5,p=1/2π,对于选定的α、β调节激励幅值B的大小,提取滞回非线性基座结构不同激励幅值下系统的运动速度并绘制分岔图。如图3所示。滞回非线性基座结构力学模型的激励幅值-振动速度曲线中存在明显的分岔现象,且随着|α/β|的增大,系统的振动速度分岔图中发生混沌的面积逐渐减少。以图3(a)中曲线为例,随着激励幅值B的增大,滞回非线性基座结构系统的速度曲线逐渐发生分岔,当15≤B≤17、24≤B≤26时系统短暂进入混沌运动,当B≥30后系统大面积发生混沌运动。
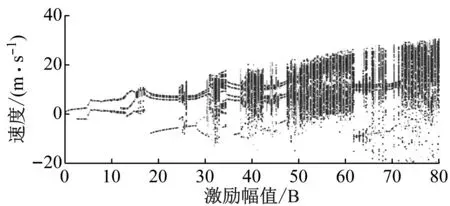
(a) α=0.05、β=-0.95
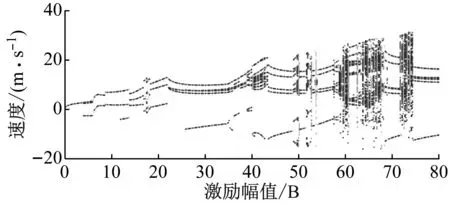
(b) α=0.20、β=-0.80
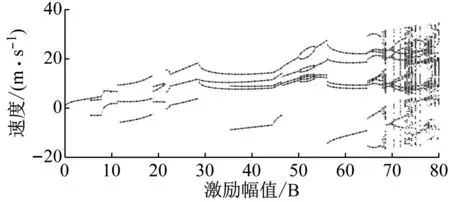
(c) α=0.30、β=-0.70图3 基座结构力学模型运动速度分岔图Fig.3 Bifurcation diagram of motion velocity for mechanical model of base structure
对图3(a)中曲线进一步分析,将激励幅值B在分岔区间段内取值进行混沌分析,作混沌相图。如图4所示。滞回非线性基座结构力学模型的振动相图中存在明显的混沌吸引子,且输入幅值B越大,混沌现象越明显。这从理论上说明了滞回非线性基座结构力学模型中可以引发混沌现象。
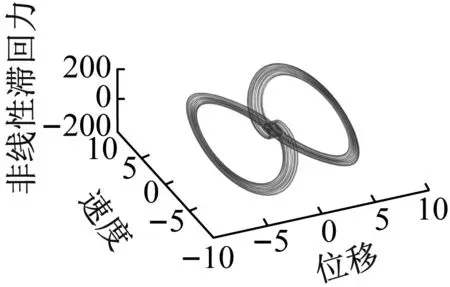
(a) B=17
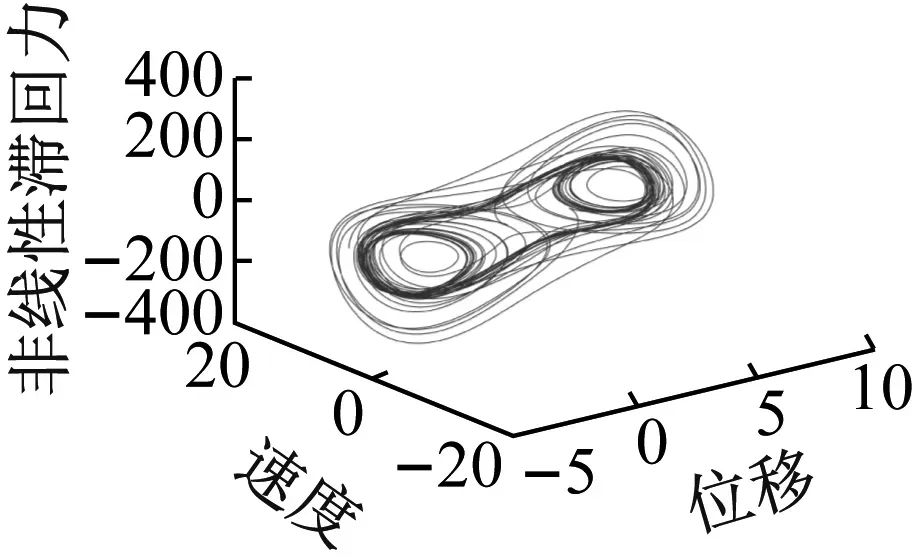
(b) B=26
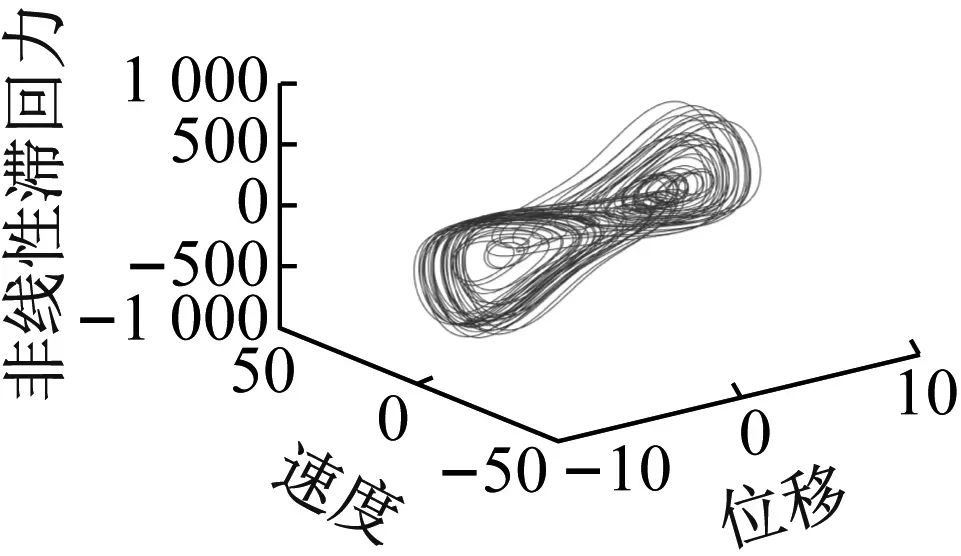
(c) B=55
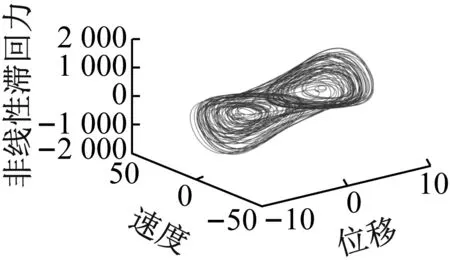
(d) B=80图4 基座结构力学模型混沌相图Fig.4 Chaotic phase diagram of mechanical model of base structure
2 舰船低频线谱重构试验验证
根据动力学特性数值分析结果,滞回非线性基座能够产生分岔、混沌等典型非线性运动状态,这是实现舰船振动线谱重构的基础,为进一步验证滞回非线性基座的低频线谱重构能力。本节将对某型舰艇上实际应用的小型设备基座结构进行简化并按比例缩小。在此基础上引入MRD,制作出新型的滞回非线性基座结构缩比模型,如图5所示。并搭建试验平台开展舰船低频线谱重构试验。

图5 基座缩比模型结构实物图Fig.5 Physical drawing of base scale model structure
基座缩比模型安装于实验台架上,其形式不同于传统典型基座结构,因MRD的阻尼力输出以阻尼器活塞的振动速度和位移为前提,试验时为了使MRD输出满足要求的阻尼力,采取了加长基座面板的方法对基座结构进行优化。基座缩比模型结构包括腹板、面板、肋板以及磁流变阻器(型号RD-8040-1)。结构尺寸如表1所示。
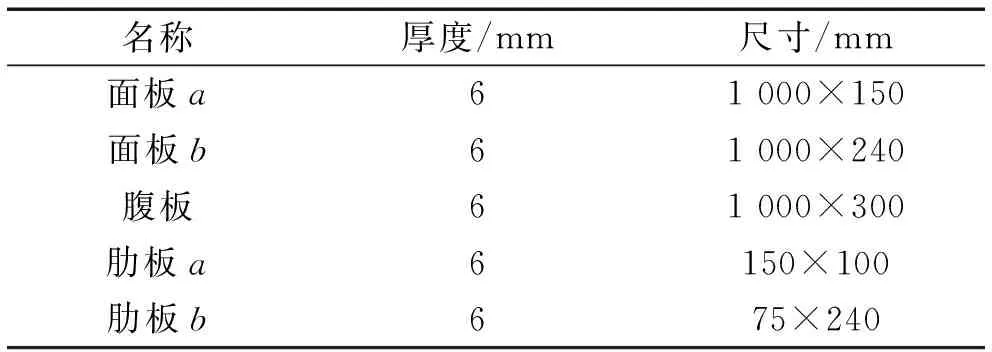
表1 基座缩比模型结构尺寸Tab.1 Structural dimension of base scale model
在试验中,采用SINOCERA JZK-50型激振器作为振源,可于基座面板处施加不同频率的简谐激励,将PCB加速度传感器布置于面板及底板不同部位用于测量振动信号,并通过NI PXI-1045数据采集仪进行采集,用可编程电源调节MRD输入电流的大小,试验装置如图6所示。

图6 基座缩比模型结构试验系统Fig.6 Test system of base scale model structure
2.1 基座缩比模型结构固有频率试验
为研究MRD不同输入电流工作状态对基座缩比模型结构固有频率的影响,选取MRD输入电流为0、1 A、2 A,在不同输入电流下进行基座缩比模型结构固有频率试验,通过力锤敲击基座面板,对采集到的时域信号进行FFT(fast Fotcrier tramsform)变换,频域结果如图7所示。
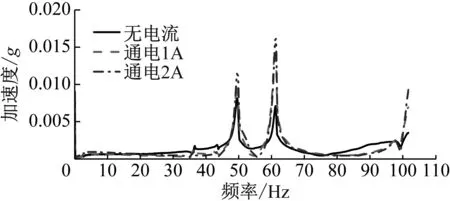
图7 固有频率试验结果Fig.7 Test results of natural frequency
基座缩比模型结构在100 Hz以下频段内其频响曲线存在两个峰值点,分别对应结构的前两阶固有频率:一阶固有频率在不同输入电流下均约为49.5 Hz;二阶固有频率在不同输入电流下均约为61.5 Hz。由此可见输入电流的变化对于基座缩比模型结构的前两阶固有频率没有影响。试验结果表明,滞回非线性基座引入电流调节控制后,并不改变基座固有频率等结构固有属性。
2.2 基座缩比模型结构线谱重构试验
试验时会有两个输入条件对滞回非线性基座结构的线谱重构效果产生影响,分别是激振器的激振频率以及阻尼器的输入电流,为研究这两种因素对此基座线谱重构效果的影响,选定了不同的激振频率及输入电流组合进行基座缩比模型结构线谱重构试验,各种工况组合如表2所示。
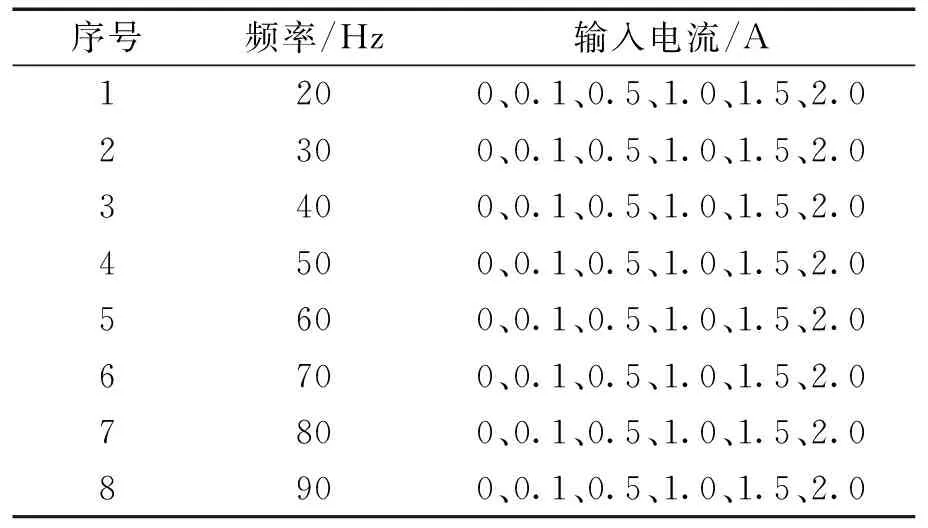
表2 线谱重构试验工况组合Tab.2 Combination of Test conditions for line spectrum reconstruction
将试验结果进行汇总整理,重点关注面板b上位于MRD上方的测点振动信号,提取此测点处所有工况下激振频率对应线谱峰值对应的振动加速度,如图8所示。
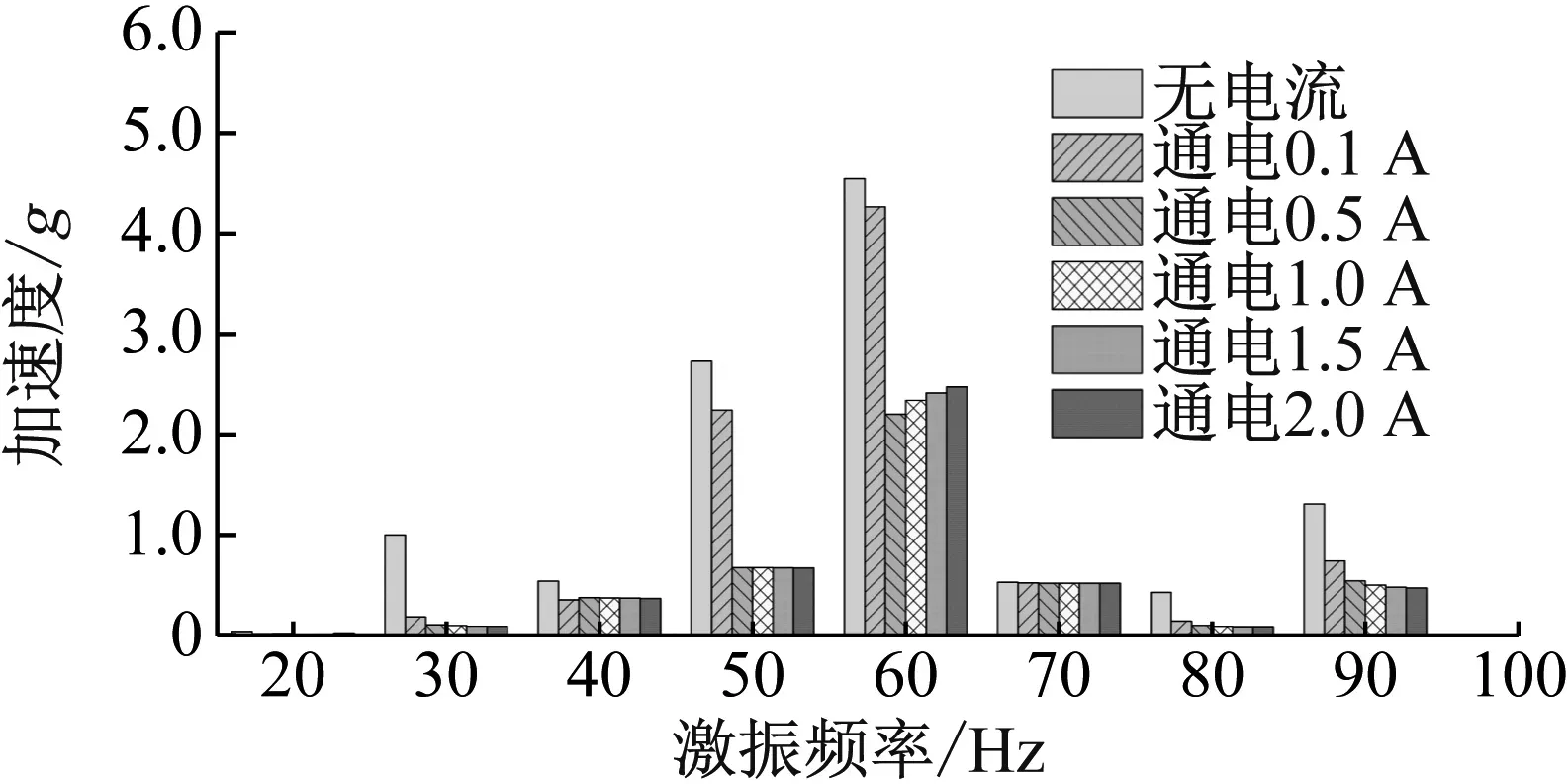
图8 线谱重构试验结果Fig.8 Test results of line spectrum reconstruction
在100 Hz以下频段内,相较于无电流工况,MRD在不同输入电流工作状态下均能降低激振频率线谱峰值,此外50 Hz与60 Hz处于基座试验模型的共振频率附近,其振动响应较其他频率点处更为强烈,线谱抑制效果也更明显,当输入电流为0.5 A时,在50 Hz激振频率工况下线谱峰值降低了75.12%,60 Hz激振频率工况下线谱峰值降低了51.52%。
(1) 在研究阻尼器输入电流对滞回非线性基座结构振动响应线谱特征的影响时,需选定同一激振频率下,不同输入电流的工况组合进行分析。由上文可知此基座试验模型一阶固有频率约为49.5 Hz,因此选取4号工况组合来进行基座一阶固有频率附近的振动响应线谱特征分析,验证滞回非线性基座结构的低频线谱重构现象,并分析输入电流大小对线谱重构效果的影响。作50 Hz激励频率下不同输入电流的信号曲线(稳态状况3 s),如图9所示。
(a) I=0与0.1 A
(b) I=0与0.5 A
(c) I=0与1.0 A
(d) I=0与1.5 A图9 不同输入电流对振动的时域影响Fig.9 Time domain effects of different input currents on Vibration
为得到不同工况下振动数据的有效值,将图9中时域曲线数据取均方根处理,并比较通电工况相较于无电流工况的均方根值降低幅度,如表3所示。
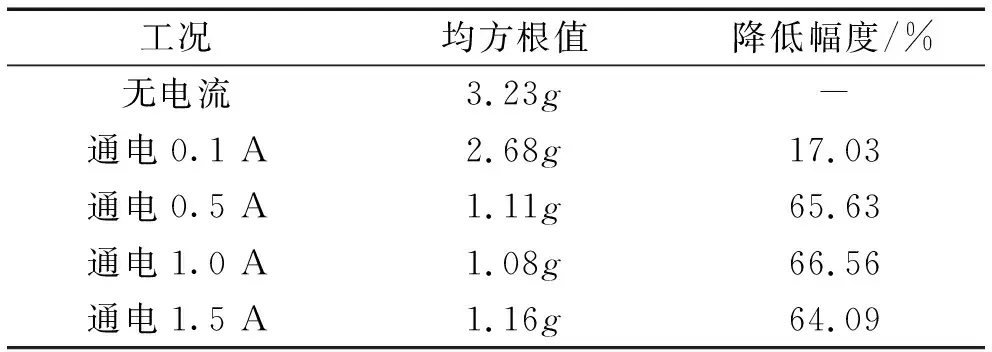
表3 不同输入电流对振动幅值的影响Tab.3 Influence of different input current on vibration amplitude
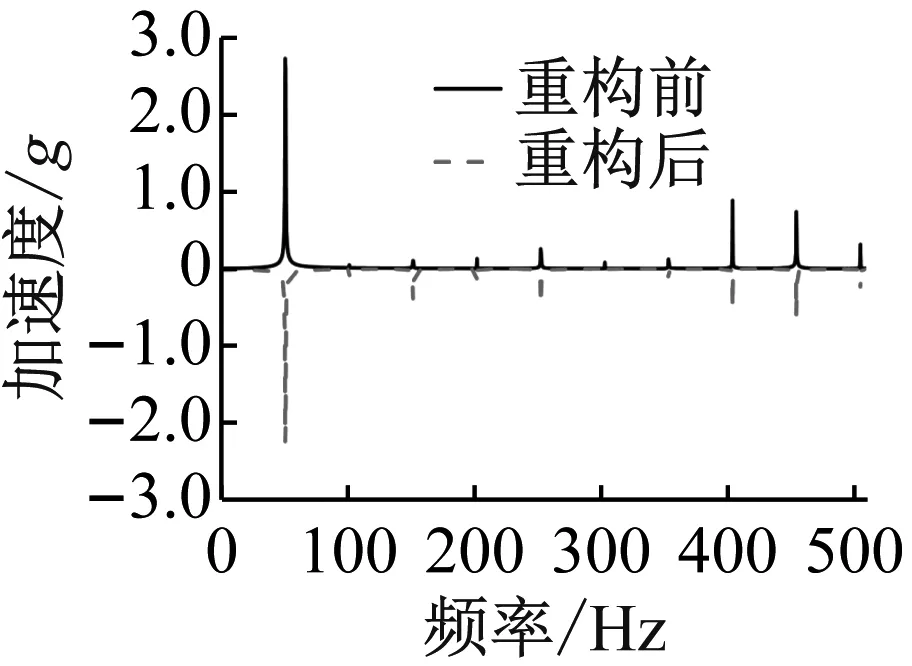
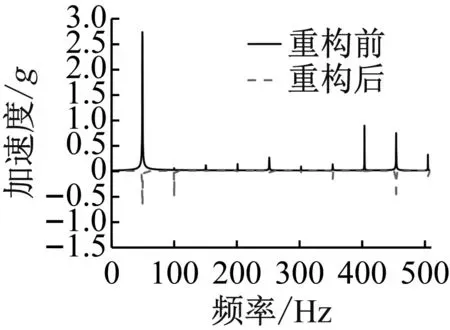
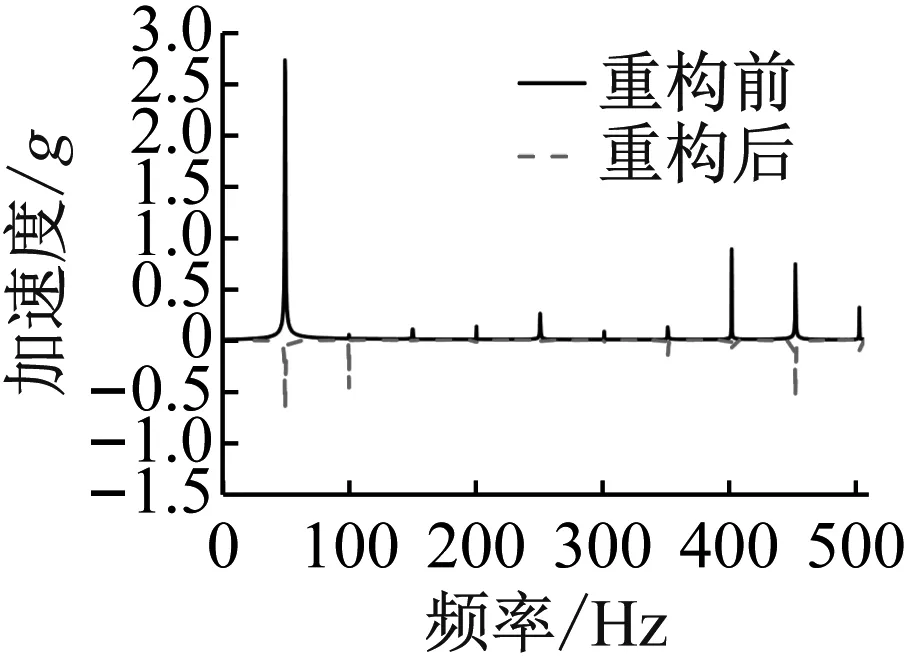
在稳态振动情况下,MRD引入后可以降低振动幅值,且随电流的增大,幅值降低越明显,但通电0.5 A、1.0 A与1.5 A三组工况降低幅度相近,可以表明对于此基座结构通电0.5 A左右即可达到较好的振动抑制效果,为研究其对线谱控制的效果,作频响曲线如图10所示。
(a)I=0与0.1 A
(b) I=0与0.5 A
(c)I=0与1.0 A
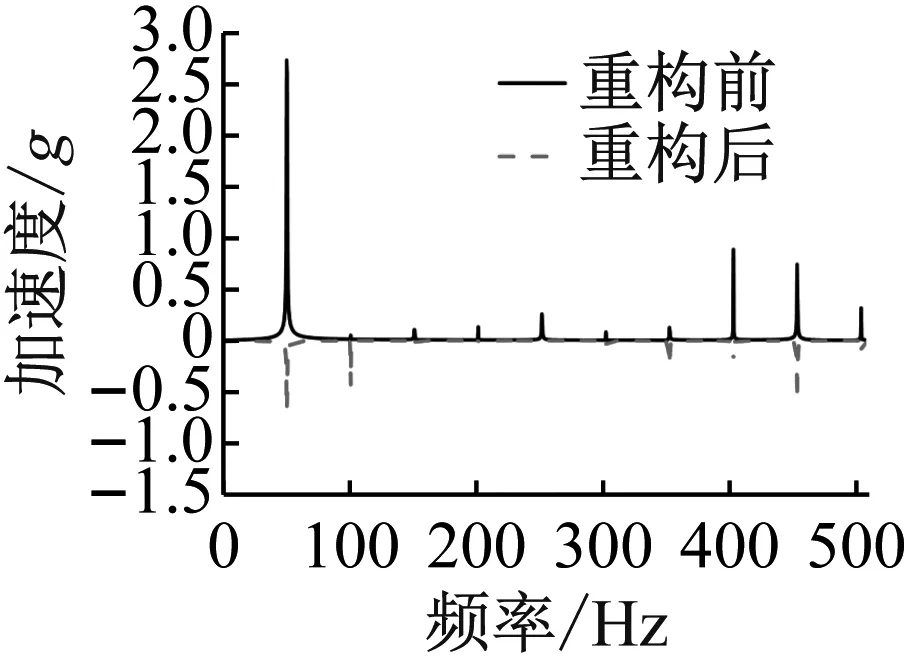
(d) I=0与1.5 A图10 不同输入电流对振动的频域影响Fig.10 Frequency domain effects of different input currents on Vibration
读取图10中不同输入电流下各线谱峰值大小及对应频率,可以发现在50 Hz激振频率下,重构前(无电流)频响曲线会在50 Hz处产生较高的强迫振动线谱峰值,此外在如101 Hz、151 Hz等倍数频率处也会产生峰值响应,但激励频率线谱成分更为明显,很容易通过这一线谱特征分析出设备激励特点,不利于舰船声隐身性。重构后(通电工况)激振频率对应线谱峰值会大幅降低,且在0~0.5 A范围内,电流越大线谱重构效果越明显,在输入电流为0.5 A工况下,线谱有三个较明显频率成分分别为50 Hz、101 Hz及454 Hz,其线谱峰值分别对应0.68、0.51及0.56,三者相差不大,并无明显线谱特征,当此线谱被监测到时不能轻易由此确定设备激励特点,从而利于舰船声隐身性能。当输入电流超过0.5 A范围时,重构后的线谱相较于通电0.5 A工况线谱并无明显变化。因此,根据时频域振动响应结果分析,可以得出如下结论:MDR输入电流大小会对滞回非线性基座线谱重构效果产生影响,表现为在0~0.5 A范围内,输入电流越大,线谱重构效果越明显,当输入电流继续增大时,线谱重构效果与通电0.5 A工况差别不大。
(2) 为研究滞回非线性基座结构在不同频率下的线谱重构效果,需选定相同输入电流下,不同激振频率的工况组合进行分析。选取输入电流0.5 A工况与无电流结果进行对比,研究激振频率对滞回非线性基座振动响应线谱特征的影响,作各激振频率下频率-响应幅值曲线如图11所示,为研究线谱重构效果,读取各激振频率对应的线谱峰值,并比较其重构后激振频率线谱峰值降低幅度,如表4所示。
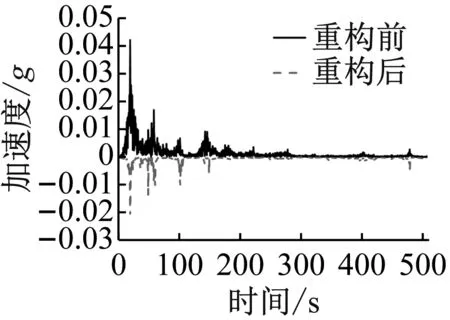
(a) 激励频率20 Hz
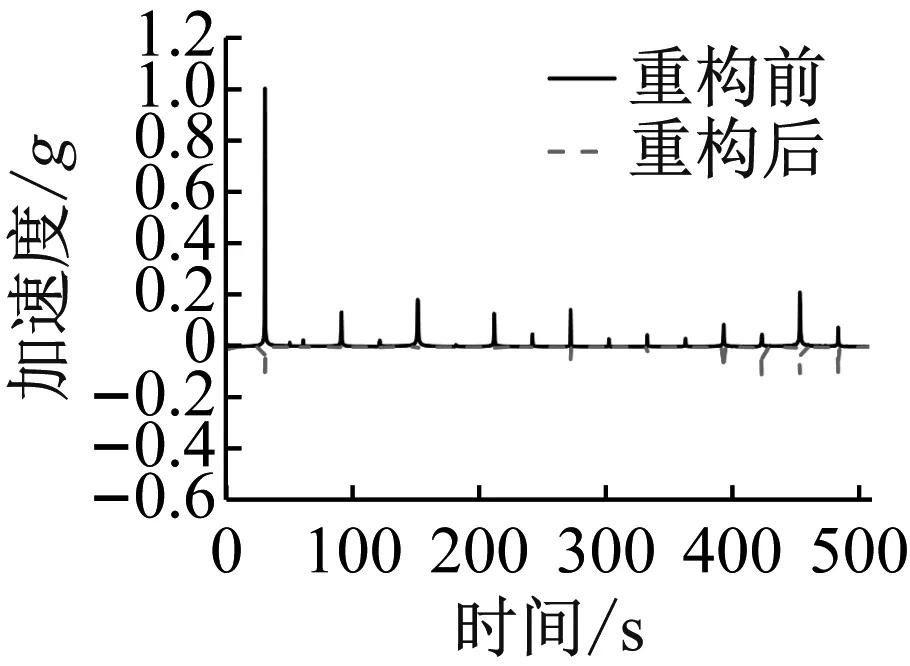
(b) 激励频率30 Hz
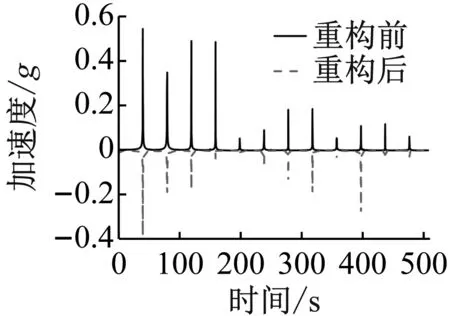
(c) 激励频率40 Hz
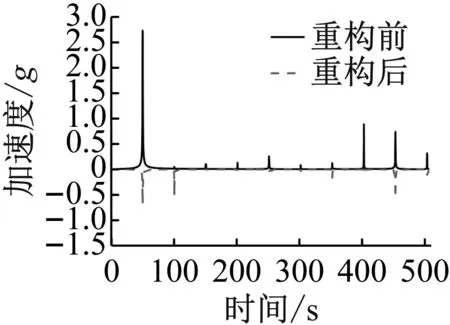
(d) 激励频率50 Hz
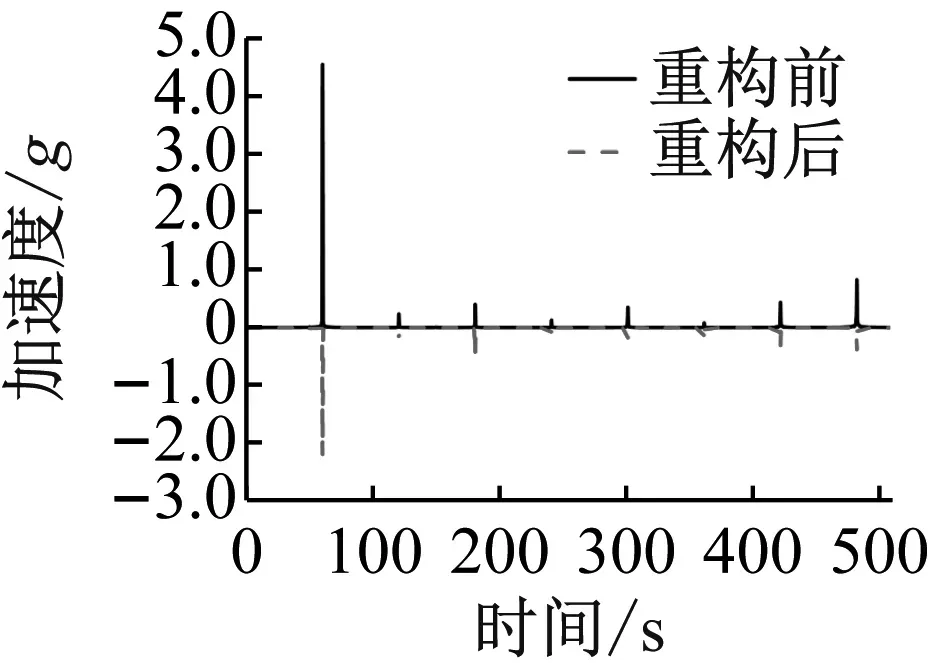
(e) 激励频率60 Hz
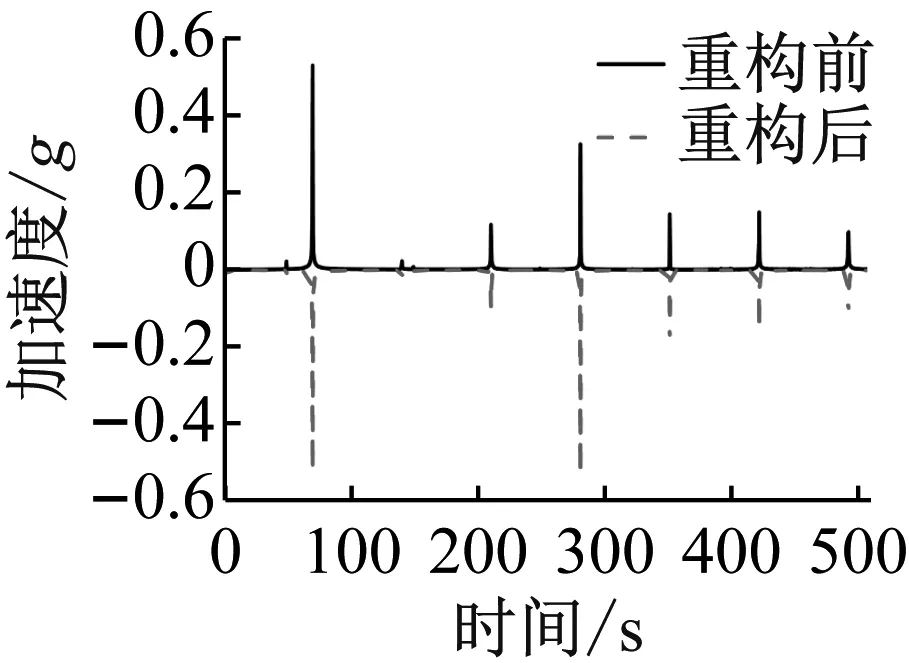
(f) 激励频率70 Hz
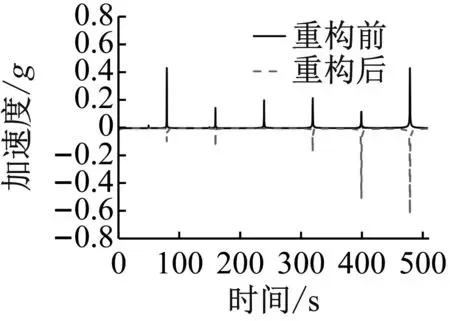
(g) 激励频率80 Hz
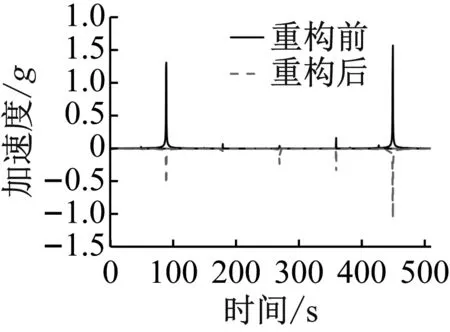
(h) 激励频率90 Hz图11 激振频率对线谱重构影响Fig.11 Influence of excitation frequency on line spectrum reconstruction
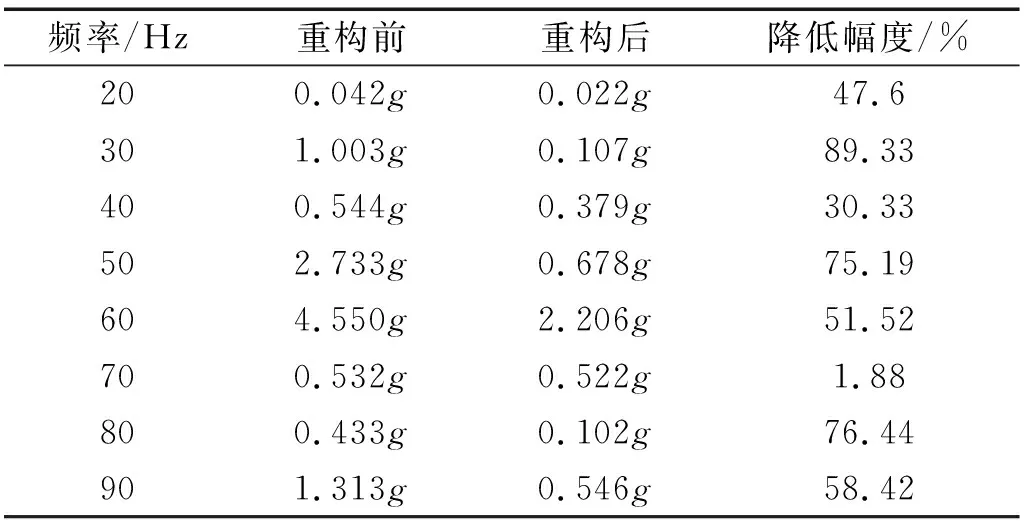
表4 各激振频率下线谱峰值Tab.4 Peak value of line spectrum at each excitation frequency
由表4可以发现,对于输入电流为0.5 A时,激振频率为30 Hz、50 Hz及80 Hz工况,重构后激振频率线谱峰值能降低75%以上,最大为89.33%。观察图11中各线谱重构情况可以发现:对于激振频率为30 Hz、70 Hz、80 Hz的工况而言,线谱重构后不仅对激振频率线谱峰值产生抑制,重构后的线谱其高频部分谱峰值明显升高,甚至超过激振频率谱峰值占据主导地位,实现了振动能量从低频向高频的转移。如激振频率为80 Hz工况下,重构前线谱其80 Hz对应谱峰值大小为0.433,而高频部分的400 Hz谱峰值为0.120,480 Hz谱峰值为0.431;重构后线谱高频部分的400 Hz谱峰值达到了0.503(增大319%),480 Hz谱峰值达到了0.615(增大42.7%),而80 Hz对应谱峰值仅为0.102(减小76.4%),线谱中描述激振频率的特征线谱被大大降低,不再占据较高成分,有很好的线谱重构效果,利于舰船声隐身性能。对于激振频率为40 Hz、50 Hz的工况而言,线谱重构后除对激振频率谱峰值产生抑制外,部分高频线谱峰值增大,其谱峰值与激励频率对应谱峰值相当,实现了线谱均匀化,如激振频率为40 Hz工况下,重构后40 Hz对应谱峰值为0.370,400 Hz对应谱峰值为0.274,两者相差不大。对于激振频率为20 Hz、60 Hz、90 Hz的工况而言,线谱重构后可以对激振频率谱峰值产生抑制,但其线谱特征与重构前比较相似,占据主导成分的线谱其对应频率并未发生改变。
3 结 论
本文提出了滞回非线性基座结构形式,并进行了数值仿真及基座缩比模型试验验证其对低频线谱的线谱重构效果。试验结果显示:
(1) 滞回非线性基座引入电流调节控制后,会产生线谱重构现象,但不会改变基座固有频率等固有属性。
(2) 对试验缩比模型而言,在0~0.5 A范围内调节输入电流的大小,线谱重构的效果会随电流的增加而更加明显,在达到最佳控制电流后,即使电流继续增大,线谱重构效果也不会有明显差异。
(3) 线谱重构不仅会对特征低频线谱产生抑制,还会增大高频谱峰值,从而使线谱特征发生改变。这实现了振动能量从低频向高频的转移,而高频振动对于现代舰船隐身性能而言影响较小,且较易治理。
