湿热环境下反对称正交铺设双稳态扁壳的建模与非线性振动响应研究

张博宇， 张 伟

(北京工业大学 材料与制造学部机械结构非线性振动与强度北京市重点实验室，北京 100124)

双稳态结构是由多层纤维增强材料铺设而成，是具有两种不同稳定状态的复合材料层合结构。在机械力、智能材料、温度场等外载荷驱动下，可由一种稳态转变为另一种稳态，并且无需持续的能量输入即可维持稳定构型。Hyer[1]最早发现非对称正交铺设圆柱壳结构具有双稳态特性。Daton-Lovett[2]发现反对称铺设的复合材料圆柱壳结构也能够呈现出规则圆柱状的两种稳态，引起了国内外诸多学者的广泛关注。双稳态复合材料结构作为基础制造而成的产品在实际使用过程中不可避免地会受到周围变化的环境(例如温度和湿度等)的影响，使双稳态复合材料结构加工成型后不同稳态的结构形状尺寸以及不同稳态间的稳态转变过程发生改变，使得近年来众多学者对温度和湿度对双稳态复合材料结构的影响进行研究。

复合材料从应用性质可分为功能和结构复合材料两大类。功能复合材料主要具有特殊功能，目前已在航空航天、船舶海洋、石油化工、机械工程等方面得到了广泛应用[3]。结构复合材料[4]是由增强物和基体组成，将增强材料按照一定方式加入到基底材料，具有明显的非均匀性和各向异性性质，从而克服单一材料性能的某些缺点，以获得具有特殊力学性能的一类新型材料。增强物起着承受载荷的主要作用，其几何形式有长纤维、短纤维和颗粒状物等多种。基体起着黏结、支持、保护增强物和传递应力的作用，常采用橡胶、石墨、树脂、金属和陶瓷等。

纤维增强复合材料是一种高功能材料，它在力学性能、物理性能和化学性能等方面都明显优于单一材料，表现出高比模量、高比刚度、耐磨损和耐腐蚀等特性。复合材料层合板强大的可设计性，为振动性能设计提供了极大潜力，使其在航空、航天和船舶等领域得到了广泛应用。在航空航天领域上，目前已经有越来越多的部件采用纤维增强树脂基复合材料层合结构，所以对复合材料层合结构的研究和开发已从单纯减轻重量角度，发展到了综合考虑减重、增加使用寿命和承载能力等多种复杂因素的层面。这些结构在使用过程中也会因各种实际复杂服役环境表现出各种非线性振动问题而影响设备的功能使用。振动问题产生的可能原因有结构设计缺陷、制造误差和安装误差等，所以有必要从复合材料层合结构振动特性的理论研究出发分析实际振动问题产生的本质机理。因此，研究复合材料层合板的振动特性工程意义极为重大，受到广大科学工作者的高度重视。

按照纤维增强复合材料层合板铺层方式，可将其划分为正交铺设、反对称铺设和一般角铺设三种类型。对于正交铺设复合材料层合板的研究，Harras等[5]研究了固支对称复合材料层合板的几何非线性自由振动，分析了非线性特性对共振频率和非线性低阶模态的影响。段纪成[6]讨论了正交各向异性层合板的弯曲与振动，建立了弯曲与振动的控制方程与边界条件。胡浩等[7]分析了几何非线性黏弹性正交各向异性对称铺设的层合矩形板的非线性动力响应问题，得到了含有时间变量的非线性微积分方程。Leung等[8]利用三阶剪切变形理论，研究了四边简支条件下对称铺设的复合材料层合板非线性动力学行为。Ye等[9]研究了正交对称铺设的复合材料层合板在参数激励作用下的非线性振动和混沌运动，用摄动分析法对系统进行分析，发现了系统的周期和混沌运动。Guo等[10-16]利用Reddy的高阶剪切板理论研究了二自由度和三自由度正交对称铺设复合材料层合板结构，受面外和面内激励联合作用的非线性动力学特性及全局动力学与混沌运动。

由于反对称铺设的复合材料层合结构常被应用在直升飞机旋翼的设计中，对其非线性振动特性的研究也在不断增多。Swaminathan等[17]用改进的高阶剪切板理论得到了反对称铺设复合材料层合结构静态分析的解析解。Huang等[18]研究了在湿热作用下剪切变形的反对称铺设复合材料结构的非线性振动和响应，用高阶剪切理论和von Karman变形理论，得到了系统的运动方程，分析了温度，湿度变化和非线性因素等对固有频率和振动响应的影响。Nath等[19]研究了弹性地基上反对称铺设复合材料方板受到横向连续载荷和阶跃载荷作用的静态和动态性能。Soula等[20]利用经典层合板理论、一阶剪切变形理论和三阶剪切变形理论研究了考虑阻尼影响的复合材料层合板的动力学特性。同年，Aagah等[21]利用三阶剪切变形理论研究了复合材料层合板的自由振动特性。Swaminathan等[22-23]用各种高阶剪切简化理论和数值模型对反对称角铺设复合材料层合板进行了静力分析。Swaminathan等[24]又用高阶剪切变形理论计算了反对称角铺设复合材料层合板自由振动的固有频率，指出Reddy的高阶剪切理论得到的固有频率比实际值偏高。

对于一般非对称角铺设层合结构的动力学性能研究，Matsunaga[25-26]讨论了角铺设复合材料层合板的热屈曲问题并利用二维广义的高阶剪切变形理论研究了自由振动和稳定性问题。Weaver等[27]描述了非对称铺设复合材料层合板的大幅分叉现象，用[0°/90°]两层的复合材料板验证了发生大幅分叉过程中能量的传递和结构的变形情况。Guo等[28-29]研究了角铺设复合材料层合板在1∶1内共振情况下非线性振动的周期和混沌运动。Honda等[30]研究了短纤维和弯曲纤维增强复合材料层合板振动特性，考虑了由于短纤维引起的材料局部各向异性。

本文在经典壳理论的基础上，考虑温度和湿度的影响，建立了反对称正交铺设双稳态扁壳非线性动力学模型。再应用Galerkin方法对系统偏微分运动控制方程进行三阶离散，得到了双稳态系统在主共振Ω接近于ω1，内共振为1∶2∶2条件下外激励幅值变化对反对称正交铺设条件下双稳态系统的非线性动力学特性的影响规律。

1 反对称正交铺设双稳态扁壳的动力学控制方程

反对称正交铺设层合结构是由正交各向异性单层结构的材料主方向与坐标轴夹角成0°和90°交错铺设而成，刚度系数具有以下关系：(Q11)0°=(Q22)90°,(Q22)0°=(Q11)90°及Q16=Q16=0。因此有：A11=A22,A16=A26=D16=D26=B16=B26=0, 且可证明B12=B66,B22=-B11。选择4层[0°/90°/0°/90°]作为铺设方式，模型在激振器激发振动下可以得到两个稳定状态，如图1所示。使用玻璃纤维和环氧树脂基底作为制作材料，单层厚度为0.185 mm，其余材料参数如表1所示。

(a) 第一个平衡位置

(b) 第二个平衡位置图1 双稳态结构受激振器作用的模型图Fig.1 Model diagram of bistable structure under the action of exciter

表1 S1002单层材料参数Tab.1 Single layer material parameters of S1002

在经典层合壳理论的基础上，考虑湿热环境的影响，推导出湿热环境下反对称正交铺设双稳态壳的动力学控制方程。首先，在湿度和温度变化的环境中，单层壳材料主方向产生的应力为

(1)

式中:α为材料的热膨胀系数；β为材料的湿膨胀系数。

反对称正交铺设复合材料的内力N和内力矩M的表达式可写作如下形式

(2)

式中:Aij为面向内力与中面应变有关的刚度系数，统称为拉伸刚度矩阵；Bij为弯曲、拉伸之间的耦合刚度矩阵；Dij为内力矩与曲率及扭曲率有关的刚度系数，统称为弯曲刚度矩阵。

将式(1)代入式(2)中，可以得到

(3)

式中:NT、MT分别为由温度产生的热内力和热内力矩；NH、MH分别为由湿度产生的湿内力和湿内力矩。

(4a)

(4b)

则中面产生的应变和曲率可以表达为

(5)

其中，由温度和湿度产生的应变和曲率为

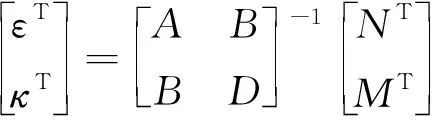
(6a)

(6b)

采用经典非线性扁壳理论和冯卡门大变形理论，应用Donnell圆柱壳中面的非线性几何方程

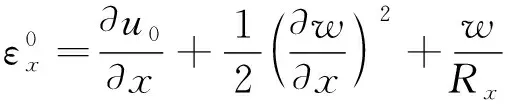
(7a)

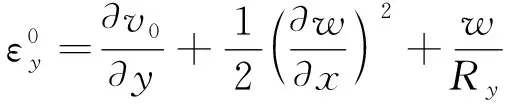
(7b)

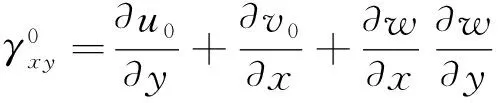
(7c)

式中:u0,v0,w分别为圆柱壳中面上的点沿x,y,z方向上的位移；Rx,Ry分别为圆柱壳沿x,y方向上的初始截面曲率半径。

由于扁壳振动的主要方向是横向挠度，因此忽略面内的惯性。由于几何方程中面内位移与横向位移之间存在耦合，故需引入相容方程以组成完整的方程组。平面应力状态下的双曲扁壳的相容方程表达式为

(8)

扁壳振动理论中独立的内力分量有六个：Nx、Ny、Nxy、Mx、My、Nxy，消去剪切力Nx、Qy后，可以得到3个动力平衡方程

(9a)

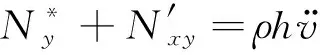
(9b)

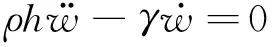
(9c)

式中:F为壳所受的外激励;γ为阻尼系数。3个内力分量Nx、Ny、Nxy，可用艾雷应力函数按下列方式加以联系

(10a)

(10b)

(10c)

将式(7)代入式(8)中，可使动力平衡方程式(9a)和式(9b)自动满足。再联立式(3)与式(10)，可求得用Pij表示的中面应变表达式

(11a)

(11b)

(11c)

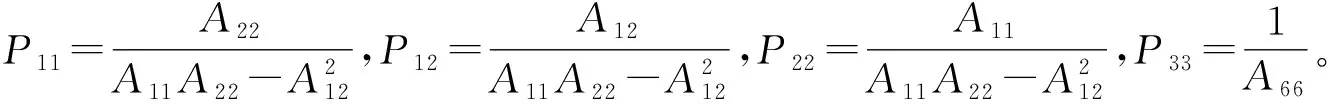
可知，此时面内、面外位移之间完成解耦，则非线性偏微分系统可以仅由横向位移w(x,y,t)和应力函数Φ(x,y,t)表示。再将内力和内力矩的简化式(2)和中面应变表达式(7)代入到动力平衡方程式(9c)中，可得

(12)

代入相容方程式(8)中可得

(13)

在模态叠加法的讨论中，连续系统的解可写作全部模态函数的线性组合。由于模型的边界条件为四边自由，中心固定支撑。因此，所选的形函数不需要满足任何几何边界条件，则沿z方向的位移形函数表示如下

(14)

式中,Wij(t)为广义坐标;wij(x,y)为系统的模态函数。下角标i=0,1，…，M，j=0,1，…，N，所有形函数项均为非零的三角函数的组合运算，其中M=4I+1，M×N即为近似时选取的自由度数。

由于所建模型为扁壳结构，且横向位移和应力函数所定义的区域相同，因此假定它们可以以相同的形函数wij(x,y)进行展开。取横向位移w、应力函数Φ的振型函数形式如下所示

(15a)

(15b)

式中,Wij、Fmn分别为横向位移w、应力函数Φ的广义坐标，代入动力平衡方程式(12)中有

(16)

代入相容方程式(13)中有

(17)

式中:()′=∂/∂x;()*=∂/∂y。

2 伽辽金离散

取λi=(πi)/L,γj=(πj)/L。将平衡方程式(16)两边同乘wab(x,y)，并在面积上积分

(18)

两边同除(ρhL2)/4，得到平衡方程式为

Ψab(Tkl+Cpq)=Fab

(19)

式中：

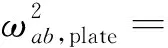
对相容方程式(17)的两边同乘wmn(x,y)，并在面积上积分有

(20)

令Fmn前系数为1，可得

(21)

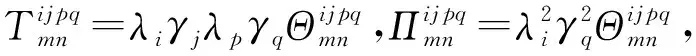
将式(21)代入式(19)，可以得到最后的振动微分方程表达式为

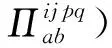
Ψab(Tab+Cab)=Fab

(22)

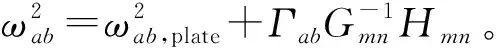
为书写方便，后续将挠度方向的位移wn改写为xn，ζn为系统的阻尼参数，ωn为系统的固有频率之一；Mn为各个平方非线性项前的系数。

3 内共振1∶2∶2时的摄动分析

为了分析主共振，使强迫项的量阶与非线性项和阻尼项一起出现在同一个摄动方程中，引入与振幅有关的、无量纲的小参数ε。代入式(22)得系统的非线性动力学方程

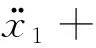
εm4x1x2+εm5x1x3+εm6x2x3+ε(ΔT+ΔC)=

εf1cos(Ωt)

(23a)

εm10x1x2+εm11x1x3+εm12x2x3+ε(ΔT+ΔC)=

εf2cos(Ωt)

(23b)

εm16x1x2+εm17x1x3+εm18x2x3+ε(ΔT+ΔC)=

εf3cos(Ωt)

(23c)

根据ε的任意性，式中ε同次幂的系数必然自行平衡，从而得到如下方程组

ε0阶

(24a)

(24b)

(24c)

ε1阶

ΔC+f2cos(Ωt)

(25b)

ΔT+ΔC+f3cos(Ωt)

(25c)

由于式(24)的解依赖于参数ε，从而将解展开为一次近似解一致展开式

x1(t;ε)=x10(T0,T1)+εx11(T0,T1)

(26a)

x2(t;ε)=x20(T0,T1)+εx21(T0,T1)

(26b)

x3(t;ε)=x30(T0,T1)+εx31(T0,T1)

(26c)

由于式(24)是一个线性常微分方程，因此通解可以表示为

(27a)

(27b)

(27c)

将式(27)代入式(25)中，得

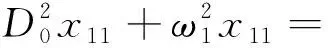
ΔC+cc+NST

(28a)

ΔC+cc+NST

(28b)

ΔC+cc+NST

(28c)

式中:cc为前面项的复共轭项;NST为不产生长期项的所有项。

同时利用有限元软件ABAQUS对图1的模型进行仿真建模和数值分析，对比结果如表2所示。从表2可知，反对称铺设双稳态层合扁壳前6阶固有频率值的理论与数值模拟对比结果的平均误差率仅为0.197%，可知理论解与仿真结果具有良好的一致性，进而验证了理论方法应用在双稳态线性系统上的可行性。

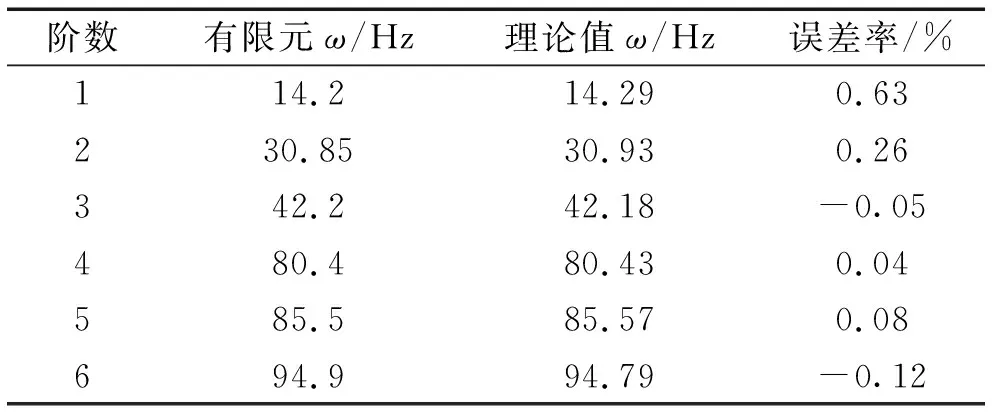
表2 反对称铺设双稳态扁壳固有频率值的理论值与有限元对比Tab.2 Comparison between theoretical value and finite element method of natural frequency value of antisymmetric bistable shallow shell

由线性系统的固有频率可知，双稳态系统中第3～第5阶存在1∶2∶2内共振关系。在主共振Ω接近ω1的前提下，令Ω=ω1+εσ1,ω2=2ω1+εσ2,ω3=2ω1+εσ3,其中σ1、σ2、σ3为调谐参数，将其代入式(28)其可解性条件为

(29a)

(29b)

(29c)

此时引进极进式符号，令An=(aneiθn)/2，并将所得结果分为实部和虚部，得到

(30c)

(30d)

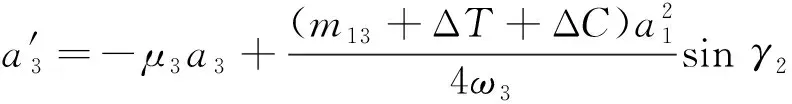
(30e)

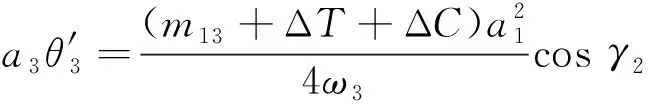
(30f)

式中：

γ1=θ2-2θ1+σ2T1

(31a)

γ2=θ3-2θ1+σ3T1

(31b)

γ3=σ1T1-θ1

(31c)

消去θ1和θ2，得到极坐标下的平均方程

(32a)

(32b)

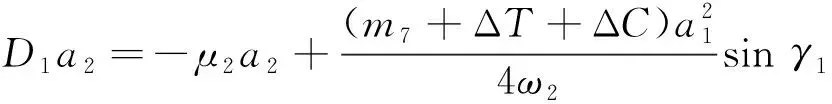
(32c)

(32d)

(32e)

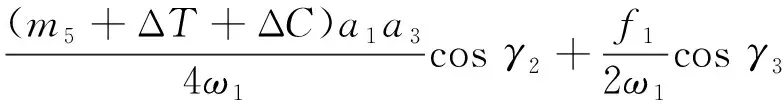
(32f)

令A1=x1+ix2,A2=x3+ix4,A3=x5+ix6。同时代入式(29)的条件中，得到直角坐标的平均方程，形式如下

(33c)

(33d)

(33e)

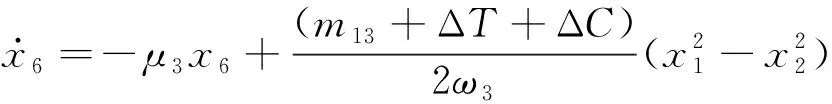
(33f)

4 内共振1∶2∶2时的分叉和混沌动力学分析

通过双稳态系统在温度为30 ℃，湿度为60%RH的条件下，主共振Ω接近于ω1和1∶2∶2内共振结合的情况下的直角坐标平均方程式(33a)～式(33f)，利用数值方法分析双稳态系统随外激励改变而发生的非线性动力学行为特性。

首先给定初始条件为x1=0.1,x2=0.24,x3=0.15,x4=0.26,x5=0.13,x6=0.28,其他参数取值为μ1=0.25,μ2=0.12,μ3=0.2,m4=5.8,m5=3.4,m7=2.5,m13=1.2,ΔT=0.025, ΔC=0.065。在直角坐标平均方程中，f1为与外激励相关的参数，这里选定f1为控制参数来研究系统受到外激励影响的非线性动力学特性。

反对称正交铺设的双稳态系统第1阶和第2阶模态的分叉图，如图2和图3所示。横坐标轴表示的是与外激励有关的f1的变化，纵坐标轴表示的是与系统第1阶和第2阶振幅相关的x1和x3的变化。随着外激励的增大，该系统的分叉图出现明显的上下振动现象，这表明反对称铺设双稳态层合圆柱壳的非线性动力学行为表现出双稳态的基本特征。在f1∈[6.5,7.3]的区间内，双稳态结构一直处于倍周期状态之中。在f1∈[7.3,8.5]的区间内，双稳态结构处于混沌运动当中，振幅不断扩大。

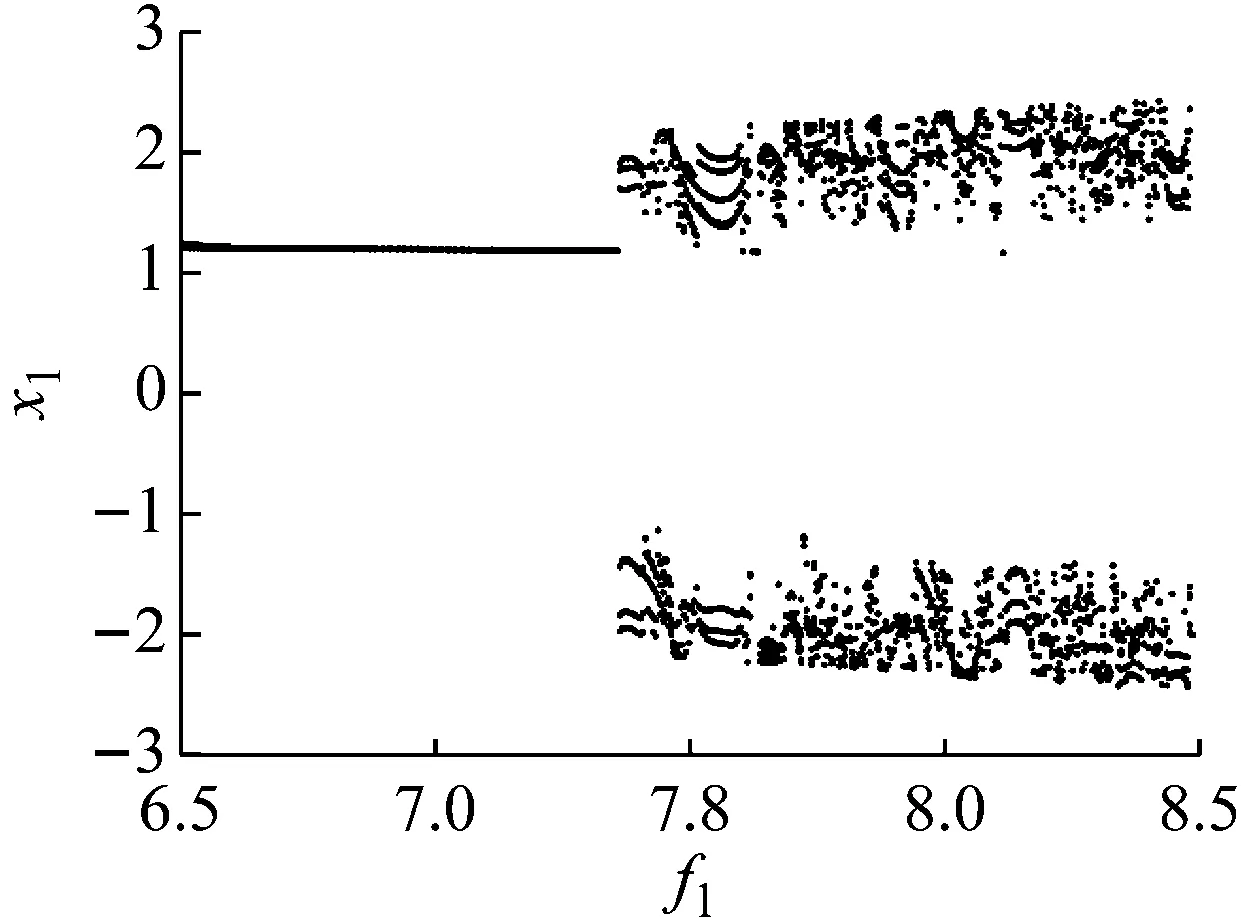
图2 反对称正交铺设双稳态系统第1阶模态的分叉图Fig.2 Bifurcation diagram of first-order modal of cross-ply laying bistable system

图3 反对称正交铺设双稳态系统第2阶模态的分叉图Fig.3 Bifurcation diagram of second-order modal of cross-ply laying bistable system

反对称正交铺设的双稳态系统的最大李雅普诺夫指数图，如图4所示。横坐标轴表示的是与外激励有关的f1的变化，纵坐标轴表示的是最大李雅普诺夫指数。从图4可知，在f1接近6.8左右的区间内，最大李雅普诺夫指数小于零，当在f1的其余区间内，最大李雅普诺夫指数一直大于零，说明双稳态结构一直处于混沌状态之中。下面将选定f1的取值，给出不同外激励值下系统的波形图、相图、庞加莱截面图以及频谱图。

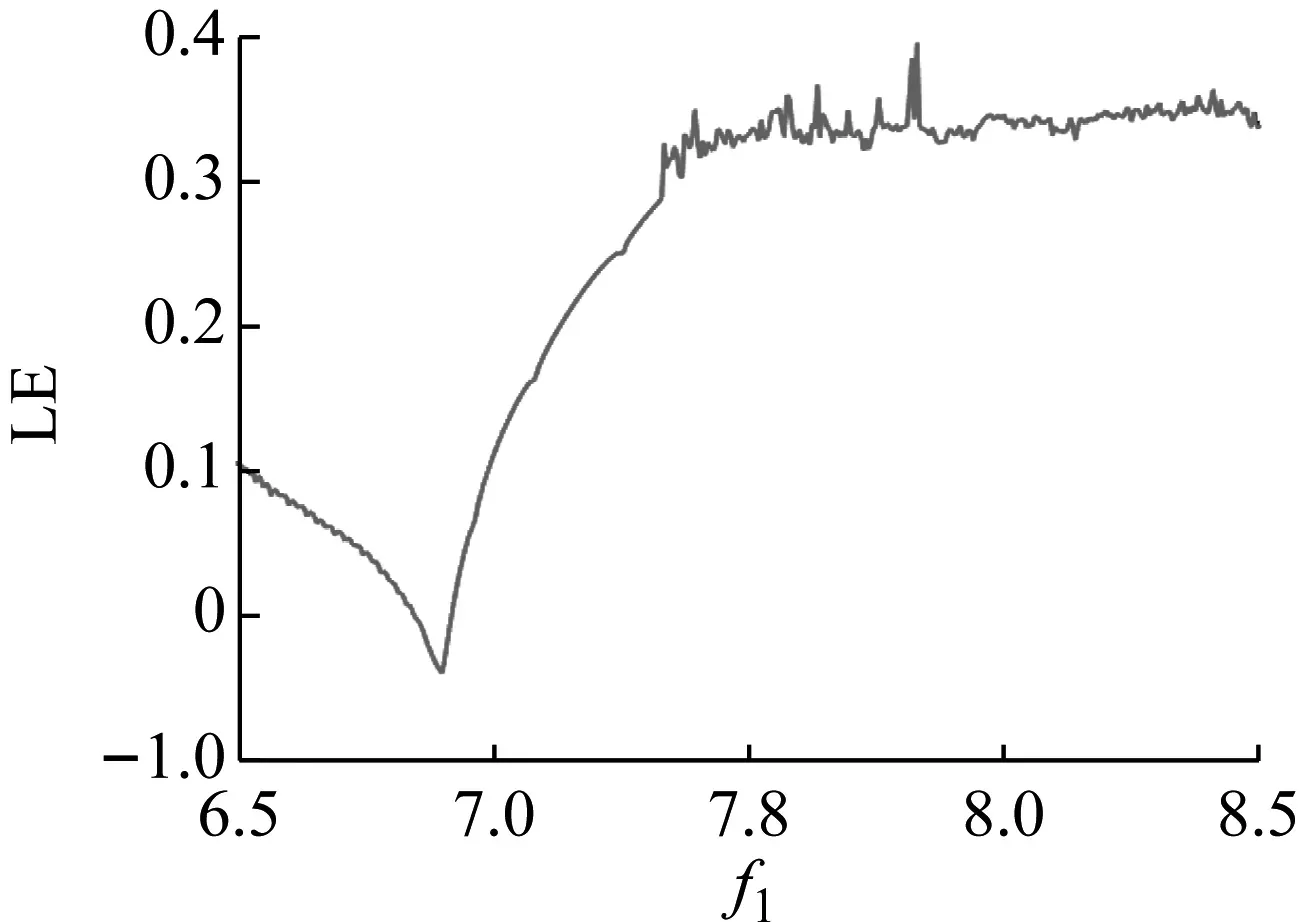
图4 反对称正交铺设双稳态系统最大李雅普诺夫指数图Fig.4 The maximum Lyapunov exponent diagram of cross-ply laying bistable system

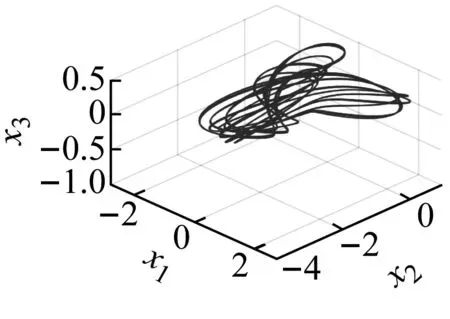
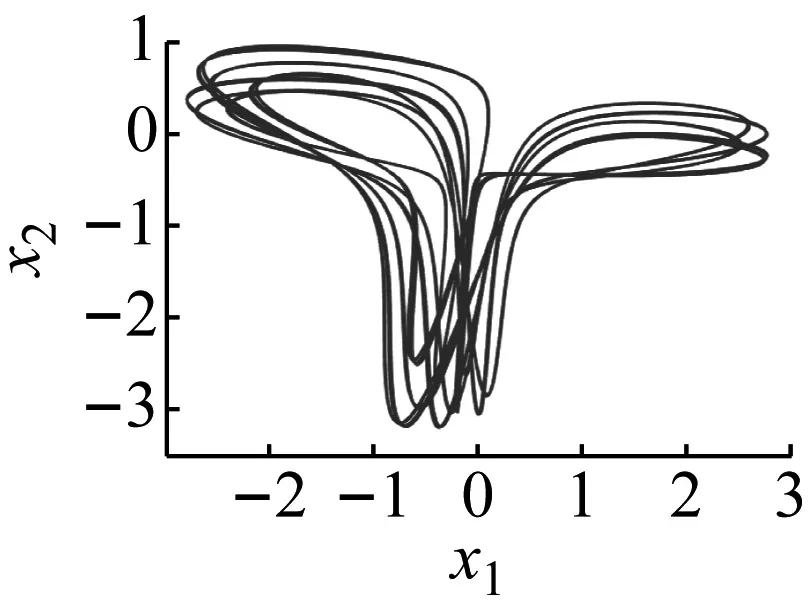
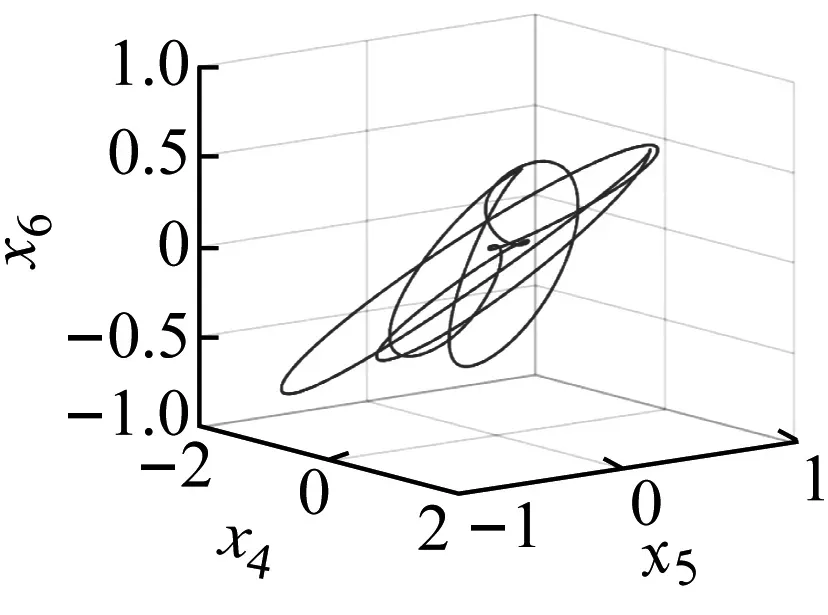
选定不同外激励f1的参数值时对应系统运动的相图、时间历程图、Poincaré截面图和频谱图,如图5～图8所示。在各图中，图(a)和图(b)分别为在空间(x4,x5,x6)上的三维相图和(t,x5)上的时间历程图，图(c)和图(d)分别为空间(x1,x2,x3)上的三维相图和二维平面(x1,x2)的二阶模态相图，图(e)和图(f)分别为在二维平面(x1,x2)上的Poincaré截面和频谱图。

(a)

(b)

(c)

(d)

(e)

(f)图5 f1=7.5时系统的混沌运动Fig.5 Chaotic motion when f1=7.5

(a)

(b)

(c)

(d)

(e)

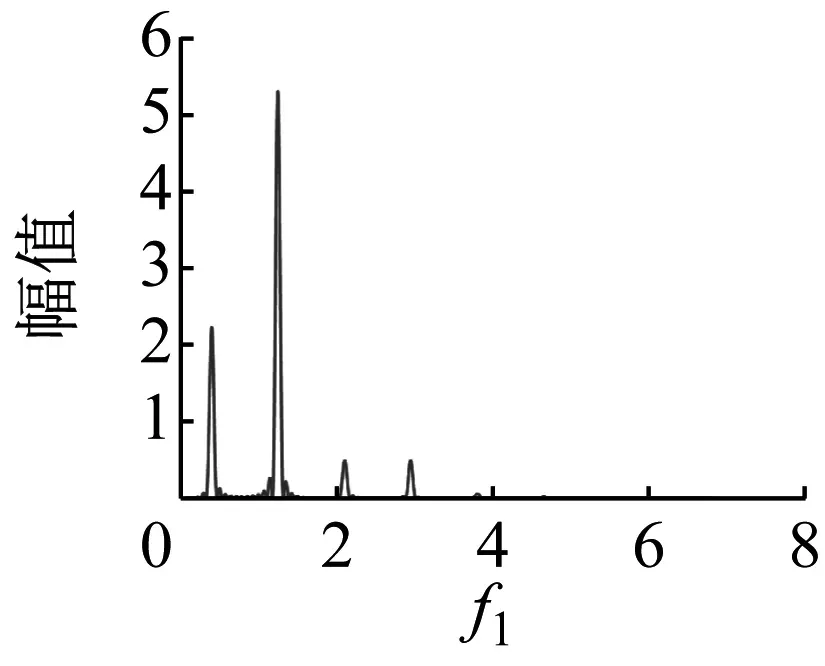
(f)图6 f1=7时系统的周期运动Fig.6 The periodic motion when f1=7

(a)

(b)

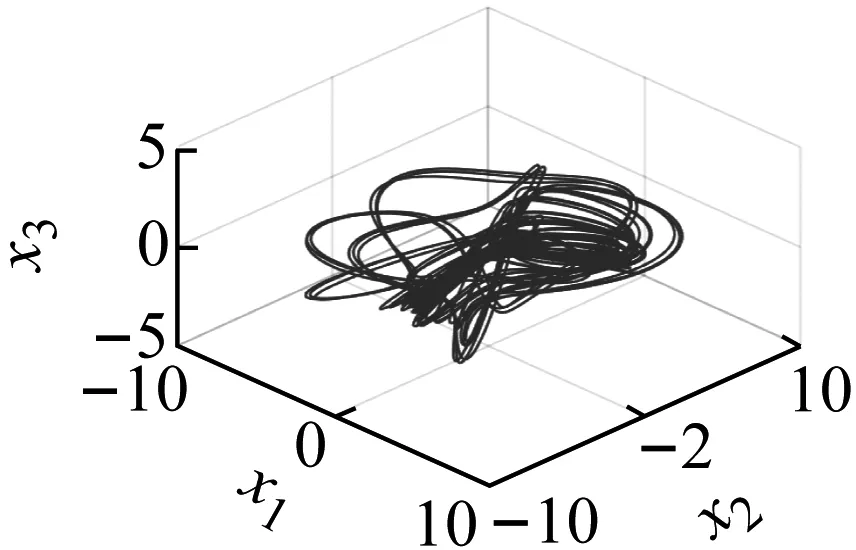
(c)

(d)

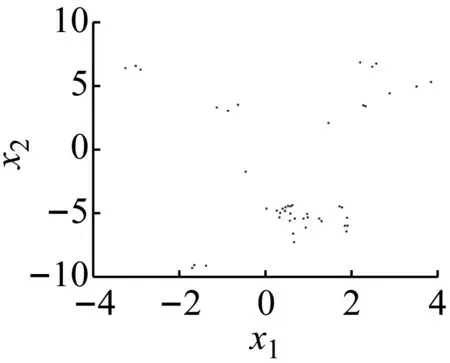
(e)

(f)图7 f1=8时系统的混沌运动Fig.7 Chaotic motion when f1=8

(a)

(b)

(c)

(d)

(e)

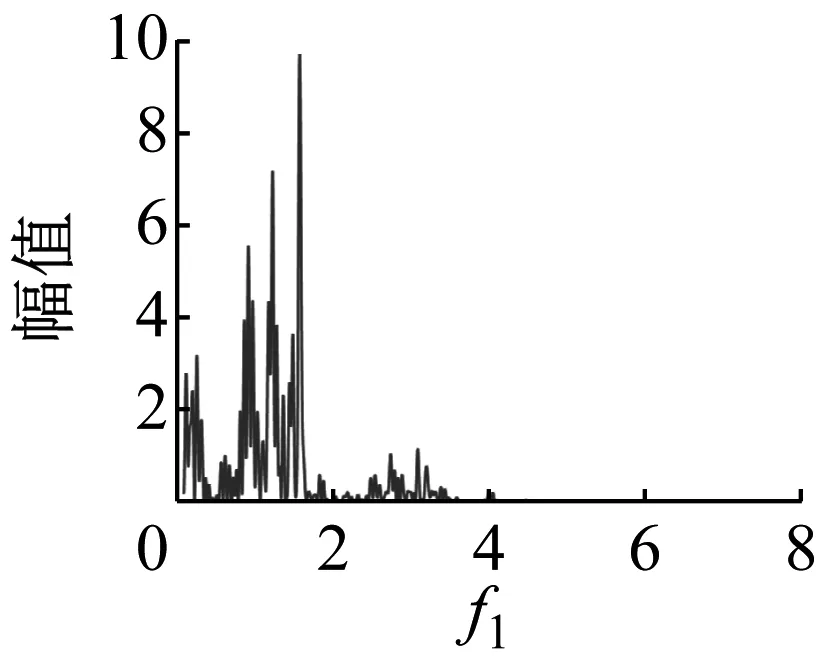
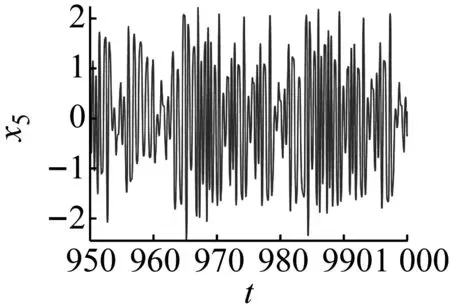
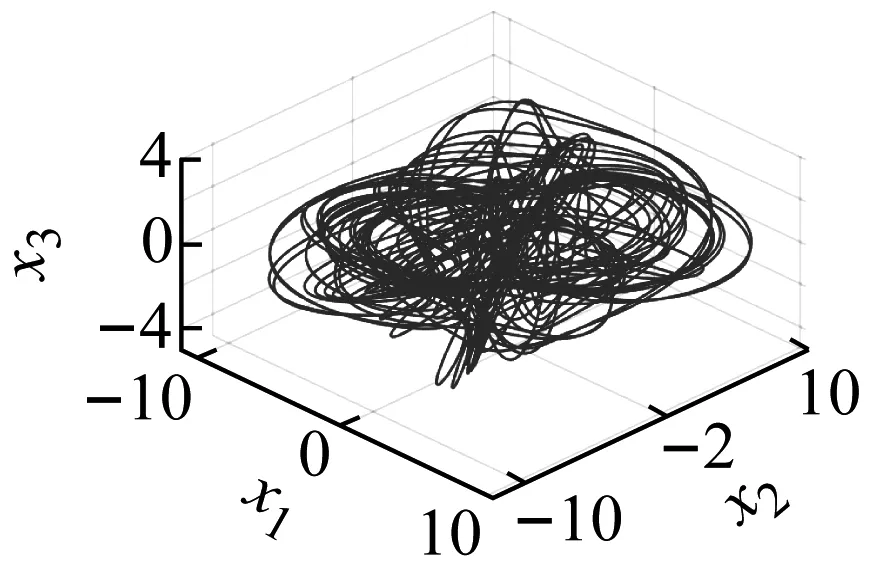
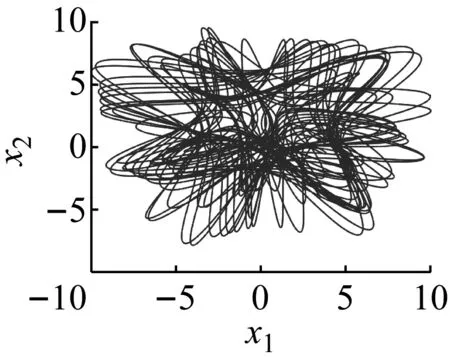
(f)图8 f1=8.5时系统的混沌运Fig.8 Chaotic motion when f1=8.5

当f1=7.5时，由图5可知，系统发生了混沌现象。系统的相图轨迹杂乱密集并且明显有界，频谱图中出现了连续谱，庞加莱映射中出现无数映射点，最大李雅普诺夫指数大于零，这些都说明此时系统中发生了混沌运动。

当f1=7时，由图6可知，系统发生了周期现象。系统的二维、 三维相图中呈现出环状稠密轨道，庞加莱映射中出现密集映射点，频谱图是离散谱，且最大李雅普诺夫指数接近于零。由图6的这些特征可判断，此时系统发生了概周期运动。

当f1=8时系统的运动特性，系统的相图轨迹杂乱密集并且明显有界，频谱图中出现了连续谱，庞加莱映射中出现无数映射点，最大李雅普诺夫指数大于零，这些都说明此时系统中发生了混沌运动(见图7)。

当f1=8.5时系统的运动特性，系统的相图轨迹杂乱密集并且明显有界，波形图表明系统运动具有随机特征，频谱图中出现了连续谱，庞加莱映射中出现无数映射点，最大李雅普诺夫指数大于零，这些都说明此时系统中发生了混沌运动(见图8)。

5 结 论

本文对湿热环境下的反对称正交铺设双稳态壳结构进行了非线性动力学建模和非线性动力学分析。得出以下主要结论：

(1) 在经典壳理论的基础上，考虑温度和湿度的影响，在本构方程中加入热膨胀系数和湿膨胀系数。

(2) 联立相容方程和动力平衡方程以建立模型，得到了反对称正交铺设双稳态壳结构的偏微分运动控制方程。最后应用Galerkin方法对系统偏微分运动控制方程进行三阶离散，得到了三自由度的常微分运动控制方程。

在温度为30 ℃，湿度为60%RH的条件下进行了多尺度分析和摄动分析，得到了1∶2∶2内共振条件下的反对称铺设双稳态结构的非线性动力学响应。由系统分叉图可知，反对称正交铺设双稳态系统存在周期和混沌等典型非线性现象。取一定的参数值，利用相图、时间历程图、频谱、庞加莱映射、最大李雅普诺夫指数分析了系统的具体运动状态，说明激励对双稳态模型的动力学特性有显著影响。