融合改进关联度与Newman算法的区域交通划分研究

王 磊，罗 杰

南京邮电大学 自动化学院、人工智能学院，南京 210046

现代社会，随着经济与城市化的高速发展，路段交通流不断增大，使得城市的交通路网拥堵问题日益严重[1]。现有的交通控制系统越来越难以解决交通拥堵问题，因而对于以优化区域协调控制为目标的子区动态划分方法的研究越来越受到社会的重视。

Walinchus于1971年首次提出交通路网子区，认为路段特征、车流饱和度、相邻交叉口相位差等是子区划分时所应考虑的因素[2]，此后在关于区域路网划分的研究上，多是以交叉口关联度指标为基础，结合各种算法对子区进行动态划分；Hu等根据主干道上交叉口间的实时交通流数据提出路段间的关联度模型[3]；唐秋生等以离散指标、阻滞指标、主路径指标为神经元输入，提出一种基于改进自组织神经网络的路网划分方法[4]；曲大义等考虑了车流离散性、阻滞性和交通流特征规律，提出了一种相邻交叉口关联度，并利用聚类分析动态划分路网中的交叉口群[5]；Dimitriou等对比了K-mean算法与METIS算法的路网划分效果，发现K-mean算法对纯数值对象的聚类性能优于METIS算法[6]；Shen等定量分析了交叉口间距、交通流密度、周期时长对交叉口关联度的影响，提出了一种基于模糊算法的路网划分方法[7]；Tang等采用灰色关联分析和谱聚类的方法对过饱和及其相关区域进行划分，提出了城市过饱和区及其相关区域的交通协调控制模型[8]。

以上研究表明，通过对相邻交叉口关联度进行定量分析，并结合相关算法建立子区划分方法，在一定程度上能够优化区域协调控制。然而大部分关联度模型并未充分考虑区域路网的动态影响因素，多数指标仍是建立在交叉口间距与交通流量的基础上，或是交通监管者依据路口间距或交通流特性对路网进行粗糙的划分，效果总是不尽如人意。因此，对于路网的子区划分关联度指标与划分方法皆有待进一步研究与改进。

本文充分考虑了交叉口间距、路段流量、车队长度、行驶时间、车队离散性、车流密度等，建立了改进关联度模型。基于复杂网络的研究，改进经典Newman算法，并基于改进的关联度，对区域路网进行实时动态划分。仿真实验结果表明，所提出的子区划分方法能够有效提升划分效果，为优化区域交通路网协调控制提供良好的基础。

1 区域交通路网模型

研究表明，在划分区域路网时，各相邻交叉口间距一般不能大于800 m，因为如果交叉口距离过大，如超过1 000 m时，会导致路段上的车流离散性很大，降低了相邻交叉口间的关联度，不利于区域交通的协调控制[9]。本文中所选取的区域路网中的“丁”字路口均采用3相位控制模式，“十”字路口均采用4相位控制模式。区域路网模型如图1所示。

图1 区域路网模型图Fig.1 Regional road network model diagram

2 改进交叉口关联度

相邻交叉口之间的关联特征通常受路段流量、交叉口间距、车速、车流离散性、车辆排队、车流密度等诸多因素影响。显然，相邻交叉口间距属于静态因素，因此其对关联度的影响是固定的，然而当其结合平均车速后，由于车速为实时变化的，因此会变为动态因素；路段流量、车流离散性、车辆排队、车流密度则实时影响交叉口间的关联程度，属于动态因素。而现有的关联度模型对以上因素大多并未考虑周全。

2.1 经典Whitson关联度模型

其主要考虑了交叉口间距，行程时间，路段流量三种因素，是一种常用的交叉口关联度计算方式，见式（1）：

式中，I(i,j)为两相邻交叉口i与j之间的关联度；t为车辆通过两相邻交叉口的行驶时间；n为自上游交叉口驶向下游交叉口的车流分支数，通常对于“丁”字路口而言，n=2，对于“十”字路口而言，n=3；qmax为从上游交叉口i驶入下游交叉口j的最大分支流量；为自上游交叉口驶入下游交叉口的交通量总和为自上游交叉口驶入下游交叉口车流量的不均匀指标。

2.2 引入排队长度的Whitson关联度模型

胡华等认为Whitson关联度模型未考虑下游交叉口车辆排队长度这一关键因素，因而引入排队长度这一变量对模型参数t进行修改[10]，见式（2）：

式中，t为车流自上游交叉口入口至下游交叉口入口排队车辆尾车（当进口有车辆排队时）或进口停车线（当进口无车辆排队时）之间的平均行驶时间；L为两交叉口间的距离；l为下游交叉口入口车道的车辆排队长度；vˉ为车流在两交叉口间的平均速度。

2.3 Whitson关联度模型的进一步改进

由式（1）和式（2）可知，改进的Whitson关联度模型虽然考虑了相邻交叉口之间的车辆排队长度与车流不均匀性，但是却忽略了上游交叉口中不同相位对驶入下游交叉口车流量的影响，即未考虑从上游交叉口驶向下游交叉口的车流在时间上的离散性，此外，该模型也未考虑到如下情况：当驶入上游交叉口的车流m驶向下游交叉口时，其每一股车流都有可能分别驶入左转、直行、右转这三股下游交叉口入口车道，而不同的车流m驶入这三股入口车道的流量也不尽相同，即该模型仅将上游交叉口的流入车流作为整体进行分析，而未考虑自上游交叉口驶入下游交叉口的车流在空间上的离散性。如图2所示。

图2 交叉口信号相位简化图Fig.2 Simplified phase diagram of intersection signal

因此，在综合考虑了以上两种情况后，本文对已改进的Whitson关联度模型进行进一步改进，提出相邻交叉口间的车流离散系数。

定义xi→j为交叉口i在一个周期内允许车流驶入交叉口j的相位；Xi→j为交叉口i中允许车流驶入交叉口j的相位总数；yi→j为从交叉口i到交叉口j的入口车道（包括左转、直行、右转）；Yi→j为从交叉口i到j的入口车道总数；qxi→jm为驶入交叉口i的各车流m在相位xi→j内驶向交叉口j的流量；为各车流m汇入交叉口j的入口车道yi→j的流量；而又由式（1）可知，qm为驶入交叉口i的车流m的流量，因此可求得所有驶入交叉口i的车流m通过相位xi→j汇入下游入口车道yi→j的总流量为：

由式（3）可求出所有车流m在一个周期内通过不同的相位xi→j汇入各个下游入口车道yi→j的最大流量为：

式中，qi→j(max)为所有车流m通过不同的相位xi→j汇入各个下游入口车道yi→j的最大流量。由于考虑了车流在不同相位时间与不同入口车道空间上的离散性，式中xi→j与yi→j都是可变的，而非某一固定值。

再由式（4）可进一步推导出交叉口i到j的车流离散系数为：

最后，将所提出的车流离散系数代入式（1），可得改进后的Whitson关联度模型为：

2.4 车流密度影响系数

相邻交叉口间的车流密度是指在单位长度（通常为1 km）路段同一方向上单位时间内的车辆数[11]，其大小反映了两交叉口间路段的拥挤程度，因此也是判断两相邻交叉口是否需要协调控制的一个重要因素。本文基于车流密度这一概念，提出交叉口i与交叉口j之间的车流密度影响系数：

式中，τ为某一时间段；L为两交叉口i与j之间的距离；qi→j为车流在时间τ内从交叉口i驶向j的总流量；si→j为车流从交叉口i驶向j的饱和流率；ρi→j为从交叉口i驶向j的车流在时间τ内的平均流量密度；ρs(i→j)为从交叉口i驶向j的车流在饱和状态下的流量密度；Fρi→j为车流从交叉口i驶向j的车流密度影响系数。

综上，本文基于前人已改进的Whitson关联度模型，提出相邻交叉口间的车流离散系数，对模型进一步改进，并基于车流密度提出交叉口间的车流密度影响系数，建立相邻交叉口间的离散-密度关联度模型，见式（8）：

式中，I(i→j)为两交叉口i到j的离散-密度关联度；ni→j为车流从交叉口i驶入j的分支数；μi→j为交叉口i到j的车流离散系数；ti→j为车辆自交叉口i入口行驶至交叉口j入口排队车辆尾车的平均行驶时间；Fρi→j为交叉口i到交叉口j的车流密度影响系数。

考虑到相邻交叉口间的路段交通流通常具有双向性，因此，根据式（8）可以求出交叉口j到交叉口i的离散-密度关联度I(j→i)，两交叉口间关联度取I(i→j)与I(j→i)的平均值，因此交叉口i与交叉口j的最终关联度为：

3 改进子区划分方法

根据复杂网络中对社团划分的研究[12]，首先在传统的Newman算法中引入边权，对其模块度进行改进，其次将区域路网抽象为社团网络，路网中的交叉口抽象为节点，相邻交叉口间的路段抽象为边，在改进的Newman快速算法中引入离散-密度关联度，将其作为节点i与节点j之间的边权，提出改进的子区划分方法。

3.1 社团划分算法中的参数介绍

节点度是网络图中最基本的概念之一，节点i的度ki是指在社团网络中与此节点相连的总边数，可简单明了地表现节点的网络特性，是权衡一个节点的重要性的指标之一，ki的值越大，说明节点i在网络中越重要，反之则越不重要；边权wij是连接节点i与节点j之间边的权值，以此来衡量两个节点之间关联性的强弱，wij的值越大，说明节点i与j之间的关联性越强，反之则越弱；点权di是所有与节点i连边的权值之和，即di=，通常用来描述节点在网络中的作用性大小，di的值越大，说明节点i在网络中所占的权重越大，则其在网络中所起的作用越大，反之则越小。

3.2 模块度介绍

模块度[13-14]是一种用来评判社团划分结果优劣的标准，通常用Q来表示，Q值越大，表明划分结果越好。在一个特定的社团划分过程中，当社团模块度Q最大时，划分结果最优，此时模块度为Qmax，其取值范围一般在0.3～0.7之间。

在无权网络中，Q的表达式为：

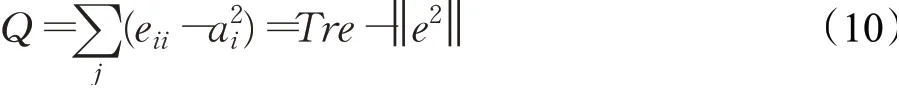
式中，eii为社团i中的边数在整个网络总边数中的占比；Tre为所有社团的内部边数在整个网络总边数中的占比。

3.3 传统Newman算法

Newman算法[13-14]是Newman等基于GN算法所提出的社团凝聚算法，该算法实质上是一种基于贪婪算法思想的凝聚算法，其算法流程如下：

（1）将初始网络分成为n个社团，一个节点表示一个独立社团。定义一个n阶对称矩阵E和一个一维数组A，其中，矩阵E的行列数等于网络的总节点数，其元素eij为社团i与社团j间相连的边数在网络总边数中的占比；数组A的元素个数等于网络的节点总数，其元素ai为社团i的内部节点与外部节点相连的边数在网络总边数中的占比。则初始的eij与ai满足：

式中，p为网络中的总边数；ki为节点i的度。

（2）将相互连接的社团依次合并，然后计算模块度增量ΔQ，由贪婪算法可知，社团应朝着模块度增加速度最快的方向合并，ΔQ的计算公式为：

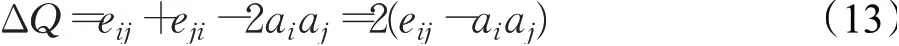
将相应的ΔQ的社团i与j进行合并，并将合并之后的模块度值记录下来。在每次的合并之后，分别更新

（3）将步骤（2）反复执行，持续地合并社团，当整个网络合为一个社团时，停止合并，最多要进行n-1次社团合并。当模块度最大时，此时的划分结果为最优结果。

3.4 改进Newman算法

传统的Newman算法的提出是基于无权网络，为了能够应用于有权网络，现对传统Newman算法进行改进。

首先对无权网络模块度的表达式进行改进，每个社团网络中的节点都代表一个社团，将初始化的n个社团记为(c1,c2,…,cn)，定义矩阵C=[cij]为n阶对称矩阵，其元素cij为社团i与社团j之间相连的边的边权和在整个网络中总边权的占比；矩阵C的各行元素之和为，表示社团i的内部节点与外部节点相连的边的边权之和在整个网络中总边权的占比，由此可得到改进的模块度，即有权网络的模块度为：

式中，cii为社团i中的边权之和在整个网络中总边权的占比；Tre为矩阵C的对角线元素和，表示所有社团的内部边权之和在整个社团网络中总边权的占比表示矩阵C2的所有元素之和。

与传统的Newman算法相比，改进的Newman算法引入了网络节点间的关联特性，节点间的边权大小即表征了节点间的关联度大小，故可将eij与ai改进为：

式中，wij为节点i与节点j之间的边权。

3.5 改进的子区划分方法

区域路网是一种典型的复杂网络，将改进的Newman算法与离散-密度关联度模型相结合，提出基于引入离散-密度关联度的改进Newman算法的子区动态划分方法，此方法的优越之处在于，其结合了改进Newman算法对边权分析的高效性与精确性以及离散-密度关联度对交通数据采集的实时性，能够依据路网交通流的实时特性对不同时段的路网子区进行快速而准确的划分。

在引入离散-密度关联度模型后，可对式（15）与式（16）进行如下改进：

式中，I(i,j)为交叉口i与j之间的离散-密度关联度。

4 仿真实验

依据所提出的模型与算法，选取南京市栖霞区某区域路网，结合百度地图，在网上实时查询该路网的交通数据，以MATLAB为工具对Newman快速算法进行编程，将基于引入离散-密度关联度的改进Newman算法所划分的结果，分别与基于传统Newman算法所划分的结果、基于引入胡华等改进Whitson关联度的改进Newman算法所划分的结果进行仿真对比。

4.1 路网选取与关联度计算

如图3，选取了南京市栖霞区某区域路网，包含了文澜路、仙林大道、仙境路等16个交叉路口以及23条路段。

图3 南京市栖霞区某区域路网Fig.3 Regional road network of Qixia District，Nanjing City

在网上查询到该区域路网在某天14：00—15：00时段的交通流数据，并测得路网中各相邻交叉口间距，结合图4，可求得胡华等改进Whitson关联度与离散-密度关联度，如表1和表2所示。

表1 14：00—15：00胡华等改进Whitson关联度I(i,j)Table 1 Modified Whitson correlation degree I(i,j)by Hu Hua et al at 14：00—15：00

表2 14：00—15：00离散-密度关联度I(i,j)Table 2 Discrete-density correlation degree I(i,j )at 14：00—15：00

图4 区域路网简化图Fig.4 Simplified map of regional road network

4.2 三种划分方法对比

方法1基于传统Newman算法来划分所选取的区域路网，其社团合并过程所对应的模块度点状图、子区划分结果树状图与路网车流密度简化图分别由图5（a）、（b）、（c）所示。

由图5可知，当交叉口合并至14号时，子区个数为3，对应的模块度最大，为0.397 0，此时的子区划分结果最优，分别为：子区一，交叉口1，2，5，6；子区二，交叉口3，4，7，8，9，13；子区三，10，11，12，14，15，16。这种基于无权网络的划分方法仅以交叉口间的邻接矩阵为模型输入，其划分结果是固定不变的，无法随着交通流的变化而改变，因此没有实用性。

图5 方法1仿真图Fig.5 Method 1 simulation diagram

方法2基于引入胡华等改进Whitson关联度的改进Newman算法来划分所选取的区域路网，其模块度点状图、划分结果树状图与路网车流密度简化图分别由图6（a）、（b）、（c）所示。

由图6可知，当交叉口合并至13号时，子区个数为4，对应的模块度最大，为0.438 4，此时子区划分结果最优，分别为：子区一，交叉口1，2，5，6；子区二，3，4；子区三，7，8，9，12，13，16；子区四，10，11，14，15。与方法1相比，这种划分方法虽然考虑了相邻交叉口之间的车辆排队长度与车流不均匀性，但是并未考虑到其他动态因素的影响，因此其划分结果并不准确。

方法3基于引入本文所提出的离散-密度关联度的改进Newman算法来划分所选取的区域路网，其模块度点状图、划分结果树状图与路网车流密度简化图分别由图7（a）、（b）、（c）所示。

图7 方法3仿真图Fig.7 Method 3 simulation diagram

由图7可知，当交叉口合并至12号时，子区个数为5，对应的模块度最大，为0.633 3，此时子区划分结果最优，分别为：子区一，1，2，5，6；子区二，3，4，7；子区三，8，9，12，13；子区四，11，15，16；子区五，10，14。与方法2相比，此方法在考虑相邻交叉口间车辆排队长度的基础上，进一步将车流不均匀指标改进为车流离散系数，并提出车流密度影响系数，综合考虑了车流在时间与空间上的离散性以及车流密度对区域动态划分的影响，使划分结果更为合理。

为了进一步验证方法3的实时性，本文在相同的区域路网查询17：00—18：00时段的交通流数据，利用方法3进行路网划分，并将划分结果与14：00—15：00时段的划分结果进行对比。17：00—18：00的离散-密度关联度如表3所示。

表3 17：00—18：00离散-密度关联度I(i,j)Table 3 Discrete-density correlation degree I(i,j)at 17：00—18：00

其模块度点状图、划分结果树状图与路网车流密度简化图分别由图8（a）、（b）、（c）所示。

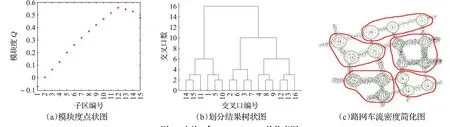
图8 方法3在17：00—18：00的仿真图Fig.8 Method 3 simulation diagram at 17：00—18：00

由图8可知，当交叉口合并至12号时，子区个数为5，对应的模块度最大，为0.557 1，此时子区划分结果最优，分别为：子区一，1，5，10；子区二，2，3，6，7；子区三，4，8，9；子区四，11，14，15；子区五，12，13，16。与14：00—15：00时段的划分结果相比，该时段为晚高峰时期，车流量骤增，其交通流数据也随之变化，其划分结果也随着不同的交通流数据发生了变化，因此可验证方法3具有实时性，能够依据不同时段的交通数据对路网子区进行动态划分。

5 结束语

在已有的关联度模型和复杂网络的研究基础上，以优化区域协调控制为目标，综合考虑了相邻交叉口间距、路段流量、车流速度、车队长度、行程时间、车流离散性、车流密度等因素，提出了一种融合改进关联度模型与改进Newman算法的区域路网动态划分方法。通过仿真实验对比可知，该划分方法有效地结合了不同时间段的实时交通流数据，使得子区划分结果更加合理，对于优化区域交通不合理配时、解决交通拥堵等问题具有重要的价值。