系数增强最小二乘回归子空间聚类法

简彩仁，翁 谦，夏靖波

1.厦门大学 嘉庚学院 信息科学与技术学院，福建 漳州 363105

2.福州大学 数学与计算机科学学院，福州 350108

随着互联网的不断发展，对计算机视觉和模式识别等领域提出了许多研究目标，聚类分析是其中的一个重要分支。子空间聚类是最流行的聚类分析技术之一，在图像表示[1]、运动分割[2]、人脸聚类[3-7]、基因表达数据聚类[8]等领域有着广泛的应用。假设高维数据近似于低维子空间的并集，则子空间聚类旨在寻求一组适合的子空间对给定的数据集进行分割，并基于识别出的子空间进行聚类[5]。

在过去的几十年中，子空间聚类法得到了很好的发展，可以将其大致分为以下四类：迭代方法[9]、统计方法[10]、代数方法[11]和基于谱聚类的方法[1-8，12-13]。近年来，基于谱聚类的方法得到了更多的关注，并在计算机视觉等众多领域中取得了良好的性能[5，6-7，12-13]。这种方法的关键是找到一个块对角亲和力矩阵（affinity matrix），其中亲和力矩阵的元素表示两个对应数据点之间的相似度，而块对角结构意味着类内有非零相似度，而类间的相似度为零。为了获得块对角线亲和力矩阵，一些研究人员提出在谱聚类法中使用自表示策略来测量相似性[3]。具体来说，它们将每个样本点表示为数据集本身中其他样本点的线性组合，然后使用表示系数矩阵构建亲和力矩阵。这些方法之间的主要区别在于求解表示系数矩阵的不同。例如，稀疏子空间聚类（SSC）[3]假设每个样本点都可以由最少的其他样本点线性表示，并最小化表示系数矩阵的L1-范数约束。低秩表示子空间聚类（LRR）[4]确保表示系数矩阵为低秩矩阵，以捕获输入数据的全局结构，LRR对表示系数矩阵最小化核-范数约束。与SSC和LRR不同，最小二乘回归子空间聚类（LSR）[5]采用F-范数约束求解表示系数矩阵，以获得内聚性更强的表示系数矩阵。这些方法在子空间聚类中显示出令人鼓舞的性能。但是由于SSC和LRR需要迭代计算，计算效率低，而LSR具有解析解，因此LSR得到了飞速的发展。近几年，基于LSR的扩展模型层出不穷。核截断回归表示子空间聚类（KTRR）[12]将数据集映射到高维空间，利用最小二乘回归模型求解表示系数，增强KTRR求解的表示系数矩阵刻画数据集非线性的能力。缩放单纯形表示子空间聚类（SSRCS）[13]对最小二乘回归模型的表示系数矩阵加上非负约束和缩放单纯形约束，SSRCS的非负约束有利于聚合来自相同子空间的数据，同时抑制来自不同子空间的数据，缩放单纯形约束将每个系数向量的和限制得到更有区分性的表示系数矩阵[14]。

利用表示理论求解表示系数矩阵，表示系数矩阵元素的大小反映了样本间的相似度，因此样本相似度对求解表示系数矩阵有重要的作用，而最小二乘回归子空间聚类法在求解表示系数矩阵时忽略了样本间的相似度。针对这一不足，利用样本相似度保持的思想定义系数增强项改进LSR，提出一种更加鲁棒的求解表示系数矩阵的方法，从而提出系数增强最小二乘回归子空间聚类法。

1 子空间聚类法概述

基于自表示理论的子空间聚类法的关键在于表示系数矩阵。LSR利用正则F-范数求解表示系数矩阵且具有解析解，得到了许多学者的青睐，因此本章介绍LSR及其扩展方法。

X=[x1,x2,…,xn]∈Rm×n的每一列xi表示具有m个特征的样本，X是有n个样本的数据集。在某种约束条件下，利用X重构X，并求解表示系数矩阵C。LSR[5]利用F-范数的内聚性求解表示系数矩阵：

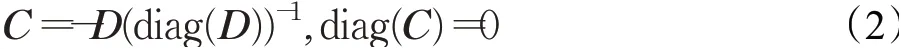
其中，D=(XTX+λI)-1,I是单位矩阵。

KTRR[12]将样本xi和除xi外的样本集Xi=[x1,…,xi-1,xi+1…,xn]∈Rm×(n-1)用非线性映射φ:Rm→H转化为核空间H上的数据φ(xi)和φ(Xi)，并利用最小二乘回归模型求解表示系数：

不难得到ci=(Ki+λI)-1ki,其中Ki=φ(Xi)Tφ(Xi) 是核矩阵，ki=φ(Xi)Tφ(xi)是核向量。根据文献[12]的研究，选用高斯核函数将表示系数合并，并保持主对角线元素全为0，可以得到表示系数矩阵C。

SSRCS[13]对最小二乘回归模型的表示系数矩阵加上非负约束和缩放单纯形约束，得到如下的模型：

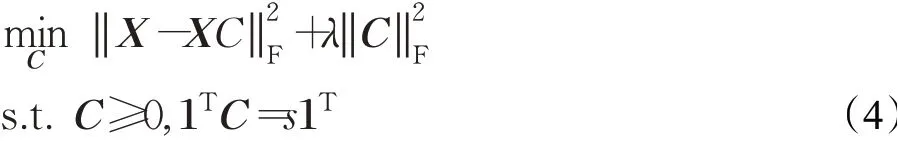
其中，1是所有元素为1的列向量，s是表示系数向量中各项总和的标量，根据文献[13]的研究，取为1。可以利用交替方向乘子法（ADMM）求解该模型，公式（4）可以快速收敛，根据文献[13]的研究，迭代次数取为5。

LSR、KTRR和SSRCS求解得到表示系数矩阵C，定义亲和力矩阵为最后利用标准化分割方法（normalized cuts，Ncut）[12]对A分割实现聚类。

2 CELSR方法

针对最小二乘回归子空间聚类法在求解表示系数时忽略了样本相似度的不足，利用系数增强手段定义系数增强项改进LSR，提出系数增强最小二乘回归子空间聚类法（CELSR）。

2.1 系数增强最小二乘回归模型

假设D=(Dij)n×n是相似度矩阵，其元素Dij刻画样本xi和xj的相似度，一种理想的相似度矩阵是分块对角矩阵，来自相同类的样本的相似度很大，而来自不同类的样本相似度为0。对表示系数矩阵C=(Cij)n×n而言，越大的|Cij|表示样本xi和xj的相似度越高。因此表示系数矩阵跟相似度矩阵有很大的关系，当xi和xj为来自相同的类别时，Dij和|Cij|都很大，当xi和xj为来自不同的类别时，Dij=|Cij|=0。基于这一发现，希望求解的表示系数矩阵能刻画样本间的相似度，因此C和D越接近越好。定义系数增强项为：

考虑到现实数据往往有非线性、多噪声等特点，相似度矩阵D很难达到理想状态，因此需要调节表示系数矩阵C和相似度矩阵D的大小，为此加入平衡参数β＞0。

将公式（1）和公式（5）合并得到系数增强最小二乘回归模型：

其中，γ≥0是正则参数，当γ=0时退化为LSR。第一项是重构损失项；第二项是F-范数惩罚项，使求得的表示系数矩阵有更好的聚合性，保持LSR的优点；第三项是系数增强项，使求得的表示系数矩阵能更好地刻画样本间的相似度。

2.2 模型求解

公式（5）的一种简单直观的解法是，将X=[x1,x2,…,xn]∈Rm×n按一个一个的样本求解表示系数。最后拼接成主对角线元素全为0的表示系数矩阵C=(Cij)n×n。显然这种方法需要求解n次的逆矩阵，计算时间复杂度为O(n4+mn2)。

针对这一不足，给出一种计算效率更高的求解公式（5）的方法。重写公式（5）为：

其中，ei是示性列向量，它的第i个元素为1，其余元素为0，di是D的第i列，约束条件eTi ci=0使得ci的第i个元素为0，这样求得的ci可以满足diag(C)=0。利用矩阵的迹tr和拉格朗日乘数法将公式（7）写为：

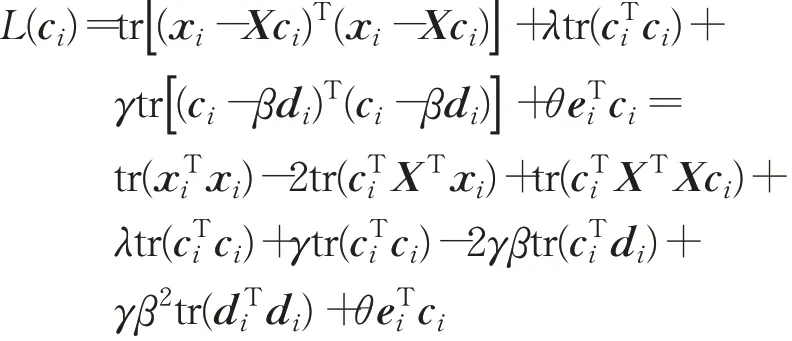
关于ci求导得：

其中，qi=P(XTxi+βdi)，P=(XTX+λI+γI)-1。将表示系数ci拼接成表示系数矩阵C*=[c1,c2,…,cn]。

注意到上面的求解过程只涉及到一次矩阵求逆，因此计算时间复杂度可以降低为O(n3+mn2)。

2.3 系数增强最小二乘回归子空间聚类法

对表示系数矩阵C=(Cij)n×n而言，越大的|Cij|表示样本xi和xj的相似度越高。考虑到表示系数矩阵C和亲和力矩阵A的主对角线元素全为0，将相似度矩阵D也取为主对角线元素全为0的矩阵。因此为操作简便，基于2.1节的分析，本文直接利用公式（1）求解表示系数矩阵C=(Cij)n×n,定义相似度矩阵用于刻画数据集X的全局相似结构。

利用2.2节给出的方法可以快速求到CELSR的表示系数矩阵C*，从而亲和力矩阵为，利用Ncut方法对A进行分割完成聚类。

综上所述，将系数增强最小二乘回归子空间聚类法（coefficient enhanced least square regression subspace clustering method，CELSR）归纳如下：

输入：样本数据X,正则参数λ,γ,β,类别数K。

输出：K个类簇。

步骤1由公式（1）得到表示系数矩阵C=(Cij)n×n，并得到相似度矩阵

步骤2由公式（10）得到表示系数ci，并构造表示系数矩阵C*=[c1,c2,…,cn]；

步骤3由C*得亲和力矩阵，应用Ncut方法将X聚成K个类簇。

3 实验分析

本章通过实验验证CELSR的有效性，包括对比实验、参数讨论和运行效率方面的分析。

3.1 实验方法与实验数据

对比方法为传统聚类法KMEANS，基于最小二乘回归模型的子空间聚类法及其扩展方法LSR、KTRR、SSRSC。为了便于讨论各种方法的聚类效果，将正则参数λ统一取为0.01。其他方法的关键参数设置如下，KTRR的核函数采用高斯核函数，SSRSC的参数s取为1，CELSR的参数γ取为0.1，β取为1.2。

实验数据为常用的标准数据集（https：//jundongl.github.io/scikit-feature/datasets.html），它们分别是4个基因表达数据集Carcinom、lung、lymphoma和nci9，4个图像数据集ORL、orlraws10P、warpAR10P和Yale。它们的简要信息如表1所示。

表1 数据集描述Table 1 Summary of datasets

为了更加全面地比较各种方法的聚类性能，选取聚类准确率（ACC）[14]和标准化互信息（NMI）[14]两个指标比较各种方法的聚类结果。

3.2 对比实验

由于子空间聚类法最后都采用Ncut实现聚类，为了避免随机性，所有方法都运行100次。表2给出了各种方法的聚类准确率平均值±标准差，表3给出了各种方法的标准化互信息平均值±标准差。

从表2和表3的对比实验结果发现，在Carcinom上，CELSR的聚类准确率低于SSRSC，但标准化互信息高于SSRSC。因此在Carcinom上，CELSR和SSRSC的聚类性能差异不大。在Yale上，CELSR的标准化互信息低于KTRR，但聚类准确率高于KTRR。因此在Yale上，CELSR和KTRR的聚类性能差异不大。除此之外，CELSR在聚类准确率和标准化互信息都是最好的。与KMEANS对比，CELSR在聚类准确率和标准化互信息两个指标上的优势更加明显，这一结果说明，CELSR比传统的基于欧氏距离的聚类法更适合高维数据的聚类。与LSR对比，CELSR在聚类准确率和标准化互信息两个指标上有明显的提高，这一结果说明，系数增强项可以求解更加有效的表示系数矩阵，因此考虑保持样本相似度的思想确实可以改进LSR的聚类性能。

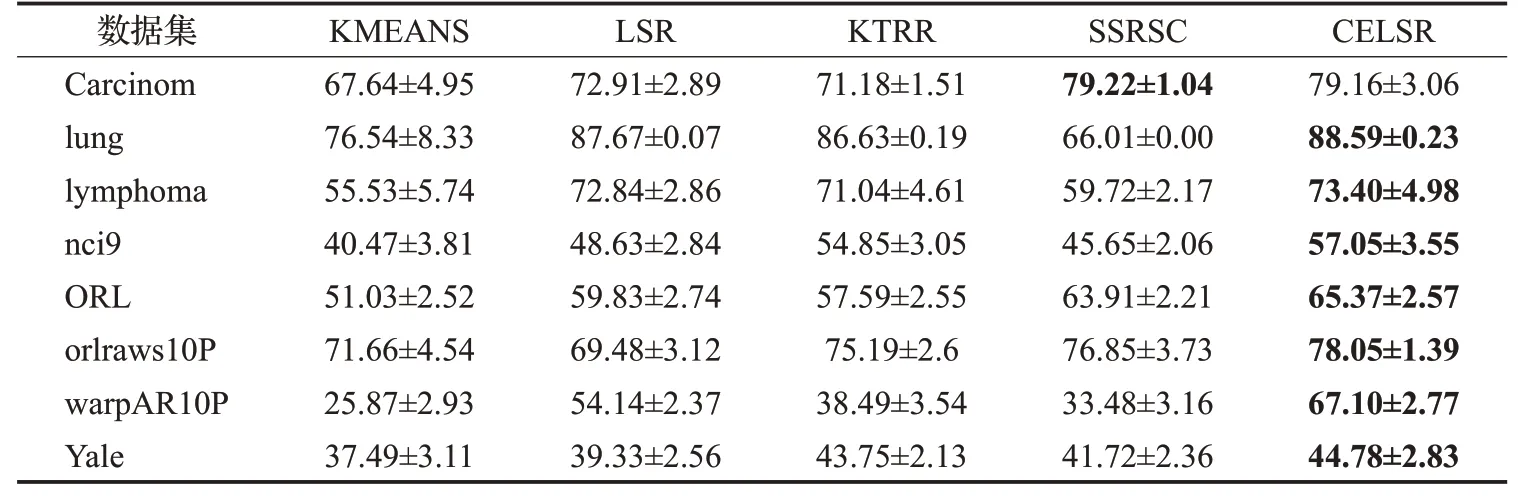
表2 聚类准确率对比Table 2 Clustering accuracy comparison 单位：%

表3 标准化互信息对比Table 3 Normalized mutual information comparison 单位：%

3.3 参数讨论

CELSR有3个参数λ、γ和β，由于不同参数下，聚类准确率的平均值和标准化互信息的平均值的变化趋势差异不大。本节仅讨论参数对聚类准确率的影响，实验结果如图1所示。每个数据有4个子图，依次为β取0.4,0.8,1.2,1.6时，参数λ取0.001,0.01,0.1,1,10,100,γ取0.01,0.1,1,10，CELSR运行100次的平均聚类准确率。从图1的实验结果不难发现，随着参数的变化CELSR的聚类准确率发生明显的变化。当β发生改变时，CELSR的聚类准确率变化不大。除nci9数据集外，较大的λ和γ往往会降低CELSR的聚类准确率。因此在选择λ和γ时，不宜过大。实验结果表明，当λ较小时，CELSR的聚类准确率较为理想，这一结果与LSR的研究结论是一致的。一般的，当λ和γ较小时，γ＞λ的情形下，CELSR的聚类准确率较高，这说明系数增强项能获得更好的表示系数矩阵。

图1 不同λ、γ和β下CELSR在8个数据集上的聚类准确率Fig.1 Clustering accuracy of CELSR on 8 datasets with different λ,γ and β

3.4 运行效率

本节从运行效率的角度比较各种方法的性能，由于LSR、KTRR、SSRSC和CELSR同属于最小二乘回归子空间聚类法的扩展模型，故仅比较4种方法的运行时间。不失公平性，比较各种方法求解表示系数矩阵C的运行时间，各种方法运行500次取平均值，结果如表4所示。

表4的实验结果表明LSR的效率最高，因为LSR具有并行解析解。KTRR、SSRSC、CELSR从不同的角度改进LSR。从表4的结果不难发现，CELSR的运行效率优于KTRR和SSRSC，主要原因是KTRR涉及求解核矩阵，而SSRSC需要迭代求解。这一结果也说明本文给出的CELSR的求解方法具有较高的运行效率。表4的实验结果表明LSR的效率最高，因为LSR具有并行解析解。KTRR、SSRSC、CELSR从不同的角度改进LSR。从表4的结果不难发现，CELSR的运行效率优于KTRR和SSRSC，主要原因是KTRR涉及求解核矩阵，而SSRSC需要迭代求解。这一结果也说明本文给出的CELSR的求解方法具有较高的运行效率。

表4 运行时间对比Table 4 Running time comparison 单位：s

4 结语

本文利用样本相似度保持的思想定义系数增强项，提出系数增强最小二乘回归子空间聚类法（CELSR）。该方法通过系数增强对最小二乘回归子空间聚类法（LSR）进行改进。在常用的8个数据集上的实验结果表明，CELSR可以明显提高LSR的聚类性能。CELSR的聚类结果受参数的影响，如何利用仿生人工智能方法，如蚁群算法等搜索参数，将在以后的研究中给出。