基于随机森林的高速公路运营隧道风险判别法则研究*

2022-10-17乔建刚岳凌峰

中国安全生产科学技术 2022年9期

乔建刚，王傑，岳凌峰

(1.河北工业大学土木与交通学院，天津 300401；2.中交建冀交高速公路投资发展有限公司，河北石家庄 050000)

0 引言

随着国家现代化进程加快，山区高速公路长大隧道群占比逐渐增大。隧道出入口段特殊行车环境，对驾驶员驾驶行为和车辆运行产生一定负面影响，引发交通事故[1]。因此，合理利用已有事故数据，预测隧道不同区段风险程度，探究不同影响因素与事故等级之间的因果关系，对于交通事故预防具有重要意义。

目前，学者运用不同方法对隧道行车安全影响因素及事故严重程度进行研究：赵晓华等[2]基于驾驶模拟，分析长大隧道内驾驶行为与事故风险关系;杜志刚等[3]分析高速公路隧道光环境对交通事故影响；Zhang等[4]从路面纹理方面分析路面性能对隧道行车安全的影响；李倩等[5]通过建立公路隧道交通安全事故树，量化交通事故影响因素重要度；Jian等[6]对新加坡高速公路隧道事故数据进行统计，发现隧道口过渡段事故较严重；Zhang等[7]应用不同类型Logit模型，估计隧道追尾事故风险水平；Caliendo等[8]基于226起高速隧道事故数据，利用随机参数模型分析隧道碰撞事故发生频率影响因素；孙轶轩等[9]构建C5.0决策树，提出影响严重程度的实证规则集。现有研究为隧道不同区段运营风险分析及预测奠定基础，但针对不同风险因素组合对风险等级的影响鲜有研究，对运营风险判别规则的研究也相对较少。

因此，本文以山区高速公路隧道事故数据为基础，应用随机森林模型预测隧道不同路段风险等级，并对风险等级影响因素及决策规则进行分析，研究结果可为隧道行车安全提供决策建议。

1 数据基础及统计分析

1.1 数据来源

收集全国范围内2010—2021年山区高速公路隧道段人员伤亡交通事故共130起，造成366人死亡，656人受伤，数据涵盖全国各个地理分区[10-13]。事故发生地区事故数量占比情况如图1所示。

图1 事故发生地区事故数量占比情况Fig.1 Number of accidents in different geographical divisions as a percentage

结合百度地图开放平台、国家气象信息中心等平台采集事故时空信息，包括事故路段线形、天气数据等。事故等级与公安部[14]一致，严重程度分为特大、重大、一般事故，等级分布如图2所示，重大、特大事故总占比85%，说明山区高速公路运营隧道发生伤亡事故时，人员死亡几率较大。

图2 隧道事故严重程度等级分布Fig.2 Distribution of tunnel accident severity level

1.2 事故严重程度时空分布特征

1) 时间分布

选取当量死亡人数[14]，分析不同隧道区段事故严重程度，将事故伤亡按月份进行统计，如图3所示。

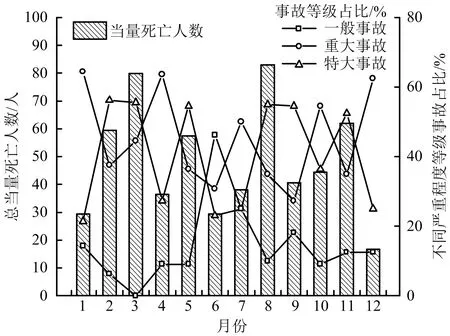
图3 隧道事故严重程度月份分布Fig.3 Monthly distribution of tunnel accident severity

由图3可知，人员伤亡数量较高的月份依次为8，3月，原因在于8月降雨较多，事故数量增加，导致人员伤亡上升。从事故等级占比来看，2，3月份特大事故占比相对最高，大于55%，这是由于2，3月份正值冬季，山区空气湿度较大，低温导致路面湿滑，加上团雾多发，路面、天气双重影响下易引发特大事故。同样，1，4月重大事故占比处于较高水平。

隧道出入口与内部行车环境变化同样影响事故发生，统计1 d中隧道不同位置各时段事故死亡人数，如图4所示。由图4可知，总死亡人数最高的时间段依次是13，19，7～8时，且13时中隧道入口、出口当量死亡人数相对最多，占总量的81.21%，这是由于驾驶员中午易行车疲劳，疲劳驾驶和分心驾驶的概率增大；7，19时中部隧道伤亡较严重，原因是隧道内部行车环境单一，驾驶员疲劳感增加，事故发生概率增加；8，18时出入口处死亡人数较高，这是由于清晨和黄昏时段，环境照度变化剧烈，当洞口处交通设施不合理时，如照明设施损坏，将导致驾驶员心理紧张，易引发交通事故。

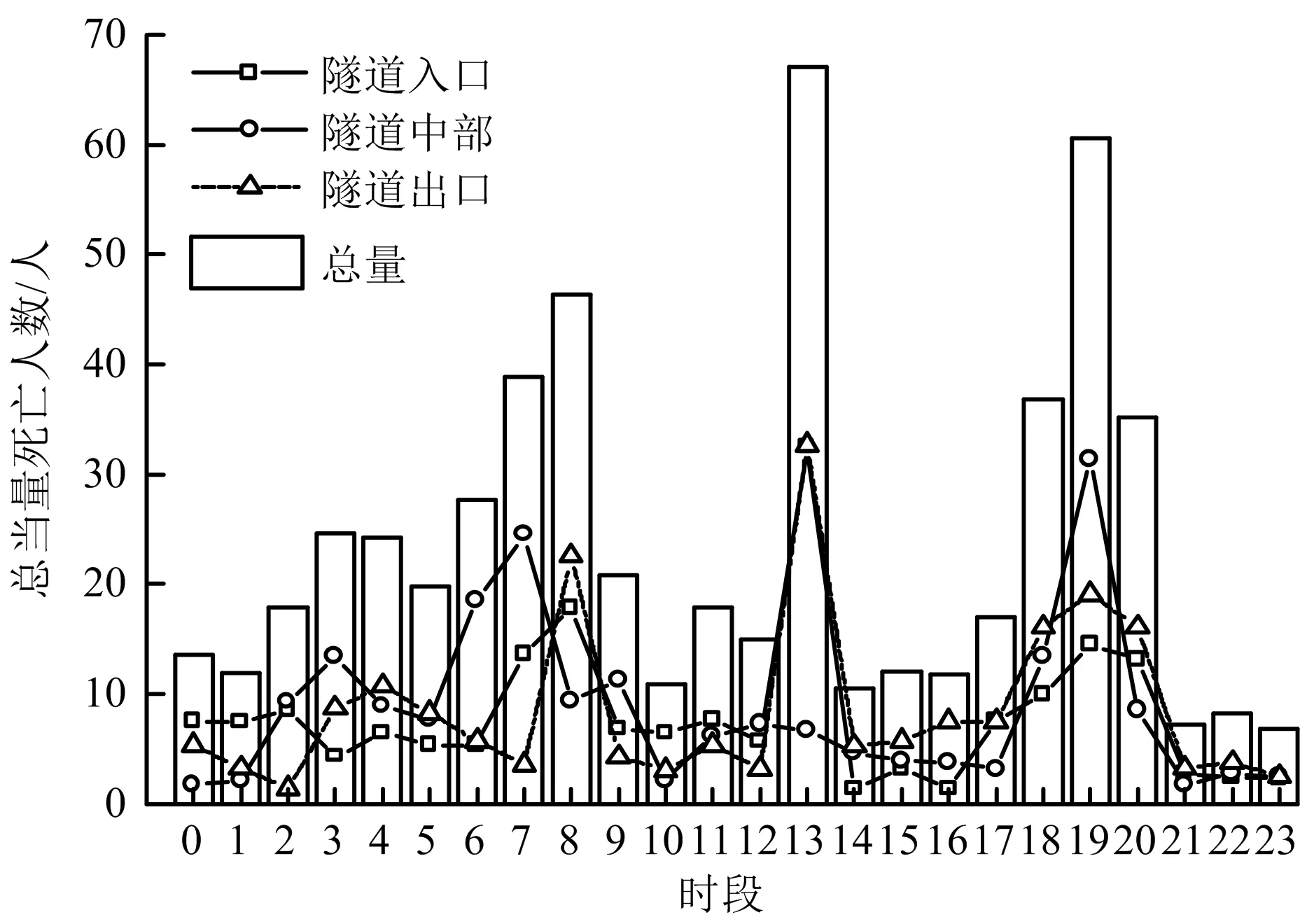
图4 隧道事故严重程度时段分布情况Fig.4 Hourly distribution of tunnel accident severity

2)空间分布

由上文可知，事故人员伤亡与隧道位置有一定关系，但隧道不同区段界定范围没有明确规定[15]。为分析不同区段事故发生情况，综合考虑驾驶员视觉明暗效应[16]、停车视距[17]和路面材料变化[18]划分隧道区段。长度大于500 m的隧道划分如图5所示，小于等于500 m的隧道则不存在区段3。

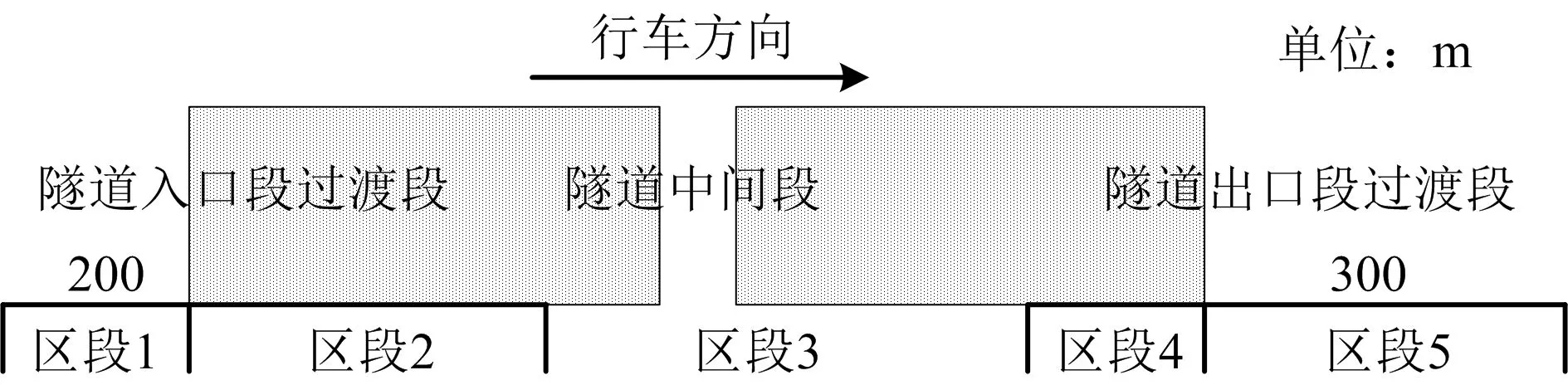
图5 隧道区段划分Fig.5 Tunnel sections division

统计不同区段人员伤亡情况，如图6所示。从死亡人数来看，区段2>区段1>区段4>区段3>区段5，说明隧道入口段事故发生概率较大。这是由于进入隧道时，易产生“黑洞效应”，不利于驾驶员及时发现隧道内部状况，当限速较高时，紧急制动使车辆故障率增大。从事故占比来看，区段1的特大事故占比相对最高，其次是区段5，2个区段均位于隧道与外部环境交接处，易发生交通事故。

图6 不同隧道区段事故伤亡情况Fig.6 Accident casualties in different tunnel sections

1.3 事故严重程度影响因素分析

隧道交通事故严重程度受驾驶员、环境、路面状况、车辆类型等多方面因素影响，因此将事故致因综合为人、车、道路及环境4大因素，事故致因导致人员伤亡占比如图7所示。由图7可知，人的因素导致人员伤亡最为严重，占40.87%，其次为道路因素，为32.17%。

图7 事故原因导致人员伤亡情况占比Fig.7 Proportions of casualties caused by accident causes

1.4 数据处理

综合考虑“人-车-道路-环境”相互作用，从4个方面选取16个影响因素作为自变量，如表1所示。因变量为风险等级，发生特大事故区段风险等级高，为1；发生一般、重大事故区段则为0。

表1 自变量分类Table 1 Classification of independent variables

2 模型理论

决策规则指分类模型中,对样本数据分组时过滤数据的条件，而决策树分类模型中，树根节点到叶节点的路径即为1条规则。随机森林算法(Random Forest,RF)作为多颗决策树的集成，具有精度高、抗噪能力高等优点，规则提取同样可行。

2.1 随机森林模型理论

Breiman于2001年结合Bootstrap重采样和决策树提出RF，从K个自变量中抽取mtry个分支变量，构建ntree棵决策树，根据各决策树分类结果投票，得到预测结果[19]，投票过程如式(1)所示：

(1)

式中：X为决策树中特征自变量；Y为决策结果的类标；R(X)为票数最多的Y；ntree为决策树个数；rit(X)为i决策树中节点t的决策路径函数，i∈[1,ntree]，t∈[1,Ti]，Ti为决策树i中的节点数量。

2.2 决策规则

提取RF中各决策树的叶节点路径，获得决策规则rit(X)[20]，组合形成决策集R，如式(2)～(3)所示：

R={rit|i=1,…,ntree；t=1,…,Ti}

(2)

(3)

式中：Ojc为第i个决策树第t个节点上自变量Xj的取值范围。

根据Nguyen[21]规则，rit(X)规则结构如式(4)所示：

(4)

2.3 规则重要性

RF中重要自变量是指重要性评分VIM(X)排名前40%的自变量，X的重要性评分越高，对Y的影响程度越大，如式(5)所示：

(5)

式中：VIM(Xk)为第k个自变量的重要性评分；Ei为袋外数据计算第i颗决策树的校验误差；Eik为袋外数据随机置换第k个自变量后，第i颗决策树的校验误差。

RF中决策树较多，提取规则数量大，且部分规则缺乏解释性，因此，本文提出规则重要性精炼规则，即通过每条规则所包含规则判断准确率Q1和重要自变量占比Q2，对规则集进行筛选，如式(6)～(7)所示：

(6)

(7)

式中：TPrit(X)，FPrit(X)分别为规则rit(x)判断正确数和判断错误数；Xk′为重要性评分排名前40%的自变量；Count[Xk′,rit(X)]为规则rit(x)中重要自变量出现的个数。Q1越高，规则预测精度越高，Q2越大，规则重要程度越高，规则代表性强。

2.4 预测性能评价指标

评价指标选择分类结果准确率(Accuracy，ACC)、查全率(TP Rate，TPR)和查准率(Precision，PRE)，查全率和查准率2者可对正例样本多的规则结合分类情况进行更全面的评价。

2.5 关键规则集提取流程

在保证原始分类性能前提下，为降低规则数量，提高规则集的可解释性，进一步形成风险判别法则，关键规则集提取流程包括以下5个步骤：

步骤1：提取RF模型中所有决策树规则，保留结果为正例的规则，构建初始决策规则集SETorig。

步骤2：计算初始规则集SETorig中各规则的Q1，Q2，规则重要性评分为Q=Q1+Q2，并排序。

步骤3：依次抽取SETorig中重要性排名靠前的规则，构建简化规则集SETsimp。

步骤4：计算SETsimp在测试集上的分类性能，以ACC作为其评价指标。

步骤5：重复步骤3～4，直至SETsimp连续几次迭代中，ACC未提升或达到迭代次数，得到关键规则集SETcrux，形成判别法则。

3 模型应用

3.1 模型构建

计算所有自变量与严重等级的Pearson相关系数，剔除“隧道长度”和“事故类型”2个变量，其他14个因素作输入自变量。借助Python构建随机机森林回归模型，对mtry和ntree2个参数进行设定，2个参数将影响模型泛化误差和运行时间。考虑影响因素有4类，决策树分支变量应大于4，因此mtry取4，5，6，10，20，50，100，ntree取值为1～50。比较不同参数方案的误差变化，如图8所示，当mtry为5、ntree为45时，模型均方误差较小，模型精度ACC为0.81，分类性能较好。

图8 不同参数下模型误差变化Fig.8 Variation of model error under different parameters

3.2 模型规则提取

对于训练好的RF模型，为计算各规则的规则重要性以及各影响因素重要性评分，得到自变量重要性评分排名如图9所示。评分排名前40%的自变量其重要评分由大到小为涉及车辆数、隧道坡度、驾驶行为、交安设施状况、隧道区段、路面状况。

图9 自变量重要性评分排名Fig.9 Ranking on importance scores of independent variables

利用Python中Matplotlib工具包,可视化RF中45颗决策树，其中原始RF中某颗决策树可视化结果如图10所示。

图10 原始RF中某颗决策树可视化结果Fig.10 Visualization results of a decision tree in original RF

保留决策结果为正例的规则，共369条，分别计算各规则的重要性。根据提取流程,构建关键规则集，并考虑规则的可解释性，样本覆盖数需大于10，最终得到10条规则构成的运营隧道风险判别法则。

3.3 预测性能对比

采用提取到的风险判别法则对测试集数据进行测试，预测分类性能，并与真实值和已训练好的原始RF模型进行对比，预测结果如图11～12所示。

图11 与真实值对比Fig.11 Comparison results with real values

图12 与原始RF模型对比Fig.12 Comparison results with original RF model

由图11～12可知，风险判别法则集预测中有3个事故等级与真实值不同，即发生事故103，104，126的事故风险判为高风险，这与原始RF模型预测结果一致。经分析，3起事故地点均为“隧道入口/出口段+曲线段/弯坡路段”的组合，均发生不安全驾驶行为，虽然已发生事故人员伤亡较低，但该区段仍存在高事故风险，说明风险法则能够发现隧道区段上隐藏的事故风险并进行预测。

与原RF模型预测精度进行对比如图13所示，查全率出现小幅度下滑，查准率基本一致，说明风险判别法则能够较好保留原RF模型的预测能力。此外，判别法则中规则个数相较于原RF模型减少36.9倍，原RF模型与风险判别法则在测试集上运行时间分别为0.419 6，0.100 0 s，说明关键规则集提取方法降低了规则的复杂性以及模型运算时长。

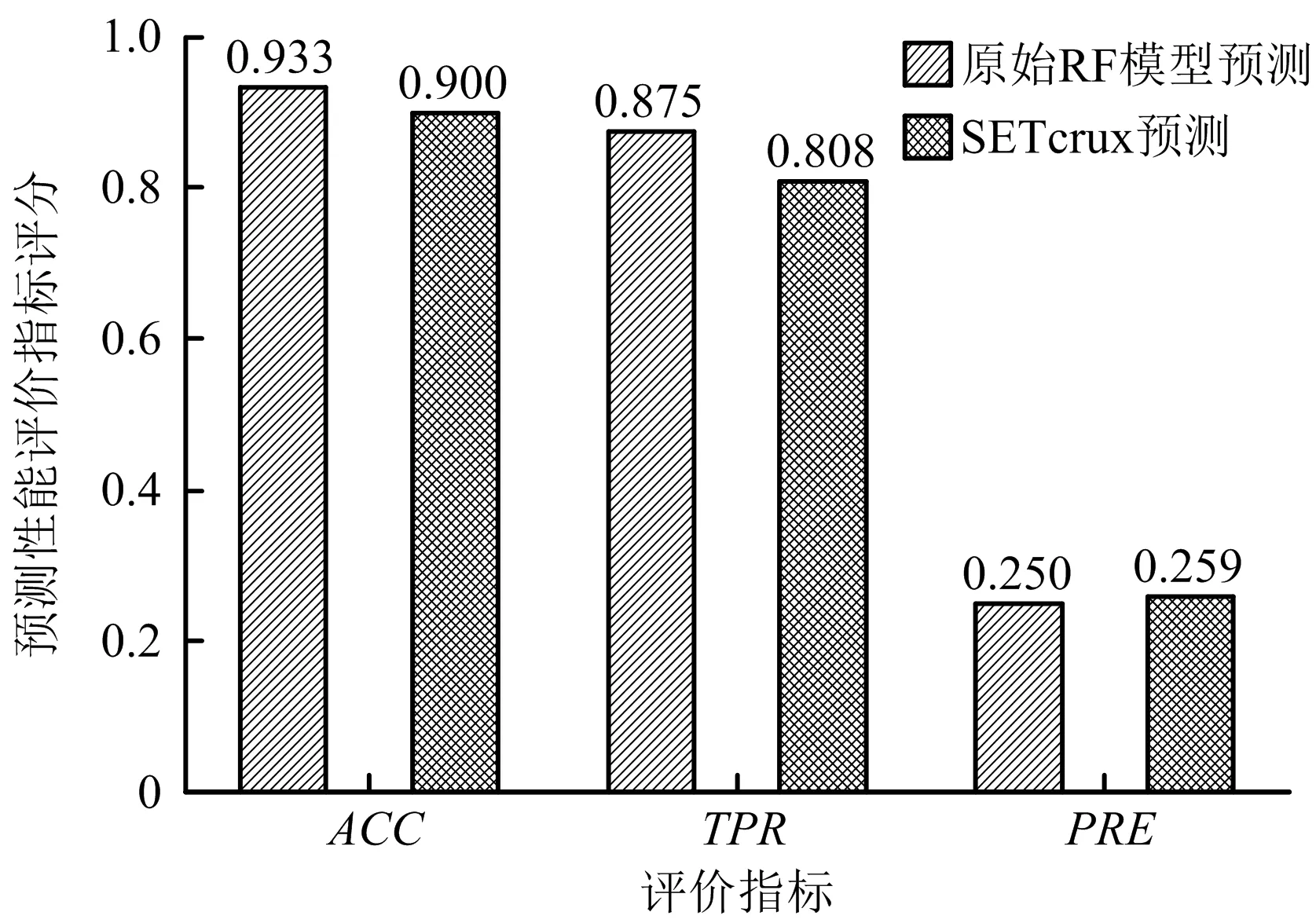
图13 分类精度对比Fig.13 Comparison of classification accuracy

3.4 运营隧道风险判别法则

将提取运营隧道风险判别法则知识化，如表2所示。从包含“Tunnel section的”规则来看，出现“隧道入口过渡段+隧道交安设施不合理或路面结冰或驾驶员违规驾驶及车辆方向失灵”以及“隧道出口过渡段+隧道路面潮湿及驾驶员超速驾驶”时，将发生严重的交通事故，运营风险提高。因此，对于隧道运营者，要避免以上不利因素的组合，即确保隧道内部照明合理并减轻洞内外明暗差异；提前预警由于降雪、低温等特殊天气导致路面积雪、暗冰并及时处理，避免车辆失控导致严重交通事故发生。