基于CNN-GRU的瓦斯浓度预测模型及应用*
2022-10-17李树刚薛俊华
刘 超,雷 晨,李树刚,薛俊华,张 超
(1.西安科技大学 安全科学与工程学院,陕西 西安 710054;2.西部矿井开采及灾害防治教育部重点实验室,陕西 西安 710054)
0 引言
煤炭是我国一次性能源消费的重要支柱,影响国内经济发展和能源安全[1-2]。频发的矿井瓦斯灾害,给煤炭行业造成重大损失并严重威胁人们生命安全。目前,大部分煤炭企业已经配备成熟的安全监测系统,但其功能仅限于短期识别和应对灾害,未能充分利用现有监测数据,导致矿井瓦斯灾害预测能力不足。因此,迫切需要引入新的方法和技术,通过对监测数据深度挖掘分析,实现对瓦斯浓度精准预测,提高煤矿瓦斯灾害预警能力,降低矿井瓦斯灾害造成的经济损失,保护人们生命安全。
为实现瓦斯浓度预测,国内外学者开展研究:文献[3-6] 提出基于相空间重构理论、自适应混沌粒子群优化理论与支持向量机(SVM)相结合的瓦斯浓度预测方法;郭思雯等[7]提出基于自回归集成移动平均模型的瓦斯浓度预测方法;武艳蒙等[8]利用SVM和差分进化(DE)算法建立预测模型,并基于马尔可夫链的残差修正预测瓦斯浓度变化趋势;吴海波等[9]提出基于Spark Streaming框架的流回归瓦斯浓度预测方法;Marek等[10-11]将ARIMA模型、K-临近和模型树法相结合,对瓦斯浓度进行预测,并且提出局部线性与差分整合移动平均自回归模型组合的瓦斯浓度预测方法。上述研究方法均集中于单特征学习且数据集相对较小,因瓦斯浓度数据具有动态和非线性,使得上述方法在精确度和适用性方面表现不佳。
伴随云计算和人工智能发展,门控循环单元(Gated Recurrent Unit,GRU)在智能装备制造[12]、图像识别[13-14]、能源预测[15-16]和智能交通[17]等方面得到广泛应用。GRU是传统循环神经网络的优秀变体,其最大特点是善于处理复杂的多维时间序列。鉴于此,本文引入卷积神经网络(CNN),提取瓦斯数据时空特征,构建集时间与空间为一体的多维特征矩阵,将提取的数据信息输入GRU,深度挖掘每个变量间的相互内在关系,并构建基于CNN-GRU的瓦斯浓度预测模型,研究结果在提高瓦斯浓度预测精度同时保证预测时效性。
1 门控循环单元(GRU)
传统神经网络层与层之间无节点连接,在解决时间序列问题上效果较差[18]。循环神经网络与GRU结构原理如图1所示,循环神经网络(RNN)是1种具有反馈结构的网络,在计算当下输出时,隐藏层神经元会将储存单元信息作为部分输入,使输出受先前输出影响。因RNN善于处理时间序列信息,被广泛用于具有时间信息数据挖掘工作。

图1 循环神经网络与GRU结构原理Fig.1 Recurrent neural network and GRU structure principle
长短期记忆(LSTM)是循环神经网络的优秀变体,主要由输入门、遗忘门和输出门组成,输入门控制细胞状态,将信息选择性保留下来,遗忘门将细胞状态中的信息选择性遗忘,输出门针对隐藏层储存单元决定输出信息。同时,在整个过程中通过消除或增强输入神经细胞单元信息控制细胞状态[19]。
门控循环单元(GRU)将LSTM进一步改进[20],结构如图1(d)所示,通过将遗忘门和输入门合并成更新门,改进LSTM的3门设计,目的是减少参数以优化细胞结构,提高运行效率,使得在训练过程中更容易收敛。GRU主要按更新数据信息、数据信息汇总、重置数据信息和数据信息输出4个步骤运行[21]。
1)更新数据信息。更新门控制隐藏层中的记忆信息,将信息进行线性变换,如式(1)所示:
zt=σ(Wz·[ht-1,xt])=σ(Whz·ht-1+Wxz·xt)
(1)
式中:zt为更新门信息;σ为sigmoid函数;t,t-1表示时刻;Wz为当前更新门权重;Whz表示在当前隐藏层状态下更新门权重;Wxz为当前更新门输入信息权重;ht-1为t-1时刻隐藏层状态;xt为t时刻输入信息。
2)数据信息汇总。确定前一时刻和当前时刻信息在隐藏层中遗忘的信息,如式(2)所示:
rt=σ(Wr·[ht-1,xt])=σ(Whr·ht-1+Wxr·xt)
(2)
式中:rt为重置门信息;Wr表示当前重置门权重;Whr表示在当前隐藏层状态下重置门权重;Wxr表示当前重置门输入信息权重。
3)重置数据信息。控制当前信息利用度和产生新记忆信息的数据量,作为输入继续向前传递,如式(3)所示:
(3)
式中:W表示权重;ut表示重置信息;tanh为双正切函数变换;Wh表示当前隐藏层权重;Wx表示输入信息权重;符号*表示线性变换。
4)数据信息输出。利用更新门计算当前输入信息,如式(4)所示:
ht=zt*ht-1+(1-zt)*ut
(4)
式中:ht表示t时刻隐藏层状态。
2 瓦斯浓度预测模型构建
2.1 CNN-GRU预测模型
CNN-GRU预测模型结构如图2所示,主要由输入层、CNN层、全连接层、GRU层和输出层5部分构成。输入层是将某一时刻影响瓦斯浓度因素与瓦斯浓度数据本身串联成1个向量,利用滑动窗口形成新的时间序列数据;CNN层是对输入序列数据进行特征提取,CNN单元能够通过卷积核运算自动提取数据局部变化趋势,线性合并多组数据的抽象时空特性,提取多维时间序列特征;全连接层是将经多次核卷积后形成的抽象特征进行汇总,将卷积层输出的多维特征矩阵转化成一维向量,最后把转换后的一维向量完整的传递给GRU网络;GRU层主要是对CNN层提取的特征向量进行充分学习,记忆长期依赖的历史数据,最终得到其内部特征变化规律,以此对未来瓦斯浓度数据进行预测;输出层是将预测值反归一化后输出。
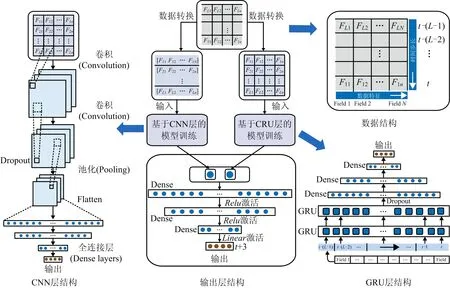
图2 CNN-GRU组合模型结构Fig.2 Structure of CNN-GRU combined model
2.2 CNN参数设置
考虑瓦斯浓度数据的复杂性和CNN提取能力,将2D-CNN(二维卷积)作为网络结构,以保证预测效果的稳定性。CNN特征识别功能有利于在不同层次的高维时间序列数据中自动提取共同特征,将数据转换为沿时间轴的网格,利用CNN进行时间序列数据处理,如图2所示。将最近L个日期的瓦斯浓度和具有N维属性影响因素数据转换成网格,在输入层后仅连接2层卷积层,并采用Dropout技术防止过拟合,如图2所示,目的是避免数据在通过池化层时丢失重要特征,以较少的层数快速提取高维特征。在连续卷积和池化后,通过Flatten层将数据降维,最后设置神经元数量分别为128,64,32的3层全连接层。CNN主要参数见表1。

表1 CNN参数设置Table 1 Parameters setting of CNN
2.3 GRU参数设置
采用多对一和一对一2种回归形式的2层GRU结构,使模型在最后1个时间步长前,对输入的时间序列均能产生新的记忆状态。由图2可知,基于GRU的模型结构,其实现方法包括以下3个步骤:1)将数据以一对一的模式输入到第1层GRU,并且每个时间步长的记忆状态已经更新;2)第1层GRU的输出以多对一的模式进入第2层GRU;3) 在第2层GRU输出后进入全连接层。叠加2个层是为了预测每个时间步长,初步预测序列中趋势,以帮助模型学习更高水平的时域特征表达。同理,建立3层全连接层,神经元数量分别设置为128、64、32,具体参数设置见表2。

表2 GRU参数设置Table 2 Parameters setting of GRU
3 实例应用
3.1 数据来源与预处理
本文数据来自玉华煤矿2021年3月11日至2021年3月21日2407工作面每5 min的日常生产监测数据,包括瓦斯浓度、温度、流量、负压4个变量,共3 041组,数据特征如图3所示。将数据按7∶3比例划分为训练集和测试集,用近似平均值补充缺失数据,删除异常数据。为便于计算并提高预测精度,采用MinMaxScaler方法规范化,将数据缩放到[0,1],如式(5)~(6)所示:

图3 原始数据箱体图Fig.3 Diagram of original data box
(5)
Xscaled=Xstd×(Max-Min)+Min
(6)
式中:Xstd表示放缩标准;X为数据;XMax,XMin表示数据最大值和最小值;Max,Min为数据缩放后的最大值和最小值;Xscaled表示最终放缩结果。处理后数据如图4所示。
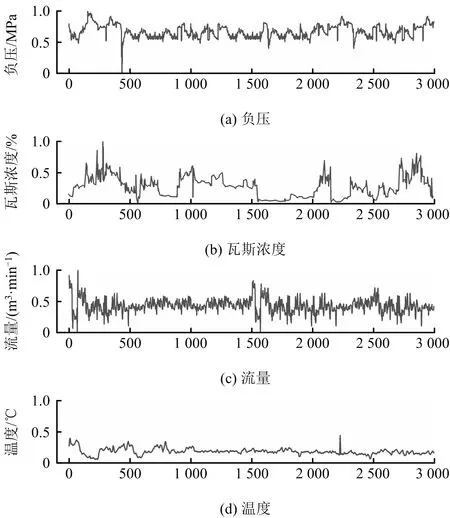
图4 处理后数据Fig.4 Processed data
皮尔逊分析是衡量不同变量之间相关程度,其运行原理如式(7)所示[22]:
(7)

本文运用SPSS软件对采集的4个变量进行皮尔逊相关性分析,结果见表3。由表3可知,温度与瓦斯浓度呈高度相关,流量和负压与瓦斯浓度呈中度相关。因此,本文选择瓦斯浓度、流量、温度和负压4个变量作为预测模型的输入是合理的。

表3 各影响因素相关性分析结果Table 3 Correlation analysis results of each influencing factor
本文实验采用Python3.7开发语言、Pycharm社区版集成环境,GRU模型和CNN模型均来自Keras2.1.5,计算机配置为CPU(i7-8550),显卡RX550,内存8GB。通过2个评价指标衡量模型预测精度。
平均绝对误差(MAE)如式(8)所示:
(8)
均方根误差(RMSE)如式(9)所示:
(9)
式中:fi,yi分别为预测值和真实值;m为样本个数。
3.2 模型运行效率对比
为比较不同模型达到最优结果时的运行效率,将CNN-GRU组合模型与传统机器学习模型LSTM和GRU进行比较,采用训练集导入模型,在训练过程中,当损失函数值连续增加或无明显减少时,提前终止训练,经过3次训练后结果如图5~6所示,LSTM、GRU和CNN-GRU的平均训练轮次(Epoch)分别为325,200,159次;LSTM、GRU和CNN-GRU的平均训练时间分别为590,371,241 s;CNN-GRU的运行效率比LSTM和GRU分别提高59.15%,35.04%,并且CNN-GRU模型需要的训练轮次最少,较大幅度降低内存消耗。
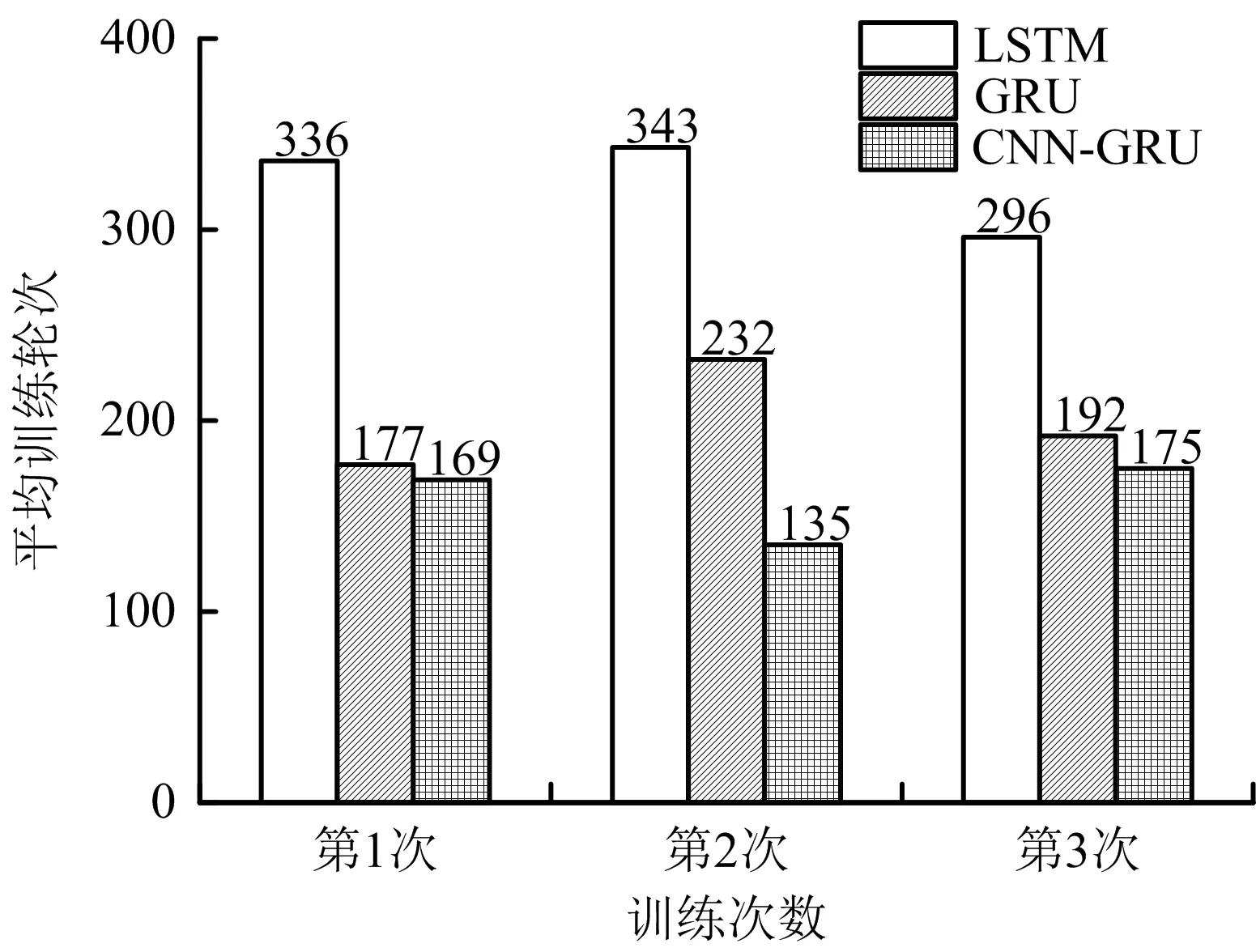
图5 3种模型训练时间和训练轮次比较Fig.5 Comparison on training time and training round of three models
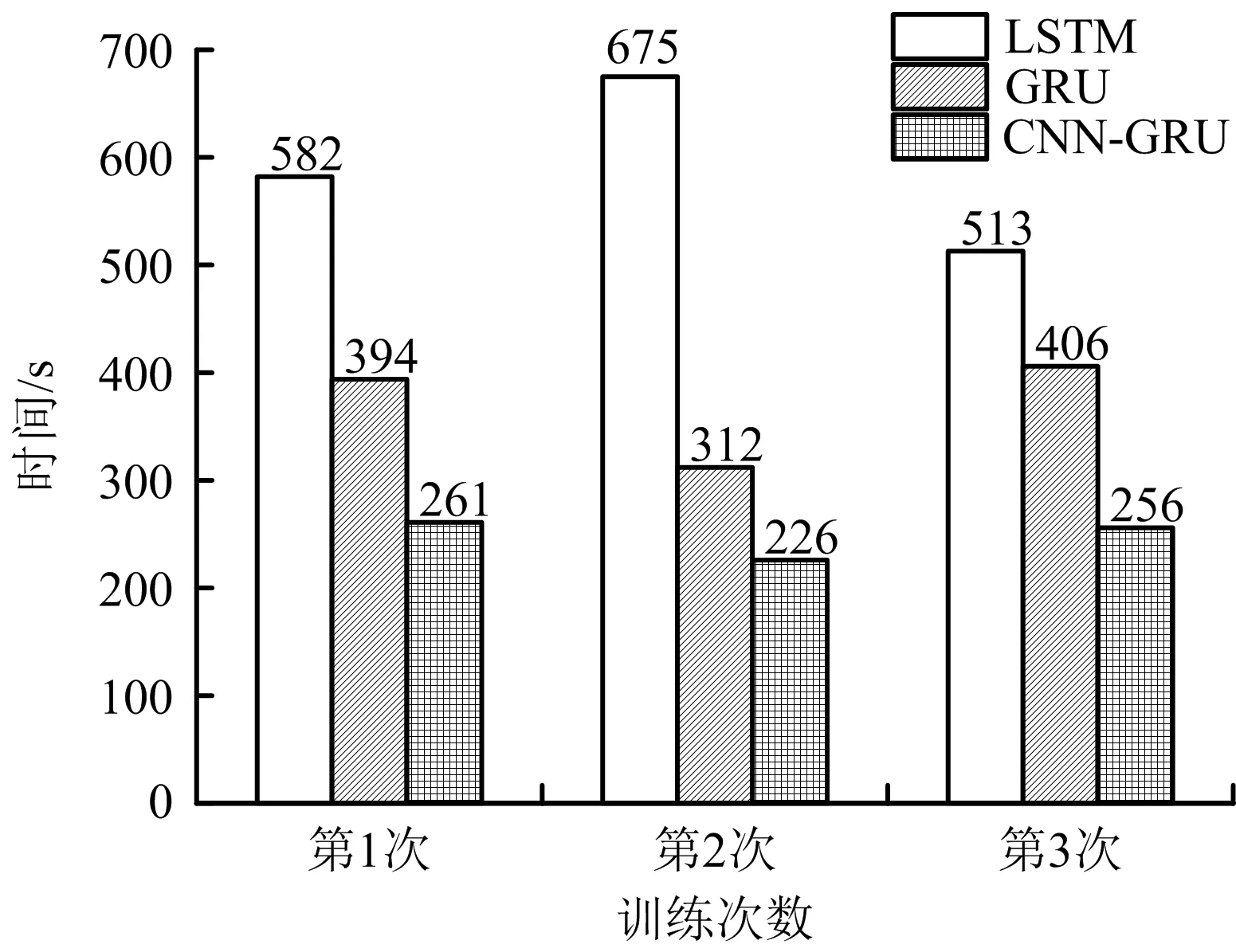
图6 3种模型训练时间比较Fig.6 Comparison on training time of three models
3.3 模型精度对比
LSTM、GRU和CNN-GRU 3种模型测试误差结果如图7所示,CNN-GRU测试过程中平均绝对误差和均方根误差均优于LSTM和GRU,同时CNN-GRU的平均绝对误差误差主要集中在0.045~0.052,均方根误差主要集中在0.007~0.01,误差波动范围更小,具有较高的稳定性。

图7 3种模型预测结果误差对比箱线Fig.7 Box line for comparison on error of prediction results by three models
LSTM、GRU和CNN-GRU的整体预测结果如图8~10所示,CNN-GRU可有效预测瓦斯时间序列的峰谷值,在整体预测趋势上优于LSTM和GRU。3种模型详细误差对比见表4,CNN-GRU的平均绝对误差和均方根误差相对最低,分别可降至0.042和0.006,平均误差分别为0.047和0.008,相比于LSTM降低46.6%,55.6%,相比于GRU降低37.3%,50.2%。
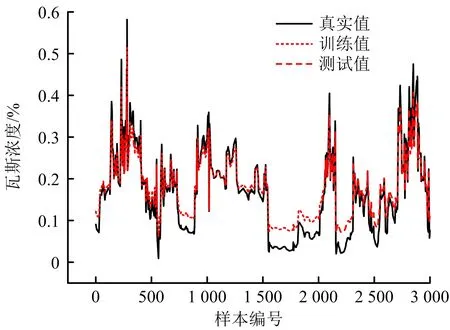
图8 LSTM模型预测效果Fig.8 Prediction effect of LSTM model
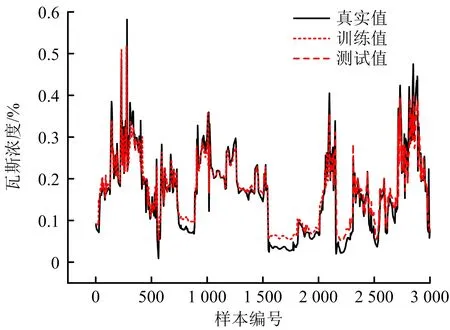
图9 GRU模型预测效果Fig.9 Prediction effect of GRU model

图10 CNN-GRU组合模型预测效果Fig.10 Prediction effect of CNN-GRU model
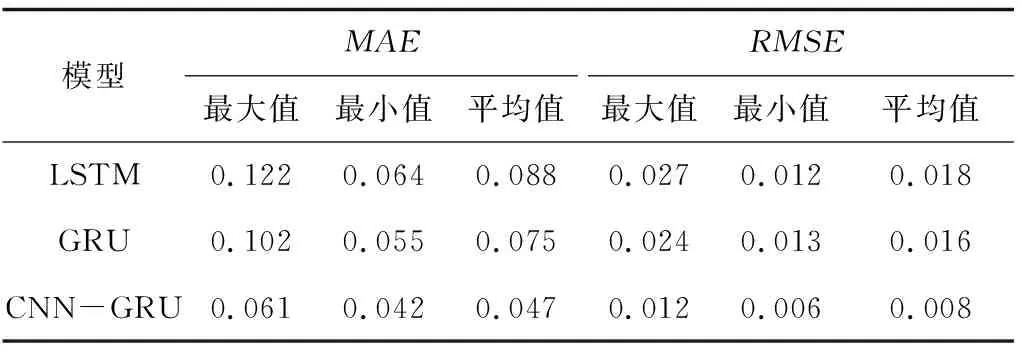
表4 3种模型预测结果误差Table 4 Prediction results error of three models
4 结论
1)基于CNN-GRU的瓦斯浓度组合预测模型,能够克服传统预测方法的数据特征单一和解决非线性能力差的问题,利用多类型数据对瓦斯浓度进行时序性预测。
2)采用MinMaxScaler和皮尔逊相关性分析对实验数据进行预处理和相关性分析,提高数据质量同时,证明多种影响因素作为模型输入的合理性。
3)CNN-GRU组合模型相比于LSTM、GRU模型有更高的预测精度,平均绝对误差和均方根误差可降至0.042和0.006,更适用于瓦斯浓度时间序列预测,并且在训练过程中所需训练轮次和运行时间相对较少,降低内存消耗,提高预测效率,具有更高的应用价值。
