基于改进遗传算法的导向辊生产调度方法研究

张朝阳，徐莉萍，张增强，刘善惠，李健

基于改进遗传算法的导向辊生产调度方法研究

张朝阳1，徐莉萍1，张增强2，刘善惠2，李健1

（1.河南科技大学 机电工程学院，河南 洛阳 471000；2.西安理工大学 印刷包装与数字媒体学院，西安 710000）

研究导向辊生产车间中的调度优化问题，有利于缩短工件的完工时间，提高产线生产效率。以某导向辊生产车间为研究对象，以最小化最大完工时间为目标建立数学模型。针对该导向辊生产车间的实际工况，提出一种改进的遗传算法进行求解。通过对10种不同尺寸的导向辊进行生产调度，分别采用改进的遗传算法和传统遗传算法进行试验分析。改进的遗传算法相比传统遗传算法寻优能力更高，工件的完工时间从139 min缩短为113 min，缩短了18.7%左右，生成了完工时间为113 min的生产调度甘特图。与传统遗传算法相比，改进的遗传算法在导向辊生产调度优化中具有更高的全局优化能力和寻优精度。

导向辊；生产调度；改进遗传算法；最大完工时间

随着个性化印刷品需求的迅猛增加，印刷装备的生产模式逐渐向多品种、小批量的方向转变，这为印刷装备零部件的生产调度带来了难题。如何在规定的时间内，合理安排生产任务，成为印刷装备精益生产中的关键问题。导向辊作为印刷装备中种类最多、用量最大的核心零部件，占用了设备制造企业大量的生产资源。如何通过优化导向辊加工车间生产调度，合理安排工件工序和加工设备来缩短生产时间和降低成本，成为了企业面临的重大挑战。

目前，生产调度优化问题的求解算法主要集中在智能优化算法中，如人工蜂群算法[1]、模拟退火算法[2]、混合差分进化算法[3]、蛙跳算法[4]、蚁群算法[5]等已被运用到各种生产调度问题中。遗传算法（Genetic Algorithm, GA）作为智能算法中一种常见性算法，因其编码简单、性能优良，被广泛应用在生产调度中。刘晨等[6]针对面向订单模式的印刷企业，设计遗传算法的编码方式，实现缩短生产周期的同时，提高资源利用率。梁艳杰等[7]针对混流加工和流水装配2个阶段的调度问题，以加工产线最大完工时间和装备产线最大完工时间为目标，实现双产线双目标优化。郝琪等[8]针对印刷企业的生产排产问题，采用遗传算法用于缩短印刷周期，提高设备的利用率。雷斌等[9]针对生产转向架的混流装配车间，构建以完工时间为目标的数学模型，采用粒子群和遗传算法的混合算法进行优化求解。龚鼎等[10]针对轴类零件的生产车间，根据生产需求，从单台设备的切削用量和能耗方面进行建模，通过消除瓶颈工序，实现产线优化的目的。于蒙等[11]针对设备负载的均衡问题，提出改进的遗传–粒子群算法，并基于实际汽车生产线数据进行验证算法的有效性。孔琳等[12]基于混合流水车间调度中的机床加工特性，采用遗传算法解决车间生产中的设备选择和调度目标相匹配的问题，基于权重法提出4种不同类型的调度方案。宋存利等[13]针对混流车间的最大完工时间的单目标问题进行建模，提出贪婪交叉和变异算子的改进贪婪遗传算法，通过正交试验确定算法参数，并与已有算法进行求解比较，证明了该算法的有效性。

文中针对导向辊生产中种类多、零件多的特点，以最小化最大完工时间为优化目标，根据导向辊车间生产情况对遗传算法进行改进，实现对导向辊加工车间的调度优化，并与传统遗传算法进行比较，以验证改进遗传算法的有效性。

1 导向辊生产工艺分析

1.1 典型导向辊结构

导向辊大体可以分为有钢轴导向辊和无钢轴导向辊2类。典型的有钢轴导向辊由钢轴、铝堵、辊筒等3个部分组成，其结构见图1。不同型号的有钢轴导向辊组成的零部件基本相同，其区别主要在于尺寸和表面导向槽的类型。

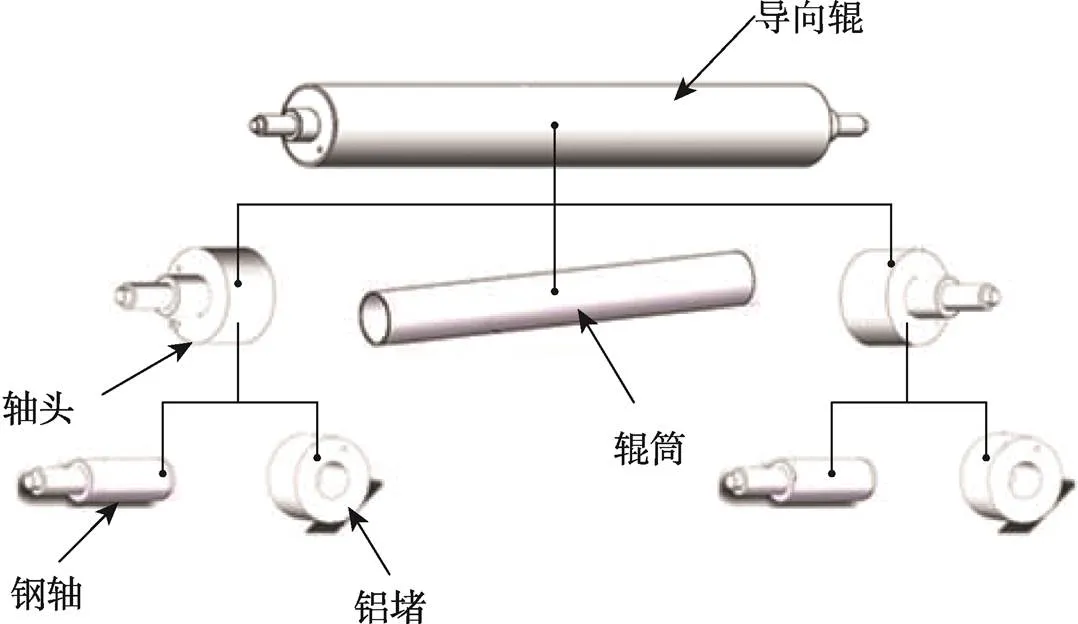
图1 导向辊结构简图

1.2 导向辊生产工艺流程

导向辊生产为混合流水线生产方式，即不同类型、尺寸的导向辊有着大致相同的加工工艺和顺序。以有钢轴导向辊的加工为例，共有8道生产工序，其工艺流程见图2。

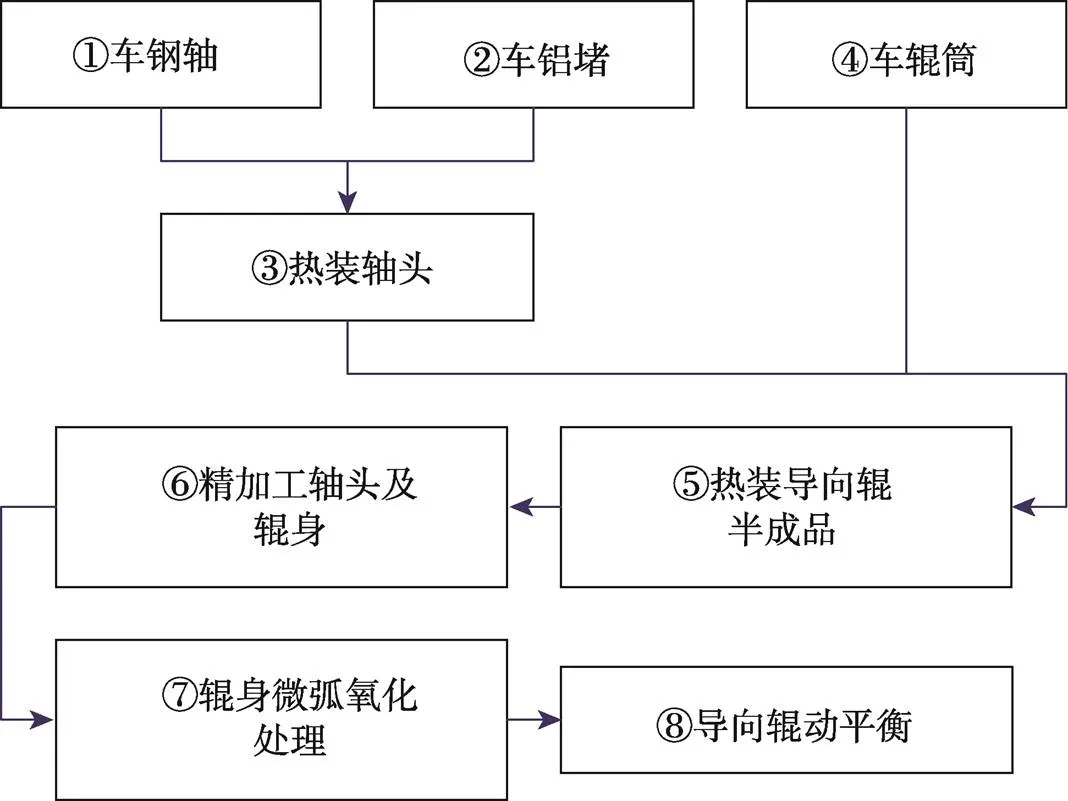
图2 导向辊生产工艺流程

传统的加工方式是以流水线形式进行生产，即每道工序可选择的加工机器仅有1台，每个工件按照加工工艺顺序在对应的机器上进行加工，以表1中的生产数据为例，工序4和工序7存在2台并行机，并且每台机床只能加工1种工序，其加工调度图见图3。

表1 工件加工工艺参数

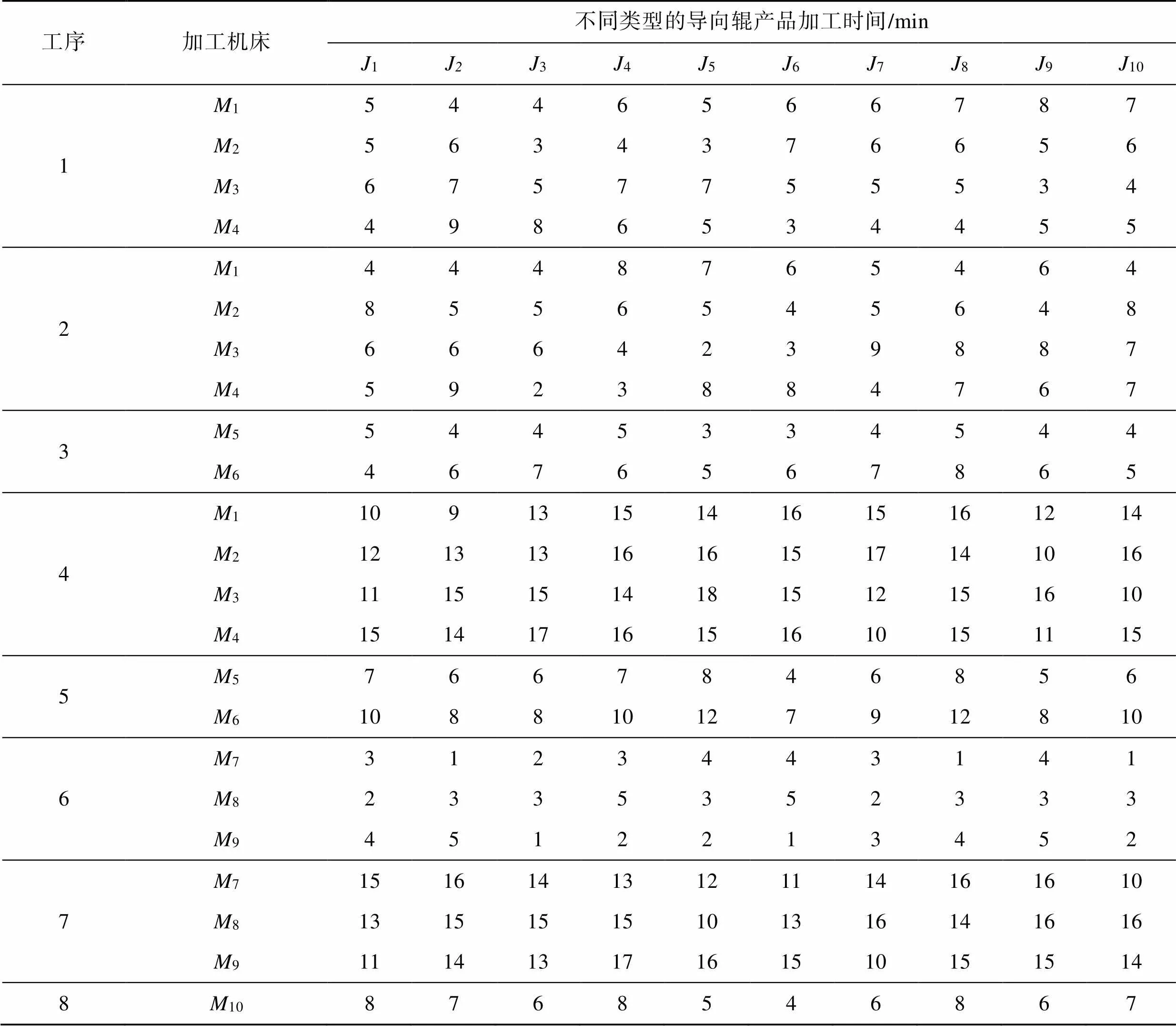
Tab.1 Technological parameters of workpiece processing

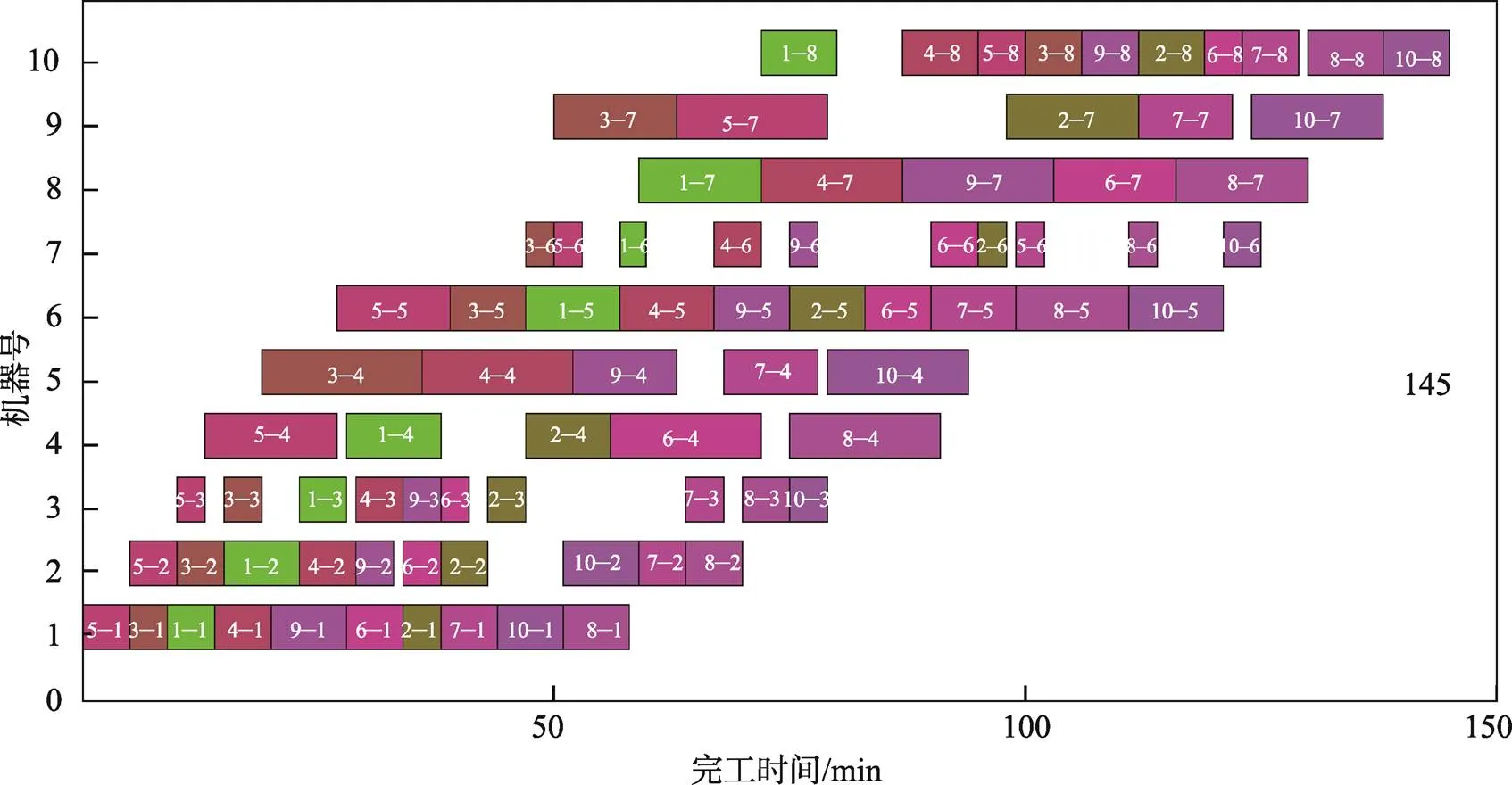
图3 传统调度方式甘特图

从图3中可以看出，传统的生产方式在生产8件导向辊的过程中，整个车间设备利用率很低，并没有合理化利用整个车间设备的生产资源，如机器7的空闲时间过长，导致整个生产时间过长，达到145 min。此外，并没有发挥机床可以加工多种工序的功能，因此对整个车间的各种设备进行重新分配和利用，通过提高整个车间的生产柔性，以达到缩短完工时间、提高生产效率的目的。

2 问题建模与描述

2.1 导向辊生产问题描述

导向辊的生产方式为混流生产方式，可表述为：个工件在台机床上进行加工，其个工件有大致相同的加工工序；每个工件有道工序，至少有一道工序存在2台以上机床可以选择；通过安排工件的加工工序和对应的机床，使工件在最短时间内完成加工，提高生产效率。在建立模型之前，作出假设如下。

1）不考虑工件缓存区，原材料准备充足且不考虑机床故障问题。

2）不考虑工件的运输时间及机床的换刀和装夹时间，即工件在加工之后可以立即送到下一个指定工位之上。

文中所研究的导向辊有8道生产工序，10种不同导向辊类型的工件在10台机床上进行加工，即=10、=10、=8。

2.2 建立导向辊生产模型

为建立导向辊生产的数学模型给出表2所示的符号说明。

表2 导向辊数学模型有关符号说明

Tab.2 Relevant symbols of mathematical model of guide roller

以工件的最大完工时间即所有机床完成加工的时间为目标，建立其数学模型如下。

(1)

约束条件为：

(2)

(3)

(4)

式（2）表示工件应该按工序顺序加工，下道工序的开始加工时间应大于该道工序的结束加工时间；式（3）表示工件的一道工序只能由一台机床加工；式（4）表示机床在该道工序完成之后才能进行下一道工序的加工。

3 改进遗传算法设计

3.1 遗传算法

遗传算法是通过计算每个染色体的适应度值和多次迭代来求取最优解。一般情况，适应度函数值与导向辊生产的目标函数有关，即为式（1）。这里是最小值问题，目标函数值越小，对应的适应度值就越高。通过选择、交叉和变异操作进行迭代，完成寻优。

遗传算法中单一的染色体在求解生产调度中无法准确表达问题的解，对单一染色体采用2段编码表示，每段表示不同的含义，来实现生产调度问题的优化求解，遗传算法传统交叉方式是随机进行交叉，容易产生非法解，基于此，采用POX交叉方式避免非法解的产生，同时在变异操作方面基于编码方式采用工序和机器双变异的方式，提高算法搜索效率和求解精度。改进遗传算法流程见图4。

3.2 算法主要步骤

3.2.1 编码方式

文中采用基于工件工序和加工机床的两段式整数编码方式。每条染色体的基因数量即为160个，前80个为工序基因，后80个为加工机床基因。因160位基因编码过长，举一个简单的例子进行说明：假设共有3个工件计6道工序，在3台机床上进行加工，每条染色体共有12个基因为[1,3,1,2,2,3;1,2,2,3,1,1]，前6位代表工件的工序，其对应数字表示工件的名称，该数字第几次出现代表工件的第几道工序；后面的6位表示与前6位工序相对应的工序的机床编码，编码方式见图5。

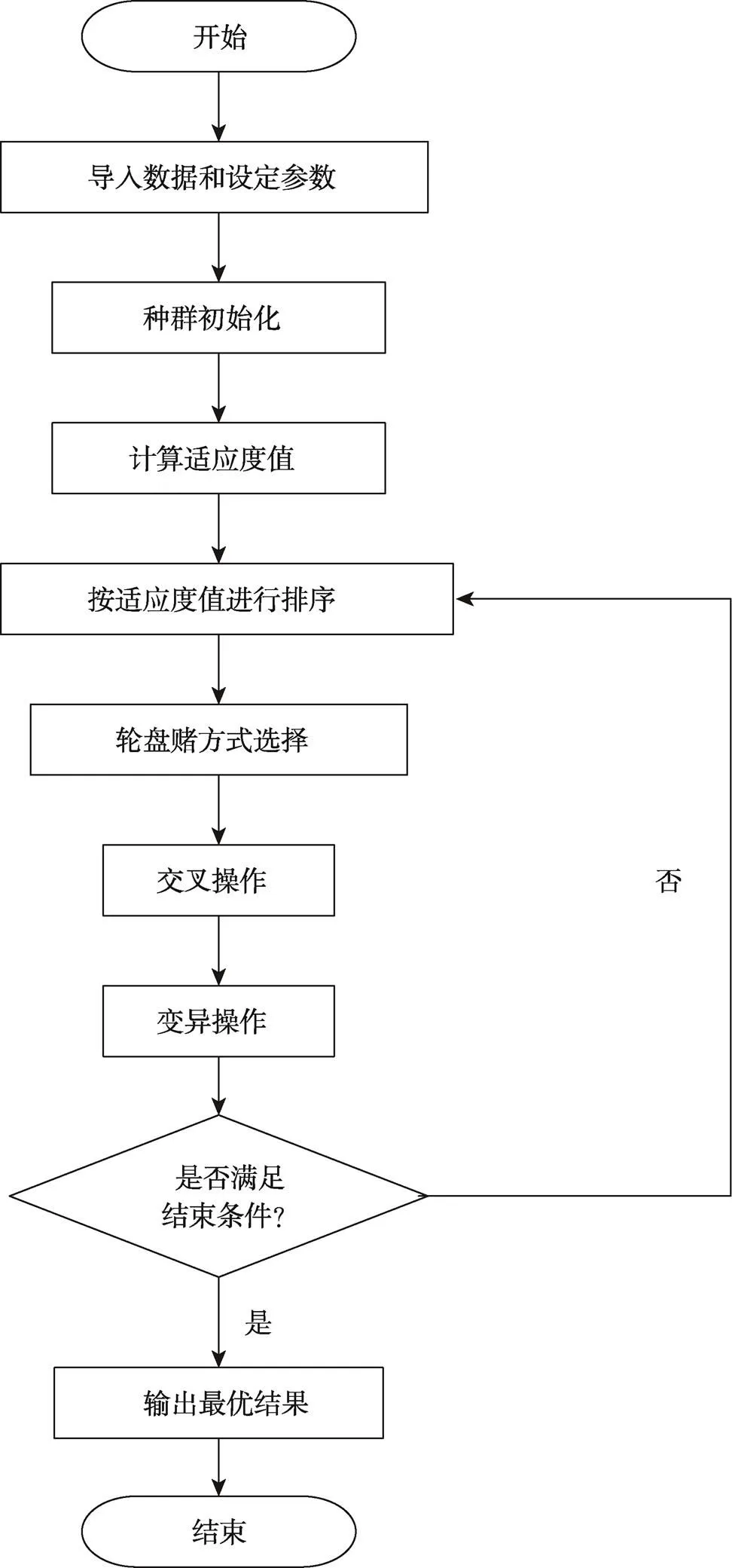
图4 遗传算法流程

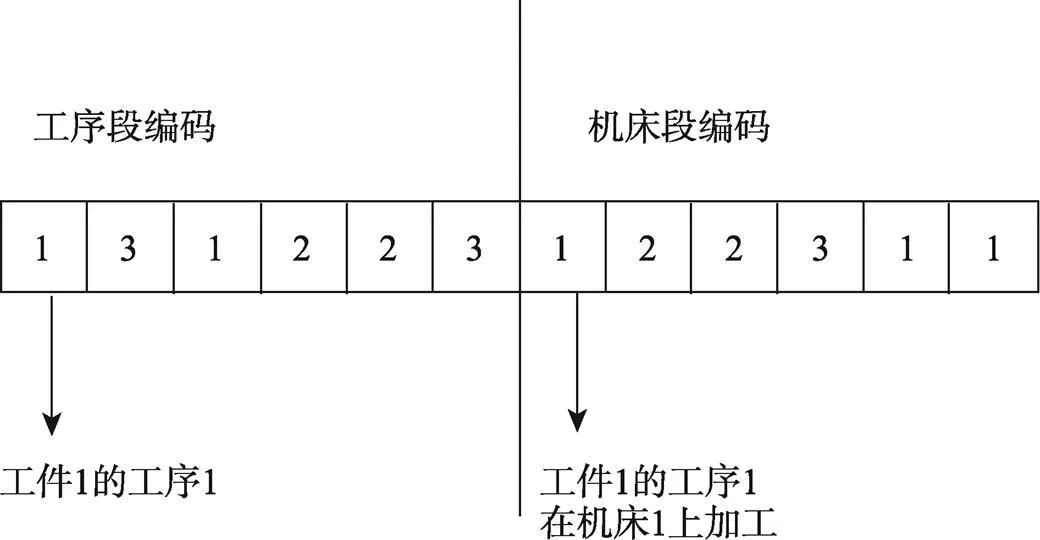
图5 工序和机床编码方式

3.2.2 种群初始化

文中采用随机生成法和完工时间最小法2种规则初始化种群，其生成种群规模分别为60%、40%，提高其初始解的质量的同时，保证种群的多样性。

完工时间最小法初始化方式主要步骤：随机产生工序部分编码；依次按顺序为工序编码选择加工时间最短的机器，若机器不唯一，则在其中进行任选，并按照染色体编码位置进行记录。

3.2.3 适应度值的计算

适应度值计算主要为通过对编码进行解码操作，以此来记录工件的加工时间表，根据种群初始化可得到每条染色体的编码序列和所有工件的完工时间，即可得到染色体的目标函数值，目标函数值越小，代表染色体个体质量越高。

3.2.4 选择操作

(5)

式中：为一个固定常数，与染色体初始的最大值和最小值有关。

3.2.5 交叉操作

交叉操作可以提高种群的多样性，同时也能保留优良的染色体基因，更快得到全局最优解。交叉概率是交叉操作是否发生的决定性因素，通常交叉概率取值为0.6～0.9。

文中采用基于工序的POX（Precedence Operation Crossover）交叉方式[15]，使得子代在继承父代优良特征的同时保证解都是可行的。具体步骤：从种群中随机选择2条染色体作为父代，可以记为1和2，首先根据工件集生成2个子集，满足互补关系，记为1和2，选择包含工件数最少的子集，假设1包含的工件数最少，复制1中包含1的工件编码到子代1编码中的相同位置，复制2中包含1的工件编码到子代2编码中的相同位置；之后复制1中包含2的工件编码按顺序插入到2中，复制2中包含2的工件编码按顺序插入到1中，对机床编码进行相应的位置变化即可。基于工序的POX交叉方式见图6。

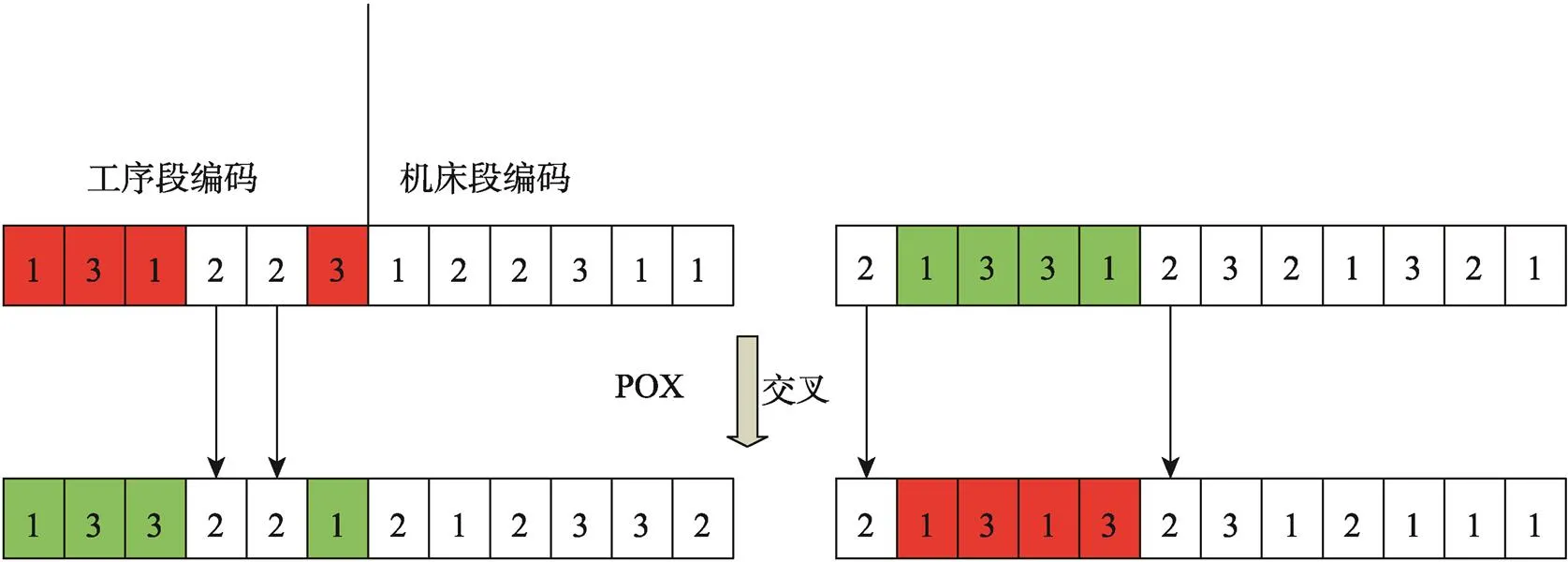
图6 工序编码交叉方式

3.2.6 变异操作

变异操作是为了增加搜索空间，避免算法陷入局部最优。变异操作发生的机会很小，一般变异概率取值为0.001～0.1。文中采用工序基因变异和机床基因变异来执行变异操作。工序变异操作见图7，该工序编码为[1,3,1,2,2,3]，随机选择其中编码总数的一半，对其进行随机排序，并按顺序放回到工序编码的空位置中，得到新的工序编码[2,3,1,3,2,1]；机器变异操作见图8，该机器编码为[1,2,2,3,1,1]，随机选择一个位置，该位置的数字所代表的工序对应的机器集中进行随机变换，选择第4个位置编码3，在其机器集[1,2,3]中随机选择一个新编码，其位置的新编码为2，得到新的机器编码为[1,2,2,2,1,1]。

(3) 对任意B,C∈Γ(CSI(X)),若F⊆B∪C,由τCSI⊆τ,故B,C∈Γ(X),又F∈CIrr(X),于是F⊆B或者F⊆C,从而F∈CIrr(CSI(X))。

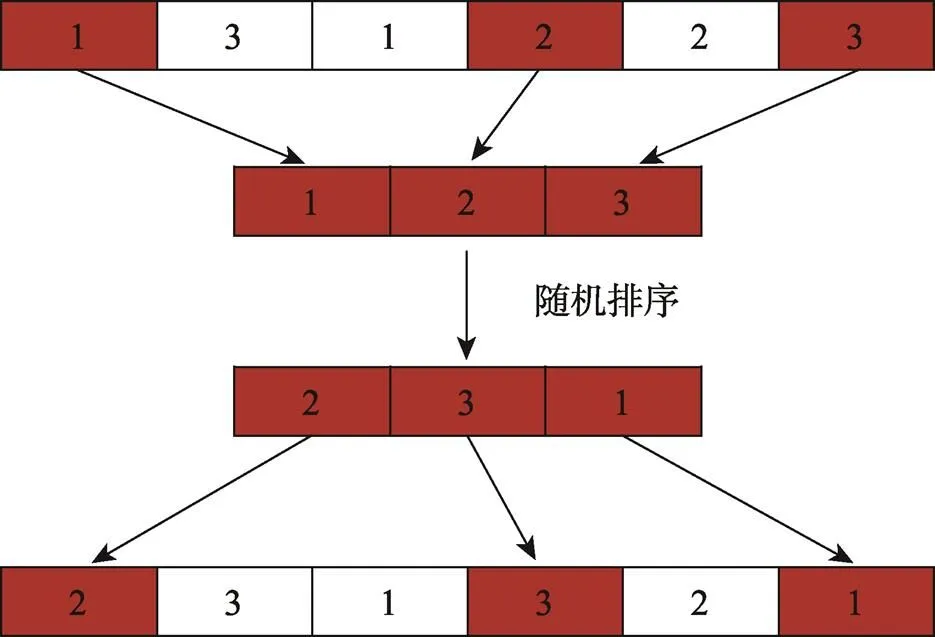
图7 工序编码变异方式

4 试验分析

为了验证所提的改进遗传算法在FJSP中的有效性，以传统编码和单点交叉相结合的方式进行编码，采用改进遗传算法对导向辊生产车间的算例进行对比验证，导向辊生产车间的工件加工工序和对应加工机床的加工时间见表1。

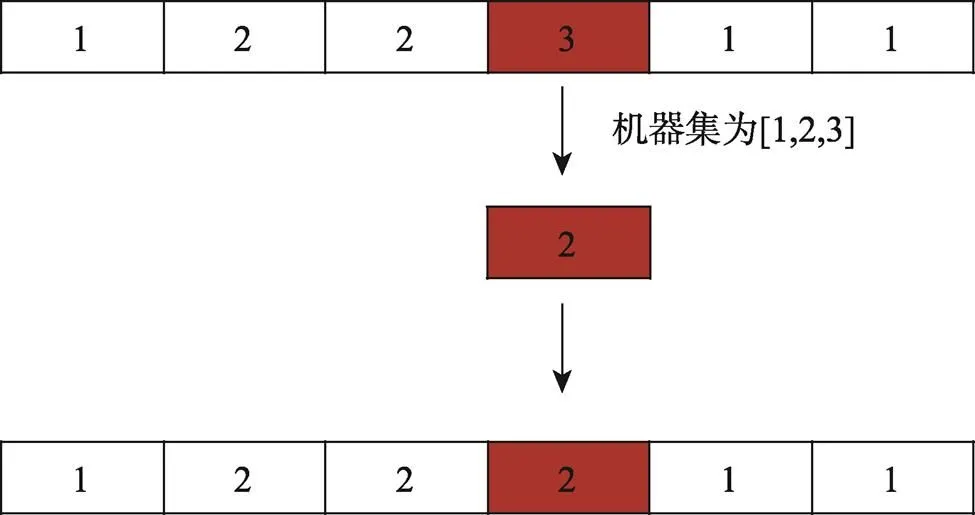
图8 机器编码变异方式

在Matlab R2016a环境中，分别采用改进的GA和传统的单点交叉方式的GA进行调度优化求解。

对改进遗传算法参数进行设置，设置其种群数目为200、最大迭代次数为200、选择概率为0.8、交叉概率为0.7和变异概率为0.1.

改进遗传算法在求解导向辊调度优化的算法步骤如下。

输入：导向辊加工参数。

输出：最大完工时间和调度甘特图。

1）初始化。设置改进遗传算法的初始参数，并导入导向辊的加工信息数据，随机生成个体120个，并基于最小时间完工法生成个体80个，共计200个染色体。

2）计算适应度值。首先对染色体编码进行解码操作，按照解码顺序记录工件的加工时刻表和机器位置，得出工件的最大完工时间值，即适应度值，之后按照适应度值大小进行染色体排序。

3）选择操作。采用轮盘赌的方式进行染色体个体筛选。

4）交叉操作。随机选择2个染色体进行工序部分的POX交叉。

5）变异操作。随机选择1个染色体，对工序部分进行随机排序，机器编码在工序集中随机选择1个位置。

6）判断是否达到最大迭代次数，若达到，则输出最优染色体的适应度函数值，即最大完工时间，并绘制调度甘特图，否则转到步骤2。

在上述算法参数条件下分别采用遗传算法和改进遗传算法进行20次试验，其调度结果对比见图9。

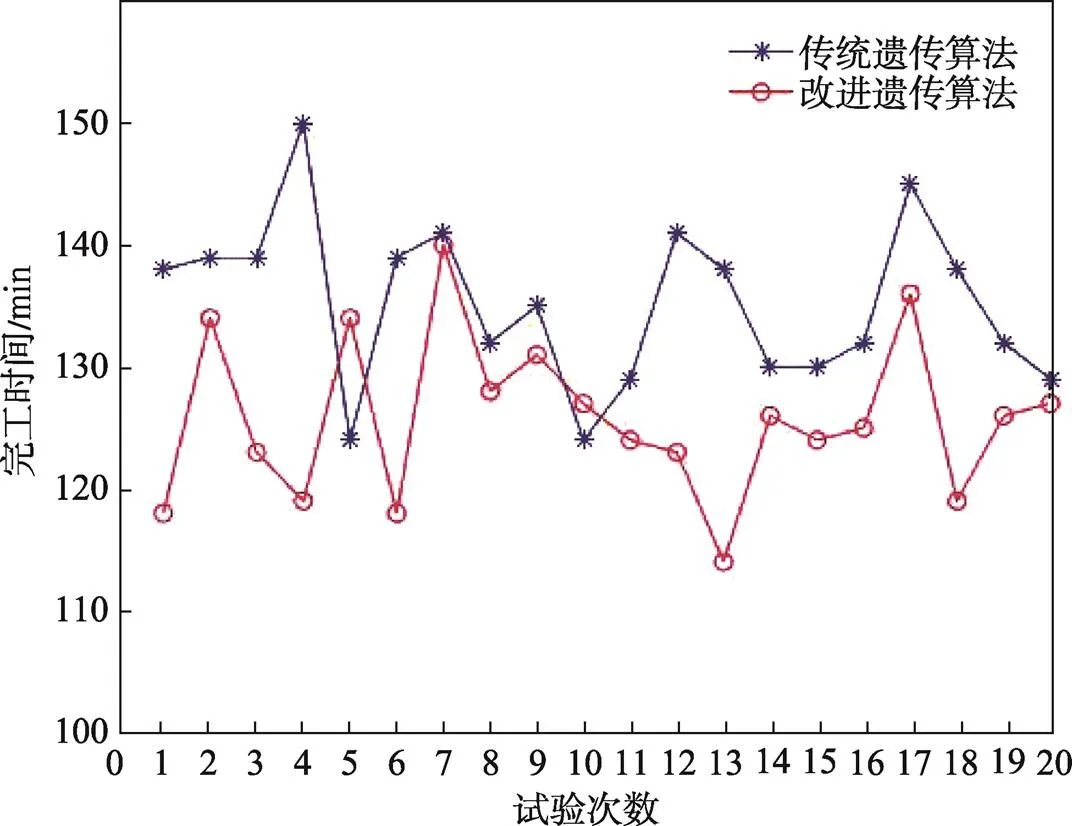
图9 改进遗传算法和遗传算法试验结果对比

由图9可知，在相同的参数设置下，改进GA较传统GA在结果寻优能力上较好，出现最优解的次数较多。13次仿真得出的进化代数曲线见图10，从图10中可知，改进遗传算法在100代之后才完成收敛，与传统遗传算法在80代左右收敛相比，改进遗传算法收敛速度较慢，但在求解精度上有所提升，最大完工时间从139 min缩短为113 min，缩短了约18.7%。

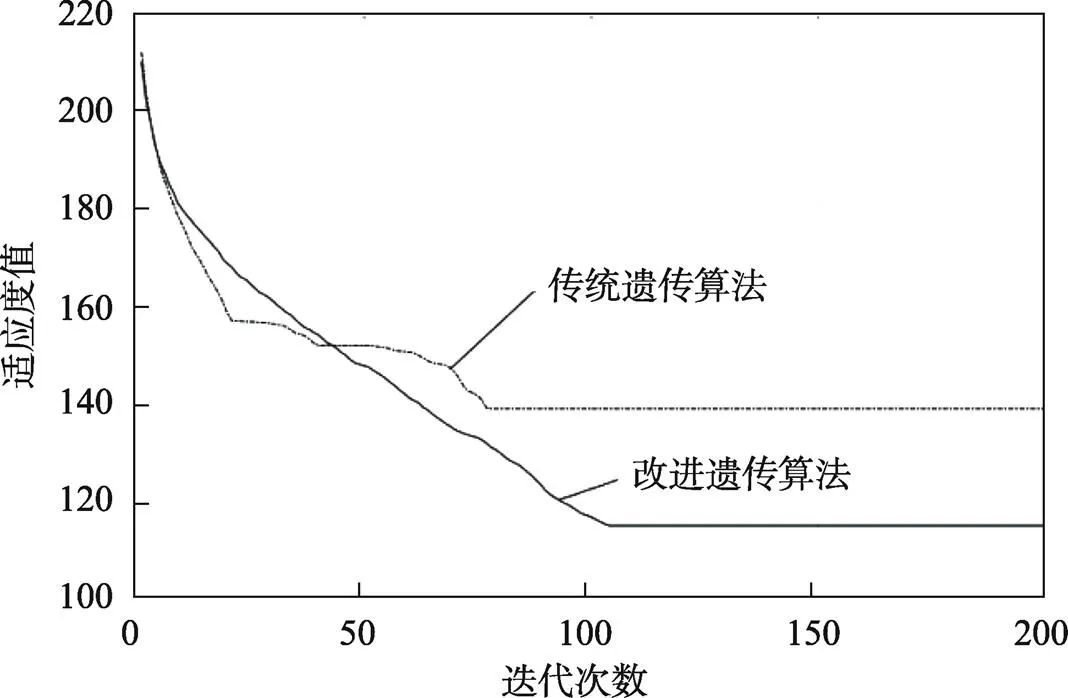
图10 改进遗传算法和遗传算法进化曲线对比

改进遗传算法得到的最优调度甘特图见图11，其完工时间为113 min。以图11中2–3举例说明：首位数字表示工件2，第2位表示工件2的第3道工序，对应的纵坐标表示加工机床5。

图11的仿真结果与传统调度方式相比，整个生产的完工时间由145 min降低为113 min，时间缩短了22.1%，为企业提高生产效率提供了有力的改进措施。

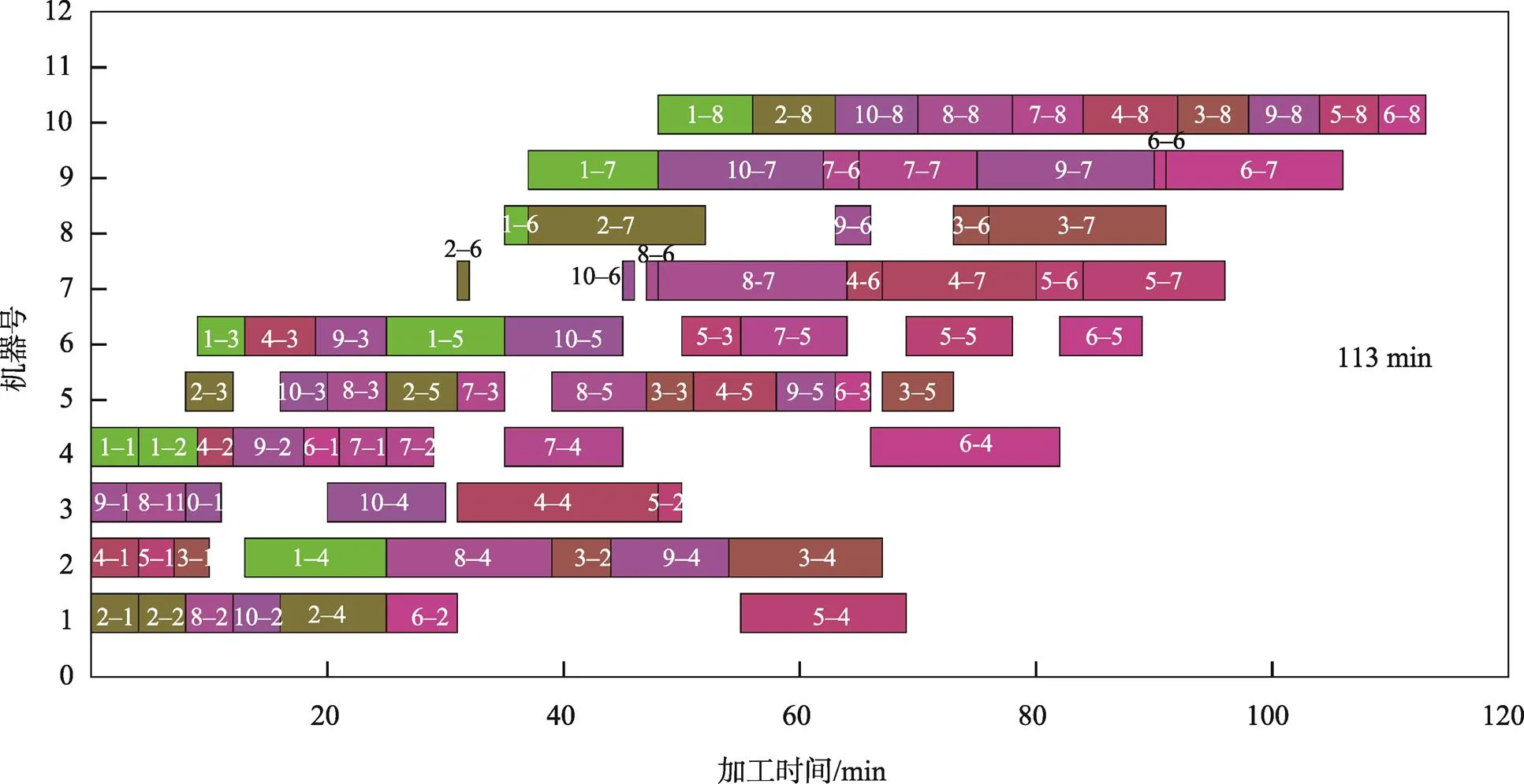
图11 最优调度甘特图

5 结语

文中通过对某公司导向辊加工车间的生产线进行分析，以最大完工时间最小为目标建立数学模型，提出基于POX的工序交叉方式、工序编码变异和机床编码变异方式的改进遗传算法，使得该算法在求解精度上更高。通过对10种不同类型的导向辊生产进行调度优化，结果表明，改进遗传算法在求解精度上比遗传算法的更高，寻优能力更强，但是，由于增加了算法交叉和变异操作的复杂性，在计算时间上会有所增加，导致算法收敛速度有所降低。

[1] SCARIA A, GEORGE K , SEBASTIAN J. An Artificial Bee Colony Approach for Multi-objective Job Shop Scheduling[J]. Procedia Technology, 2016, 25: 1030-1037.

[2] ZANDIEH M, KHATAMI A R , RAHMATI S. Flexible Job Shop Scheduling under Condition-based Maintenance: Improved Version of Imperialist Competitive Algorithm[J]. Applied Soft Computing, 2017, 58: 449-464.

[3] 赵燕伟, 张立萍, 张景玲, 等. 加工装配式流水车间节能调度建模与优化[J]. 中国机械工程, 2014(16): 2196-2203.

ZHAO Yan-wei, ZHANG Li-ping, ZHANG Jing-ling, et al. Modeling and Optimization of Process-Assembly- Type Flow-Shop Scheduling Problem with Energy Saving[J]. China Mechanical Engineering, 2014(16): 2196-2203.

[4] 雷德明, 王甜. 基于改进蛙跳算法的分布式两阶段混合流水车间调度[J]. 控制与决策, 2021, 36(1): 241-248.

LEI De-ming, WANG Tian. An Improved Shuffled Frog Leaping Algorithm for the Distributed Two-Stage Hybrid Flow Shop Scheduling[J]. Control and Decision, 2021, 36(1): 241-248.

[5] 李燚, 唐倩, 刘联超, 等. 基于改进蚁群算法的汽车混流装配调度模型求解[J]. 中国机械工程, 2021, 32(9): 1126-1133.

LI Yi, TANG Qian, LIU Lian-chao, et al. An Improved ACO Algorithm for Automobile Mixed-Flow Assembly Scheduling Problems[J]. China Mechanical Engineering, 2021, 32(9): 1126-1133.

[6] 刘晨, 蒙丹花, 方玮宸, 等. 多品种小批量订单型企业生产调度优化[J]. 包装工程, 2016, 37(11): 93-99.

LIU Chen, MENG Dan-hua, FANG Wei-chen, et al. Production Scheduling Optimization of Enterprises with Multi-VARIETIES AND SMALL-BAtch Orders[J]. Packaging Engineering, 2016, 37(11): 93-99.

[7] 梁艳杰, 杨明顺, 高新勤, 等. 加工与装配车间集成调度的多目标优化模型[J]. 计算机工程与应用, 2016, 52(10): 247-253.

LIANG Yan-jie, YANG Ming-shun, GAO Xin-qin, et al. Multi-Objective Optimizing Model for Solving Mixed Model Shop of Fabrication and Assembly[J]. Computer Engineering and Applications, 2016, 52(10): 247-253.

[8] 郝琪, 张绪勇, 邢洁芳. 基于遗传算法的印刷企业生产调度模型的构建[J]. 制造业自动化, 2017, 39(1): 64-66.

HAO Qi, ZHANG Xu-yong, XING Jie-fang. Optimization of Scheduling of Printing Enterprises Based on Genetic Algorithm[J]. Manufacturing Automation, 2017, 39(1): 64-66.

[9] 雷斌, 刘同朝. 基于PSO-GA混合算法的转向架混流装配车间生产调度研究[J]. 现代制造工程, 2020(7): 19-24.

LEI Bin, LIU Tong-chao. Research on Production Scheduling of Bogie Mixed Flow Assembly Shop Based on PSO-GA Hybrid Algorithm[J]. Modern Manufacturing Engineering, 2020(7): 19-24.

[10] 龚鼎, 黄莺, 张永炬, 等. 基于能耗分析的轴类零件生产调度优化[J]. 轻工机械, 2017, 35(5): 91-95.

GONG Ding, HUANG Ying, ZHANG Yong-ju, et al. Production Scheduling Optimization of Shaft Machinery Parts Based on Energy Consumption Analysis[J]. Light Industry Machinery, 2017, 35(5): 91-95.

[11] 于蒙, 刘德汉. 改进PSO–GA算法求解混合流水车间调度问题[J]. 武汉理工大学学报(交通科学与工程版), 2021, 45(3): 586-590.

YU Meng, LIU De-han. Improved PSO-GA Algorithm for Hybrid Flow Shop Scheduling Problem[J]. Journal of Wuhan University of Technology (Transportation Science & Engineering), 2021, 45(3): 586-590.

[12] 孔琳, 王黎明, 李方义, 等. 基于机床加工匹配特性的混合流水车间绿色生产调度[J]. 计算机集成制造系统, 2019, 25(5): 1075-1085.

KONG Lin, WANG Li-ming, LI Fang-yi, et al. Sustainable Scheduling for Hybrid Flow-Shop Based on Performance Matching of Machine Tools[J]. Computer Integrated Manufacturing Systems, 2019, 25(5): 1075-1085.

[13] 宋存利. 求解混合流水车间调度的改进贪婪遗传算法[J]. 系统工程与电子技术, 2019, 41(5): 1079-1086.

SONG Cun-li. Improved Greedy Genetic Algorithm for Solving the Hybrid Flow-Shop Scheduling Problem[J]. Systems Engineering and Electronics, 2019, 41(5): 1079-1086.

[14] 陈金广, 马玲叶, 马丽丽. 求解作业车间调度问题的改进遗传算法[J]. 计算机系统应用, 2021, 30(5): 190-195.

CHEN Jin-guang, MA Ling-ye, MA Li-li. Improved Genetic Algorithm for Job Shop Scheduling Problem[J]. Computer Systems & Applications, 2021, 30(5): 190-195.

[15] 张超勇, 饶运清, 刘向军, 等. 基于POX交叉的遗传算法求解Job-Shop调度问题[J]. 中国机械工程, 2004(23): 2149-2153.

ZHANG Chao-yong, RAO Yun-qing, LIU Xiang-jun, et al. An Improved Genetic Algorithm for the Job Shop Scheduling Problem[J]. China Mechanical Engineering, 2004(23): 2149-2153.

Research on Production Scheduling Method of Guide Roll Based on Improved Genetic Algorithm

ZHANG Chao-yang1, XU Li-ping1, ZHANG Zeng-qiang2, LIU Shan-hui2, Li Jian1

(1. School of Mechatronics Engineering, Henan University of Science and Technology, Henan Luoyang 471000, China; 2.School of Printing, Packaging and Digital Media, Xi'an University of Technology, Xi'an 710000, China)

The work aims to study the scheduling optimization problem in the production workshop of guide roller, to shorten the completion time of workpiece and improve the production efficiency of the production line. A mathematical model was established with a guide roller production workshop as the research object to minimize the maximum completion time. In view of the actual working conditions of the guide roller production workshop, an improved genetic algorithm was proposed to solve the problems. Through the production scheduling of 10 guide rollers of different size, the improved genetic algorithm and the traditional genetic algorithm were used for experimental analysis. The results showed that the improved genetic algorithm had higher ability to find excellence than the traditional genetic algorithm, the completion time of the workpiece was shortened from 139 min to 113 min, by 18.7%. And the Gantt graph of production scheduling with a completion time of 113 min was generated. Compared with the traditional genetic algorithm, the improved genetic algorithm has higher global optimization ability and optimization accuracy in the optimization of guide roll production scheduling.

guide rollers; production scheduling; improved genetic algorithm; maximum completion time

TP391.2

A

1001-3563(2022)19-0208-08

10.19554/j.cnki.1001-3563.2022.19.024

2021–10–28

国家重点研发计划项目（2019YFB1707200）；陕西省技术创新引导专项（2020QFY03-08）

张朝阳（1994—），男，硕士生，主攻智能产线优化。

徐莉萍（1965—），女，硕士，副教授，主要研究方向为液压元件研究。

责任编辑：曾钰婵