基于LMS VirtualLab的刚性球散射计算

朱 菡

(中国船舶集团有限公司第七一三研究所,河南 郑州 450000)

数值仿真技术在现代工程中得到广泛应用,在声学仿真领域,球体的散射声场仿真具有严格的理论解析解,经常作为标准模型用于验证各种方法和理论,同时,由于球体本身可以作为某些特定问题的简化物理模型,常被作为简化模型进行实际问题的仿真计算。因此,球体的声散射仿真研究一直是人们关注的问题。本文首先对刚性球体散射声场远场理论解析解的推导过程进行了说明,并计算了刚球远场散射声压,其次采用直接边界元方法,应用Virtual.Lab软件对水下刚性球体散射声场进行仿真计算,并将计算结果与理论解析解进行比较,得到了令人满意的结果。

1 理论解析解

1.1 波动方程及其解

如图1所示,刚性不动球位于无限流体介质中,半径为,表面光滑,在沿轴方向传播的平面波(-)作用下,其散射声场声压在球坐标系中满足波动方程：

图1 平面波在球面上的散射

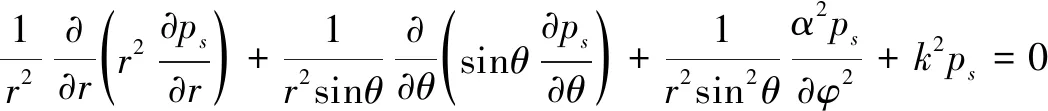
(1)

式中,、和为球坐标系中的坐标变量,=为波数,等于入射声波圆频率和球体周围介质中的声速之比。考虑球体的对称性,且入射波和散射波关于轴对称,因此,方程应与变量无关,式(1)简化为

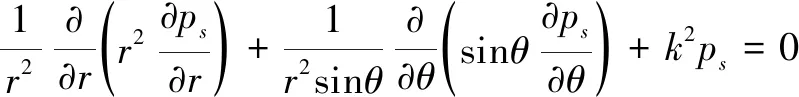
(2)

采用分离变量法求解上述方程可得

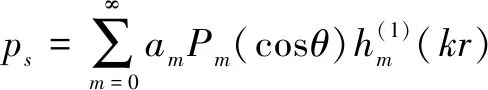
(3)

式中,为待定常数,由边界条件确定。

1.2 边界条件

刚性球体表面介质质点径向振速为零,即

(4)

式中,是球体周围介质中的密度,是介质中的总声压,即入射声压和散射声压之和,是介质质点振速的径向分量,即入射波引起的介质质点振速的径向分量和散射波引起的介质质点振速的径向分量之和。

用勒让德函数(Legendre Function)和球贝塞尔函数(Spherical Bessel Function)表示入射波,并利用关系式:

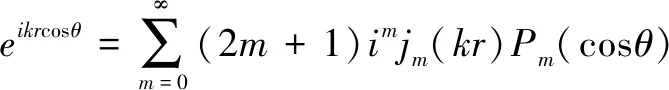
(5)

可求得常数为

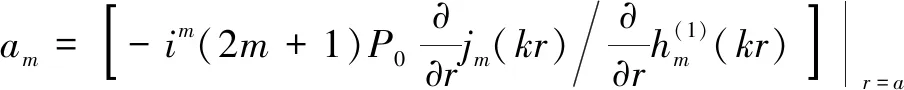
(6)

式中，()为阶球贝塞尔函数。

1.3 散射声场的远场解

将式(6)代入式(3)并加入时间因子-得到散射声表达式为

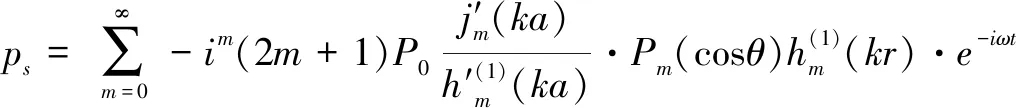
(7)

式(7)是散射声场的一般表达式,但人们一般更关心它的远场特性,因此,可用球汉克尔函数(Spherical Hankel Function)在大宗量条件下的渐近展开式:

(8)

代入式(7)得

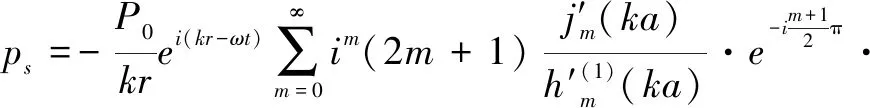
(9)

若记

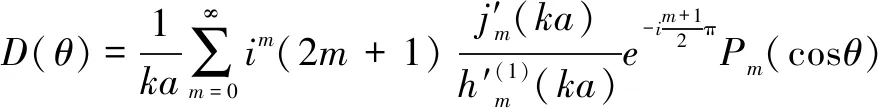
(10)

则式(9)转化为

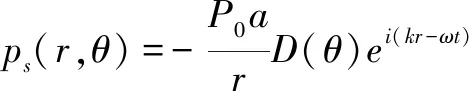
(11)

1.4 解析解计算

上文中提到的指向性函数()是用于描述刚球散射声场的一个重要参量,因此,为计算刚球的指向性函数,计算模型选取半径为1 m的刚性不动球,入射声波选取单位波幅平面波,取计算阶数=100,无因次系数={1,2,3,4,5,6,7,8},声速=1 500 m/s,为满足远场条件,需要计算获得距刚球之外的声压,其中,为刚球尺度,为声波波长,因此,计算=50 m处的散射声压,并利用球面衰减规律归算到刚球等效声中心1 m处,如图2所示。

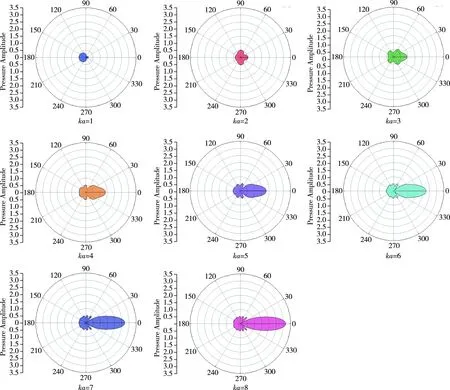
图2 不同ka值下的刚球指向性图

2 边界元方法

2.1 Helmholtz积分方程

刚球声散射计算属于外部问题,即所要计算的声场变量都在刚球封闭表面外部,满足Helmholtz方程:

(12)

式中,为声压,为三维自由空间格林函数:

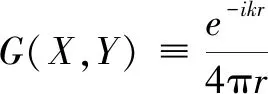
(13)

如图3所示,刚球表面为,在体积为表面为Σ半径无限大的区域内,除点为格林函数的奇异点外,其余各点的声压在这个空间内是平稳和非奇异的,因此,可环绕点做半径→0的表面为的小球,在表面积为++Σ的空间-内就不再有奇异性。

图3 计算区域定义

将式(12)代入格林公式,则有

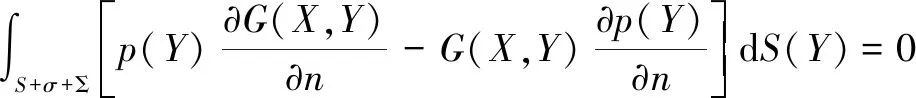
(14)

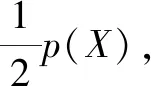
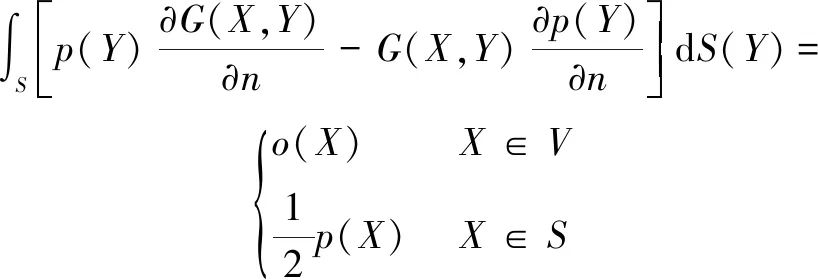
(15)

式中,表示球体外部空间,表示球体表面。

2.2 边界元方法

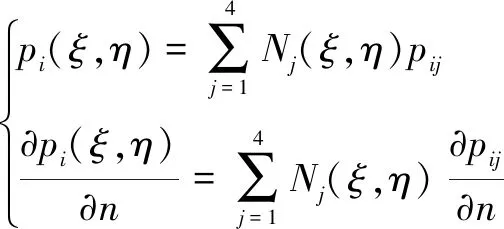
(16)

式中,(,)为单元形函数,当单元为四节点四边形时,有

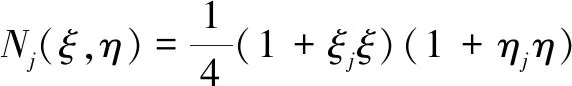
(=1,2,3,4)

(17)

式中,和为单元第个顶点的局部坐标,其值为

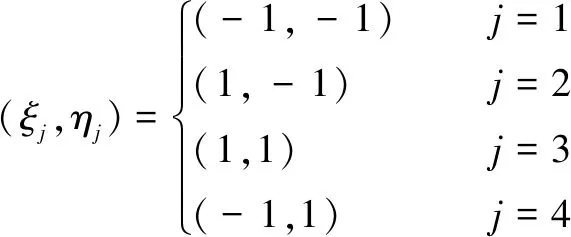
(18)

将式(16)、(17)代入离散后的式(15),经整理得

(19)

式中,[]和[]为系数矩阵,若表示球面声压,则式(19)给出了声压及其法向导数的关系,通过求解该微分方程组即可得到刚球表面声压分布,进而得到空间内任意一点的散射声压值。

2.3 Virtual.Lab Acoustics声学仿真计算

平面波作用下,刚球散射声场可以采用Virtual.Lab Acoustics声学模块进行仿真计算,本文建立刚球四边形边界元网格,如图4所示,网格划分尺寸通常取波长的1/6,即

图4 边界元网格

(20)

式中,为网格最大尺寸,为声波波长,为频率,为水中声速。

分别计算={1，2，3，4，5，6，7，8}时的散射声场,图5给出了刚球周围2 m范围内近场的声压干涉图。

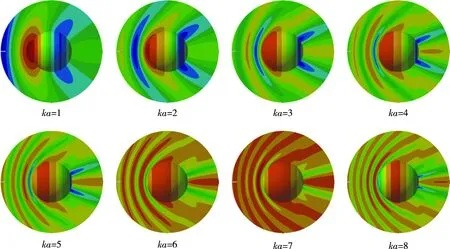
图5 刚球声散射近场声压干涉图

可以看出,边界元算法能够对刚性球表面声压和球体周围声场分布给出较好的计算结果,不论球体的声学“照亮区”还是“影区”,算法均能给出准确的计算结果,同时,随着ka值即计算频率的增大,刚性球近场声压干涉条纹随之加密,能够较好地模拟水下目标近场声压分布。

为了与上文中的理论解析解进行比较,本文需要计算刚球指向性函数,为此利用软件自带的Field Point Meshes功能下的Directivity Field Point Mesh功能,在距球心50 m处每隔1°设置一个计算场点,用于提取该处的声压。将提取到的声压根据球面衰减规律归算到刚球等效声中心1 m处,并与解析解进行比较,如图6所示。可以看出,数值算法的计算结果与理论解析解吻合较好,能够准确地给出刚性球不同ka值下的指向性,证明该方法能够准确模拟任意分置角下水下目标收发分置声散射强度。

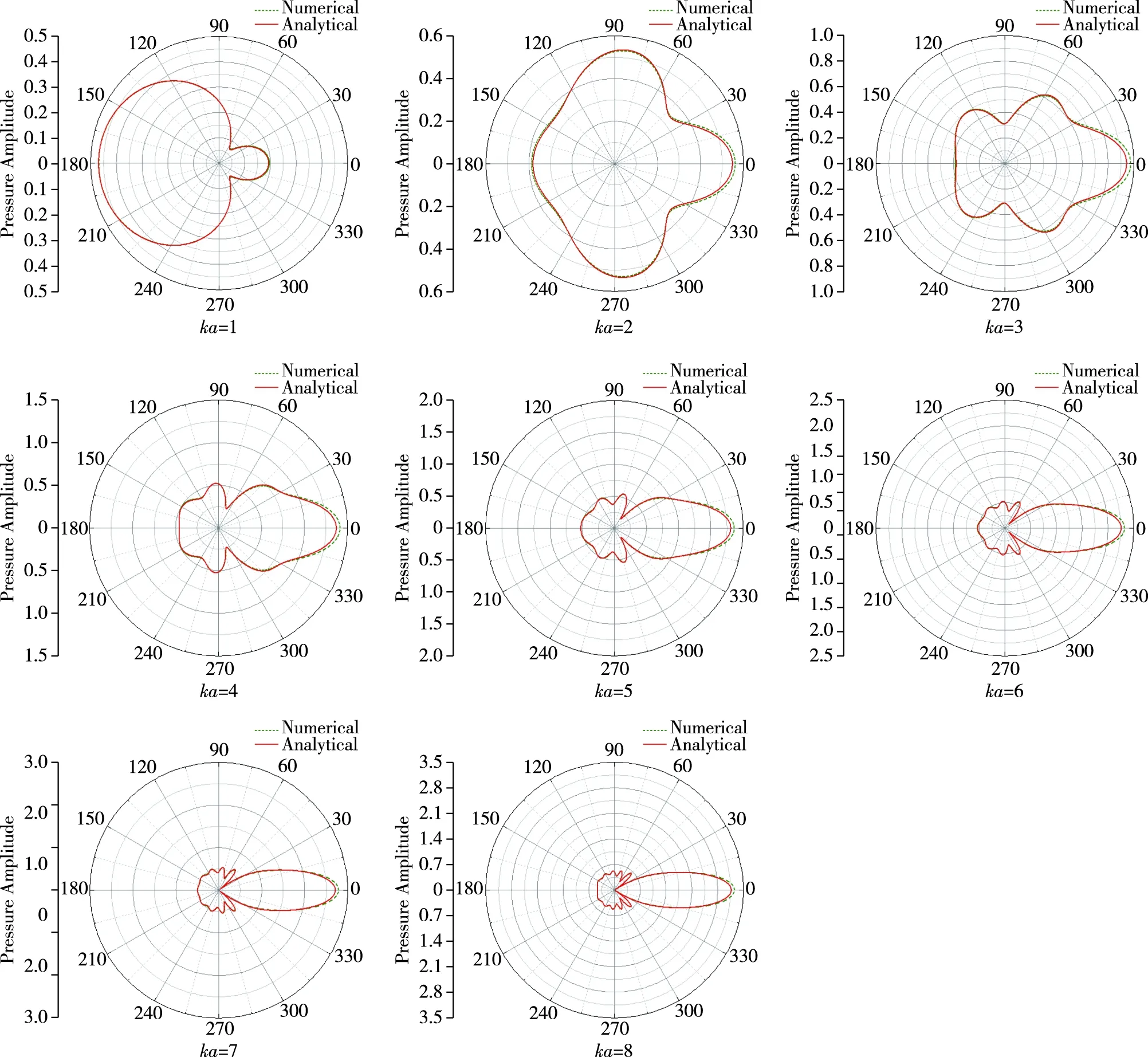
图6 远场声压指向性数值解与解析解比较

3 结束语

本文利用LMS Virtual.Lab软件,采用直接边界元法计算水下刚性球体在平面声波作用下的指向性函数,并与理论解析解进行比较,得到如下结论:

1)无论解析解还是边界元方法数值解,计算时需满足远场条件,否则,无法得到稳定的、吻合度较高的计算结果;

2)采用Virtual.Lab Acoustics声学模块计算远场声压时,当计算点输出声压数值较小时,需要提高软件参数设置中默认声压输出精度,否则,导出的计算结果数据精度将无法满足需要;

3)边界元法能够准确计算水下目标的表面声压分布、近场声场分布以及收发分置声散射强度,可用于水下目标声散射特性预报。