基于贪婪策略的紧密k 核子图查询
2022-10-16赵丹枫姚贤标包晓光黄冬梅郭伟其
赵丹枫,姚贤标,包晓光,黄冬梅,郭伟其
(1.上海海洋大学 信息学院,上海 201306;2.上海电力大学 电子与信息工程学院,上海 200090;3.国家海洋局 东海海洋环境调查勘察中心,上海 200137)
0 概述
图查询是图数据分析与处理的基础,其中社团检测作为一种子图查询,其目标是从给定的图中寻找所有紧密连接的子图,并且各个图内部的节点是连通的[1]。紧密子图查询作为社团检测的核心,在很多领域都有着重要的应用,例如:在社交网络中,查询联系紧密的社团有助于用户的特征分析[2];在作者的合作网络中,联系紧密的作者之间可能具有相似的研究领域[3];在商品销售数据中,联系紧密的商品更有可能被相似的消费者所关注[4];在蛋白质网络中,关系紧密的蛋白质通常更有可能形成特定的官能团[5]。
在现有的研究中,研究人员提出许多社团检测方法,如基于模块度优化的算法[6]、谱方法[7]、非负矩阵分解[8]等。对于社团的定义也有多种,常见的有k架(k-truss)、k团(k-clique)、k核(k-core)等,其中k核的定义[9]要求图中每个节点至少有k个邻接节点,即每个节点的度至少为k。k核可以在线性时间复杂度内计算得到,具有较好的应用基础[10-12]。近年来的研究多结合部分场景的应用需求,讨论各类属性图上的k核子图查询[13-15]。然而,由于考虑边权值的研究较少,但在很多场景下,图中边的权值往往具有很强的语义关系。例如在社交网络中,两个用户之间的交流越频繁意味两者之间的联系越紧密。在作者的合作网络中,若两个作者之间合作的次数越多,则说明他们的联系越紧密,对应图中边的权值越大。因此,为了使社团检测更加符合实际的语义场景,提高查询结果的合理性,则需要将图中边的权值考虑在内。
此外,考虑到查询最紧密社团往往会耗费较多的时间,并且在一些应用场景下不需要查询社团权重的最值,例如在蛋白质网络中,有时仅需要找到满足一定紧密关系的蛋白质集合即可。为此,不局限于社团检测中最值的查询,给定核值k、节点平均权值wQ,在加权图中查询联系紧密的连通k核子图问题,记为紧密k核子图查询(Closely Relatedk-Core Subgraph Query,CRKSQ)问题。该问题要求查询得到的连通k核子图的节点平均权值大于等于wQ,其进一步限制了子图的紧密程度,且由于wQ可以根据实际需求给出,具有更好的灵活性,更加切合实际应用场景。
为解决CRKSQ 问题,本文首先证明该问题是一个NP-难问题,即无法为其找到一个在多项式时间复杂度内的最优算法,并基于贪婪策略设计启发式算法CRK-G。在此基础上,研究CRK-G 算法的优化策略,提出CRK-C 和CRK-F 算法,分别从降低图规模和减少迭代次数两个方面提高查询效率。最后通过实验对比3 种算法在不同场景下的效率。
1 相关工作
目前针对社团的查询已经有了广泛的研究,除k核外,主要还包括基于k-truss和k-clique 的查询问题。k-truss和k-clique 相对于k核有着更加严格的定义,但都与k核类似,其本身并未考虑图中的其他属性,仅仅只是从图中寻找稠密且内聚的结构。近年来的很多研究也开始结合图的语义关系,探索更加高质量的k-truss和k-clique 社团[16-18]。
与上述两种社团的定义相比,k核可以被有效地在线性时间内计算,其概念最初由SEIDMAN[9]在1983 年提出。为了高效地进行k核的查询,BATAGELJ等[19]于2003 年提出了k核分解算法,其能在O(m)时间复杂度下得到每个节点的最大核值,进而能够在线性时间内得到k核查询的结果。文献[20]为应对大图的查询,又提出了效率更高且能在个人计算机上运行的3种k核分解算法,其查询速度有了很大的提升。为提升k核查询的效率,文献[21]提出了面向k核查询的图压缩算法SC,进一步将压缩图转化为树的算法TC,其算法效率比可以比直接在原图上查询的效率高出1~2 个数量级。
为了优化k核社团查询,文献[22]提出一种能够支持多个节点查询的社团搜索问题,解决了以往单节点查询带来的通用性的不足。文献[23]考虑到现有的社团查询方法使用的都是全局搜索,算法代价较高,故提出一种局部搜索方法。上述两种方法虽然在查询条件上做了优化,但却都未结合图上的其他属性,仅面向简单图的查询。
近年来,研究人员开始致力于寻找更加紧密的k核子图,文献[13]结合图中节点的影响力,提出了k-influential 社团模型,用于在大图中查询最具影响的社团。文献[14]考虑边的有向性,研究了有向图上的社团搜索问题,其利用最小内度和外度的度量方法寻找紧密连接的子图。文献[15]研究了轮廓图的社团搜索(PCS)问题,其能够识别具有语义共性的节点,从而发现更多高质量的社团。上述研究结合了图上的其他属性,在相应的场景下能得到更加合理有效的社团,而对于边权值属性的社团查询方面,目前的研究还不充分。虽然文献[24]提出了查询加权图的亲密核心组问题,但由于其模型属于社团搜索,仅针对给定节点集的查询,并且是查询总权值最小的子图,与部分应用场景不符,具有一定的局限性。
本文考虑了节点的语义关系,不局限于社团检测中最值的查询,提出了在加权图中查询联系紧密的连通k核子图问题,以实现更好的灵活性,且更贴合实际应用场景。
2 定义与证明
2.1 紧密k 核子图的定义
本文研究的是无向加权图上的子图查询,该研究是在k核的基础上进行的,故先给出k核的定义。
定义1(k核)[9]给定图G=(V,E),k核是图G的极大子图H,使得H中的每个节点至少有k个邻节点。
定义2(核值)给定图G=(V,E),对于G中的节点u,u∈V,u的核值core(u)为u所在全部k核中的最大值,即:

例如,在图1 中,节点集{a,b,c,d,f}和{o,p,r,s}的导出子图中节点核值都为3。但需要注意的是,节点的核值并不等于节点的度,如图1 中的节点c,其节点的度为4,但核值却为3。此外,k核并不一定是一个连通的图,如图1(b)表示的是图1(a)中加权图G的3 核子图,该图并不是连通的。

图1 k 核查询实例Fig.1 Example of k-core query
定义3(连通k核)给定图G=(V,E),连通k核是图G的极大连通子图H,使得H中的每个节点至少有k个邻节点。
连通k核是在k核的基础上定义的,其表示的子图一定是一个连通的图。本文研究的是连通k核,若不加特别说明,下文中提到的k核均表示的是连通k核。
定义4(节点权值ω)给定一个加权图G=(V,E,W),对于G中的节点u,u∈V,节点u的权值为与其相连边的权值之和,即节点权值:

例如,在图1 中,与节点a相连的边有3 条,各边权值分别为7、8、10,故其节点的权值ω(a)=7+8+10=25。
定义5(节点平均权值Aw)给定一个加权图G=(V,E,W),图G节点平均权值为每个节点的权值之和除以图G的节点数,即图G节点平均权值为:

节点平均权值反映的是整个子图内部的紧密程度,节点平均权值越大则说明子图内部节点之间的交互越多,子图就越紧密。
下面给出紧密k核子图(Closely Relatedk-Core Subgraph)的定义。
定义6(紧密k核子图)给定一个加权图G=(V,E,W),核值k,节点平均权值wQ,紧密k核子图H=(V',E',W),H满足以下条件:1)H⊆G;2)H是连通k核;3)图H的节点平均权值Aw(H)≥wQ。
紧密k核子图的定义在k核的基础上进一步限制了子图的节点平均权值,该限制将会消除图中权值较小的节点,使得图整体的紧密性有所提高。
紧密连接k核子图查询如图2 所示,其中图2(b)为加权图G(见图1(a))在给定k=2、wQ=20 时得到的紧密2 核子图H。图H的每个节点都至少有2 个邻节点,且图的节点平均权值为21.6,满足给定条件。对比图2(a)和图2(b),可以看出后者节点之间的联系更加紧密,整体也更加紧凑。

图2 紧密连通k 核子图的查询实例Fig.2 Example of closely related connected k-core subgraph query
定义7(紧密k核子图查询)给定一个加权图G=(V,E,W),核值k,节点平均权值wQ,在图G中寻找紧密k核子图H。
紧密k核子图查询(CRKSQ)问题的目的是在图中找到满足条件的紧密k核子图。需要注意的是,紧密k核子图在图中不一定只有一个,有可能存在多个。
2.2 QCRKS 问题的证明
引理1给定一个加权图G=(V,E,W),图G中节点权值之和等于图G中各边权值之和的两倍,即:

证明由于图G中的每条边连接两个节点,而根据节点权值的定义可知图中每条边的权值会被相连的两个节点各计算一次,故上述结论成立。
定理1CRKSQ 问题是NP-难的。
证明将clique 问题多项式归约到CRKSQ 问题。由于clique 问题是一个NP-完全问题[25],进而得出CRKSQ 问题是NP-难的。给定clique 问题的一个实例I,其由一个无权图G=(V,E)和一个正整数k构成。构造CRKSQ 问题的一个实例I':一个加权图G'=(V,E,W),这里每条边权值都为1;另一个正数wQ=k-1。显然,这是一个多项式归约。下面只需证明实例I存在一个k阶完全子图,当且仅当,实例I'存在一个节点平均权值大于等于wQ(wQ=k-1)的紧密(k-1)核子图。
假设clique 问题存在一个k阶完全子图H。现证明H作为G'的子图,其是一个满足条件的紧密(k-1)核子图。由完全子图的定义可知,H中的每个节点具有(k-1)个邻接节点,且平均权值为:

根据引理1,式(5)可化为:
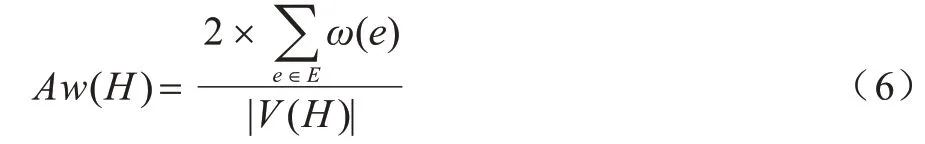
因G'中每条的权值都为1,故:

得证。
反之,假设G'中存在一个满足条件的紧密(k-1)核子图H。由子图H是一个(k-1)核知,H具有至少k个节点;由节点平均权值大于等于wQ(wQ=k-1),并由引理1 可知,H具有k(k-1)条边,因此作为G'的子图H是一个k阶完全子图。得证。
3 基于贪婪策略的查询算法
由定理1 可知,无法为CRKSQ 问题找到一个多项式时间复杂度的最优算法,为解决该问题并在可接受的时间内找到合适的解,本文基于贪婪策略提出了启发式算法CRK-G。首先从图中找到候选k核子图,然后通过不断地迭代删除候选子图中权值最小的节点,进而得到满足条件的紧密k核子图。
3.1 CRK-G 算法
CRK-G 算法步骤如下:
步骤1使用k核分解算法[20]计算每个节点的核值。
步骤2使用广度优先搜索,得到候选k核子图集合。
步骤3判断子图节点平均权值是否小于wQ,若小于则迭代删除图中权值最小的节点。
步骤4为了保证剩余子图的k核连通性,还需要删除图中节点度小于k的节点,随后判断子图是否连通,若不连通则将每个独立的连通子图分隔,并加入候选子图集合等待后续的处理。
步骤5重复上述操作,直到剩余子图的节点平均权值大于等于wQ,或节点被全部迭代删除为止。算法最后返回满足条件的紧密k核子图集。
例如,在图2 中,给定图G(见图1(a)),核值k=2,节点平均权值wQ=20。算法首先查询得到候选2 核子图H',随后开始判断子图H'的节点平均权值是否大于等于wQ,经计算可知节点平均权值小于20。因此,开始删除最小权值的节点e。删除节点e后,节点平均权值仍然小于20,则再依次删除节点s、节点r。其中,删除节点s和节点r导致节点p的度小于2,则再将节点p删除,此时剩余子图仍然是连通的。重复上述步骤再依次删除节点o、节点h,最终得到图2(b)中满足条件的紧密2 核子图H。
算法1紧密k核子图查询算法CRK-G

3.2 CRK-G 算法的复杂度分析
CRK-G 算法采用贪婪思想,通过迭代删除节点而使得子图满足条件,其主要时间花费包括k核候选子图查询、节点平均权值计算、子图连通性判断以及子图k核的维护。首先,在k核候选子图的查询方面,使用的是广度优先搜索算法,其时间复杂度为O(|V|+|E|)。其次,在节点平均权值计算和子图连通性判断方面,计算节点平均权值需要耗时O(|E|),寻找最小权值的节点需要耗时O(|V|),若算法需要迭代t次,则计算节点平均权值耗时O(t(|V|+|E|))。连通性判断使用的是广度优先搜索,耗时也为O(t(|V|+|E|))。最后,在子图k核的维护方面,查询节点的度耗时为O(|E|),若算法需要迭代t次,则这一步总耗时为O(t(|E|))。最终CRK-G 算法的时间复杂度为O(t(n+m)),其中n和m分别表示原图的节点数和边数。
下文分析CRK-G 算法的空间复杂度,对于原图中的每个节点,需要存储其邻节点以及其与邻节点之间边的权值,所以空间消耗为O(2|E|)。另外,还需要存储候选子图中节点的邻节点以及节点与邻节点之间边的权值,空间消耗为O(2|E|)。总共空间消耗为O(4|E|),故CRK-G 算法的空间复杂度为O(m)。
4 CRK-G 算法的优化
CRK-G 算法对于CRKSQ 问题的求解是有效的,它能在O(t(n+m))时间内找到一个解,但对于在大规模图上的查询而言,该算法求解需要花费大量的时间,效率较低。
根据对CRK-G 算法时间复杂度的分析,影响其效率的主要因素是图的规模和迭代的次数,因此可以通过使用降低图规模或减少迭代次数的方法,使得算法的效率提高。基于该思路,本节提出了CRK-G 算法的两种改进算法:1)使用图压缩策略的CRK-C 算法,其适用于节点权值差异性较小的图数据;2)使用单次多节点删除策略的CRK-F 算法,该算法实现简单,效率提高明显,适用于差异性较大或无法确定差异性的图数据。
4.1 基于图压缩的优化策略
目前关于面向特定查询的图压缩已经有了广泛的研究,常见的如面向保持可达查询的图压缩[26]、面向邻节点查询的压缩[27]以及面向k核查询的图压缩[21]。与大部分面向特定查询的压缩技术类似,本文的压缩方法遵循查询等价原则,通过将权值相近的节点合并得到超节点,判断超节点所包含的节点在原图中是否存在边来构建超边以及超边的权值。
定义8(超节点和超边)给定图G=(V,E),其经过压缩后得到GC=(V',E'),其中,由原图节点集V分割得到,即⊂V(i=1,2,…,n),并且,则节点v'∈V'被称为超节点,边e'∈E′被称为超边。
例如,图3(b)的图H'C表示的是一个压缩图,其每个节点表示的即为超节点,如超节点s1包含了原图H'中的节点a、节点c和节点d。压缩图中的边即为超边。
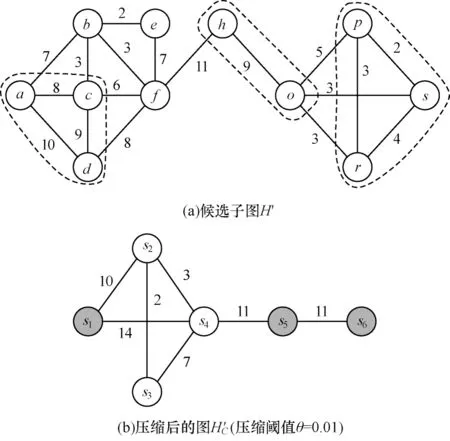
图3 图压缩实例Fig.3 Example of graph compression
定义9(压缩比cr)给定图G=(V,E),其经过压缩得到GC=(V',E'),则压缩比为:

压缩比是衡量图压缩是否有效的重要指标,根据压缩比的定义可知,压缩比越小,则压缩后的图规模也越小。
4.1.1 CRK-C 算法
CRK-C 算法在CRK-G 算法的基础上进行,查询到候选k核子图集后,对每个候选子图进行压缩,得到压缩后的图GC,在后续的迭代删除过程中直接对GC进行操作。压缩算法步骤如下:
步骤1遍历图中的所有节点,将权值相近的节点合并,从而得到超节点。
步骤2超节点包含的节点若在原图中存在边,则在超节点之间构建超边。
步骤3超边的权值设为两个超节点所包含的原节点在原图中边权值之和。
其中,步骤1 的节点合并是通过设置压缩阈值θ(θ∈(0,1)),根据起始节点的权值ω,将节点权值在±θω之间的连通节点进行合并。
例如,图3(a)表示的是一个2核候选子图,节点a、节点c和节点d的权值分别为ω(a)=25、ω(c)=26、ω(d)=27,节点之间的最大差值为2,当压缩阈值θ=0.01 时,最大允许的权值差值为2.5(θω(a)=2.5),所以节点a、节点c和节点d可以被压缩为一个超节点s1。由于图H'中节点a、节点c与节点b存在边,而节点b压缩后由超节点s2表示,因此超节点s1和超节点s2之间存在边,边的权值为原图中边(a,b)和边(c,b)的权值之和,即7+3=10。重复上述压缩步骤,最终该候选子图H'经过压缩得到了图H'C,压缩后图的规模与原图H'对比明显有所降低,压缩比cr=
7/18≈0.39。
压缩算法GC-W 见算法2,算法最后返回压缩后的图GC和映射表M,M中记录了原图G中每个节点所对应的超节点。借助M,可以在O(n)时间内将压缩后的图解压缩,n表示的是原图的节点数。
需要注意的是,压缩阈值θ越大,算法查询速度越快,但对应着查询结果的误差也会增大。根据算法特点,压缩阈值θ的取值误差主要取决于候选子图节点权值的波动或偏移程度,故可以使用子图中节点权值的差异系数(Coefficient of Variation,CV)作为θ的取值依据,其反映了子图节点权值的离散程度,计算公式为:

其中:σw为子图权值的标准差;Aw为子图平均节点权值。
算法2压缩算法GC-W

4.1.2 CRK-C 算法的复杂度分析
CRK-C 算法在原有贪婪策略的基础上新增了图压缩的步骤,其主要的时间花费包括k核候选子图查询、图压缩、节点平均权值计算、子图连通性判断、子图k核维护以及最后压缩图的解压缩。
1)在k核候选子图查询方面,其时间复杂度与CRK-G 算法一致,都为O(|V|+|E|)。
2)在图压缩方面,其主要由超节点划分和创建超边两部分组成。其中超节点划分是通过广度优先搜索算法,不断地扩展与节点u权值相近的节点,直至无法扩展为止,该步可以在O(|V|+|E|)时间内完成;而超边的创建是通过依次访问原图G中的每一条边,从而确定压缩图的边集,则其时间复杂度为O(|E|)。因此,整个图压缩算法GC-W 的耗时为O(|V|+2|E|)。
3)在节点平均权值计算和子图连通性判断方面,假设图压缩的压缩比为cr,则压缩后节点和边的数量大致可以表示为(cr)|V|和(cr)|E|。此外,由于节点和边的数量减少,算法迭代的次数也会相应减少。若压缩前需要的迭代次数为t,则压缩后需要的迭代次数大致为(cr)t。因此,节点平均权值的计算需要耗时O(t(|V|+|E|)(cr)2)。子图连通性判断使用的是广度优先搜索,所以耗时也为O(t(|V|+|E|)(cr)2)。
4)在子图k核的维护方面,由于压缩图没有保留原节点的度信息,因此查询节点度的耗时没有变,仍然为O(|E|),算法需要迭代(cr)t次,则此步的总耗时为O(t(cr)|E|)。
5)在压缩图的解压缩方面,由于压缩算法GCW 会返回一个映射表M,M中记录了原图G中每个节点所对应的超节点。借助M,可以在O(|V|)时间内将压缩后的图解压缩。
最终CRK-C 算法的时间复杂度为O(t(cr)m),其中,t表示迭代次数,cr表示压缩比,m表示原图的边数。
接下来分析CRK-C 算法的空间复杂度,由于该算法在CRK-G 算法的基础上引入了图压缩过程,因此在计算过程中除了原有的空间消耗外,还需要额外存储压缩图的信息,压缩图信息包括每个超节点的邻节点和超边的权值,假设图压缩的压缩比为cr,则其空间消耗为O(2(cr)|E|)。原有的空间消耗为O(4|E|),故CRK-C 算法的空间复杂度为O(m)。
4.1.3 CRK-C 算法的误差分析
CRK-C 算法虽然提高了效率,但是其相对于CRK-G 算法存在一定的误差。CRK-C 算法可能导致的误差是其多迭代删除的节点数。假设经过压缩算法压缩后的压缩比为cr,在压缩图中平均一个节点对应原图1/cr个节点。在最坏的情况下,某次迭代删除中正常迭代删除一个节点即可达到紧密k核子图的要求,而由于采用的是压缩图进行迭代,则该次删除的节点数为1/cr,误差为(1/cr)-1 <1/cr,即CRK-C 算法的平均误差小于1/cr,压缩比cr越大则误差越小。
需要说明的是,压缩比cr取决于压缩阈值θ的取值,θ和cr的具体关系则还要结合候选子图中节点权值的情况。但若在同一个图数据中,θ越大则会有更多的节点被合并,伴随着压缩比cr会越小。
4.2 基于单次多节点删除的优化策略
提高CRK-G 算法效率的改进策略除降低图规模外,另一种方法是减少算法的迭代次数,而减少迭代次数的一个有效且直接的方法是批量删除节点。通过在单次迭代中一次性删除多个节点来减少迭代次数,从而提高算法的效率。
4.2.1 CRK-F 算法
基于单次多节点删除策略,对CRK-G 算法进行改进,得到效率更高的快速贪婪算法CRK-F。CRKF 算法设置了每次迭代时的删除比率γ,其中γ∈(0,1)。若候选子图H的节点数为|V()H|,设迭代时删除的节点集为S,则节点集S的数量|S|=γ|V(H)|。节点集S的取值是通过对每次迭代后剩余子图的节点按节点权值进行排序,权值最小的前γ|V(H)|个节点组成的集合即为节点集S。在下一次迭代删除时,S即作为需要从候选子图中删除的节点集。
需要说明的是,γ越大则每次迭代删除的节点数就越多,总的迭代次数就越少,可能导致的误差就越大。γ的参考取值可经过计算得到,假设迭代删除一个节点后,子图的节点权值平均上升Δ-----Aw,则:
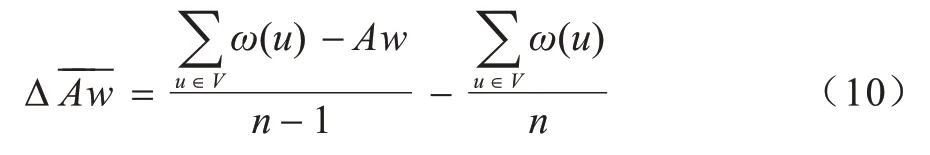
目标节点平均权值wQ和当前候选子图的节点平均权值Aw之间的差值ΔwQ=wQ-Aw,假设需要删除K个节点后子图节点平均权值为wQ,则:

而迭代删除的节点数K=γ|V|,则:

在实际应用时,式(12)可作为γ的取值依据。一般来讲,取值时考虑目标节点平均权值wQ和当前候选子图的节点平均权值Aw之间的差值。当差值较大时,γ取值可适当增大,使其能更快地迭代到目标值附近;反之,γ取值可适当减小。
4.2.2 CRK-F 算法的复杂度分析
CRK-F 算法克服了CRK-G 算法效率低下的问题,通过利用单次多节点删除的方法,极大地减少了算法的迭代次数,接下来对该算法进行时间复杂度与空间复杂度分析。
CRK-F 算法与CRK-G 算法相比,前者的迭代次数减少。首先分析改进后算法的迭代次数,初始时候选子图H的节点数为|V(H)|≤|V(G)|,其中G为给定需要查询的原图。若每次迭代删除的节点集为S,则经过i次迭代后,|S|=γ|V(Hi)|,即此时节点集S将从剩余子图Hi中删除。这表明在经过第i+1 次迭代后,剩余子图Hi+1中至多有(1-γ)(|V(Hi)|)个节点,即假设需要进行t'次迭代后算法才结束,则:

CRK-F 算法与CRK-G 算法在空间上的消耗没有区别,所以CRK-F 算法的空间复杂度也是O(m)。
4.2.3 CRK-F 算法的误差分析
根据CRK-F 算法特点可知,其相对于CRK-G 算法的误差是由于批量删除时多删除的节点导致。
假设给定删除比率γ,当算法迭代到第t次时结束,那么在t-1 次时候选子图剩余的节点数为(1-γ)t-1(|V|)。随后进行第t次迭代,在最坏情况下,本次迭代原本只需要删除一个节点即可达到紧密k核子图的要求,而由于采用批量删除,实际删除的节点数为(1-γ)t-1(|V|)γ,误差为(1-γ)t-1(|V|)γ-1 <(1-γt-1(|V|)γ,即CRK-F 算法误差不超过(1-γ)t-1(|V|)γ。
4.3 CRK-C 与CRK-F 算法对比分析
通过对CRK-C 与CRK-F 算法的原理分析,对两者的特点总结如下:
1)CRK-C 算法使用了图压缩策略,通过将节点权值在阈值范围内的连通节点进行合并,从而降低子图的规模,也相应减少了迭代次数,算法效率相对CRK-G 算法而言有了较大的提升。根据算法的特点,若图中节点权值较为相近时,节点压缩策略将会起较大的作用。在节点压缩时,更多节点权值相近的节点将会被合并,并且由于被合并的节点权值相近,其在迭代删除过程中所造成的误差也较小,因此CRK-C 算法更适用于图中节点权值差异性较小的数据。
2)CRK-F 算法利用单次多节点删除策略,每次迭代删除多个节点,显著减少了迭代次数。由于CRK-F 算法仅需要在迭代删除时设置删除比率γ,从而进行节点的批量删除,其实现相较于CRK-C 算法而言更加简单,效率提升也较为明显。并且根据算法的特点,其误差能够较好地被预测,有利于控制算法的误差。当图中节点权值差异性较大或无法确定差异性时,可优先考虑使用CRK-F 算法。
5 实验结果与分析
本文在3 个真实数据集上进行了实验,对比了算法在不同查询条件下和不同规模图上查询的耗时,并分析压缩算法GC-W 和紧密k核子图模型的有效性,最后结合实例进一步说明模型的优越性。
5.1 数据集
本文实验使用的数据集主要有以下3 个:
1)生物通用交互数据集Bio-GRID,其中节点表示基因或蛋白质,边表示基因或蛋白质之间存在交互,边的权值表示节点之间交互的得分,得分越高说明节点之间的联系越紧密。
2)美国安然公司的邮件网络Email-Enron,其中顶点表示邮箱,边表示一个邮箱向另一邮箱发送过邮件,边的权值表示邮箱之间邮件的互通次数,次数越高说明邮箱之间的联系越紧密。
3)由DBLP 数据构成的作者协作网络,其中节点表示作者,边表示两个作者共同合作发表过文章,边的权值表示作者合作过的次数,次数越高说明作者之间的联系越紧密。
上述数据集经预处理转化为图数据,各个图的基本特性如表1 所示。其中:节点数和边数反映了图的规模;最大核值为k核分解后图中节点最大的核值,反映了图中最稠密社团的稠密度;平均核值反映了图整体的稠密程度;节点平均权值反映了图节点之间整体联系的紧密程度。

表1 数据集的基本特性Table 1 Basic characteristics of dataset
5.2 实验分析
本文在上述3 个数据集上进行实验,对比了算法CRK-G、CRK-C、CRK-F 在不同条件下的查询效率和图压缩算法GC-W 的压缩效率,并验证了模型的有效性。实验使用C++实现,在2.90 GHz IntelⓐCoreTMi5-9400 CPU、8.0 GB 内存、Windows10 系统的台式机上运行。
5.2.1 算法效率分析
在查询紧密k核子图时,需要给定核值k和节点平均权值wQ。为验证算法的效率,本文设计了控制变量的对比实验,记录3 个算法随着给定值变化时其查询所消耗的时间。在下文实验中,CRK-C 算法的压缩阈值θ=0.01,CRK-F 算法的删除比率γ=0.1。
由于查询参数的取值不是本文的研究重点,实验中的参数值是通过前期的初步实验并结合数据集的特性得到。其中,参数wQ的给定是通过初步的实验,大致计算得到各个数据集子图的最大节点平均权值,将该值取整十或整百,然后等差递减得到wQ的取值范围。在实际应用中可以根据对子图紧密程度的需求来选择核值k和节点平均权值wQ,以及对误差允许的范围来选择合适的压缩阈值θ和删除比率γ。
本文分别控制k和wQ的变化,在3 个数据集上进行以下两组实验:
1)随着给定节点平均权值wQ的变化,实验并记录在3 个数据集上算法CRK-G、CRK-C、CRK-F 查询所需要的时间。对于数据集Bio-GRID,给定k=20,变量wQ的取值范围为{20,30,40,50,60};对于数据集Email-Enron,给定k=30,变量wQ的取值范围为{9 000,10 000,11 000,12 000,13 000};对于数据集DBLP,给定k=40,变量wQ的取值范围为{200,225,250,275,300}。
3 种算法随wQ变化的运行效率对比结果如图4所示,随着节点平均权值wQ增大,各算法在不同数据集上的查询耗时总体均增加。之所以如此,是因为当给定节点平均权值wQ增大时,算法所需要的迭代次数增多,故耗时增加。在3 种算法的效率对比中,CRK-G 算法的查询耗时明显高于另两种算法。在Bio-GRID 数据集上,CRK-C 算法的速度略快于CRK-F 算法,通过对数据集特性的分析,发现Bio-GRID 数据集中存在较多权值相近的节点,使得该数据集的候选子图经过压缩后的压缩比较低,故CRKC 算法的查询速度较快。反之,在DBLP 数据集上,CRK-F 算法速度快于CRK-C 算法是由于该数据集上权值相近的节点较少。

图4 3 种算法随wQ 变化的运行效率对比Fig.4 Comparison of the operating efficiency of the three algorithms with the change of wQ
2)随着给定核值k的变化,实验并记录在3 个数据集上算法CRK-G、CRK-C、CRK-F 查询所需要的时间。对于数据集Bio-GRID,给定wQ=40,变量k的取值范围为{10,15,20,25,30};对于数据集Email-Enron,给定wQ=11 000,变量k的取值范围为{10,20,30,40,50};对于数据集DBLP,给定wQ=250,变量k的取值范围为{20,30,40,50,60}。
3 种算法随k变化的运行效率对比结果如图5 所示,随着核值k增大,各算法在不同数据集上的查询耗时总体均减少。之所以如此,是因为当给定核值k增大时,得到的候选k核子图规模减小,算法迭代次数减少,故耗时减少。另外,在3 种算法的效率对比中,当k值较小时,CRK-G 算法的查询耗时明显高于另两种算法。
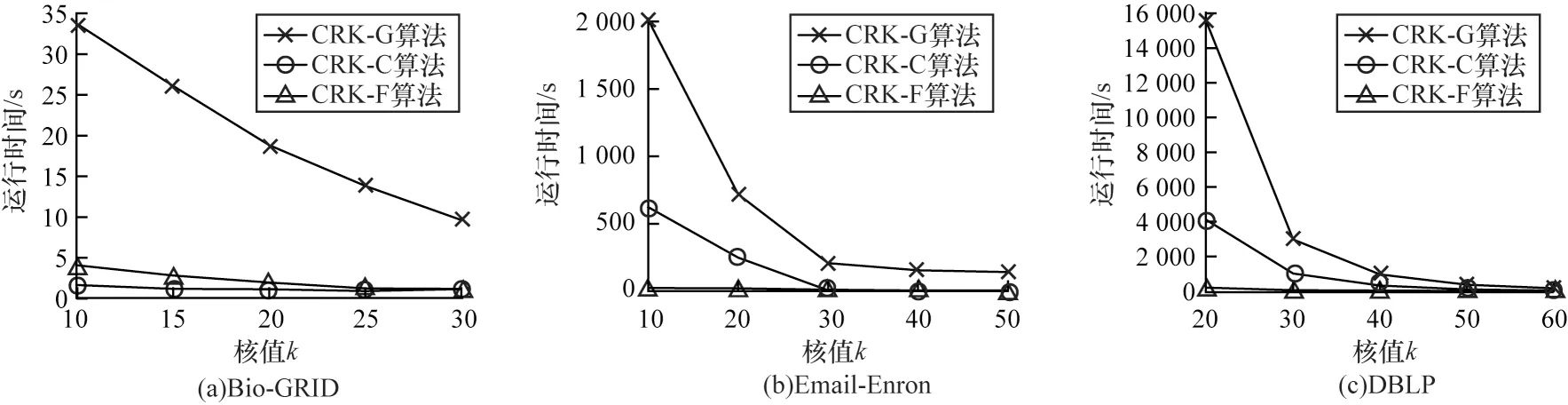
图5 3 种算法随k 变化的运行效率对比Fig.5 Comparison of the operating efficiency of the three algorithms with the change of k
上述实验结果与本文对各个算法的时间复杂度分析结果相符合,CRK-G 算法的查询耗时总体均高于CRK-C 和CRK-F 算法。而CRK-C 算法和CRK-F算法两者耗时大致相近,具体耗时高低主要取决于数据集的特点,当数据集中存在较多权值相近的节点时,图压缩算法压缩后得到的图规模较小,使得CRK-C 算法的查询耗时低于CRK-F 算法。
5.2.2 算法误差分析
由于CRKSQ 问题是NP-难的,无法在多项式时间复杂度内找到最优解,CRK-G 算法虽然能够找到一个可行解,但其与最优解之间的偏离程度无法被预计。CRK-C 和CRK-F 算法是在CRK-G 算法基础上的改进,效率有了很大的提升,但两者相对于CRK-G 算法存在一定的误差。接下来以CRK-G 算法为参考,在不同k值条件下,对CRK-C 和CRK-F 算法查询结果的误差进行分析。
根据算法的原理,评判误差的依据是CRK-C 和CRK-F算法相对于CRK-G算法是否过多删除了节点。实验在3 个数据集上进行:对于数据集Bio-GRID,给定wQ=40,变量k的取值范围为{10,15,20,25,30};对于数据集Email-Enron,给定wQ=11 000,变量k的取值范围为{10,20,30,40,50};对于数据集DBLP,给定wQ=250,变量k的取值范围为{20,30,40,50,60}。
实验记录了各个算法在上述条件下查询得到的子图节点数,计算了CRK-C 和CRK-F 算法相对于CRK-G 算法的误差百分比,结果分别如表2~表4 所示,多次实验的平均误差均在8%以内,误差较小。

表2 Bio-GRID 数据集的查询结果与误差Table 2 Query results and errors of Bio-GRID dataset

表3 Email-Enron 数据集的查询结果与误差Table 3 Query results and errors of Email-Enron dataset

表4 DBLP 数据集的查询结果与误差Table 4 Query results and errors of DBLP dataset
5.2.3 图压缩算法有效性分析
为验证图压缩算法GC-W 的有效性,实验记录了不同k值条件下,GC-W 算法在3 个数据集上压缩候选子图的耗时。
对于数据集Bio-GRID,变量k的取值范围为{10,15,20,25,30};对于数据集Email-Enron,变量k的取值范围为{10,20,30,40,50};对于数据集DBLP,变量k的取值范围为{20,30,40,50,60}。实验结果如图6所示,当k值增大时,压缩时间减少。由于当k值增大时候选k核子图的规模减小,因此压缩算法GC-W 的耗时减少。
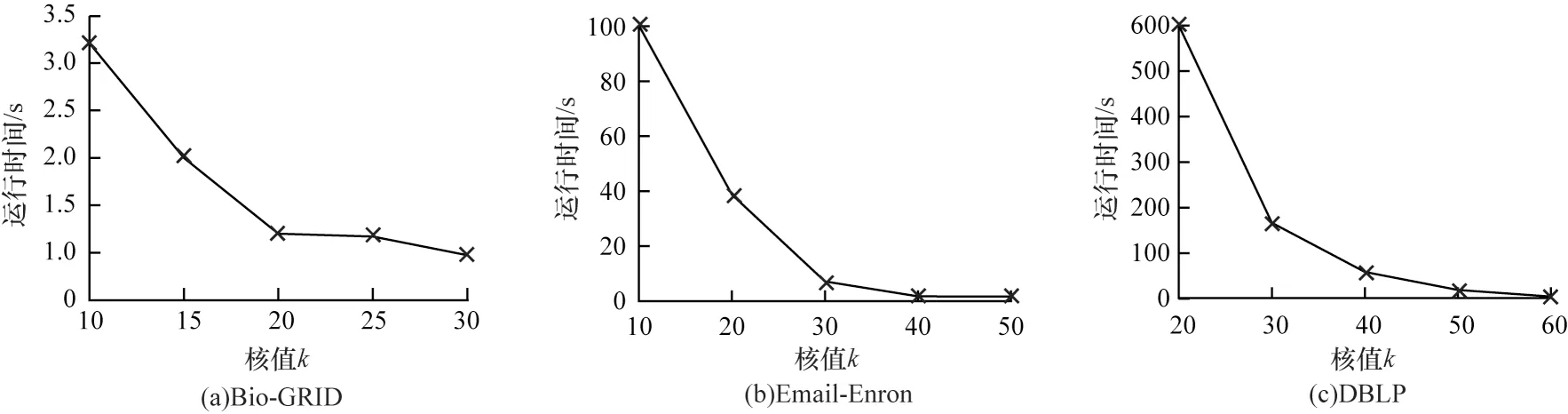
图6 GC-W 算法随k 变化的压缩耗时Fig.6 Compression time of GC-W algorithm with the change of k
压缩耗时相较于查询耗时低了1 或2 个数量级,其可以在相对短的时间内对候选子图进行压缩,有效地减少了查询时间,压缩算法是有效的。
5.2.4 模型有效性分析
为验证紧密k核子图(CRKS)模型的有效性,本文实验对比了CRK-F 算法与忽略权值的k核(k-core)算法,记录两者在不同k值条件下查询得到的子图节点平均权值。
实验分别在3 个数据集上进行,考虑到CRK-F算法和k-core 算法每次查询得到的子图都有可能存在多个,并且前者会由于给定的wQ不同而得到不同的结果。因此,本文将CRK-F 算法在不同wQ条件下查询得到的子图最大节点平均权值与k-core 算法查询得到的所有子图最大节点平均权值进行对比。
对于数据集Bio-GRID,变量k的取值范围为{10,15,20,25,30};对于数据集Email-Enron,变量k的取值范围为{10,20,30,40,50};对于数据集DBLP,变量k的取值范围为{20,30,40,50,60}。实验结果 如图7 所示。从实验结果可以看出,CRK-F 算法得到的子图节点平均权值均大于k-core 算法,验证了CRKS 模型的有效性和优越性。

图7 CRK-F与k-core 算法的子图节点平均权值对比Fig.7 Comparison of average weights of subgraph nodes obtained between CRK-F and k-core algorithms
5.2.5 实例分析
为进一步说明CRKS 模型的合理性,本文选取一个实例进行分析。图8(a)所示是作者协作网络中选取的部分数据,其包含了30 个节点和46 条边,图的节点平均权值为40.67,存在一些联系较为松散的节点。若忽略权值,仅给定k=3,进行3 核查询,查询结果如图8(b)所示。从图中可以看出,虽然所有节点的度均大于等于3,对应着至少3 个邻接节点,但结合边的权值就可发现节点“Bin Zhou”所对应的权值较小,该节点将左右两部分的图连接成一体,使得图整体结构并不紧凑,左右两部分节点之间联系的紧密程度不足。若考虑权值,给定wQ=50,对图8(a)所示的图进行紧密3 核子图查询,得到图8(c)所示的结果。该结果包含两个子图,每个图相较于图8(b),内聚性更强,节点之间的联系也更加紧凑。两个子图的节点平均权值分别为50.8 和53.2,相较于图8(b)的47.08,两个子图整体的联系也更加紧密。

图8 紧密k 核子图的查询实例分析结果Fig.8 Query example analysis results of closely related k-core subgraph
综合上述分析,CRKS 模型可以检测出加权图中紧密联系的子图,相较于现有的方法更加合理有效。
6 结束语
本文提出一种在加权图中查询联系紧密的连通k核子图问题,并证明了该问题是NP-难的。为解决CRKSQ 问题,设计基于贪婪策略的启发式算法CRK-G,其能在可接受的时间内为CRKSQ 问题找到一个近似解,分别从降低图规模和减少迭代次数两个方面出发,提出两个改进算法CRK-C 和CRK-F,其在查询速度上有明显提升。在不同规模数据集上进行多次实验,结果表明,CRK-C 和CRK-F 算法的平均误差都在8%以内。下一步将研究本文算法参数的取值和优化问题,并探索其他更加高效的紧密k核子图查询算法,以满足超大图的查询要求。
