In2Se3 薄膜的掺杂效应及其纳米带铁电性*
2022-10-16黄鸿飞姚杨姚承君郝翔吴银忠
黄鸿飞 姚杨 姚承君 郝翔 吴银忠
(江苏省微纳热流技术与能源应用重点实验室,苏州科技大学物理科学与技术学院,苏州 215009)
低维材料的铁电性一直是凝聚态物理和材料科学领域的研究热点,在新型纳米电子器件的设计和应用等方面有重要的潜在应用和学术价值.本文基于密度泛函理论的第一性计算,以实验上已经验证的二维铁电材料In2Se3 薄膜为出发点,研究了二维In2Se3 薄膜的掺杂效应和In2Se3 纳米带的铁电性.结果发现铁电性和金属性在静电掺杂的In2Se3 薄膜中可以稳定共存,且电子掺杂会同时增强面内和面外极化,空穴掺杂可以增强面外极化,但抑制面内极化,从原子结构畸变和电子结构等角度详细解释了载流子掺杂对薄膜面内极化和面外极化的影响以及物理机制.针对In2Se3 纳米带的研究,发现一维铁电性可以在In2Se3 纳米线中存在,计算并给出了纳米带的局域极化分布和带隙,拟合了带隙和纳米带宽度之间满足 标度关系.以期此研究可为拓宽二维铁电薄膜及其纳米结构的应用提供理论指导.
1 引言
随着器件小型化的迫切需求,找寻超薄铁电薄膜以及探索其铁电性起源在器件应用和学术研究方面都非常有意义.众所周知,传统铁电材料如钛酸铅、钛酸钡等,随着薄膜的厚度变薄,垂直于膜面方向退极化场增强,从而导致铁电性消失,即存在临界尺寸[1],而范德瓦耳斯型低维铁电薄膜,由于无表面悬挂键,在单原子层厚的薄膜中仍然可以保持良好的铁电极化.因此,近年来对范德瓦耳斯型低维铁电材料的实验和理论研究比较活跃,相关的综述文章较多[2-10],其中室温下具有面外自发极化的低维铁电主要有CuInP2S6薄膜[11]、d1TMoS2薄膜[12]、WTe2薄膜[13]等,具有面内极化的铁电薄膜有SnTe 薄膜[14]、GeS 薄膜、GeSe 薄膜[15]等,而α-In2Se3薄膜在室温下具有面内极化同时又具有面外极化,而且两者相互耦合[16,17].In2Se3薄膜还可以和其他材料构建很多新奇功能的异质结[18-22],以及构建铁电隧道结[23]、铁电存储器[24]等.
本文重点研究二维α-In2Se3薄膜的掺杂效应及其纳米带的铁电性,In2Se3薄膜有很多结构,其中α 相是最稳定的结构,α-In2Se3单层薄膜由5 层原子按Se-In-Se-In-Se 顺序构成 (如图1 所示).2017 年Ding 等[25]从理论上预测了α-In2Se3薄膜存在二维铁电性,同年Zhou 等[26]在实验上证实了α-In2Se3薄膜的铁电性.2018 年,Cui 等[16]在In2Se3多层膜中同时观测到了面内和面外极化,并且发现面内极化和面外极化之间的耦合,同年Xue 等[17]在单层膜中利用PFM 方法也观测到了相同的现象,文献[27]报道可以利用MBE 方法可控制备In2Se3薄膜,以上这些理论和实验的研究为In2Se3薄膜的应用奠定了扎实的基础.基于In2Se3薄膜的室温铁电性,Zhai 等[19]研究了HfN2/CrI3/In2Se3的非易失谷极化调控,Zhou 等[20]报道了InTe/In2Se3异质结中的能带调控,Yang 等[21]研究了WSe2/In2Se3作为信息存储物理载体的可行性,Sun 等[22]构建了LaCl/In2Se3异质结研究了磁斯格明子以及磁电耦合效应,所有这些研究表明对单层In2Se3薄膜及其纳米结构进行深入研究是非常必要和有意义的.
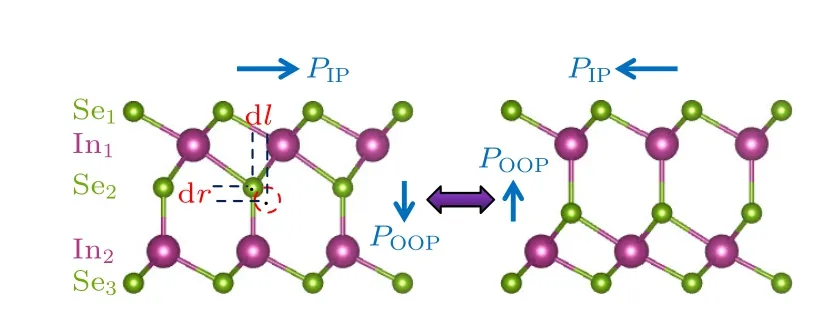
图1 α-In2Se3 单层薄膜结构示意图,其中PIP 表示面内极化,POOP 表示面外极化,dr 和dl 表示铁电相的中间层Se2 原子在面外和面内方向偏移顺电相的位移Fig.1.Structure of ferroelectric α-In2Se3 monolayer,where PIP stands for the in-plane polarization,and POOP denotes the out-of-plane polarization,dr and dl are the distortions of Se2 atom along the out-of-plane and in-plane directions,respectively.
铁电金属的概念最早由Anderson 和Blount[28]提出,直到最近,Shi 等[29]报道了金属LiOsO3从中心对称 (Rc)到非中心对称(R3c)结构的转变,从而首次从实验上证实了极性态和导电态可以共存.利用掺杂可以在铁电材料中实现铁电性和金属性共存,从而拓宽铁电材料在光学[30]和热电[31,32]等领域的应用,还可以设计Mott 多铁材料[33].本文重点关注通过静电掺杂在绝缘的铁电材料中实现铁电极性和金属性共存,这种静电掺杂方法实验上可通过对低维材料施加门电压来实现[34,35].Tsymmbal 等[36]从理论上给出了BaTiO3体材料的临界电子掺杂浓度(0.11 e/u.c.),即当掺杂浓度大于临界值时,铁电性消失.然而,对于孤电子对驱动的铁电体PbTiO3,电子掺杂反而会使极性畸变更显著[37],原因是导致极性畸变的电子分布在低能区(远离费米面).基于第一性原理的计算,Xia 等[38]发现LiNbO3块材中的铁电相甚至在电子掺杂浓度为0.3 e/u.c.时仍稳定存在.随着电子器件小型化的需求,在原子层厚薄膜体系中实现金属铁电相将具有重要意义.文献[39,40]报道了掺杂对具有面外方向铁电极化的PbTe,SiGe,SiSe,GeSn 单层薄膜中的极性畸变影响,静电掺杂对同时有面内和面外极化的铁电薄膜的极性影响尚未见报道.因此,本文对二维In2Se3单层薄膜的掺杂效应进行第一性计算研究,研究发现静电掺杂并不会屏蔽薄膜的铁电畸变,且电子掺杂和空穴掺杂对面内和面外极化的影响不同.
自从二维铁电材料在实验上被发现[14],就开始对更低维度纳米结构的铁电性进行研究.日本京都大学Shimada 等[41]研究了SnTe 纳米带和纳米片的铁电性及其中的极化涡旋,基于第一性计算他们发现SnTe 纳米带的铁电性无临界尺寸,且在SnTe 纳米片结构中发现了极化涡旋.东南大学董帅课题组[42]从理论上预测了GeS 纳米线中的一维铁电性,Fan 等[43]计算并给出了GeSe 纳米带中丰富的电子结构,同时讨论了GeSe 纳米带在器件中的应用.由于技术上已经掌握了如何从二维薄膜通过裁剪方法获得纳米带[44,45],且In2Se3薄膜的极化图像更丰富,因此对In2Se3纳米带进行理论研究很有必要.
本文基于第一性原理计算,从理论上证明了铁电性和金属性可以在掺杂α-In2Se3薄膜中共存,并对相关微观机制进行了详细讨论,拓宽了α-In2Se3薄膜的潜在应用.同时研究还发现α-In2Se3纳米带可以保持良好的铁电性,计算结果表明α-In2Se3纳米带的临界尺寸消失,即当宽度为一个原胞(纳米线)时铁电性仍然存在.期望本研究可以为低维α-In2Se3铁电薄膜及其纳米结构的应用提供理论指导,为基于二维铁电材料的纳米器件设计提供理论支撑.
2 计算方法和结构
本文的密度泛函理论计算中[46],选取Vienna Ab-initio Simulation Package(VASP)软件包中基于广义梯度近似下的Perdew-Burke-Ernzerhof 交换函数(PBE)[47],平面波截止能量设置为500 eV,In 原子的价电子取4d105s25p1,Se 原子的价电子取4s24p4.结构优化过程中,能量收敛标准为10—6eV,力学收敛标准为0.01 eV/Å.此外,真空层厚度设置为18 Å,从而可以忽略周期性超胞间相邻层的相互作用.对于二维薄膜,K点取样为以Г点为中心的8×8×1 网格,而对于纳米带,K点取样则为以Г点为中心的8×1×1 网格.
α-In2Se3薄膜的结构示意如图1 所示,单层薄膜由5 个原子层组成,其中间原子层的Se2 原子相对于顺电相的位移(畸变)对极化的贡献最大,因此在图1 中用dr表示Se2 原子垂直方向的畸变,dl表示平面内的畸变,PIP和POOP分别是平面内的极化和面外极化.薄膜的静电掺杂采用改变体系总电子数的均匀掺杂方案来实现电子掺杂和空穴掺杂[36-38].
In2Se3纳米带的裁剪方式如补充材料图S1 所示,通过沿着平行于薄膜平面内极化方向去裁剪获得纳米带,这样可以更大程度上保持In2Se3纳米带的面内极化.裁剪后得到的纳米带的立体图、俯视图和侧视图如图2 所示,其中b方向真空层的厚度和c方向真空层的厚度取相同值,用w来表示纳米带的宽度,并把w=1 u.c.宽度的纳米带定义为纳米线(一维).
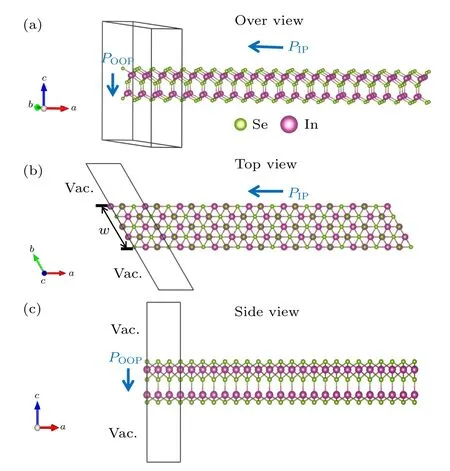
图2 In2Se3 纳米带示意图 (a) 整体图;(b) 俯视图,w 表示纳米带的宽度;(c) 侧视图Fig.2.Illustration of In2Se3 nanoribbon,(a) Over view;(b) top view,w denotes the width of the nanoribbon;(c) side view.
3 结果与讨论
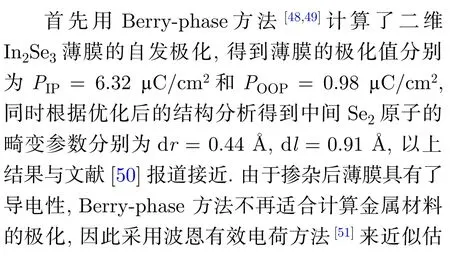

式中vc为原胞体积.对于纳米带由于单胞中各个原胞的极化不一样,因此纳米带的极化是对所有原胞的平均.需要注意的是纳米带中各原子的波恩有效电荷和薄膜的波恩有效电荷是不一样的,特别是纳米带边界处原子的波恩有效电荷跟纳米带中心位置的波恩有效电荷差异较大.在补充材料表S1、表S2 和表S3 中给出了计算得到的宽度为w=1 u.c.,2 u.c.和3 u.c.的纳米带中所有原子的波恩有效电荷,把这些波恩有效电荷和各个原子相对于顺电相的位移代入(1)式就可以估算出纳米带极化.
3.1 薄膜掺杂效应
通过对掺杂薄膜的结构优化,得到了In2Se3薄膜的极化随掺杂浓度的变化规律 (见图3).由图3 可以发现:1)平面内极化随电子掺杂浓度的增大而增大,随空穴浓度的增大而降低;2)无论是电子掺杂还是空穴掺杂,随着掺杂浓度的增大薄膜的面外极化都增强;3)无论是电子掺杂还是空穴掺杂,在掺杂浓度达到0.5 e 时,面内极化和面外极化与未掺杂薄膜相比较变化不大,In2Se3薄膜的掺杂效应跟BaTiO3块材的掺杂效应不同,BaTiO3块材中当电子掺杂浓度大于时铁电极化消失[36].因此,可以得出如下结论,铁电性在掺杂In2Se3薄膜中可以得到很好的保持.同时,在补充材料中给出了Se2原子的结构畸变参数dl和dr随掺杂浓度的变化曲线(见图S2),发现畸变参数的变化规律和极化的变化规律一致.与其他二维铁电薄膜的掺杂效应相比,如在只有垂直极化的皱褶结构的SiSe 薄膜中[40],电子掺杂会增强极化,而空穴掺杂则降低极化,与In2Se3薄膜面外极化的掺杂效应不同;在只有面内极化的SnSe 薄膜中空穴掺杂存在临界浓度与In2Se3薄膜面内极化的掺杂效应也不同,这是由于In2Se3薄膜既有面内极化同时又存在面外极化的特殊性以及与In2Se3薄膜的电子结构相关的.
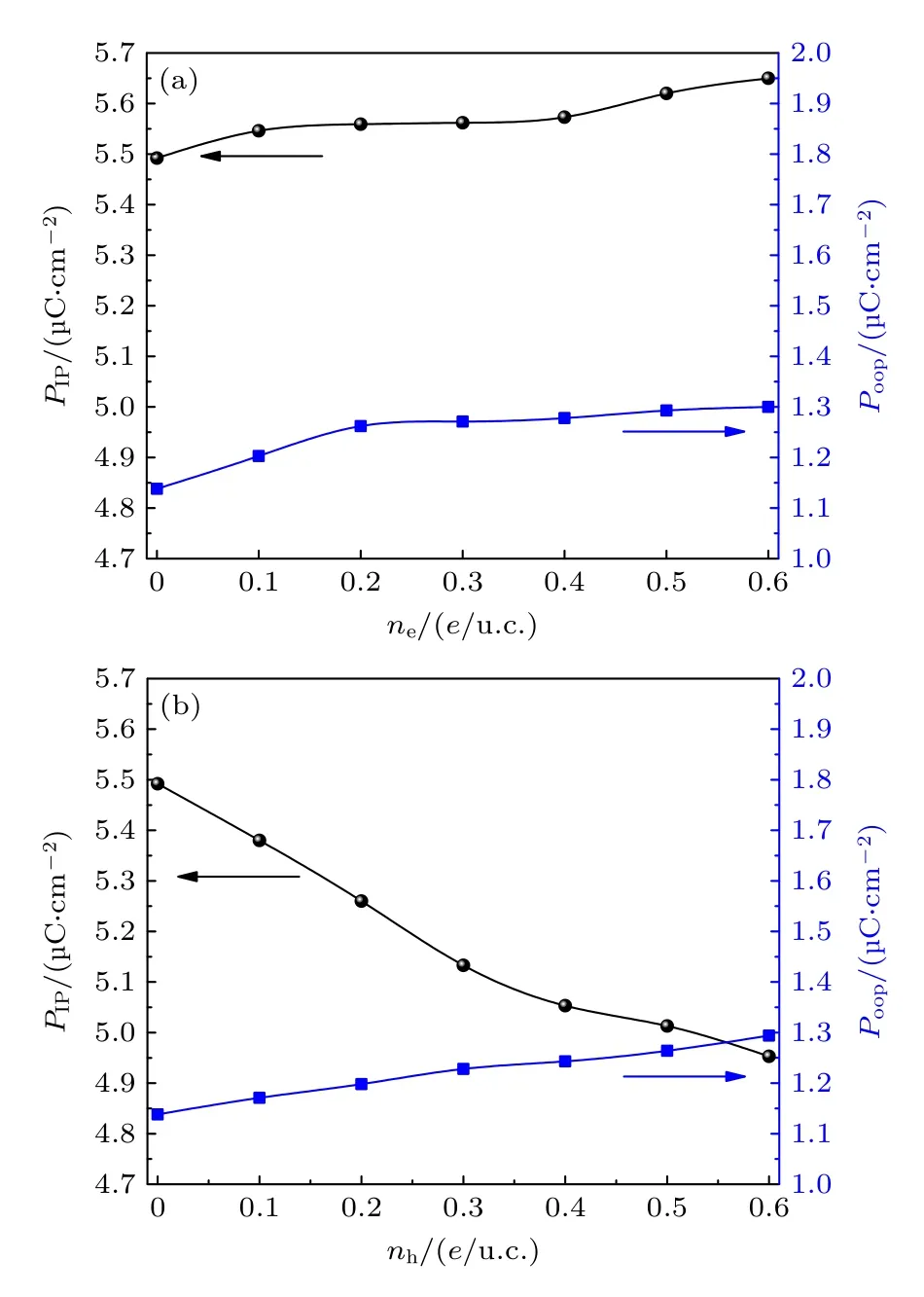
图3 In2Se3 薄膜的极化随掺杂浓度的变化 (a)电子掺杂;(b)空穴掺杂Fig.3.The in-plane and out-of-plane polarization of In2Se3 monolayer as a function of doping concentration for the case of (a) electron doping and (b) hole doping.
未掺杂In2Se3薄膜的轨道投影电子态密度和电子(空穴)掺杂浓度为ne=0.3 e/u.c.(nh=0.3 e/u.c.)的轨道投影电子态密度图如图4 所示,对电子态密度的分析可以得出: In2Se3薄膜的价带顶由Se 原子的px和py轨道组成,导带底主要贡献为In的s 轨道和Se的p 轨道(px,py,pz).因此电子掺杂时,掺入电子将占据导带底附近In的s轨道和Se的p 轨道(px,py,pz),从而增强了In 原子和Se 原子之间的sp 杂化,因此电子掺杂必然会同时增强薄膜的PIP和POOP.而当空穴掺杂时,掺入空穴则主要占据价带顶处Se 原子的px和py轨道,对Se 原子的pz轨道占据情况影响较小,同时考虑到空穴掺杂会导致晶体体积收缩,因此空穴掺杂会导致薄膜的PIP降低和POOP增大.以上从薄膜的电子结构特征解释了图3 中In2Se3薄膜在电子掺杂和空穴掺杂情况下的极化变化规律,同时在补充材料中给出了掺杂In2Se3薄膜的局域电子密度图(见图S3).In 原子的5S2 孤电子对对In2Se3薄膜铁电稳定性有贡献[53],通过观察面外极化朝下的In2Se3薄膜(图S3(a)),In1原子在深能区的5S2孤电子对比In2原子的5s 电子的局域化程度更明显,而且比较图S3(b),(c)和图S3(a),发现无论掺杂电子还是空穴对孤电子对的空间分布影响很小,这一现象是由于孤电子对处于远离费米面的低能区所致,也正是由于孤电子对在高掺杂浓度下的相对稳定性,导致了In2Se3薄膜在掺杂情况下库仑屏蔽效应不明显,仍可以保持相当强的面内极性和面外极性,这类似于PbTiO3块材在掺杂情况下孤电子对极性畸变的贡献[37].由图1 可知,单层In2Se3薄膜有5 个原子层,极化主要是由中间Se2原子层的极性畸变所贡献,在电子掺杂和空穴掺杂情况下,通过电子态密度的分原子层和分轨道投影图(见补充材料图S4)可以看出: 对于空穴掺杂,载流子主要占据Se1 和Se2的Pxy轨道(见图S4(a)),因此会导致平面极化的部分屏蔽,即随着空穴掺杂浓度的提高,平面内极化降低;电子掺杂时,载流子不会占据中间Se2原子层(见图S4(b)),传导电子主要集中在薄膜的下表面,而不会影响与电极化相关的中间Se2 原子层的相关电子转移,因此铁电性(特别是垂直于薄面方向的铁电性)更易在实验中被观测到.
3.2 纳米带的尺寸效应
In2Se3纳米带的极化计算结果表明(见图5):随着纳米带宽度的变小,面内极化和面外极化均降低,但是有两个有意义的例外,一是当纳米带的宽度为2 u.c.时,面内极化反而增强且略大于薄膜的面内极化值,二是一维In2Se3纳米线(w=1 u.c.)的垂直于纳米线方向极化值为比二维薄膜的面外极化提高了30%,因此In2Se3纳米结构具有稳定的铁电性,且In2Se3纳米带的铁电性不存在临界尺寸,与SnTe,GeS 纳米带的结论一致,但不同的是SnTe,GeS 纳米带的极化方向平行于纳米线[41,42].下面分别从晶格常数的变化以及微观极化分布来解释In2Se3纳米线和纳米带(w=2 u.c.)拥有上述有趣现象的物理起源.
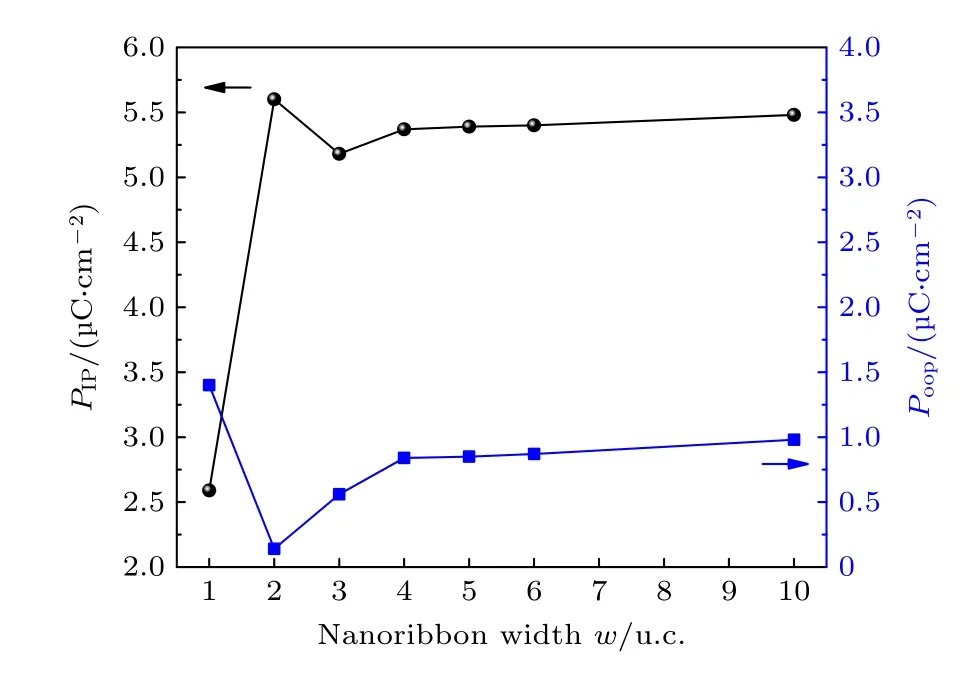
图5 纳米带极化随纳米带宽度变化曲线Fig.5.Polarization of In2Se3 nanoribbons as a function of the width.
首先由图6 可以看出,随着纳米带的宽度降低,面内的晶格常数a 和纳米带的厚度t变化很小,直到宽度降到2 个原胞厚度及1 个原胞厚度时,晶格常数才会发生明显变化.对于2 个原胞厚度的纳米带,由于面内晶格常数变化不大而面外晶格常数减小了0.4 Å,也就是说由于垂直方向的晶格收缩导致了面内极化的增强,后文将进一步说明晶格垂直方向的收缩效应还和垂直方向反铁电畴的形成有关.图6 中纳米线的面内晶格常数为6.7 Å,比两个原胞厚度的纳米带的面内晶格常数收缩了0.3 Å,同时纳米线厚度t也明显变薄,由此引起垂直于纳米线方向的极化POOP增强.
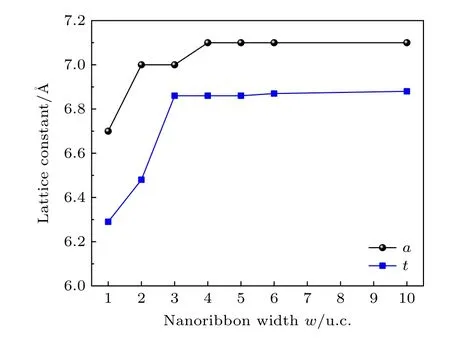
图6 In2Se3 面内晶格常数a 和厚度t 随纳米带宽度w 变化曲线Fig.6.The in-plane lattice constant a and the thickness t of In2Se3 nanoribbon as a function of the width w.
采用波恩有效电荷方法计算出了In2Se3纳米线和纳米带的局域极化,图7 给出的是w=1 u.c.,2 u.c.,3 u.c.和4 u.c.的纳米带的极化分布,更宽纳米带的极化分布图见补充材料(图S5,w=5 u.c.,6 u.c.和10 u.c.).图7 中各原胞内的矢量表示该原胞平面内极化的大小和方向,同时原胞内填充不同的颜色表示面外极化的大小和方向,正的数值代表面外极化朝上,负值表示面外极化方向朝下.先观察图7 中的平面内的极化: 在纳米带的中心位置平面内的极化几乎平行于纳米带带边方向,而边界单元的面内极化指向略偏向带边,且纳米带内部的极化大于边界处的极化,整体上面内平均极化平行于带边,在纳米带宽度方向宏观极化为零,因此宽度方向纳米带的退极化能也为零.纳米带的面外极化局域分布特点可以归纳为以下几点: 1)带边的面外极化和纳米带内部的面内极化方向相反,这样有利于降低体系的退极化能;2)纳米带中心的面外极化最弱,即面外极化绝对值最小;3)对于宽度为2 个原胞的纳米带,垂直于膜面方向形成了反铁电畴,面外平均极化趋于零,这也是2 个原胞宽度的纳米带的面内极化大于二维薄膜面内极化的原因;4)对于一维纳米线,由于平行于纳米线方向的极化相比于纳米带的面内极化降低了一半(见图5),导致了垂直于纳米线方向的极化大于二维薄膜的面外极化值.
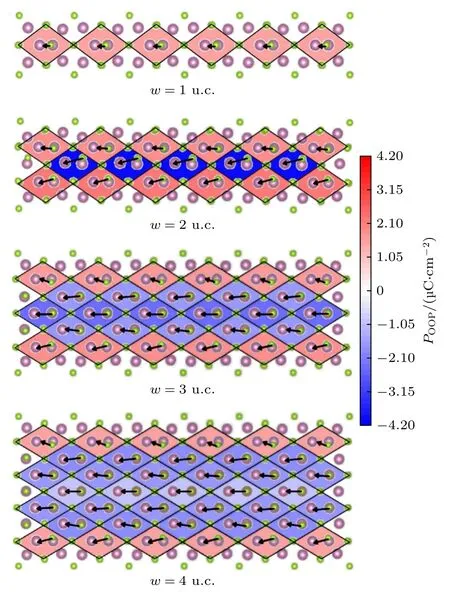
图7 纳米带极化分布图(纳米带宽度分别为1 u.c.,2 u.c.,3 u.c.和 4 u.c.),其中平面内极化大小和方向用矢量表示.垂直平面的极化大小用颜色来表示,且负号代表面外极化方向朝下,正号代表面外极化朝上Fig.7.Distribution of polarization within In2Se3 nanoribbon with different width (w=1 u.c.,2 u.c.,3 u.c.and 4 u.c.),where the magnitude and the direction of PIP are indicated by vector,the magnitude of POOP is described by different color,and the positive value of POOP denotes the up direction and negative value denotes the down direction.
最后计算并画出了纳米带带隙随纳米带宽度的变化曲线(见图8),由于宽度方向的空间局域效应,随着纳米带宽度的变窄,带隙增大,这符合量子局域规律.同时采用文献[54,55]给出的纳米带带隙和宽度拟合公式其中为薄膜的带隙,c为常数,w为纳米带的宽度,β为标度指数.通过对In2Se3纳米带带隙拟合,得到c=0.36,β=2,这表明In2Se3纳米带带隙的标度律为1/w2,与沿Armchair 方向裁剪的黑磷纳米带带隙的标度律一致[54].
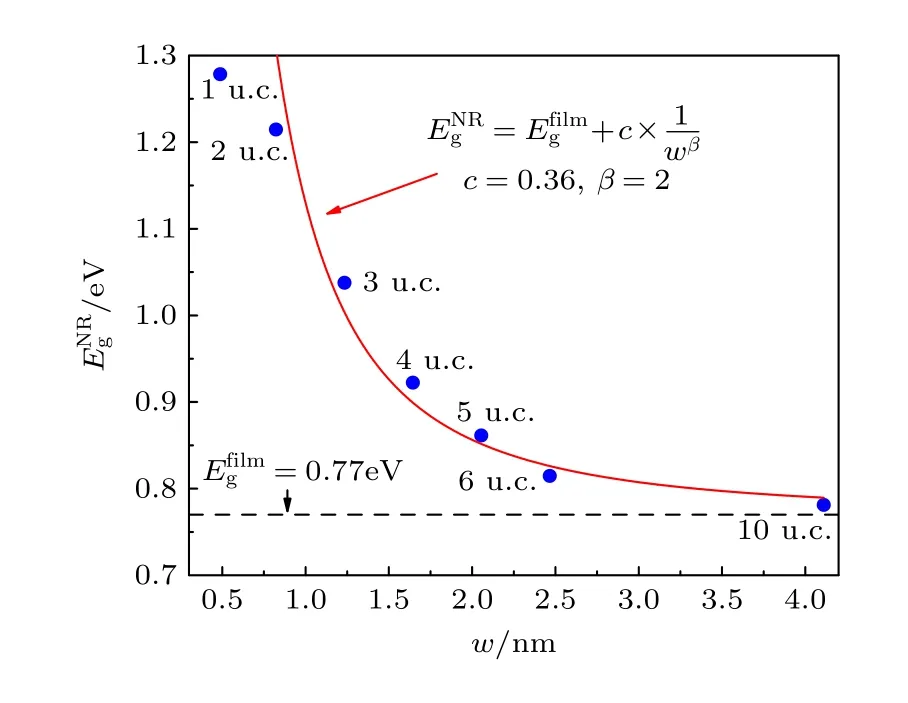
图8 In2Se3 纳米带带隙随纳米带宽度的变化曲线,图中水平短划线(黑色)是薄膜的带隙,实线(红色)是拟合曲线Fig.8.Band gap of In2Se3 nanoribbon as a function of the width of nanoribbon,where the dashed line denotes the band gap of monolayer,and the red solid line is the fitted curve.
4 结论
基于密度泛函理论,从理论上研究了掺杂对In2Se3薄膜铁电性的影响,证实了铁电性和金属性可以共存,且电子掺杂和空穴掺杂对薄膜面内和面外铁电极化的影响不同: 电子掺杂会增强面内面外极化,而空穴掺杂会导致面内极化减弱,面外极化增强,二维In2Se3薄膜的静电掺杂效应与传统的铁电材料以及最新报道的二维铁电材料的掺杂效应均有所不同,有意义的是高浓度掺杂对极化大小的影响不大,因此掺杂In2Se3薄膜是一个理想的二维金属铁电薄膜.由于二维室温铁电性在In2Se3薄膜中已经得到实验证实,因此针对In2Se3纳米带的理论研究就更具实际意义.第一性计算结果表明: 一维铁电性可以在In2Se3纳米线中出现,我们详细分析了不同宽度纳米带的面内和面外极化分布,并拟合得到了In2Se3纳米带带隙和宽度之间的变化规律期待本文关于In2Se3薄膜的二维金属铁电性的稳定性研究和In2Se3纳米带中低维铁电性的预测可以为新的纳米光电和热电电子器件设计和应用提供新思路.
