基于细观损伤力学的四级配混凝土立方体试件单轴破坏有限元分析

糜凯华 邓水明

(中水珠江规划勘测设计有限公司，广东 广州 510610)

水利工程中混凝土挡水坝由于尺寸大,通常采用四级配混凝土,该级配混凝土粗骨料粒径最大可达150mm,而且骨料含量占比大。由于技术条件的限制,过去主要运用简单易行的湿筛法分析四级配混凝土的力学性能,不过该方法改变了混凝土中粗、细骨料和水泥浆的组成比例,因此用湿筛小试件力学性能近似四级配混凝土的力学性能显然不够合理。进行大规模的混凝土力学性能试验,需要较大的人力、物力,而试验结果受各因素的制约,也只能近似反映其力学指标[1]。

随着混凝土材料在复杂结构上的运用越来越广泛,一直以来对混凝土破坏的力学机制研究从未间断过。为了在细观尺度上合理地分析混凝土的力学性能和破坏机理,很多研究者从不同角度构建了不同的细观模型,如格构模型[2]、MFPA细观模型[3]。本文简要介绍混凝土损伤塑性模型的基本特点,然后基于混凝土损伤塑性模型在静荷载作用下对混凝土立方体试件进行二维有限元分析,分析混凝土骨料、界面、砂浆基体参数对混凝土宏观破坏的影响。

1 细观各相材料本构关系

混凝土损伤塑性模型[4]是一个基于塑性的连续介质损伤模型。该模型考虑了材料拉压性能的不同,在单向加载情况下材料因损伤导致的永久退化具有良好的收敛性。

混凝土损伤塑性模型被广泛运用于混凝土损伤分析中,使用该模型的要点在于如何定义损伤因子与应变的关系。如分析过程中未给出损伤和应变的关系,则该模型只能分析混凝土的塑性变化过程。当缺少混凝土各相材料的应力与应变关系数据时,采用混凝土结构设计规范推荐的单轴本构关系推导各相材料的本构关系,从而实现四级配混凝土细观力学有限元分析。在单向加载的情况下,达到极限应力后采用式(1)、式(2)计算混凝土进入软化阶段后的应力应变关系数据。

单轴荷载情况下的损伤因子与应变的关系根据能量等效的原理推导:

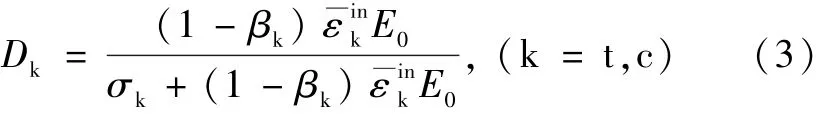
以上式中:t,c分别表示拉伸和压缩;为非弹性应变;βk为塑性应变在非弹性应变中比例为损伤因子。

2 混凝土单轴破坏有限元分析

为分析混凝土不同骨料分布、骨料形状、界面厚度、界面及砂浆基体强度对混凝土宏观破坏的影响,探索混凝土在荷载作用下的裂纹扩展规律[5],根据《水工混凝土试验规程》(SL 352—2020)[6],选取混凝土单轴拉伸、压缩试验二维试件尺寸均为0.45m×0.45m。按文献[7]中混凝土各相材料的比重构建混凝土二维细观有限元模型。模型中粗骨料粒径80～150mm、40～80mm、20～40mm、5～20mm的面积率分别为0.1687、0.1676、0.1206、0.0854,骨料总含量为54.23%。在进行混凝土单轴破坏有限元分析时,粗骨料本构关系采用线弹性模型,界面及砂浆基体的本构关系采用损伤塑性模型。混凝土细观各相材料的计算参数参照文献[8-13]取得,见表1。

表1 混凝土细观各相材料计算参数

按照定义混凝土损伤塑性模型相关数据的方法,由表1中数据计算得到混凝土细观各相材料进入塑性阶段后的损伤因子与应变的关系曲线,见图1和图2。屈服应力与开裂应变及非弹性应变的关系曲线见图3和图4。

图1 损伤因子-开裂应变曲线

图2 损伤因子-非弹性应变曲线

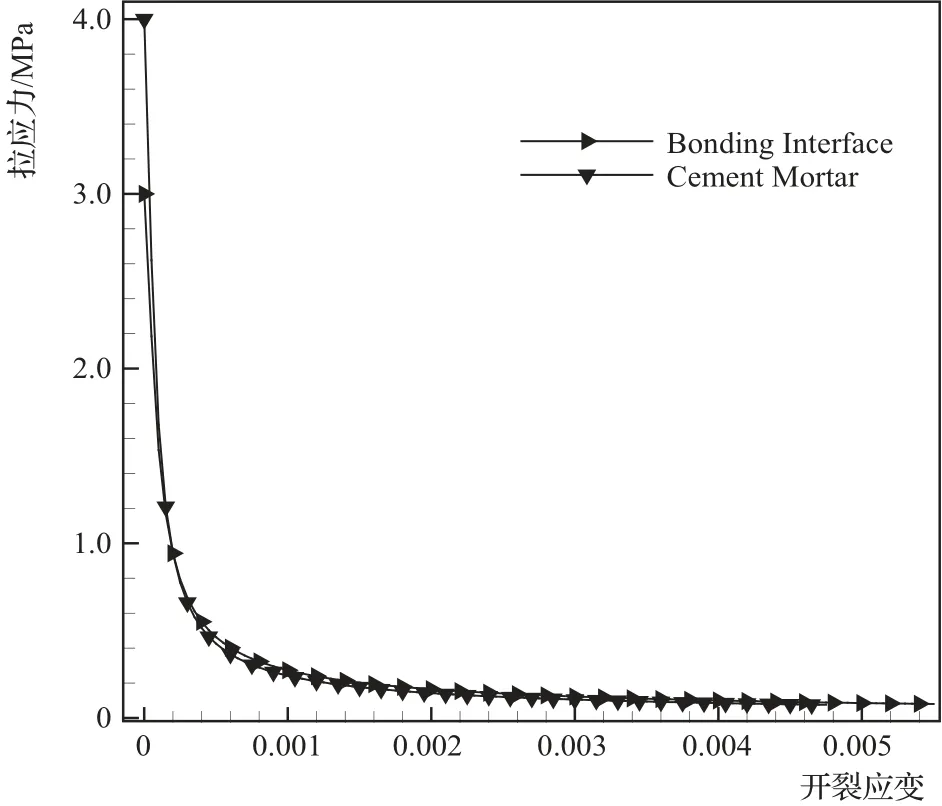
图3 应力与开裂应变曲线

图4 应力与非弹性应变曲线

二维混凝土细观有限元模型的边界条件为试件左端所有节点横向竖向自由度为零,为获得混凝土在单向加载情况下应力-应变曲线的软化段,在试件右端所有节点采用位移加载。

2.1 骨料分布及形状对混凝土宏观破坏的影响

根据前述骨料含量及混凝土损伤塑性模型参数的定义,对圆形、多边形、椭圆形骨料分别构建6组二维混凝土细观有限元模型进行单轴拉伸、压缩情况下的损伤破坏分析。三种骨料形状的二维混凝土细观有限元模型在单轴拉伸、压缩情况下的应力-应变曲线分别见图5和图6;不同骨料参数的二维混凝土细观有限元模型在单轴拉伸荷载作用下的宏观破坏形态分别见图7和图8;不同骨料参数的二维混凝土细观有限元模型在单轴压缩荷载作用下的宏观破坏形态分别见图9和图10。

从图5可知,混凝土的应力未达到极限抗拉强度时,应力-应变呈线性变化;应力超过极限抗拉强度后,承载力不再提高但应变急剧增长,整个破坏过程历程短,表明混凝土的受拉破坏为脆性破坏。多边形、圆形、椭圆形骨料二维混凝土细观有限元模型的极限抗拉强度分别为1.84MPa、1.76MPa、1.78MPa,说明碎石骨料混凝土较卵石骨料混凝土极限抗拉强度略高。

图5 细观模型单轴拉伸情况下应力-应变曲线

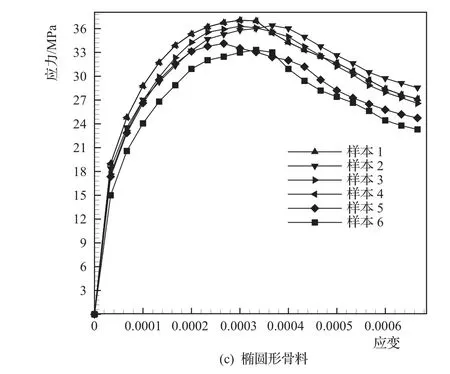
图6 细观模型单轴压缩情况下应力-应变曲线

图7 不同骨料形状样本1单轴拉伸最终破坏形态

图8 不同骨料形状样本2单轴拉伸最终破坏形态

图9 不同骨料形状样本1单轴压缩最终破坏形态

图10 不同骨料形状样本2单轴压缩最终破坏形态

从图6可看出,混凝土的应力小于极限抗压强度0.4倍时,应力-应变曲线呈直线形式变化;随着荷载的不断增加,混凝土表现出一定的塑性特性,此时应力-应变呈曲线形式变化;当混凝土的应力超过极限抗压强度后,承载力不再增加而应变却迅速增长。多边形、圆形、椭圆形骨料二维混凝土细观有限元模型的极限抗压强度分别为35.89MPa、34.42MPa、35.10MPa,说明碎石骨料混凝土较卵石骨料混凝土极限抗压强度略高。

上述混凝土试件的最终破坏形态表明:不同骨料分布的二维混凝土细观有限元模型在单向荷载作用下呈现出不同的裂纹发展形态。由于混凝土材料的特殊性,裂缝主要起于骨料与砂浆基体之间的界面并沿着骨料边界扩展,当荷载继续增加时,裂缝经界面延伸至砂浆基体内部并迅速蔓延,混凝土试件逐渐失稳破坏,丧失承载能力后最终出现断裂。因粗骨料强度和断裂能较其他两组分高,粗骨料内部几乎不会出现断裂,说明粗骨料对裂纹扩展有阻碍作用。混凝土试件单轴拉伸荷载作用下的破坏形态表现为断裂形式,主要是由于混凝土内部形成一条主裂纹造成混凝土试件的断裂;混凝土试件单轴压缩荷载作用下的破坏形态表现为自由面向外膨胀而呈现出破碎状态,主要是由于混凝土内部出现多条平行裂纹,自由边界向外膨胀所致。

2.2 界面厚度对混凝土宏观破坏的影响

界面是位于粗骨料与砂浆基体之间力学性能比较差的介质,混凝土内部的初始损伤往往就出现在界面内。基于前述的骨料比重及损伤塑性模型参数的定义,对多边形骨料生成不同界面厚度的二维混凝土细观有限元模型,以分析不同界面厚度对混凝土宏观破坏性质的影响,不同界面厚度的二维细观有限元模型的数值分析结果见表2。

表2 界面厚度对混凝土宏观破坏的影响

从表2可看出随着界面厚度的减小,混凝土试件的极限强度有所增长。界面厚度每降低1.5mm,混凝土试件的单轴拉、压极限强度增幅分别为5.6%、8.9%。由于界面是混凝土内部薄弱层,界面厚度越小,其对混凝土内部结构的弱化也就越小。

2.3 界面和砂浆基体强度对混凝土宏观破坏的影响

通过前述骨料占比及混凝土损伤塑性模型参数的定义,建立多边形骨料二维混凝土细观有限元模型进行有限元分析,分析过程中调整界面和砂浆基体的抗拉、抗压强度,分析界面和砂浆基体的强度对混凝土宏观破坏时极限强度的影响。界面和砂浆基体抗拉、压强度分别按步长0.5MPa、5.0MPa逐级递减。其计算参数及计算结果见表3。

表3 界面和砂浆基体强度对混凝土试件宏观破坏的影响 单位:MPa

由表3数据可得出,界面抗拉、压强度逐级降低时,试件宏观抗拉、抗压强度降幅分别为55.9%、24.1%,表明混凝土试件宏观抗拉、抗压强度受界面强度影响较大;界面的强度越高,混凝土宏观破坏时的极限强度也越高。砂浆基体抗拉、抗压强度逐级降低时,混凝土试件宏观抗拉、抗压强度降幅分别为38.1%、22.2%,表明砂浆基体的强度对混凝土试件宏观破坏时极限强度的影响较小。

3 结 论

四级配混凝土试件在静载作用下的单轴拉伸、压缩有限元分析结果表明:不同骨料参数下的二维混凝土细观有限元模型极限强度略有不同,但数值分析结果基本上与工程实际吻合。界面厚度减小时混凝土宏观破坏的极限强度反而增加,另外界面和砂浆基体强度降低,混凝土试件宏观破坏的极限强度也随着降低,但界面强度对混凝土宏观破坏时的强度影响更大,表明引起混凝土力学性质弱化的内在原因是界面,破坏过程中初始损伤也最先产生于界面内部。混凝土因其骨料粒径较大,大骨料明显可阻碍裂纹进一步扩展,裂纹扩展时避开骨料并沿着阻力最小路径进行。