面向在轨靠泊加注的管路力学分析与优化设计

孙志成，李世鹏，宋晓东，黄奕勇，张 欢，闫明政

(1. 北京理工大学宇航学院，北京 100081; 2. 飞行器动力学与控制教育部重点实验室，北京 100081；3. 军事科学院国防科技创新研究院，北京 100071)

0 引 言

随着航天探索的不断深化，航天器推进剂在轨补给技术的重要性已逐渐凸显。一方面，越来越多的航天器因推进剂耗尽而成为失效航天器，不但占据了宝贵的轨道资源，而且迫使人类发射相同功能的航天器替代它们，利用在轨补给技术则可以节约轨道资源与地球资源；另一方面，人类已不满足于地球周边的太空活动，并逐步开展对火星等行星的深空探测活动，这也需要该技术的支持。

推进剂在轨补给方式可分为直接加注、更换推进模块和增加推进模块三种，直接加注方式凭借其易操作性而被广泛应用。对于直接加注，服务航天器和客户航天器之间需要先进行连接，再进行加注。连接方式可分为碰撞连接与靠泊连接两种。碰撞连接为漂浮式连接，碰撞力较大且存在失败风险；靠泊连接为抓取式连接，两航天器之间依靠机械臂连接成为一个相对稳定的整体，之后再由机械臂将航天器拉回或者由航天器伸出一个对接机构进行连接，碰撞力较小且成功概率大。由于伸出对接机构的靠泊连接方式(简称伸出式靠泊连接)具有运动质量小的特性，使得其碰撞力远远小于其他连接方式，有助于延长航天器的服役寿命，其连接过程如图1所示。因此，对于需要连接的在轨任务(例如推进剂的在轨直接加注)，伸出式靠泊连接拥有良好的应用前景。

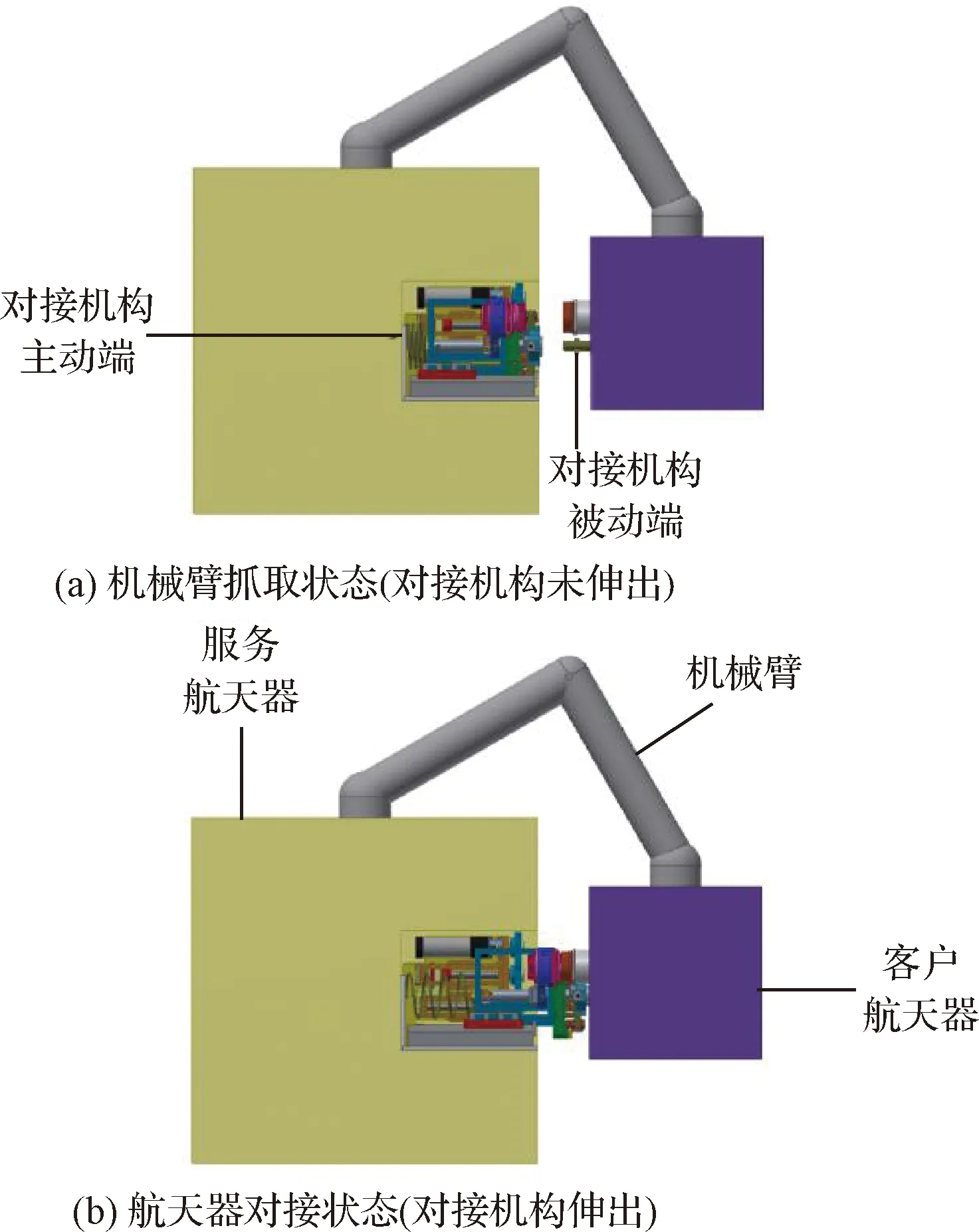
图1 伸出式在轨靠泊连接过程Fig.1 Joining process of on-orbit stretching berthing

对于伸出式靠泊连接在轨直接加注任务，其加注管路会随对接机构同步外伸，如图2所示。考虑到推进剂与加注管路的相容性以及推进剂的高压性，加注管路的材料多采用钛合金或者铝合金等硬质金属。因此，加注管路的拉伸势必会产生附加力，使对接机构造成额外功耗甚至影响对接。因此，对加注管路的力学特性进行分析，并根据分析结果设计加注管路构型从而降低管路附加力具有重要的研究意义。

图2 伸出式在轨靠泊加注任务加注管路状态Fig.2 Refueling pipeline status in the on-orbit stretching berthing task

针对沿单一方向进行拉压的管路，类弹簧的螺旋线构型因其轴向刚度低的优势而成为一种合适的选择。同时，考虑到在轨机构的紧凑性，加注管路的设计空间多是有限且非规则的空间。在这种情况下，偏置拉压椭圆螺旋管路的单圈长度相比于中心拉压的圆螺旋管路更长，从而具有更小的轴向刚度(附加力)。因此，需要研究偏置拉压椭圆螺旋管路的轴向刚度问题。

目前国内外还没有关于椭圆螺旋结构轴向刚度的相关研究，但圆螺旋结构的类似研究已较为深入。刘鸿文采用能量法与微元法推导得到圆螺旋弹簧的经典刚度公式，但没有考虑剪切作用。骆振兴等则考虑了剪切作用、转动惯量以及螺旋升角对弹簧刚度的影响，并计算得出当螺旋升角小于5°时，弹簧旋绕比越小传统刚度计算公式的误差越小的结论。Dym考虑了拉伸与扭转的耦合效应，利用最小总势能原理推导得到弹簧刚度的表达式。张健等以几何精确梁方法对圆截面螺旋弹簧进行建模，推导得到弹簧的变形虚功率方程，并分析了弹簧刚度的非线性特性。以上均是关于圆螺旋结构的研究，对于椭圆螺旋结构的研究还有待深入。

在轨加注管路的设计需要在有限且不规则的设计空间内得到附加力最小的构型(包括位置参数和构型参数)，这是一个典型的多维非线性约束工程优化问题。目前，针对该类问题，代理模型被广泛应用以提高计算效率。主流的代理模型包括：多项式响应面、径向基函数、神经网络以及克里金代理模型(KRG)。其中，KRG的综合性能相比于其他几种代理模型具有显著优势。近年来，基于代理模型的进化算法也在不断发展。该方法通过进化获得后代种群，通过代理模型预测后代种群，在种群进化的同时更新代理模型，极大地提升了计算效率。对于约束优化问题，Wang等提出了一种基于进化采样与罚函数的优化算法，但该方法对罚函数的选取有极高要求，会出现结果不收敛的情况。为避免罚函数选取不当的问题，Wang等提出了一种基于全局与局部代理模型的差分进化算法，但该方法需要反复调用原分析模型，导致计算效率不高。Long等提出了一种基于知识转移采样的代理辅助差分进化算法，该方法将知识转移采样方法与基于克里金代理模型的约束差分进化算法(Kriging assisted constrained differential evolu-tion, KRG-CDE)相结合，细化了初始样本点，提高了优化问题的结果收敛性和计算效率。

本文面向伸出式靠泊加注任务，提出了一种偏置椭圆螺旋加注管路构型。首先，基于能量法-微元法与第三强度理论推导了该类管路的轴向刚度表达式与应力数学表达式。之后，对轴向刚度及应力进行了仿真校验，对轴向刚度进行了实验校验。最后，以非规则设计空间边界、工作应力、对接行程和偏置力矩为约束条件，轴向刚度最小为优化目标，采用KRG-CDE对某在轨加注对接机构非规则设计空间下的偏置椭圆螺旋管路进行了构型优化设计，形成了一套完整的在轨加注椭圆螺旋管路设计方法，并将偏置椭圆螺旋管路同无偏圆、无偏椭圆以及偏置圆螺旋管路的最优构型进行对比，验证了偏置椭圆螺旋加注管路附加力更小的优越性。

1 偏置椭圆螺旋管路力学特性分析

伸出式靠泊加注对接任务主要可分为抓取和对接两个过程。在对接过程中，加注管路随对接机构沿对接方向同步外伸，所形成的管路附加力将造成额外功耗甚至影响对接。同时，在轨机构的紧凑性又决定了加注管路的设计空间是有限且不规则的，故需要在有限的设计空间内设计加注管路，以降低管路拉压所形成的附加力。

1.1 管路力学建模

基于加注管路单方向拉压与设计空间不规则的特性，本文提出了一种偏置椭圆螺旋加注管路构型，如图3(a)所示，图中：为管路承载点；为管路固定点；为管路中心点；为管路在点受到的轴向外力。为了降低管路附加力，管路被设计成初始为压缩态，终止为拉伸态，且拉压变形量相同，此种设计可使管路的拉压极限附加力相等且最小,如图3(b)所示，图中：为管路对接行程；为管路螺距；为管路外径；为管路螺旋升角；为管路自由态长度；为管路有效圈数。

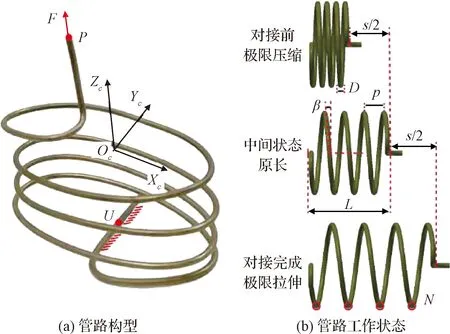
图3 偏置椭圆螺旋加注管路Fig.3 A bias-loading elliptical-helical refueling pipeline

由于在轨机构的紧凑性，加注管路的设计空间和结构都必然紧凑，螺旋升角一般都小于5°，故可忽略螺旋升角的影响，从而将三维问题转变为二维问题。图4为偏置椭圆螺旋管路的俯视平面关系简图，图中为椭圆管路的任意螺旋截面。

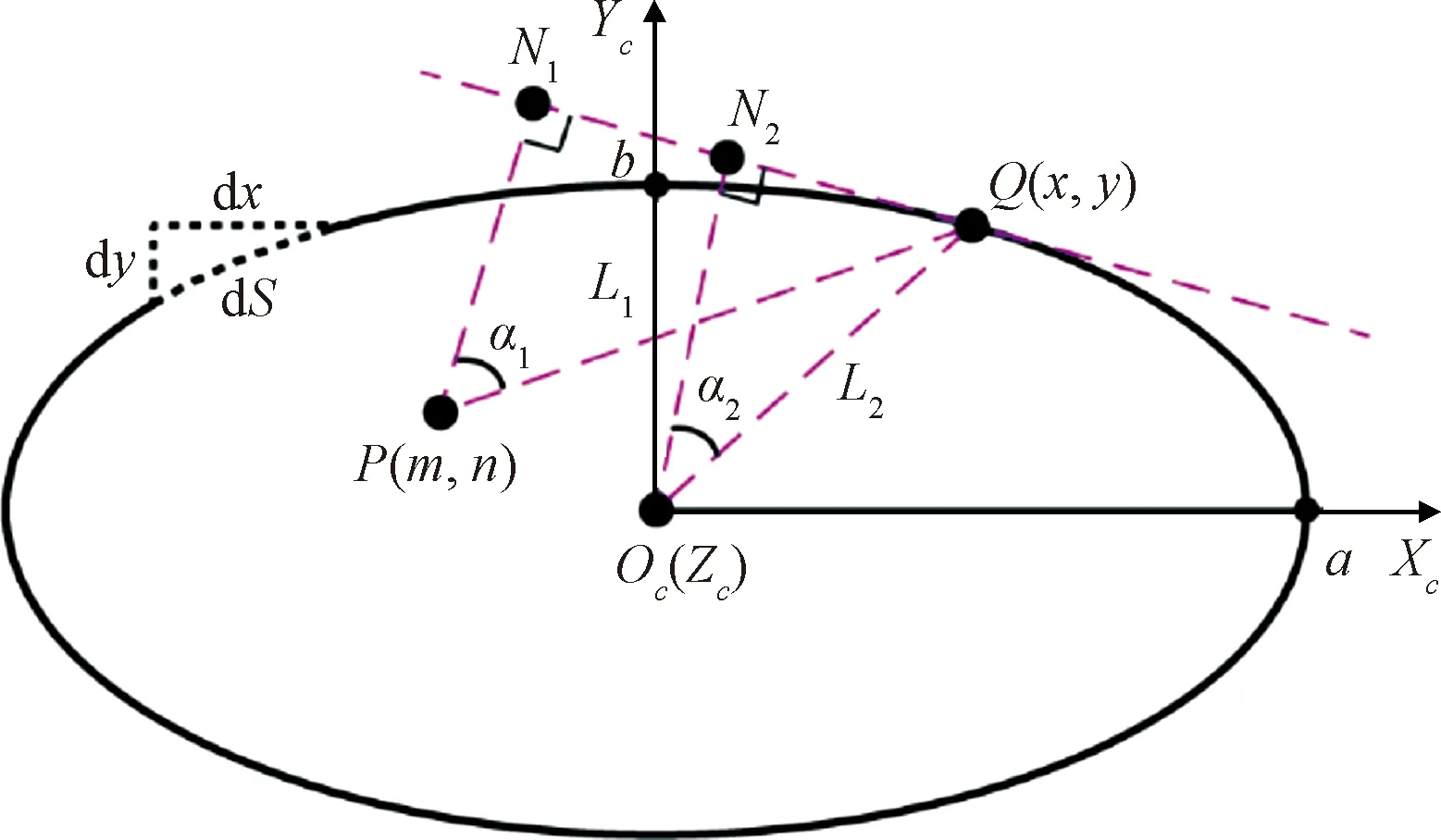
图4 椭圆螺旋管路平面几何关系Fig.4 Geometrical relations of an elliptical-helical pipeline

如图4所示，椭圆管路方程为

(1)

式中：为椭圆管路长半轴；为椭圆管路短半轴；为椭圆管路参数方程参数。

根据式(1)和图4，可得椭圆管路任意螺旋截面切线的垂线和椭圆管路承载点与椭圆管路任意螺旋截面的连线的夹角∠，记为：

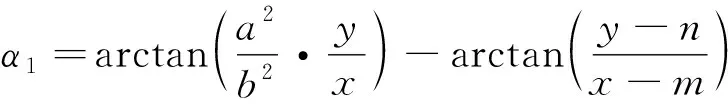
(2)

式中：(,)为椭圆管路承载点的坐标。

椭圆管路任意螺旋截面切线的垂线和椭圆管路中心与椭圆管路任意螺旋截面的连线的夹角∠，记为：

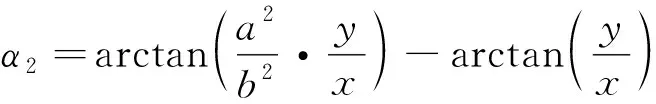
(3)

椭圆管路在承载点受到轴向外力作用的情况下，任意螺旋截面所受弯矩和扭矩为

=|sin|

(4)

=|cos|

(5)

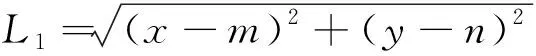
椭圆管路在中心点受到轴向外力作用的情况下，任意螺旋截面所受弯矩和扭矩为

=|sin|

(6)

=|cos|

(7)

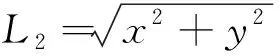
1.2 管路轴向刚度

刚度作为一种固有属性，在螺旋结构的构型参数与材料都确定后，其数值不会随外力大小和位置的不同而改变，外力只会影响螺旋结构的应力分布。因此，本文所研究的偏置拉压椭圆螺旋管路轴向刚度问题可等效为中心拉压椭圆螺旋管路轴向刚度问题，而偏置拉压的条件可在下节推导管路应力数学表达式时再引入。

本文采用能量法与微元法对椭圆螺旋管路轴向刚度的表达式进行推导。螺旋管路在进行拉压时，功能转换关系可表示为

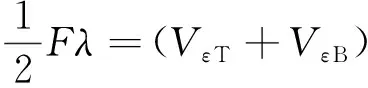
(8)

式中：为螺旋管路在轴向外力作用下的轴向变形长度；和分别为螺旋管路在轴向外力作用下的扭应变能和弯应变能。

采用微元法推导T和B。其中，对于扭应变能T：

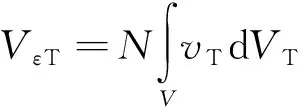
(9)

式中：为螺旋管路有效圈数；为螺旋管路单圈体积；为扭应变能密度；d为扭微元体积。

扭应变能密度可由材料力学推得：

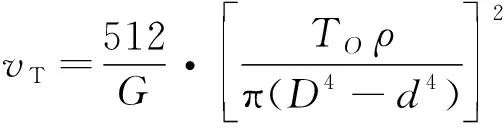
(10)

式中：为材料的切变模量；为微元距管路截面圆心的距离；为管路内径。

图5所示为管路螺旋截面微元示意图。对于扭微元体积d，结合图4和图5可得到以下关系：

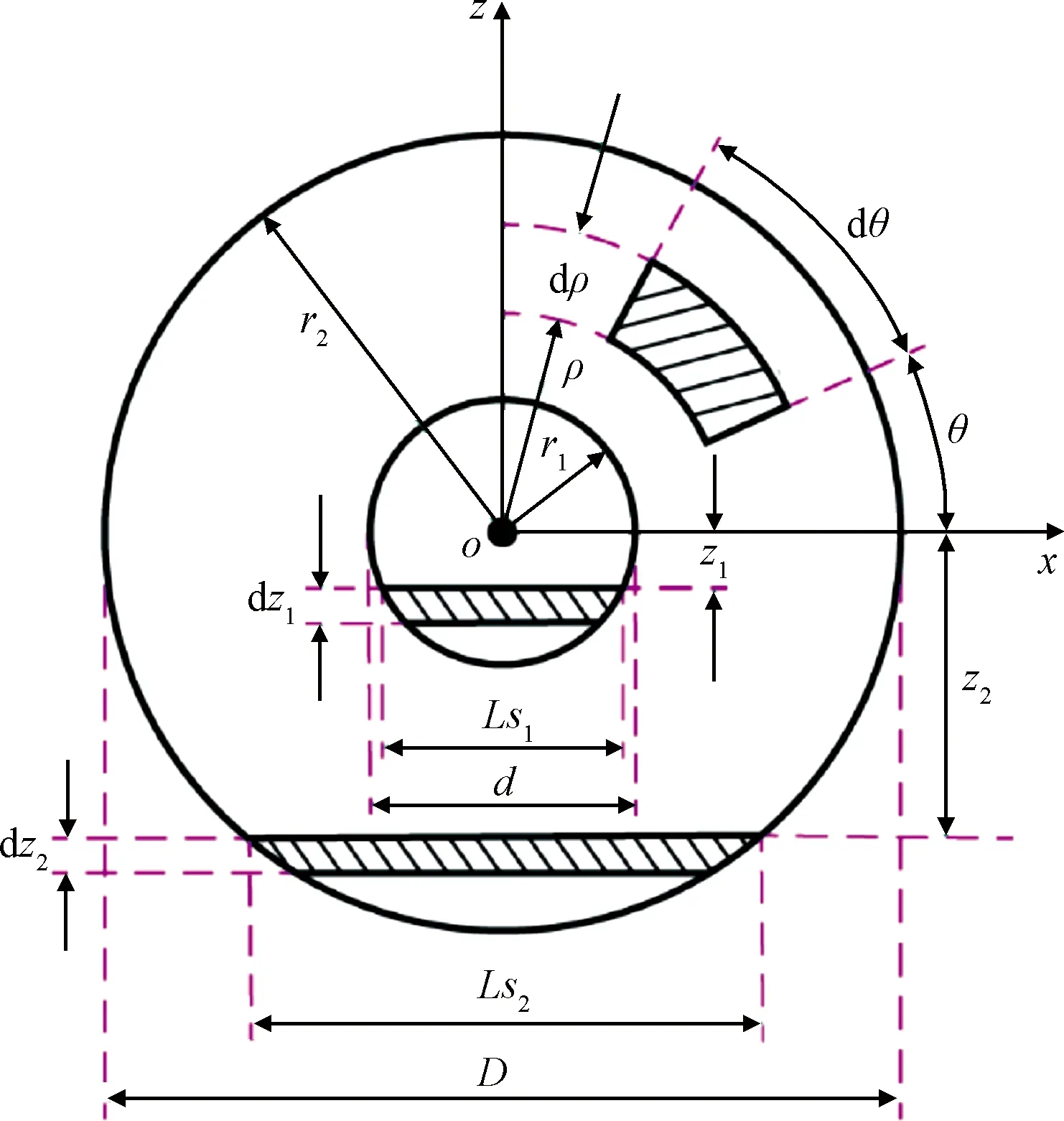
图5 管路螺旋截面微元Fig.5 Infinitesimal of the helical section of an helical pipeline

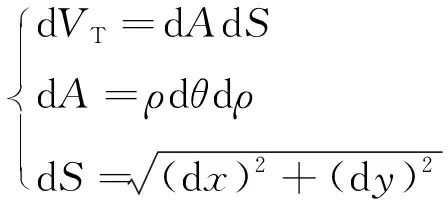
(11)

式中：d为微元面积；d为微元长度；d为微元夹角；d为扭微元宽度。

联立式(1)和(9)～(11)，扭应变能T可表示为

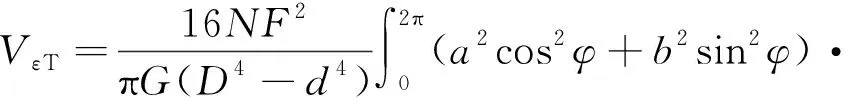
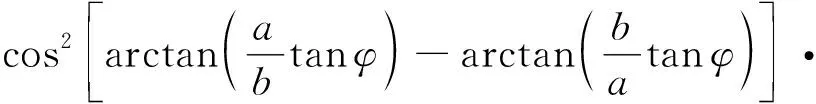
(12)

利用三角函数关系

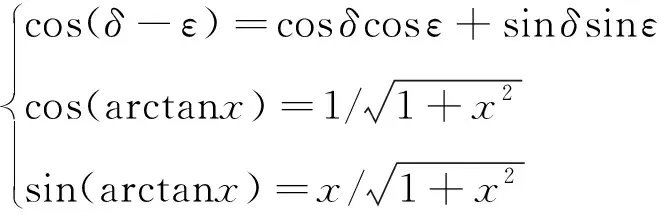
(13)

与函数的对称性，对式(12)进行化简，得到扭应变能T的简化表达式：

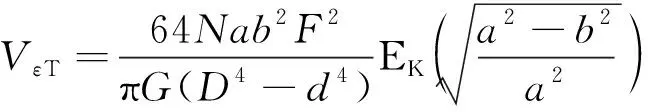
(14)

式中：E为第一类完全椭圆积分函数。

同理，对于弯应变能B：

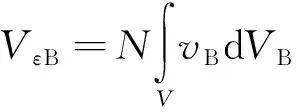
(15)

式中：为弯应变能密度；d为弯微元体积。

弯应变能密度可由材料力学推得：

(16)

式中：为材料的弹性模量；为管路螺旋截面上任意弦距截面圆心的距离。

对于弯微元体积d，结合图4和图5可得到以下关系：

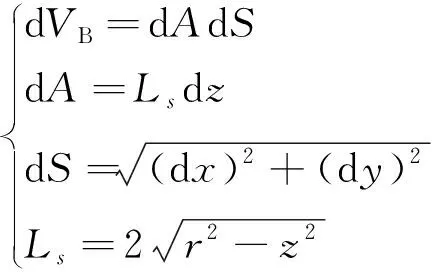
(17)

式中：d为弯微元宽度；为微元弦长；为管路半径，其中：为管路内半径，为管路外半径。

联立式(1)和(15)～(17)，弯应变能B可表示为

(18)

式中：

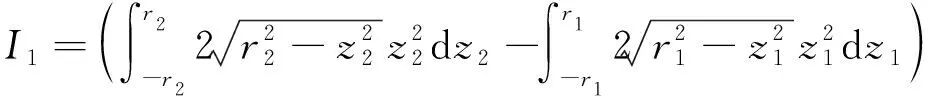
(19)

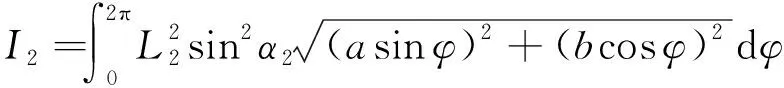
(20)

对式(19)进行化简，令=cos，化简结果如下：

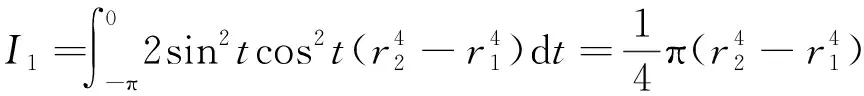
(21)

对式(20)进行化简，化简策略同式(12)～(14)，化简结果如下：

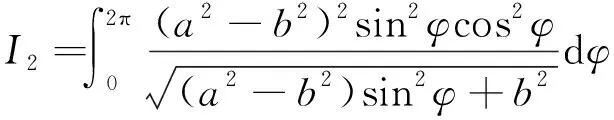
(22)

之后，结合分部积分法和直接化简法两种方法对式(22)进行进一步化简，最终可表示为

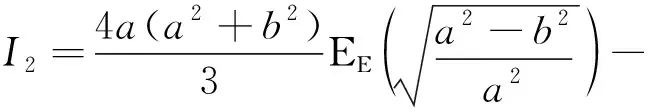
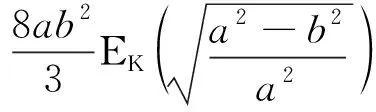
(23)

式中：E为第二类完全椭圆积分函数。

将式(21)和式(23)代入式(18)，得到椭圆螺旋管路弯应变能：

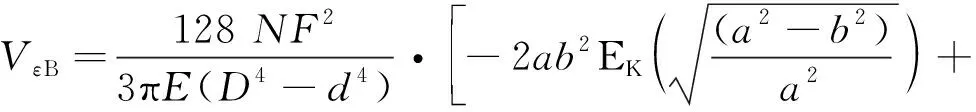
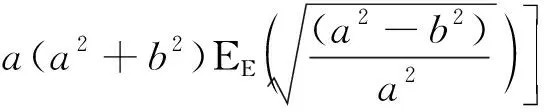
(24)

将式(14)和式(24)代入式(8)，得到椭圆螺旋管路轴向刚度：

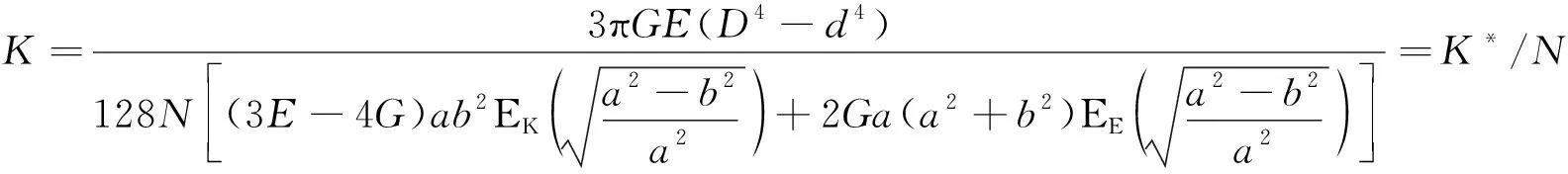
(25)

式中：为椭圆螺旋管路的单圈轴向刚度。

当管路为圆形包络即==时，式(25)退化为

=(-)(64)

(26)

式中：为管路俯视平面圆形包络的中径半径。

1.3 管路应力校核

采用第三强度理论推导偏置椭圆管路的应力数学表达式，用于校核管路的最大应力，避免塑性变形与断裂。第三强度理论如下式所示：

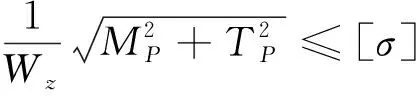
(27)

式中：为抗弯截面系数；[σ]为材料的许用应力。

将式(4)和式(5)代入式(27)，化简应力校核关系：

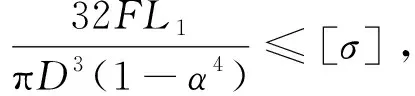
(28)

当管路的构型参数及轴向刚度确定后，只有的距离为变量。因此，管路的应力校核问题被转变为求最大值()的问题，即：

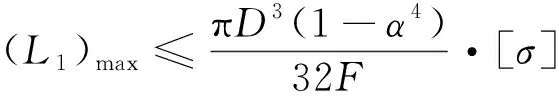
(29)

联立式(1)和，对()进行求导并令导数为0：

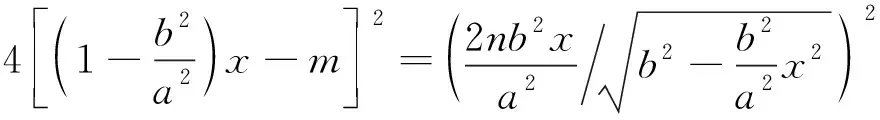
(30)

即可得到()对应的点(,)。

将(,)代入得到()，再将()代回式(29)，即可完成管路的应力校核。

2 仿真与实验校验

本节通过仿真与实验两种方式对偏置椭圆螺旋管路的轴向刚度数学表达式(式(25))及应力数学表达式(式(29))进行校验，管路参数见表1。

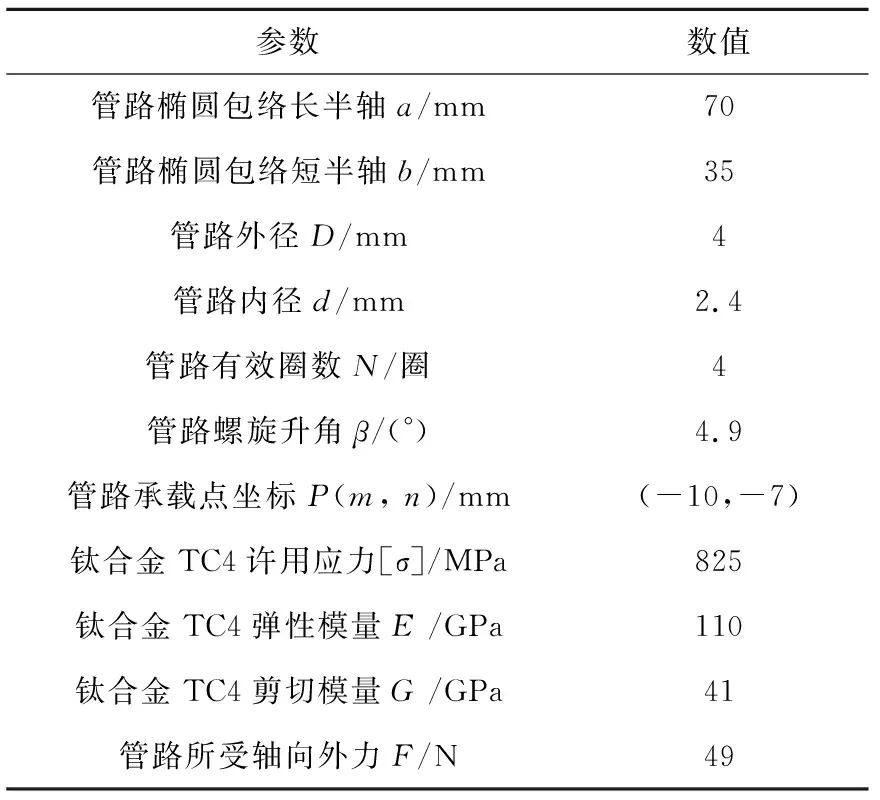
表1 偏置椭圆螺旋管路参数Table 1 Parameters of the numerical validation model of the bias-loading elliptical-helical pipeline

管路材料采用钛合金TC4，坐标系定义如图4所示。

将表1参数分别代入式(25)和式(29)，得到该管路轴向刚度与最大应力的数学结果：

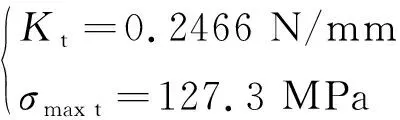
(31)

式中：σ为管路在轴向外力作用下的最大应力；下标t表示数学结果。

2.1 仿真校验轴向刚度及最大应力

通过有限元仿真校验管路轴向刚度及最大应力数学结果即式(31)的准确性。

根据表1参数在三维建模软件INVENTOR中创建管路的三维模型，之后将模型导入有限元分析软件ABAQUS中构建管路的有限元模型，分析管路的轴向变形(刚度)和最大应力，如图6所示。其中，管路的尾端点施加固定约束，前端偏置承载点处受到一个方向沿、大小为49 N的拉力。

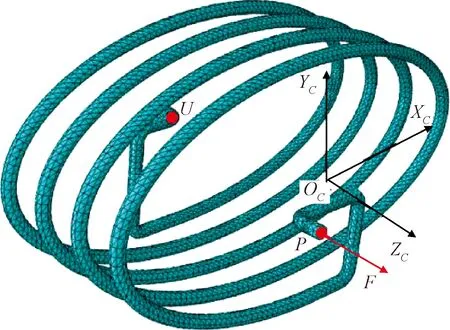
图6 管路有限元模型Fig.6 Finite element model of the pipeline

对仿真模型进行网格无关性分析：当有限元数量为最初的24159时，管路轴向刚度=37.4 mm，最大应力=118.2 MPa。之后逐步增加有限元数量，仿真结果会向某一定值逼近。当有限元数量增加至167334时，仿真结果已经趋于稳定，由有限元数量带来的结果误差已可以忽略不计，所得结果即可视为仿真真值，如下式所示：

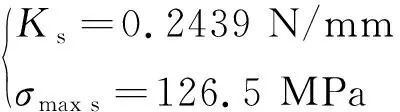
(32)

其中,下标s表示仿真结果。

2.2 实验校验轴向刚度

通过实验校验管路轴向刚度数学结果即式(31)与仿真结果即式(32)的准确性。

实验系统主要由加注管路、砝码、气浮直线导轨及基座组成，如图7所示。基座固定在实验台上，管路的尾端固定在基座上，管路的承载点与气浮直线导轨通过连接件固定，砝码加载在管路承载点处，通过测量管路轴向变形来得到管路轴向刚度的实验结果。其中，气浮直线导轨中“直线导轨”的作用是提供运动约束及抵抗偏置管路在拉伸过程中所产生的横向力，从而使管路沿管路轴线方向运动；“气浮”的作用是降低由横向力产生的摩擦力，尽可能地将原理误差降到最低。实验管路的参数同数学及仿真管路的参数一致，具体见表1。实验结果如下：

图7 管路轴向刚度实验系统Fig.7 Experiment system for testing axial stiffness of the pipeline

=02579 N/mm

(33)

其中,下标e表示实验结果。

将数学结果、仿真结果及实验结果进行汇总，具体见表2。其中，相对误差定义如下：

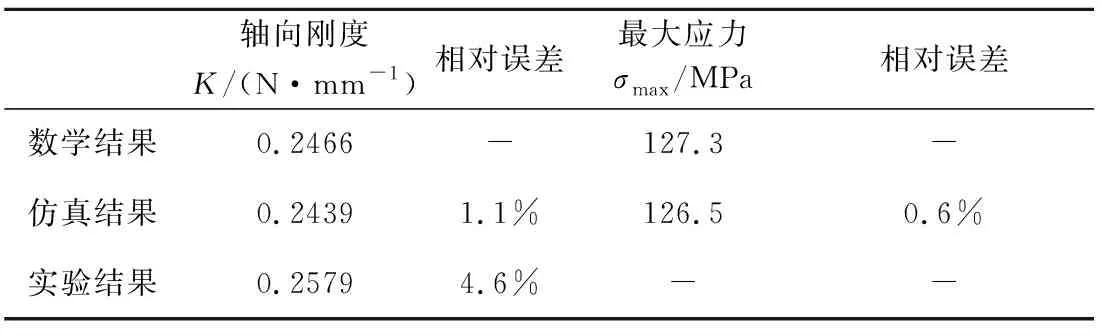
表2 偏置椭圆管路的数学、仿真和实验结果Table 2 Theoretical, simulation and experimental results of the bias-loading elliptical-helical pipeline

由表2可见,偏置椭圆螺旋管路轴向刚度的相对误差小于4.6%，最大应力相对误差小于0.6%，验证了轴向刚度数学表达式(式(25))和应力数学表达式(式(29))的准确性，可作为该类管路的理论设计工具。

3 在轨加注管路构型优化设计

针对在轨加注管路设计空间的紧凑性和附加力问题，偏置椭圆螺旋管路构型有着进一步降低附加力的潜力。本节将以某在轨加注对接机构为例，对非规则设计空间下的偏置椭圆螺旋管路进行构型优化设计，以形成一套完整的在轨加注椭圆螺旋管路设计方法；并将偏置椭圆螺旋管路同无偏圆、无偏椭圆以及偏置圆螺旋管路的最优构型进行对比，以验证偏置椭圆螺旋加注管路的优越性。

3.1 设计空间

对于在轨加注对接机构，无论加注管路的设计空间是否规则，都可简化为由两个矩形区域组成的组合区域。以本文作者设计的一种在轨加注对接机构为例，管路设计空间及相关定义如图8所示。其中，五角星点为管路前端承载点，圆点为管路中心点，虚线为管路设计空间边界，承载点是基于对接机构主体部分的设计而被动决定的已知点，设计空间被横竖两条点划线划分为,以及三个区域，加注管路的设计需要在设计空间内进行。绝对坐标系建立在设计空间上，局部坐标系建立在管路上。对于绝对坐标系：点为坐标系原点；管路前端承载点的坐标为(,)；管路中心点的坐标为(,)；为椭圆长半轴与轴的夹角。对于局部坐标系：点为坐标系原点；管路前端承载点的坐标为(,)，即管路承载点与中心点的偏置量。

图8 某在轨对接加注机构的加注管路设计空间Fig.8 Design space of the refueling pipeline for an on-orbit docking refueling mechanism

3.2 优化模型

本文的优化问题旨在对偏置椭圆螺旋加注管路的构型及位置参数进行设计。首先，根据管路极限压缩状态与原长状态下的几何约束关系，优化得到管路有效圈数的最大值；之后，在满足管路包络包含于设计空间内、工作状态下管路最大应力小于材料许用应力以及偏置管路附加力矩小于许用设计力矩的约束条件下，优化得到轴向刚度最小的管路参数。优化模型如下：

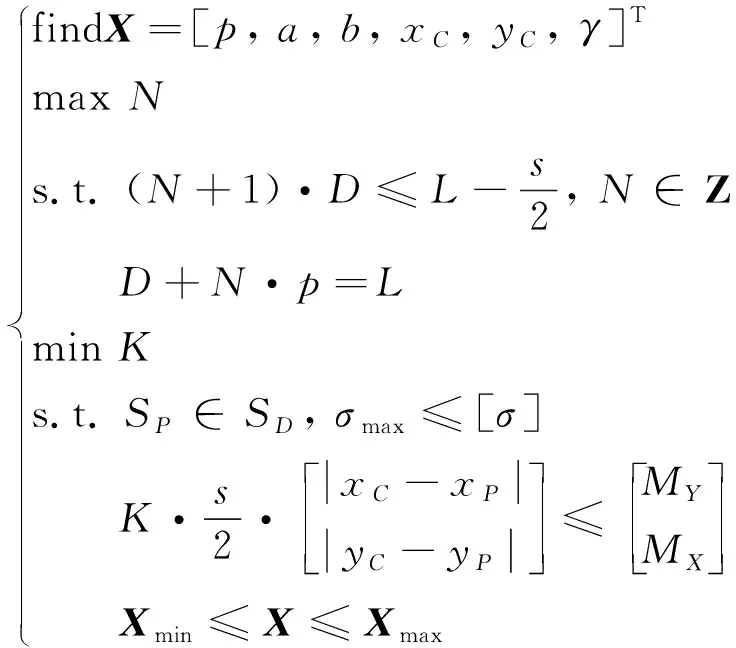
(34)

式中：为设计变量，其取值范围如图3和图8所示；为管路包络；为管路设计空间；为偏航方向许用设计力矩；为俯仰方向许用设计力矩。

之后，将优化结果代入式(35)计算得到管路的螺旋升角，从而得到管路的全部设计参数。

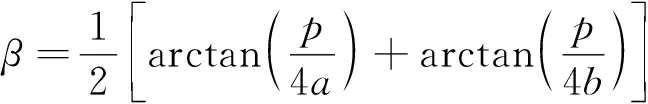
(35)

3.3 约束条件

对于(+1)·≤-2和+·=的约束条件，即管路几何关系，可由图3(b)得到；对于≤[]的约束条件，即管路应力校核关系，可由式(29)得到；对于·2·|()-()|≤()的约束条件，即管路附加力矩关系，可由图8(b)得到。

对于∈的约束条件，即管路包络需包含于设计空间内，其判断策略如下：

通过计算管路包络与各边界的交点数量来约束优化。最优的管路构型需同时满足以下条件：

(1) 不能与轴有交点；

(2) 不能与轴有交点；

(3) 不能与=，即上边界有交点；

(4) 不能与=，即右边界有交点；

(5) 必须与=有交点，即必须与=相切(1个交点)或者横跨区域或区域(2个交点)，且交点纵坐标和均位于区域。

(6) 必须与=有交点，即必须与=相切(1个交点)或者横跨区域或区域(2个交点)，且交点横坐标和均位于区域。

椭圆管路的一般方程可表示为

+++++=0

(36)

式中：,,,,,均为椭圆方程参数。

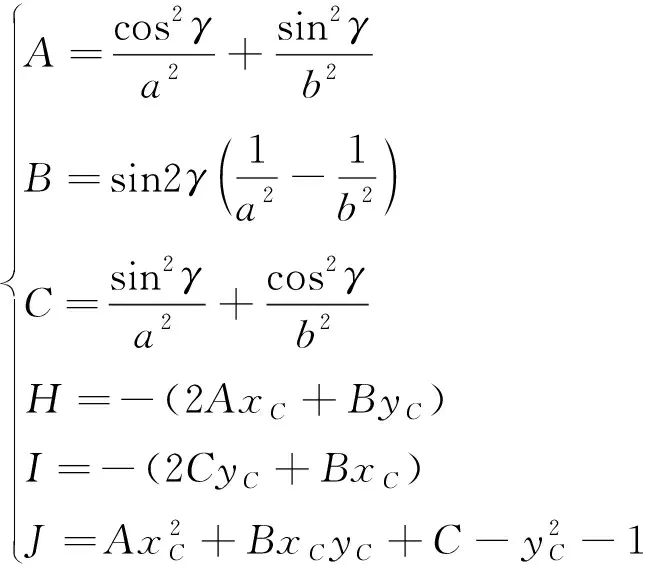
(37)

结合图8和式(36)，条件①～⑥可表示为

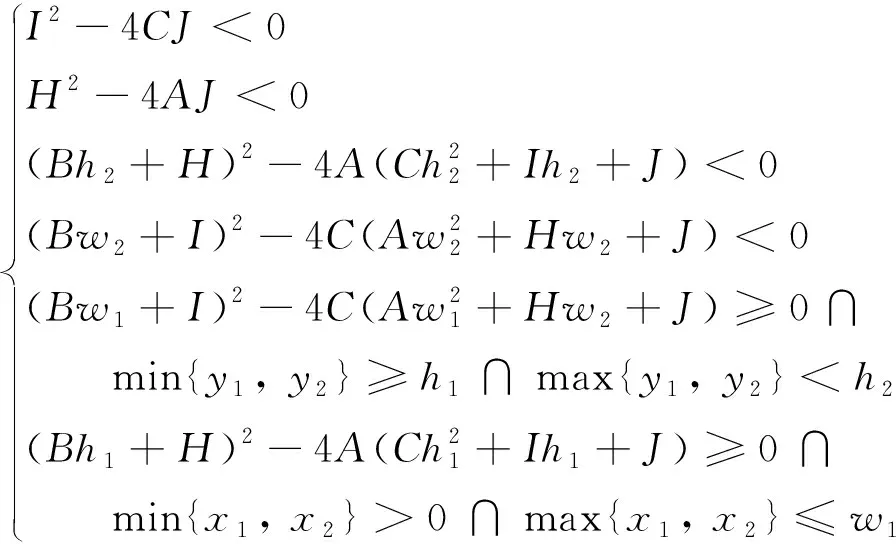
(38)

3.4 优化算法

对于本文的六维非线性约束工程优化问题，KRG-CDE是解决该类问题较为先进的算法。基于上述算法，本文所研究的在轨加注椭圆螺旋管路的构型优化设计流程如图9所示：首先采用序列二次规划算法(Sequential quadratic programming, SQP)对管路的有效圈数进行最大值优化；再基于有效圈数的优化结果采用KRG-CDE对加注管路的轴向刚度进行最小值优化。

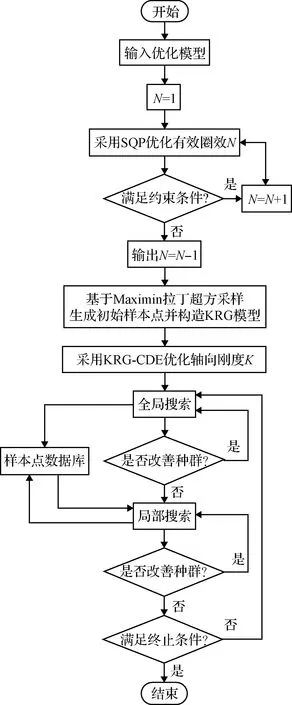
图9 加注管路优化设计流程图Fig.9 Flowchart of optimal design for refueling pipeline

KRG-CDE是一种基于克里金代理模型的全局进化算法。对于复杂工程问题，引入代理模型可以大大提高优化效率。KRG-CDE所采用的克里金代理模型的综合性能和其他代理模型相比具有明显优势。同时，进化算法可以充分探索设计空间，在不需要目标函数梯度信息的条件下快速高效的求解优化问题。KRG-CDE分为全局搜索与局部搜索两个阶段：在全局探索阶段，通过代理模型提供的预测方差，建立基于约束改善度与最优适应度的可行准则，引导种群向样本较为稀疏的可能存在最优解的区域进化。在局部搜索阶段，采用径向基函数构造局部优化模型并结合SQP求解，平衡了代理模型的鲁棒性、近似精度与构造效率，提高了算法的收敛速度。算法的具体细节可参见文献[24]。

3.5 优化结果与讨论

本节将结合图8(b)和式(34)～(38)，基于优化流程图9对某在轨加注对接机构的加注管路进行构型优化设计，相关参数见表1和表3。

表3 优化算例相关参数Table 3 Relevant parameters of the optimization example

在同一设计空间下，对无偏圆螺旋管路、偏置圆螺旋管路、无偏椭圆螺旋管路和偏置椭圆螺旋管路这四种管路分别进行优化，得到各自的最优构型(轴向刚度最小)。优化结果如表4和图10所示：

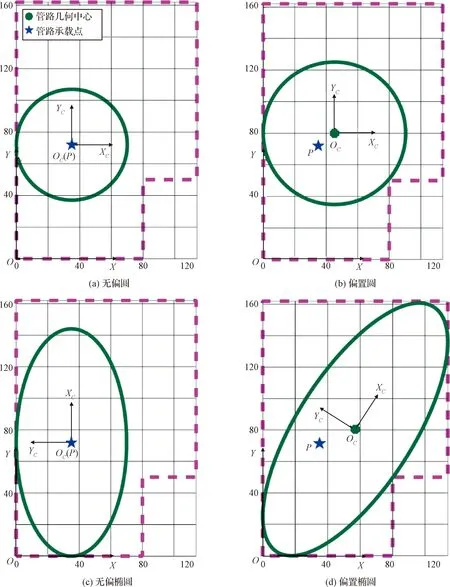
图10 四种加注管路的最优构型Fig.10 Optimal configurations of four types of refueling pipelines

表4 优化算例结果Table 4 Results of the optimization example

由表4可见,同一设计空间下，偏置椭圆螺旋管路的最优构型拥有最小的轴向刚度和最大应力。与常规无偏圆螺旋管路的最优构型相比，偏置椭圆螺旋管路的附加力降低了83.5%，最大应力降低了47.1%，并且也都优于另两种衍生构型，满足在轨加注对接机构对于加注管路附加力更小的设计需求。

4 结 论

本文针对在轨伸出式靠泊加注任务对接过程中加注管路因同步外伸而产生附加力的问题，提出了一种偏置椭圆螺旋构型的加注管路。首先基于能量法-微元法和第三强度理论推导了偏置拉压椭圆螺旋加注管路的轴向刚度与应力数学表达式。之后通过仿真与实验校验了数学表达式的准确性，相对误差均小于5%，可作为该类管路的理论设计工具。最后形成了一种在轨加注椭圆螺旋管路设计方法，并以某在轨加注对接机构为例，基于KRG-CDE对四种潜在的最优加注管路构型进行了最小轴向刚度优化设计。结果表明：偏置椭圆螺旋管路与常规无偏圆螺旋管路相比，其附加力降低了83.5%，最大应力降低了47.1%，更适用于伸出式靠泊加注任务。