基于深度强化学习的复杂地形适应机器人设计与实验
2022-10-15杨顿,杨帅,于洋,王琪
杨 顿,杨 帅,于 洋,王 琪
(北京航空航天大学航空科学与工程学院,北京 100191)
0 引 言
行星表面附着探测、地震废墟救援、天然洞穴探索等具有非结构化表面、变尺度缝隙、狭小空间和未知信息的环境探索任务,通常需要机器人具备地形适应力强、利用本体信息感知环境、可自主运动决策的能力。常规的足式机器人,如双足、四足、六足机器人,相较轮式机器人具有良好的运动能力,且感知、决策、驱动功能集成度高,但该类机器人结构尺寸相对固定,缺乏灵活性,难以适应行星、洞穴、废墟等极端地形下探索任务的部署和运输需求;同时,该类机器人一般使用基于模型的控制方法,需要尽可能多地利用传感器感知环境、估计状态,所建立的动态模型较复杂且泛化能力不足,这也将消耗不必要的计算资源和电力。
从仿生角度出发,借鉴自然界中动植物适应极端环境时所采用结构外形和运动模式,为以上问题提供了新的解决方案。在戈壁和海滩等地表复杂地形中,有两类生物——“风滚草”和海胆,可借助近似球体结构,利用滚动运动克服地形障碍,而海胆由于其可伸缩足腿而具备更强的自主适应性——主动避开或越过障碍,最终到达目标地点。以上述生物为灵感,NASA提出了一种仿风滚草行星探测器,可依靠火星风力驱动,实现星表探索,但不具备自主控制能力;Gheorghe等第一次提出了一种类似海胆的球形机器人,其利用球体内的伸缩机构推动机器人运动;日本东京大学的研究者研制的一款具有32条可伸缩足腿的球形机器人,基于运动学方法实现了直线和曲线的连续运动模式;MIT的研究人员设计了一种高伸缩比制动器,将其应用于14足仿海胆机器人的足腿机构,并制作样机验证了机器人在平面地形的基本运动能力。以上仿海胆机器人在结构设计上具备较好地形适应潜力,但目前还没有研究工作实现该类机器人的自主运动控制。
鲁棒且泛化性能良好的运动决策算法是实现自主运动的关键。由于这类机器人是非线性欠驱动系统,其步态控制是一项极具挑战性的工作。传统的足式机器人步态控制方法需要进行简化模型、状态估计、轨迹优化、足端位置规划、操作空间控制等一系列复杂步骤,尽管该方法可发挥机器人良好的机动性,但其通用性和泛化能力不足,需借助大量的专业领域知识,缺乏对变化较大的应用场景的适应性,较小的地形差异和传感误差就可能造成控制不稳定。自然界中,动物的运动技能是不断与环境交互试错而习得的。与此类似,强化学习就是这种不依赖机器人的运动学和动力学模型,通过训练提升决策能力的端到端数据驱动方法。但对足式机器人进行运动步态的强化学习需要处理连续高维状态空间和动作空间,计算量巨大。近年来,随着深度学习技术日趋成熟,结合深度神经网络的强化学习方法突破了连续高维空间计算量的限制,在诸多领域中取得了优于传统方法的效果,Peng等使用分层强化学习算法实现了仿真环境中的机器人运动方案,Kumar等实现了真实环境下的基于本体感知的四足机器人强化学习步态控制,Siekmann等实现了盲双足机器人在真实环境下的步态控制。然而,对于硬件系统研究尚未成熟的新型仿生欠驱动机器人,无先验知识的端到端运动策略训练和样机部署仍具有挑战性。
本文主要研究面向行星表面复杂地形探索任务的轻量化地形适应机器人解决方案,需要指出,所涉及的复杂地形指非结构化、无全局地形感知(视觉或雷达)信息的一类地形,其轮廓线的随机起伏可达本文机器人结构尺寸的70%左右;地形适应指该机器人能够稳定运动以躲避或越过此地形下的障碍、随机外部干扰,最终穿越地形到达运动目标。本文贡献包括仿生结构设计开发和基于学习方法的运动策略。首先,在分析海胆结构特点和运动原理的基础上,设计了一种新型仿海胆结构的十二足球形机器人(以下称“仿海胆机器人”),该机器人具有机构伸展率高、能耗低、无倾覆等优势。此外,还提出了一种基于无模型强化学习技术的高效步态训练算法。通过仿真实验验证了该机器人可实现平面地形下的近似周期性运动、非结构地形中基于纯本体感知的自主稳定运动,并可到达运动目标;同时对外部干扰具有鲁棒性。最后通过样机实验验证了算法所生成步态的动力学可行性。
1 结构设计方案
1.1 仿生结构分析及运动条件
如图1(a)所示,风滚草在风力驱动下可产生地形适应运动,但缺少驱动机构使其无法主动控制,只能被动翻滚。海胆依靠伸缩棘刺调整结构重心,可实现主动运动,但其运动方式以蠕动为主,速度较慢。两类生物近似球体的对称构型为稳定运动提供了基础,可伸缩足腿进一步加强了主动控制能力。结合以上生物机理,本文采用足腿对称分布的球形机器人结构方案,伸缩足作为驱动机构,可在复杂环境下实现整机构型的大幅变化,获得地形适应能力;以重心移出支撑三角形而发生翻滚作为运动方式,可简化步态的设计难度。结构设计细节需要考虑以下几类特征:

图1 运动原理及结构设计Fig.1 Motion principle and structure design
(1)对称性:高度对称是该机器人能以简单运动方式适应复杂地形的基本条件。然而实物样机受限于机电和结构性能,无法实现与海胆相近的足腿数,因此为保障结构对称,本文将足设置在正多面体的顶点和面心,以确保其足腿呈中心对称分布。
(2)足腿数量:考虑到机器人足数、整机质量和驱动能力之间存在相关性,合适的足数对高效完成运动目标具有重要影响:一方面,足数较少会减小足与支撑面夹角,降低触地足与地面的摩擦,增加打滑的可能,且需要更大的电机推力;另一方面,足数较多,运动所需电机推力将变小,但会增加整机重量和控制复杂度。综合考虑结构质量和设计生产难度,本文选择了十二条可伸缩足,其由正十二面体基座和驱动机构组成,通过控制每个驱动机构的径向运动,可实现整机形状改变以适应地形。
(3)足腿伸缩长度条件:机器人足数和位置确定后,需考虑伸缩足的最小伸缩长度。如图1(b)所示,机器人用三条足腿支撑站立时,其中一条为驱动腿,另外两条为支撑腿。假设机器人的运动从图1(b)所示的位置开始,驱动腿伸长使重心投影移出轴之外,机器人可实现一步翻滚动作。已知正十二面体的二面角(相邻两个平面的夹角)约为11656°。因此机器人两条腿之间的角度近似为6344°。图1(b)中代表驱动腿初始长度,Δ代表驱动腿伸长量。是驱动腿与两条支撑腿,形成的平面的夹角,则存在如下伸缩关系:

(1)
可以得出约为58.28°,将,代入公式,得到Δ≈062,即最大伸长量达到原长的1.62倍及以上才可实现翻滚。结合样机制作过程的其他影响因素,机器人样机最终采用1.68倍伸缩比方案。
1.2 结构设计
综合考虑结构特点和运动条件,整机结构设计如图1(c)左图所示。执行机构安装在正十二面体的基座面心上。执行机构末端设计为球形触地壳,保证其与地面发生点接触,便于进行摩擦力分析。
(1)驱动机构:驱动器应满足轻质、可径向运动的要求。本文自主设计了一款电动直线执行器。单个执行机构由步进电机和套筒组成,包括电机、进给螺杆、滑台、支架。套筒与滑台固连,随着进给螺杆的转动而产生径向运动。作为滑台的外延,套筒尺寸通过步进电机直径确定,需在满足结构要求的同时尽量减小直径,同时保证不降低机构伸缩比。
(2)基座:为使执行机构伸缩比满足运动条件,要尽可能减小基座直径,并增大中空体积,用于放置硬件控制系统。
(3)传感器:作为自主运动机器人的外界感知来源,机器人十二条足腿末端装配有接触力传感,中心基座装配惯性传感器,同时关节的位置和速度信息可获取。以上感知将作为运动策略的输入状态。
1.3 初代样机平台制作
如图1(c)右图所示,整体包括执行机构、基座和控制系统。基座和套筒使用3D打印。硬件控制系统包括一个Arduino 2560控制板和4988步进电机驱动模块。部件具体材料及尺寸见表1。将步态数据输入Arduino控制板,输出电脉冲信号;A4988驱动模块接收电脉冲信号,并驱动执行机构达到期望长度。初代样机用于开环步态验证,未搭载额外传感装置。样机总质量大约为700 g。

表1 机器人材料及尺寸Table 1 Robot material and size
2 基于强化学习方法的数据高效步态训练算法
在使用传统方法进行仿生足式机器人的步态设计和运动控制时,需要已知的地形信息,进而建立精确的系统模型进行反馈控制,以实现稳定运动。这一方法缺乏对非结构化未知地形的适应能力。因此,本文采用基于数据的强化学习方法,使用从状态空间映射到动作空间的深度神经网络作为机器人运动策略,控制其在仅具备本体感知的非结构化环境中自主运动。
本方法首先需在仿真环境中进行模型训练,待策略网络收敛后,将其迁移到真实环境中具有感知能力的样机上,开展自主运动实验。
作为一类构型新颖的机器人,为避免从头设计运动模式、规划步态,同时为了发挥数据驱动方法和翻滚运动模式的优势,本文采用从0到1的训练模式,即基于无模型、无先验知识的训练方案,仅通过奖励函数为神经网络的优化提供引导。该方法具备更强的通用性,可根据不同的任务目标和地形条件快速训练不同运动策略。无模型强化学习方法的困难之处在于训练数据量过大、任务繁重。为此,本文利用机器人翻滚式运动的特点,设计了一种高效的数据采样方案。经过短时间训练即可实现仿海胆机器人在多种复杂地形的自主决策运动。
2.1 策略熵最大化强化学习
仿海胆机器人在未知环境下的运动控制过程可以由参数组{,,,,}所描述的部分可观马尔可夫决策过程(POMDP)抽象为强化学习问题,其中,表示状态空间和动作空间;表示状态转移矩阵;是机器人与环境交互时得到的奖励回报;是表示未来奖励的衰减因子,取值范围是[0,1]。强化学习的核心目标是学习出一种从状态空间映射到动作空间的策略,以从环境中获得最大的累计回报:
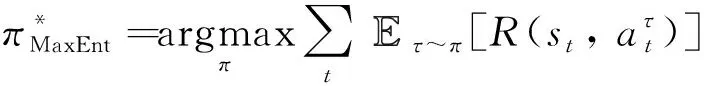
(2)
式中:表示数据采样时间步;表示从策略中采样出的轨迹。传统的强化学习算法仅实现奖励函数的最大化,由该方法得到的运动策略在同一状态下会采用相同的动作,运动模式较为单一。但面向复杂地形探索任务的足式机器人需要具备同一状态下采取多种可能动作方式的能力,才能完成对障碍地形的探索和克服。所以在优化网络时引入了对策略网络熵的优化指标:
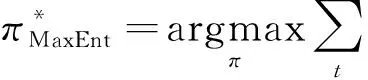
((·|))]
(3)
同时最大化奖励和熵可保证机器人在完成任务目标获得奖励的同时,策略具备较强的探索能力。
2.2 强化学习算法设定
网络结构主要由两部分组成:动作值函数Q网络和策略网络(Policy),参数设置如表2所示。策略网络输出层的作用是输入观测状态后,输出12个关节的初始动作值。初始动作值经过映射算法得到关节可执行的伸缩长度。

表2 网络结构及参数设置Table 2 Network structure and parameter setting
可观测状态选取
本文设计的海胆机器人对环境信息的感知基于本体传感器,不依靠视觉、雷达、地图等高维观测数据。获取感知信息的硬件是惯性测量单元、步进电机和足端的接触力传感器。因此,可观测状态主要选择以上三方面信息,包括:十二个伸缩关节的位置和速度:{,…,,,…,};中心基座的速度和姿态角:{,,,,,};触地腿信号{,…,}。对以上42个观测值进行归一化处理后,作为Policy网络和Q网络的输入。
动作空间
观测状态信息经过策略网络的传递和处理后,在输出端得到十二维高斯分布函数,对此分布进行抽样,可得到一组初始动作值。若直接以此初始动作值作为机器人关节运动量,实验发现机器人将发生剧烈的碰撞和弹跳,无法部署到样机上。因此本文对网络输出值Action设计了映射算法进行约束,约束后的机器人在实验中可以以最接近样机真实的运动方式运行,算法流程如图2所示。

图2 网络输出-关节动作映射算法流程Fig.2 Flow chart of the network output and joint motion mapping
奖励函数设置
强化学习方法的优势是可通过简单的奖励函数为机器人设定复杂运动目标,而不用设计者熟练掌握某一领域的特定知识,本文设置如下奖励函数:

(4)
式中:

为训练机器人具备沿直线运动能力,仿真时,在某一时间步下,将坐标的变化量作为主要奖励,持续向轴正方向运动获得正奖励;方向的速度(当前质心在坐标方向下的速度与前一时间步的速度之差)越大将得到越高奖励;奖励函数对于少于三条触地腿的情况进行惩罚,其中表示落地腿数目;奖励限制了能量消耗,指第条腿的关节伸缩量。以上4项为衡量机器人运动状态的基本奖励,总奖励为各奖励之和:

(5)
对于特定任务目标还可补充特殊奖励。由此可以得到最终的奖励函数形式:
=+
(6)
2.3 高效数据采样方案及训练框架
传统强化学习算法在马尔可夫决策过程中会按照时间顺序对仿真过程的序列数据依次采样。但翻滚式机器人在运动时具备特殊性质:当质心投影点移出支撑三角形后,此时不用再施加关节动作量,翻滚动作即可自然发生,并在一段时间的持续定轴转动后稳定到下一姿态。这段转动时间随机器人结构、姿态、重力加速度的不同会有差异,如果对这一性质加以利用,即将传统方法对每一时间步依次采样的过程改变为按照转动时间间隔进行采样,则可使用更少的数据训练出更高效的翻滚技能。
在实验中对转动时间间隔参数进行了参数搜索,最优参数在同一任务下相较依次采样方法训练速度提升5倍以上,具体可参考实验部分3.2节。基于以上方法和环境设定,利用图3所示的框架进行策略网络的训练,具体分为两个并行循环:循环一是机器人与环境交互,产生新的马尔可夫序列数据;循环二是存储数据并优化网络参数,提升网络性能。

图3 运动策略网络训练框架Fig.3 Movement policy network training framework
3 实验及分析
3.1 仿真验证实验
仿真实验在动力学开源平台Pybullet 3.0.7上进行,运算主机配备了英特尔i7-8500U处理器和16 GB内存。神经网络使用基于CPU版本Pytorch框架进行训练,机器人模型参数设置如表3所示。

表3 仿真实验参数设置Table 3 Simulation experiment parameter setting
平面地形实验:首先在该实验中进行运动策略可行性验证,预设5000回合训练,每回合进行200时间步的探索,同时在此环境中补充如下奖励函数:

(7)
该奖励限制了机器人在方向的位移,使其以接近直线的轨迹朝轴正向运动。训练目标是以最低能耗平稳地运动进入目标地点,同时尽量保持3条腿触地,以减少落地撞击。经过5小时训练,机器人达到了目标平均奖励,学习曲线及运动效果如图4,5(a)所示,代表仿真中的实时时间。

图4 平面地形学习曲线Fig.4 Flat terrain movement learning curve
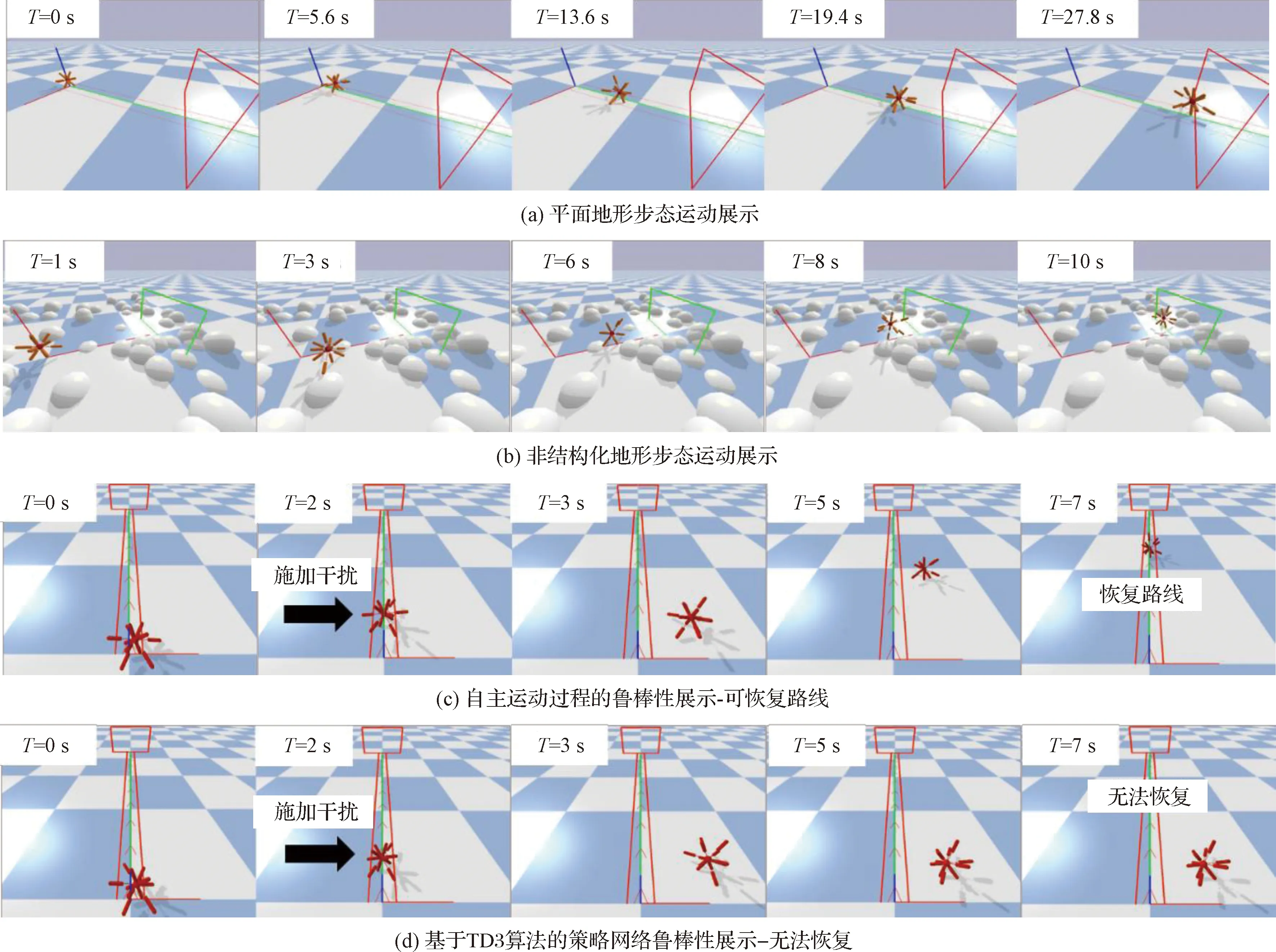
图5 多地形运动步态,自主运动过程的鲁棒性展示及对比Fig.5 Multi terrain gait movement display, demonstration and comparison of robustness of autonomous motion process
非结构化地形实验:非结构体现为位置和数量随机生成的石块障碍,如图6(a)所示,石块的直径在0~280 mm之间,机器人所有关节全伸长状态下尺寸为320 mm;训练时,机器人只能通过自身足端接触、关节长度、速度和中心姿态感知外界,因此该相对比例下的未知复杂地形对机器人而言具有较大挑战性。
非结构化地形训练实验预设12000回合,每回合进行1000时间步探索。训练目标是在复杂环境中机器人通过网络进行自主运动控制和决策,越过障碍进入目标地点。经过20 h训练,学习曲线基本收敛,如图6(b)所示,运动展示如图5(b)所示。
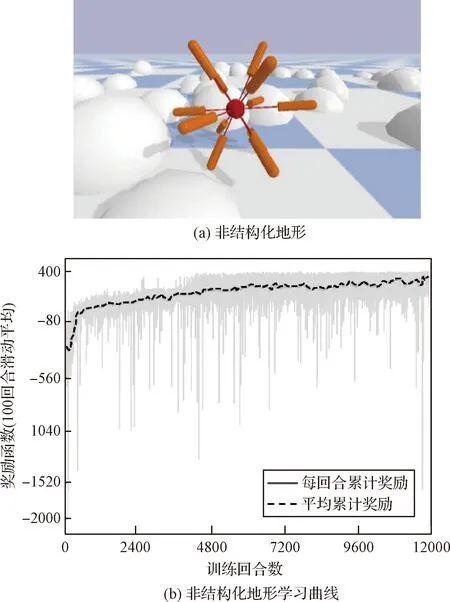
图6 非结构化地形及训练曲线Fig.6 Unstructured terrain and learning curve
鲁棒性实验:本文通过对搭载训练过的策略网络的机器人自主运动过程施加较大外力干扰,发现其具有较强鲁棒性,即在外力干扰下偏离目标轨迹后,撤除外力,机器人会自主调节运动过程,直至恢复目标轨迹,如图5(c)所示。
3.2 对比实验
为验证基于翻滚运动模式设计的数据高效采样方案对步态训练的影响,进行了对比实验。实验发现最优时间间隔参数为45。图7对比了参数为30,45,80时的学习曲线,参数45相较参数80的训练效率提升2倍以上,相较参数30效率提升5倍以上。
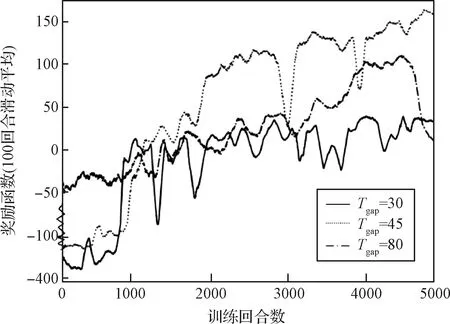
图7 不同时间间隔参数对训练效率的影响Fig.7 Effect of different time gap parameters on training efficiency
为验证引入了策略熵最大化指标的强化学习算法训练的策略能力,将该网络的鲁棒性与基于TD3强化学习算法的训练结果作对比。对比图5(c)和图5(d),对相同训练任务的运动过程施加较大外力干扰后,基于本文方法训练的智能体可自主恢复路线,基于TD3算法的智能体不能对环境干扰做出响应,最终无法自主恢复运动路线。
图8提取了机器人平面地形运动过程(35时间步),可看到该策略未基于任何先验信息而习得了近似周期性切换的步态,这一结果符合自然界翻滚式运动模式的步态特征;同时可发现在大多数时刻,机器人保持3腿着地状态,该状态下机器人质心运动平稳,但仍然存在某些时刻着地腿少于3的情况,在这一时刻,机器人的运动稳定性较差,质心处于较高点,可能会与地面发生剧烈撞击,这是需要进一步提升的方向。

图8 平面地形周期性步态切换序列、关节能量消耗、质心高度曲线和单足落地时刻Fig.8 Flat terrain periodic gait switching sequence, total energy consumption, centroid height curve and single foot landing time
3.3 样机实验及分析
为验证本文方法所训练的运动步态在实物样机平台上的可行性,本文提取了策略网络在平面地形下生成的步态数据,并在样机上进行了开环步态实验。如图9所示,该步态结果可实现摩擦接触较复杂平面下的稳定运动,运动过程基本保持3条腿触地情况。
图9(a)中0~30 s运动过程展示了一步翻滚动作,俯视图如图9(b)所示。初始时刻机器人保持三足支撑,当其准备翻滚至下一状态时,为避免落地冲击对样机造成破环,其训练得到的步态首先伸长前进方向上即将落地的新支撑腿(探测足)和此时已着地但下一时刻将腾空的支撑腿(驱动足),同时其他悬空足将以某种规律伸长或缩短以配置质心。如图9(a)中=11 s和图9(b)中时刻2所示,机器人将以缓慢稳定的过程以两支撑足触地点连线为轴旋转,直到质心越过两不动支撑足时,探测足触地,驱动足离地,全过程保持3条腿着地的方式完成本次翻滚。之后,探测足和驱动足将收缩达到新的稳定状态,以调配下一步翻滚的质心位置。

图9 平面地形开环步态样机实验Fig.9 Open loop gait prototype experiment on flat terrain
由样机实验过程可看出,相较手动设计步态,基于学习方法的步态结果具有更高的运动效率:在实现本次翻滚的质心调整时,部分关节的伸缩已开始为下一次翻滚动作准备,因此该方法可更大程度发挥多足机器人冗余自由度的结构优势。
4 结 论
针对适应性结构和智能化控制在行星表面轻型自主探测任务的需求,结合仿生思想和强化学习方法,本文设计了一种仿海胆结构的十二足球形探测机器人及基于SAC算法的步态训练策略。实验表明,通过高效训练,该机器人可快速掌握未知非结构化地形下的自主运动能力和抗干扰能力。在虚拟环境实验中:平面地形下,无模型策略习得了近似周期的步态序列;随机石块地形和施加外力情形下机器人均能自主躲避障碍、抵抗干扰、完成运动目标。同时,通过开展自研样机的实验,验证了数据驱动方法所生成的步态在真实环境下的动力学可行性。为进一步开展复杂地形测试提供了实验基础。与已有方法相比,该方法所生成的步态具有更高的鲁棒性和运动效率。
另外,本文提出的运动策略无需动力学模型或运动学模型等先验知识,具备不同地形下的泛化能力。机器人具有结构简单、无倾覆等优势;通过快速训练,即可直接部署;可为洞穴、沙漠等地球极端地形的自主探测,或新一代小行星表面探测器的设计提供参考。本文后续将进一步结合传感器融合技术,实现样机平台在真实环境探测场景下的高精度运动控制。
