脉冲展开式飞网质量分布与展开稳定性优化
2022-10-15竺伟梁庞兆君司骥跃杜忠华
竺伟梁,庞兆君,司骥跃,杜忠华,程 春
(1. 南京理工大学机械工程学院,南京 210094; 2. 北京机械设备研究所,北京 100854;3. 宁波大学冲击与安全工程教育部重点实验室,宁波 315211)
0 引 言
降低空间碎片带来的危害是航天界的共同愿望,清理空间碎片的空间绳网技术应运而生并得到了快速发展。作为新型的空间绳网技术之一,脉冲展开式飞网利用旋转离心力抑制绳网回弹,实现绳网在无控条件下持久保形,对加快空间碎片清理具有重要促进作用。由于绳网自身材料和结构特性,在发射后一段时间内网面的展开状态是不稳定的。脉冲展开式飞网发射展开到网面最大状态后将经历回弹-再展开的振荡阶段才能逐渐实现稳定。为便于表述,后文中将该阶段称为回弹振荡期;将回弹振荡期内网面从完全展开状态到回弹后最小展开状态的降幅称为最大回弹率。脉冲展开式飞网展开过程中最大回弹率越小、回弹振荡期越短则网面展开稳定性越高。因此,降低最大回弹率、缩短回弹振荡期对飞网稳定展开具有重要意义。
绳网优化是提升绳网展开性能的有效方法,根据优化对象可分为绳网发射参数优化、绳网结构优化和网面质量分布优化。其中,绳网发射参数优化相对成熟,通过优化发射速度、发射角度等提升绳网的展开性能。例如Zhang等设计了一种半解析的优化方法,基于简化的多柔性梁单元全动力学模型优化了绳网的发射参数以扩大绳网在指定位置的展开面积。高庆玉、Chen等基于kriging代理模型和MOEA/D-EGO耗时优化算法建立了空间绳网的多目标优化问题,以绳网发射速度、发射夹角和质量块质量为优化对象,优化提升了网面展开性能。绳网结构优化是一种较为新颖的绳网优化方法,其通过优化绳网结构来提升绳网的展开性能。司骥跃等采用移动可变形组件法构建了绳网结构优化模型,并用遗传算法对绳网的构型进行整体优化,使得优化后绳网的有效展开位移提升36.18%。上述两种绳网优化方法在一定程度上能够提升网面的展开性能,但也存在一定局限性。绳网发射参数优化是初浅的,未能优化绳网自身的动力学特性。此外,该方法在实际应用中受工况约束影响较大。绳网结构优化则是一种相对深层的优化,通过优化网面自身的动力学特性以提升绳网展开性能。然而,网面结构优化前后网面结构和网面节点质量分布都发生了变化,难以清楚地界定优化指标提升的本质原因,也无法归纳得出一般规律。质量分布优化也是一种动力学特性优化,现有关于柔性体结构的质量分布优化问题多集中在柔性薄板和柔性伸展臂方面,在绳网动力学方面还没有学者开展相关研究。因此,网面质量分布优化是一种提升绳网展开稳定性的新颖方法。该方法以网面各节点层的质量为优化对象,建立网面各层质量分布规律,提升绳网的展开稳定性。相比于绳网结构优化,网面质量分布优化可归纳出各层节点质量分布对绳网展开稳定性的一般规律。
本文针对脉冲展开式飞网,基于多体系统传递矩阵法建立了网面质量分布模型,以缩短回弹振荡期和降低绳网回弹率为目标优化了网面的质量分布状态,提升了脉冲展开式飞网的展开稳定性。
1 绳网动力学建模与脉冲展开式飞网展开原理
1.1 绳网动力学模型
绳网动力学建模中,常用的方法有绝对节点坐标法、有限元法和集中质量法。其中集中质量法计算效率高、可移植性强,在绳网优化迭代方面具有较大优势。本文采用集中质量法,将一条连续的绳段离散成若干质量节点,相邻节点之间通过并联的无质量弹簧-阻尼单元互相连接,如图1所示。相邻节点间的力可表示为:
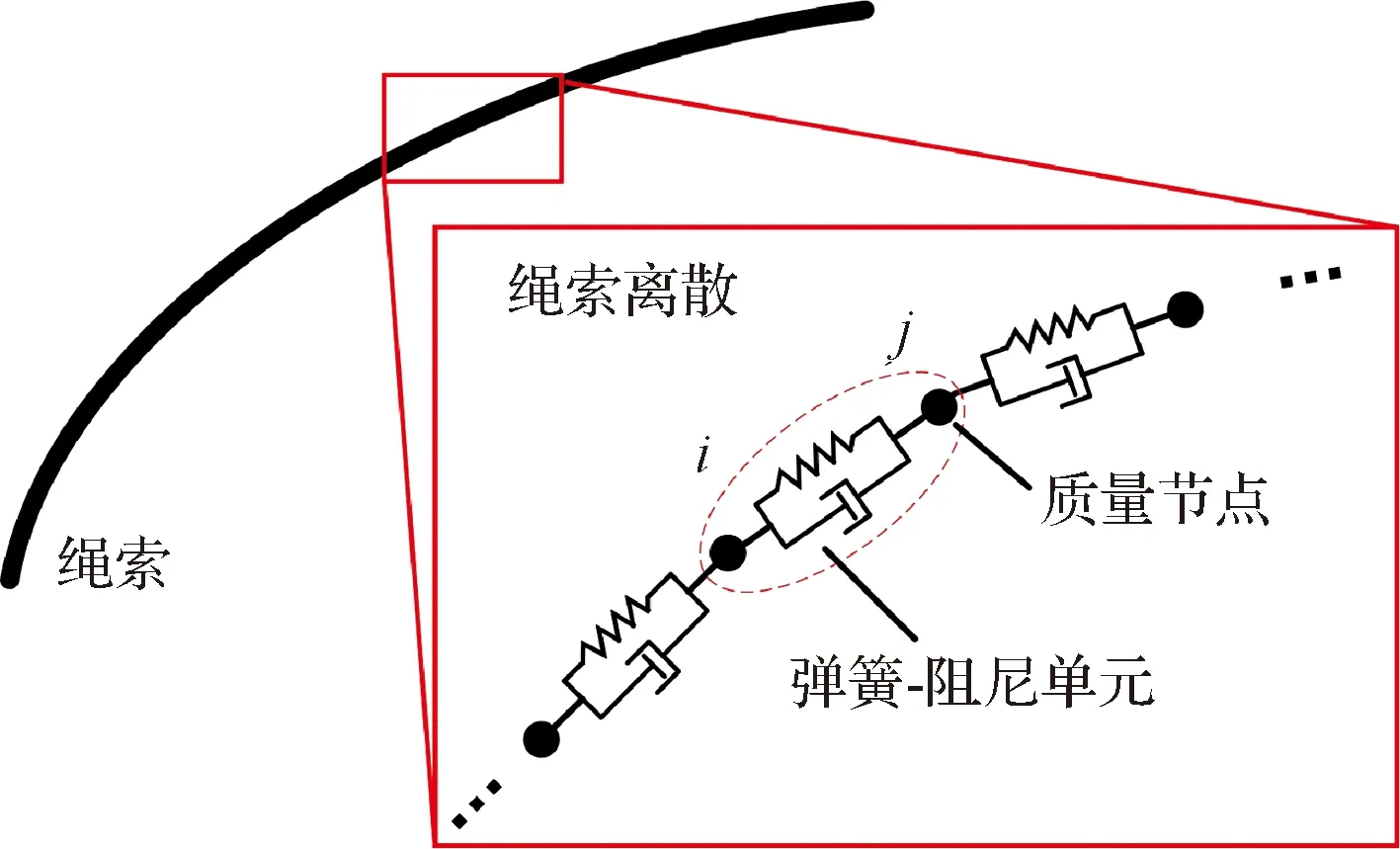
图1 质点-弹簧-阻尼模型Fig.1 Mass point-spring-damper model

(1)
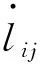
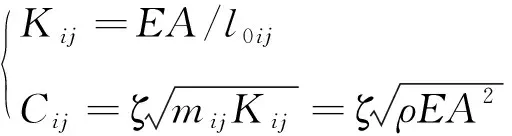
(2)
式中:为绳段的杨氏模量;是绳段的截面积;是阻尼比;是绳段的密度;是节点和之间的绳段质量。
进一步将绳网沿网面结点离散成若干质量节点和弹簧-阻尼单元,并用无向图=(,)进行表示,如图2所示。其中,顶点集={1,2,3,…,}代表绳网上离散的质量节点集,边集代表绳网上相邻节点之间的连接绳段集。网面上各节点之间的连接情况可由邻接矩阵()表述,其组成元素为,则绳网上节点的受力可表示为:

图2 绳网模型Fig.2 Net model

(3)
1.2 脉冲展开式飞网展开原理
脉冲展开式飞网是一种展开过程中利用单次脉冲实现持续保形的空间绳网,飞网展开过程可分为两个阶段:第一阶段为牵引体弹射阶段,牵引体以一定发射角度进行弹射并带动绳网在空中展开;第二阶段为单脉冲作用阶段,当飞网面积展开至60%后,牵引体产生切向脉冲力致使网面旋转,并利用旋转离心力实现持续保形,如图3所示。
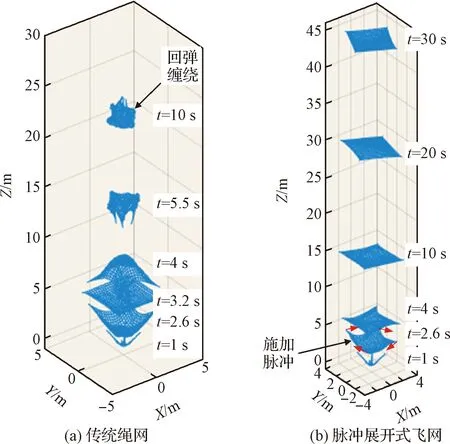
图3 传统绳网与脉冲展开式飞网展开过程对比Fig.3 Comparison of the unfolding process between the traditional net and the single-pulse-deployed net
相比于传统绳网展开,脉冲展开式飞网可避免回弹缠绕,并持续保持网面展开状态。然而,脉冲展开式飞网首次展开至最大值后将经历回弹-再展开的回弹振荡期,如图4所示。回弹振荡期内飞网展开状态不稳定、展开率波动较大将影响对目标的可靠抓捕。
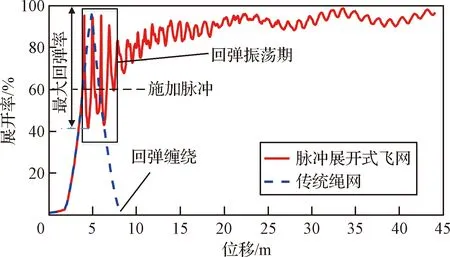
图4 传统绳网与脉冲展开式飞网的展开率对比Fig.4 Comparison of the unfolding ratio between the traditional net and the single-pulse-deployed net
优化网面的质量分布是一种理想的优化方式,从飞网自身动力学特性出发,调整网面质量分布以降低网面回弹率、提升网面展开稳定性。该方法无需调整绳网发射参数,因此对一些绳网发射条件严苛的工程具有更好的适应性。
2 质量分布模型
实际应用中,网面结构较大、网格数多、自由度大,难以直接对网面质量分布进行优化求解。此外,较多的网格数将导致质量分布优化问题中的优化变量过多,质量分布最优解的收敛效果难以保证。因此需根据绳网结构特性和网面质量分布规律建立网面质量分布优化模型,降低优化变量个数。
绳网由多个绳段相互连接组成,绳段的受力和运动特性与绳网的动力学特性有着较大的相似性。为便于理论推导,首先建立一维绳段模型,并推导质量分布对绳段拉伸和回弹问题的影响规律。随后将一维绳段的质量分布规律推广至脉冲展开式飞网,并建立网面质量分布模型,从而将多优化变量的网面质量分布问题转化为单一优化变量模型以提升多目标优化求解效率。
2.1 基于传递矩阵的一维绳段质量分布模型推导
多体系统传递矩阵法是一种高效的多体系统研究方法,在兵器、航空、航天等领域得到广泛应用。采用矩阵形式对离散的绳段模型进行表述,并通过矩阵累乘得到绳段的动力学传递矩阵。多体系统的响应可由模态主振动叠加而成,若某阶模态下多体系统的固有频率为,则对应的状态量可表述为:
=ei
(4)
式中:i为虚数单位;称为模态坐标下的状态量。
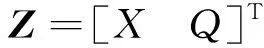
=-1
(5)
式中:表示第个物体。
绳段受外力拉伸扰动后,绳段的最大回弹量与其最大拉伸量成正相关,因此可选取绳段最大拉伸量作为观测对象。绳段受扰动后在短时间内即可达到最大拉伸状态,该过程中比例项起主导作用。为便于分析,在短时间内可略去阻尼项。因此,绳段模型可进一步简化为弹簧质点模型。对于一根两端自由且左右对称的一维绳段,在左右对称扰动下可构建一端固定、另一端自由的多体系统动力学模型,如图5所示。其中固定端代表绳段的中心点,模型中各离散节点质量分别为,,…,,∈{2,4,6,…,-2}。绳段的质量分布通过调节离散节点的质量实现。
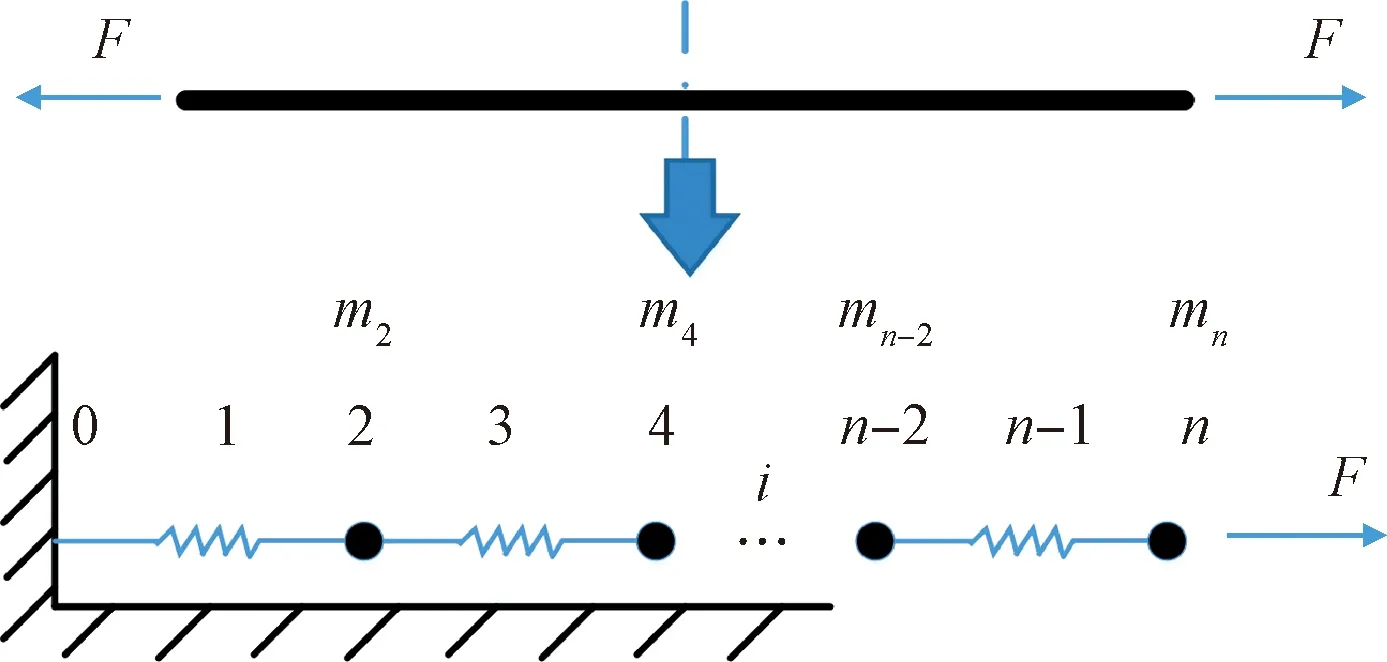
图5 绳段动力学模型Fig.5 Dynamical model of rope segment
将一个弹簧和一个节点视为一个单元,该单元的传递矩阵为:
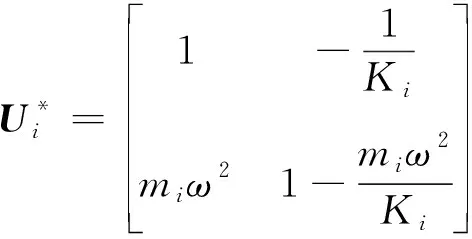
(6)
式中:为节点的质量;为系统的固有频率;为弹簧的弹性系数。
对于两个相邻的单元,其传递矩阵为:
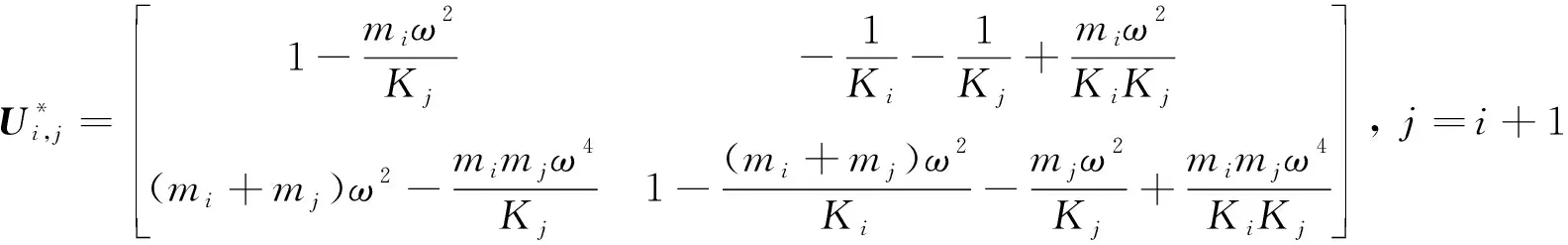
(7)

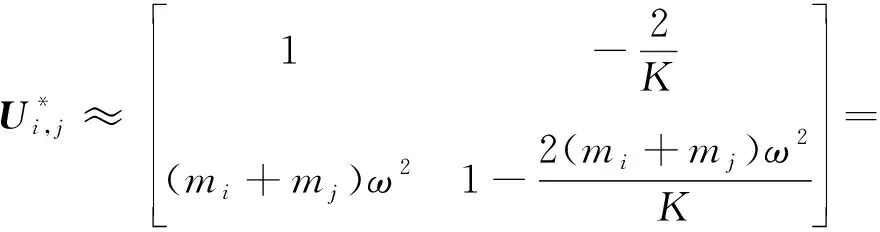
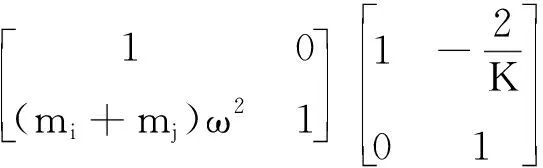
(8)

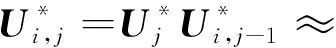

(9)
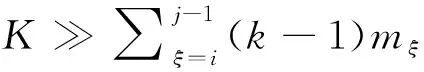

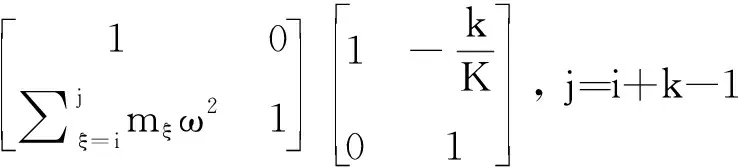
(10)


图6 等效邻接单元模型Fig.6 Equivalent model to adjacent element

(11)
在扰动力的作用下,链式系统的传递矩阵可增广至3×3的矩阵,对应的状态量也增广至3×1的列向量,如式(12)所示。
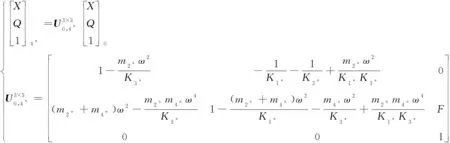
(12)

4=
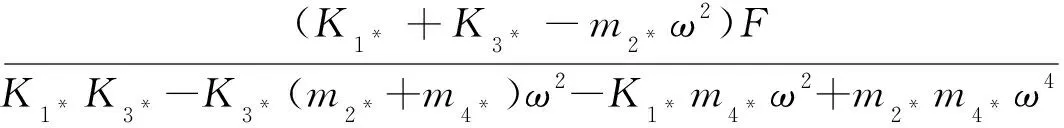
(13)
当1,3≫2,4,且min(1,3)>2时:

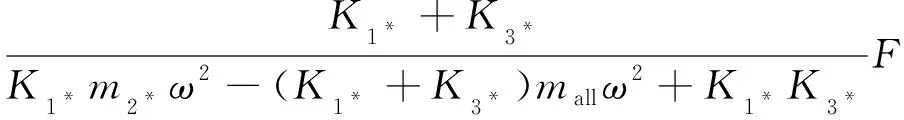
(14)
显然,4是关于2的近似反比例递减函数,即绳段的最大拉伸量是关于2的减函数。其中,=2+4为绳段的总质量。
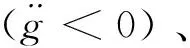
图7 三种绳段的质量分布函数Fig.7 Three mass distribution functions of the rope
为验证一维绳段模型推导结果的正确性,现基于MWorks和Matlab进行验证。设置8个串联的弹簧阻尼质点单元,为避免节点质量过小导致的积分误差,将绳段总质量分为两部分:一部分为各节点均分的基础质量,另一部分为质量分布规律决定的可变质量。具体参数设置详见表1。
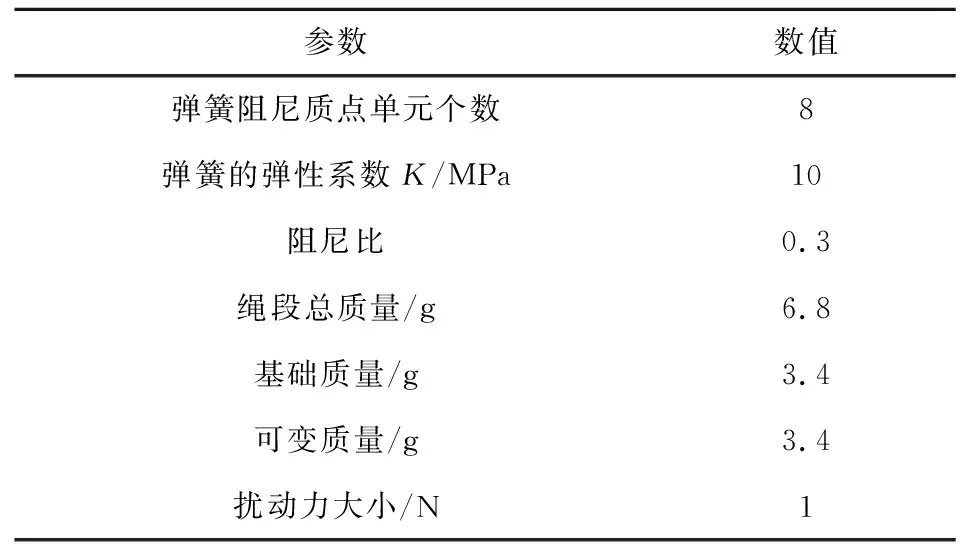
表1 仿真参数Table 1 Simulation parameters
分别建立线性递增、均匀分布、凸形递减、线性递减和凹形递减共5组质量分布,各组可变质量分布情况如图8所示。
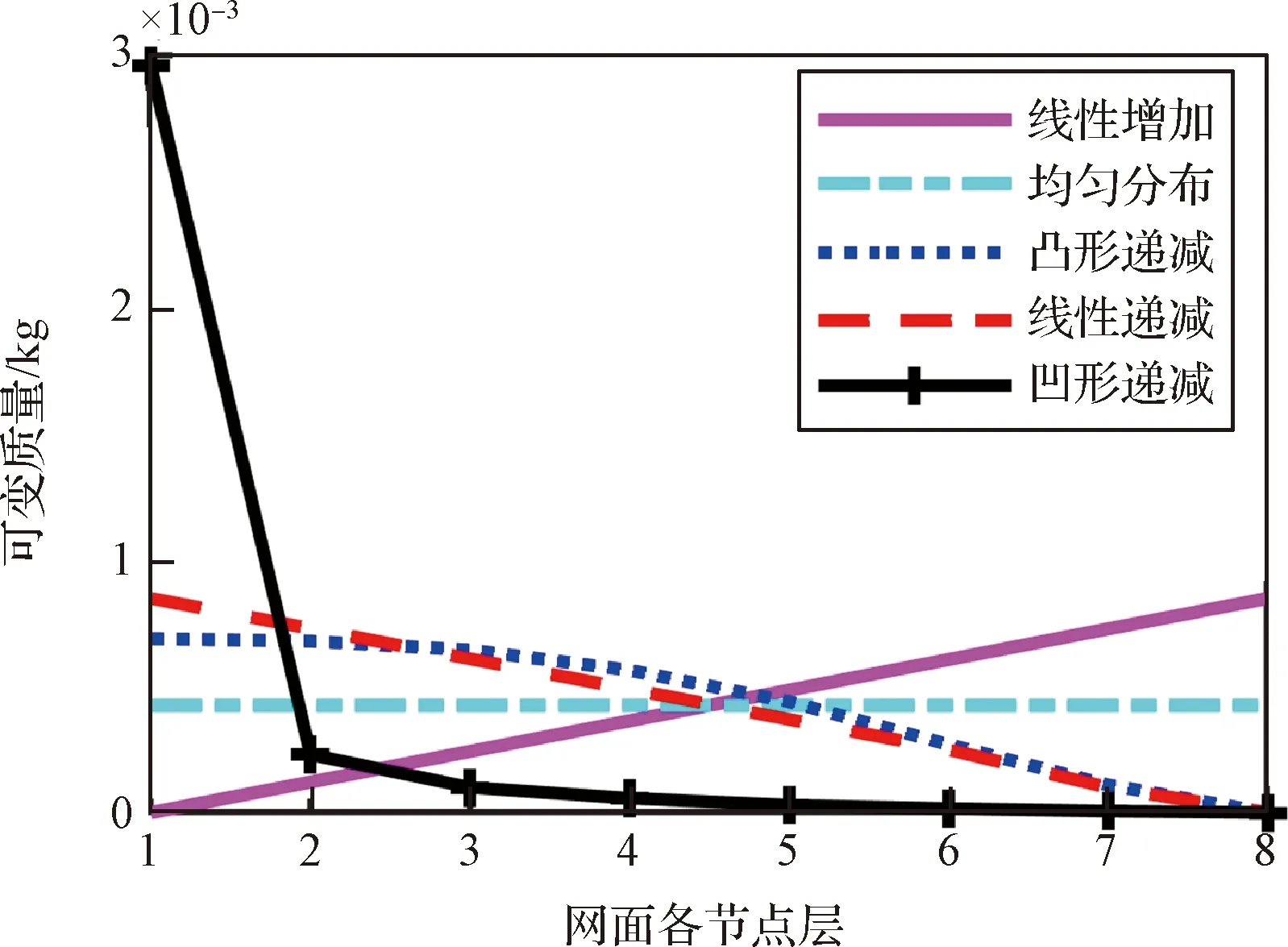
图8 5种质量分布中可变质量的分布Fig.8 Five distributions of assignable mass

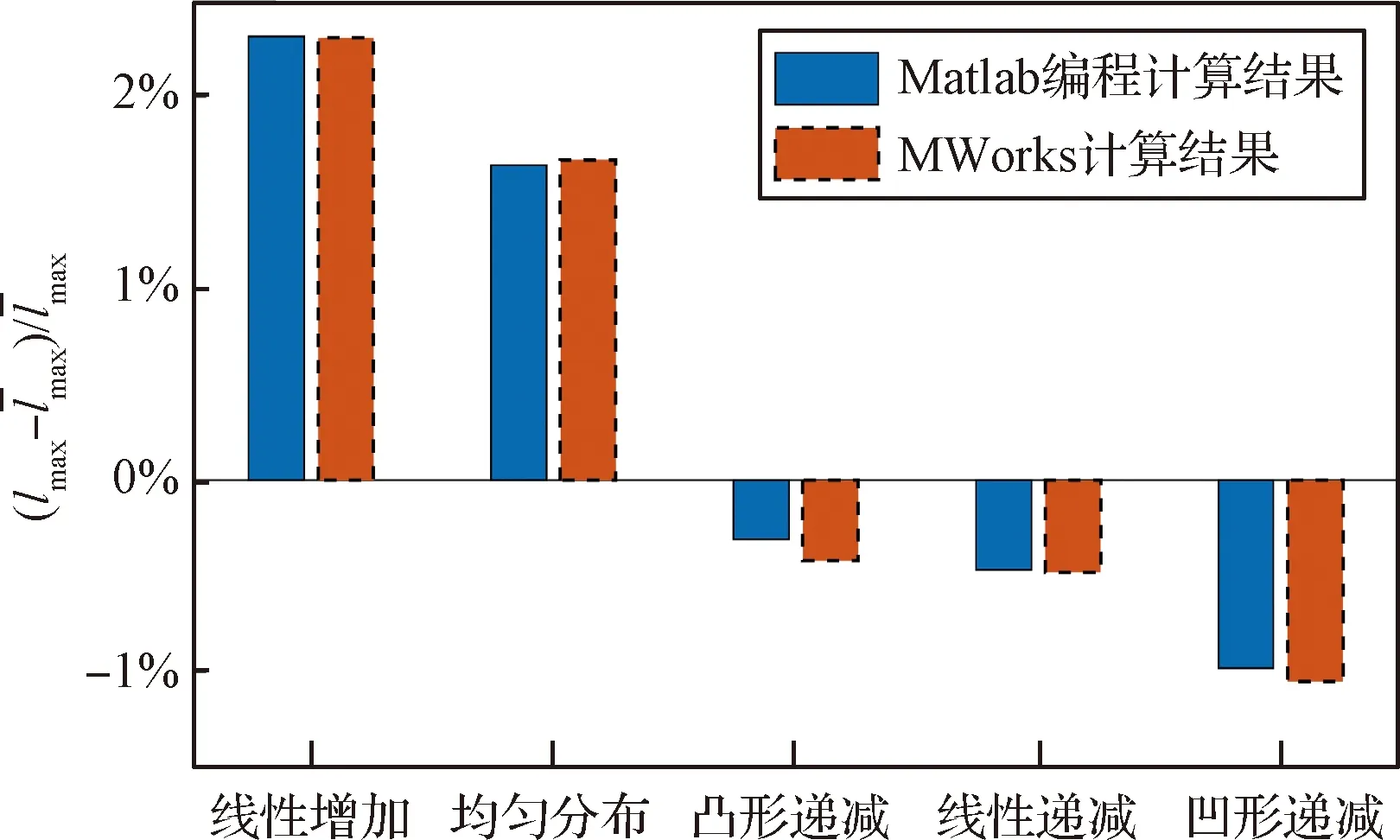
图9 不同质量分布下绳段的最大伸长量对比Fig.9 Comparison of maximum elongation of rope segments with different mass distributions
2.2 网面质量分布模型建立
绳网由若干绳段连接而成,具有类似绳段的运动特性。将绳段的质量分布规律拓展至二维绳网,并通过数值仿真验证网面质量分布规律。借鉴一维绳段模型,通过集中质量法将网面按照节点进行离散,并将节点从网面中心向边缘进行逐层划分,如图10所示。为避免节点质量过小导致的积分误差,将绳网的总质量划分为基础质量和可变质量两部分。在绳网总可变质量守恒条件下通过调节各层节点的可变质量实现网面质量分布调整。
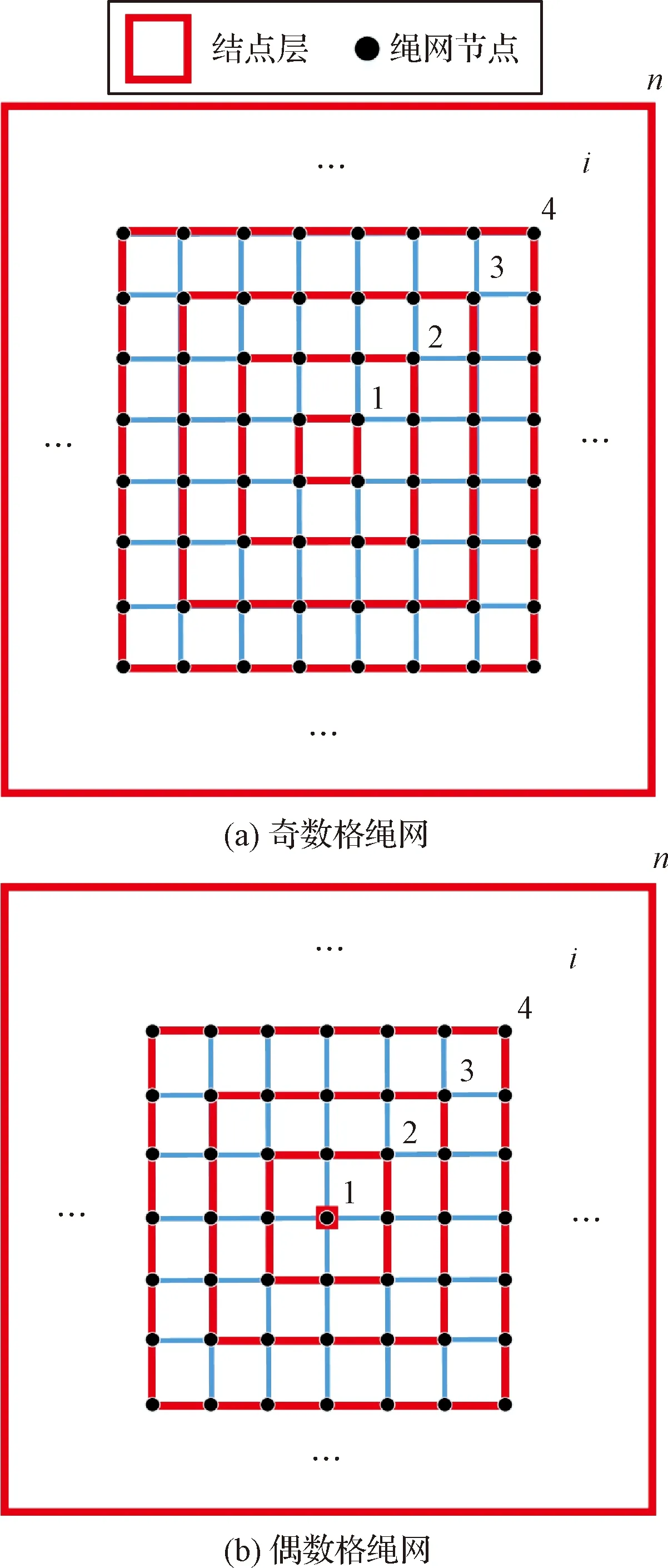
图10 绳网节点层Fig.10 Tiers of the mass-nodes upon the net
绳网各层节点数可表示为:

(15)
式中:∈。对于节点总层数为的绳网,第层的节点质量为()。任意两不同层的节点质量(),()为两个相互独立的变量。因此,节点总层数为的绳网优化变量个数为。结合式(15),绳网的可变总质量为:

(16)
不失一般性,以边长为5 m,单边15格的方形Kevlar绳网为例。从网面中心逐层向外,将网面各层节点质量按照线性递增、均匀分布、凸形递减、线性递减和凹形递减五种质量分布规律赋值,并保证绳网可变质量守恒,如表2所示。其中,绳网总质量为0.2448 kg,基础质量0.1224 kg,可变质量0.1224 kg。控制牵引体弹射速度为5 m/s,牵引体质量为350 g,发射偏角为30°,脉冲速度10 m/s,绳索的弹性模量为70 GPa,泊松比为0.3。
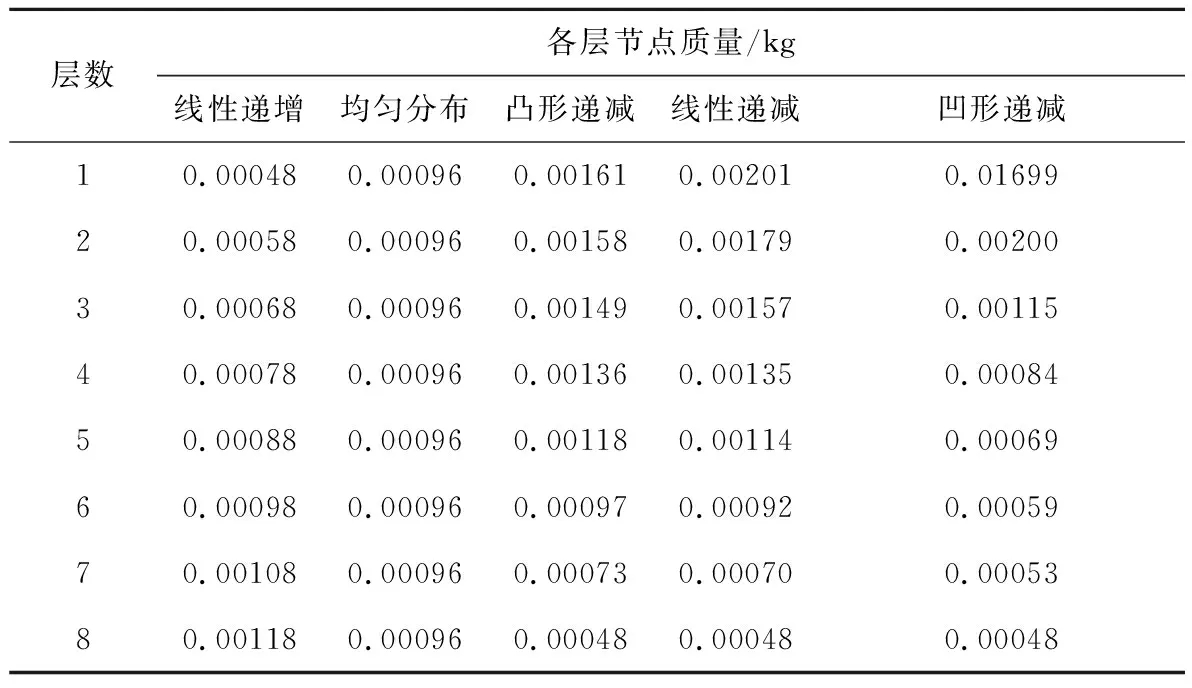
表2 五种网面质量分布规律Table 2 Five kind of net surface mass distribution models
五种网面质量分布规律对应的网面展开状态如图11所示。绳网质量分布对最大回弹率的影响规律基本与一维绳段问题中所得规律一致,在线性递增、均匀分布、凸形递减、线性递减和凹形递减五个网面质量分布规律中,凹形递减的质量分布规律所对应的网面展开最稳定。五种网面质量分布规律所对应的网面最大回弹率依次递减,分别为74.15%,67.50%,60.10%,58.23%,35.57%。

图11 五种质量分布状态下脉冲展开式飞网展开率对比Fig.11 Comparison of unfolding ratio of the single-pulse-deployed net under five mass distributions
基于网面节点分层特性,可将各层节点质量设为优化变量进行优化,对于节点总层数为的绳网则有个待优化的变量。实际工程中通常网面层数较多,导致绳网质量分布优化问题中优化变量过多,最优解难以快速收敛。因此,需要根据网面质量分布规律建立网面质量分布模型,降低绳网质量分布优化问题中优化变量的个数。由前文分析可知,凹形递减分布是一种较优的质量分布规律,故以此对网面质量分布模型进行探究。
第一象限内的反比例函数(-)+是一种典型的凹形递减函数,可通过调节增益、相位偏移量和常数项得到不同曲率的凹形递减函数。根据网面节点层号离散的特点,将反比例函数改写为离散形式,得到网面质量分布模型:

(17)
式中:为节点总层数;为节点层编号,根据对网面各层节点质量()进行赋值。为满足∀∈[1,],(,,,)≥0,需保证0<<1且(=,,,)≥0。此时,网面质量分布模型中未知自变量为,,。引入边界条件:(=,,,)=0,即有:
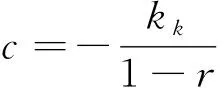
(18)
将式(15),式(16)代入式(18)得到:

(19)
对于给定可变总质量为和绳网节点总层数为的绳网,是关于相位偏移量的单值函数。故式(17)可进一步改写为:
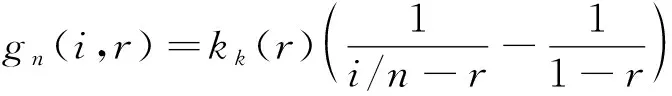
(20)
式中:∈(0,1)。此时,网面质量分布模型中未知自变量仅为相位偏移量。
3 脉冲展开式飞网多目标优化
脉冲展开式飞网展开过程中,以最大回弹率和网面回弹振荡期(数值上按照展开率均值稳定在95%以上所需的时间进行计算)为目标函数进行优化。
将网面质量分布模型和遗传算法相结合的优化方法(后称本文方法),仅需优化单一变量即可得到优化的网面质量分布结果。该多目标优化可表述为:
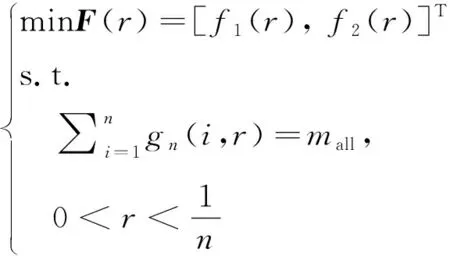
(21)
式中:()代表相位偏移量与目标函数集[,]之间的映射;()为关于参数的凹形递减质量分布函数;为绳网的可变总质量。
绳网多目标优化问题中,和之间具有冲突性,难以找到一个使得两目标函数均为最优的解。因此,采用Pareto非劣解对优化结果进行表述。以网面边长为5 m、单边15格的方向绳网(=8)为例,质量均匀分布为初始解进行多目标优化。
为对比本文质量分布模型下的多目标优化效果,设置对照组:根据网面节点分层特性,将每层的节点质量设置为优化变量,并采用遗传算法进行逐层优化,优化过程中优化变量总数为。对照组可表述为:
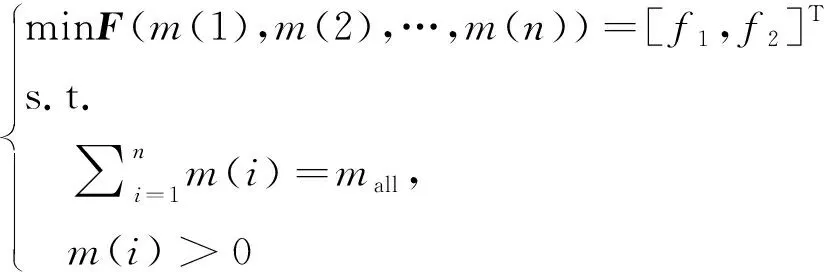
(22)
经多目标优化分别得到4组Pareto非劣解集,如图12所示。由于绳段单向受力特点导致的绳网动力学映射不连续性,使得遗传算法优化得到的Pareto非劣解呈集散状分布并伴随多个重叠的非劣解。图中点的位置代表目标函数的值,点的大小代表解的重叠度。在相同且较少的遗传代和种群数量条件下,本文方法能够更快地收敛得到更优的解;而对照组中,直接采用遗传算法对网面节点质量进行逐层优化的方法则需要更多遗传代和种群数量才能收敛得到较优解。

图12 边长为5 m,单边15格的方形绳网的Pareto解集Fig.12 Pareto solution set for a square rope net with side length 5 m and 15 grids on each side
本文方法优化后,飞网在7 s至9 s内恢复稳定状态,最大回弹率控制在29.5%以内。从初始解到较优解的提升是由网面质量分布模型实现的,提升幅度较大;在较优解的基础上继续增加迭代次数所获得的网面展开性能提升是由遗传算法对参数的进一步优化实现的,提升幅度较小。最大回弹率由网面质量均匀分布状态下的67.5%降低至网面质量分布优化后的28%;回弹振荡期由网面质量均匀分布状态下的17 s缩短至网面质量分布优化后的7.2 s。本文方法求得的非劣解对应的网面各层质量分布基本重合,且越往网面边缘质量差异越小,如图13所示。
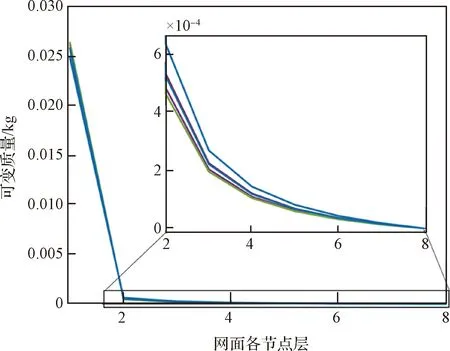
图13 本文方法求得的网面各层可变质量分布Fig.13 Mass distributions corresponding to the Pareto set
选择本文方法中重叠度最高的非劣解作为最优解并提取其对应的网面展开状态和展开率曲线,如图14和图15所示。从网面展开状态上看:最优解对应的网面展开状态良好,网面在展开后基本处于平整状态,仅在最大回弹点时网面中心处有略微回弹;而质量分布均匀的脉冲展开式飞网展开状态相对不稳定,网面的平整度较差,尤其是在最大回弹点,网面出现较大凹陷,且网面边角处有较明显的折叠,如图14所示。从网面展开率方面看:优化后脉冲展开式飞网的回弹现象得到了较好的抑制,发射后网面展开率快速上升且波动小,仅在3 s内即可使得网面展开率稳定在80%以上,网面回弹振荡期缩减至7.2 s内;而对于网面质量均匀分布的绳网则需要在10 s后展开率才能稳定在80%。此外,优化后的脉冲展开式飞网具有更好的展开稳定性,脉冲作用后展开率处于小幅波动状态并逐渐向完全展开状态收敛;而网面质量均匀分布的脉冲展开式飞网仍有周期性的大幅度振荡,难以快速稳定,如图15 所示。因此在相同发射工况下,优化后的脉冲展开式飞网具有更好的展开稳定性。
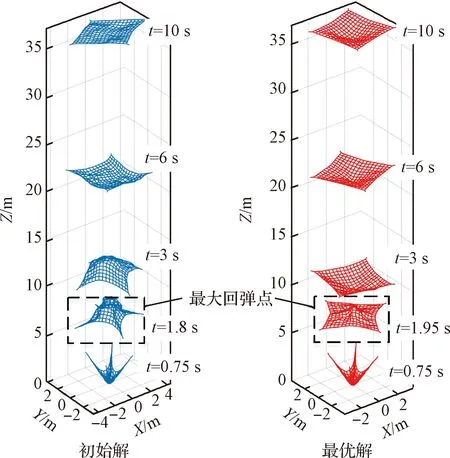
图14 优化前后绳网展开状态对比Fig.14 Comparison of the deployment status of the net before and after optimization
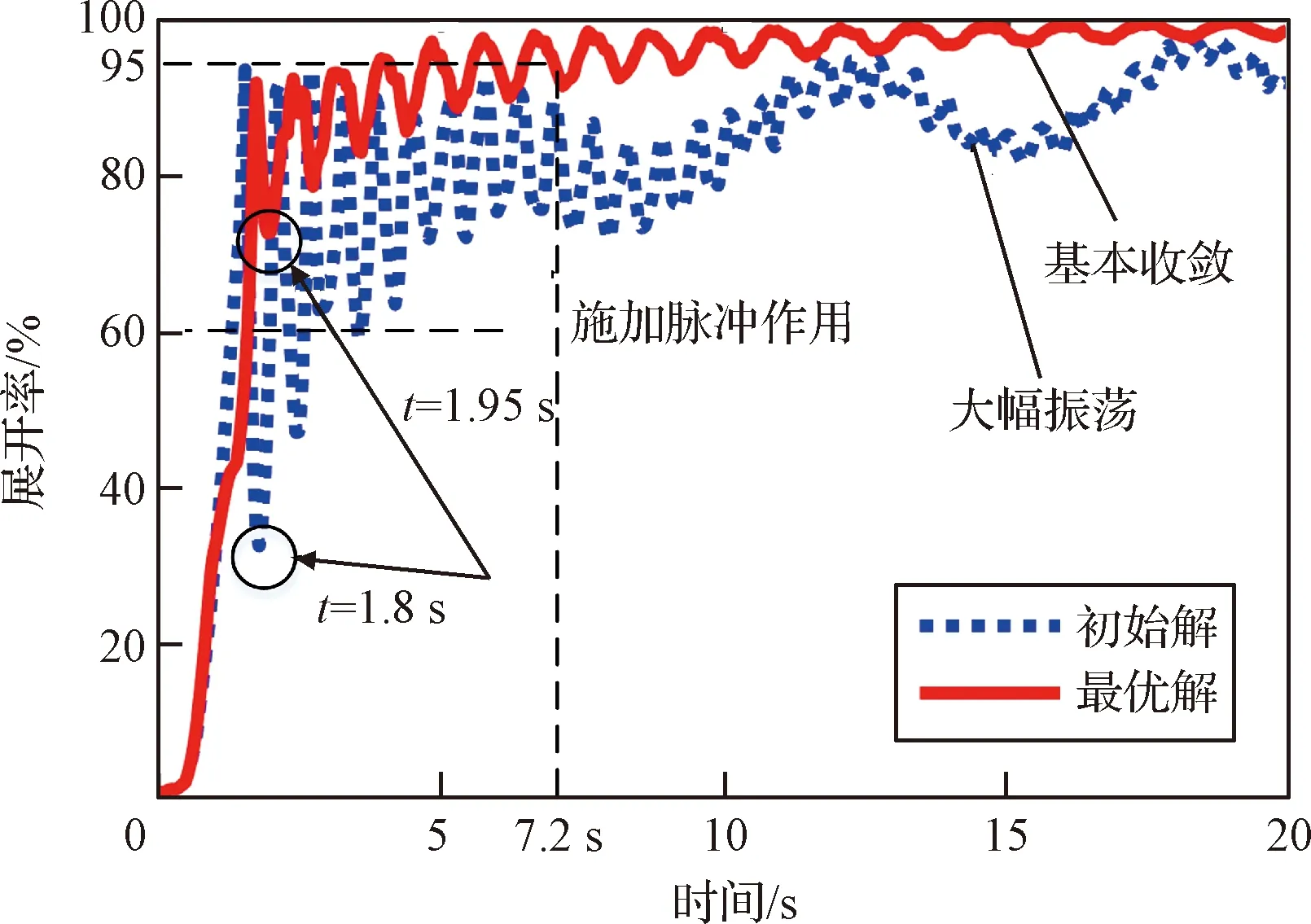
图15 优化前后绳网展开率对比Fig.15 Comparison of the unfolding ratio of the net before and after optimization
同理,采用本文方法对常见的网面节点层数为8~15的脉冲展开式飞网进行网面质量分布优化,得到不同层数绳网所对应的非劣解集合。由相位偏移量的边界条件0<<1,各对应的非劣解可改写为:
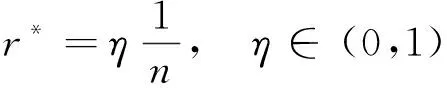
(23)
式中:为小于1的正向比例系数。
由非劣解集合分析得到关于非劣解的正向比例系数∈[0.965,0.985],如图16所示。进一步由线性回归得的线性表达式为:
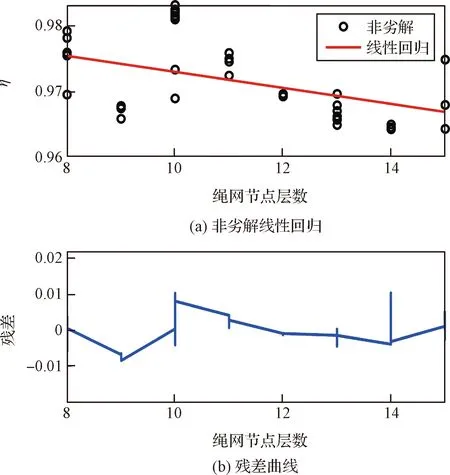
图16 不同层数规格绳网的η的回归分析Fig.16 Regression analysis of η with different nets
=-0001225+09852
(24)
残差分布在±0.01之间。将式(23)、式(24)代入式(19)和(20)得网面质量分布经验式:
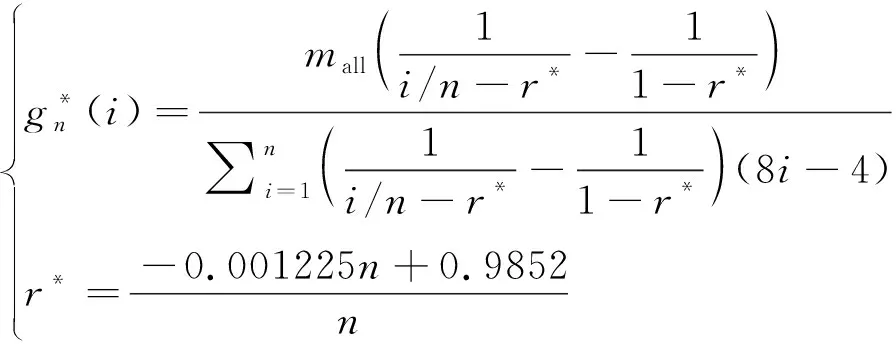
(25)
即对于给定的绳网节点层数为的绳网,可通过代数运算得到优化的网面质量分布。
取={8,9,…,15}分别计算脉冲展开式飞网的网面质量分布经验式,并代入绳网动力学映射与多目标优化、质量均布对应的网面展开情况进行对比。图17给出了单边25格绳网=13的对比结果,网面质量分布经验式具有良好的绳网展开状态,与多目标优化最优解所对应的绳网展开状态基本一致。其余规格绳网的对比结果与之相同,不再赘述。
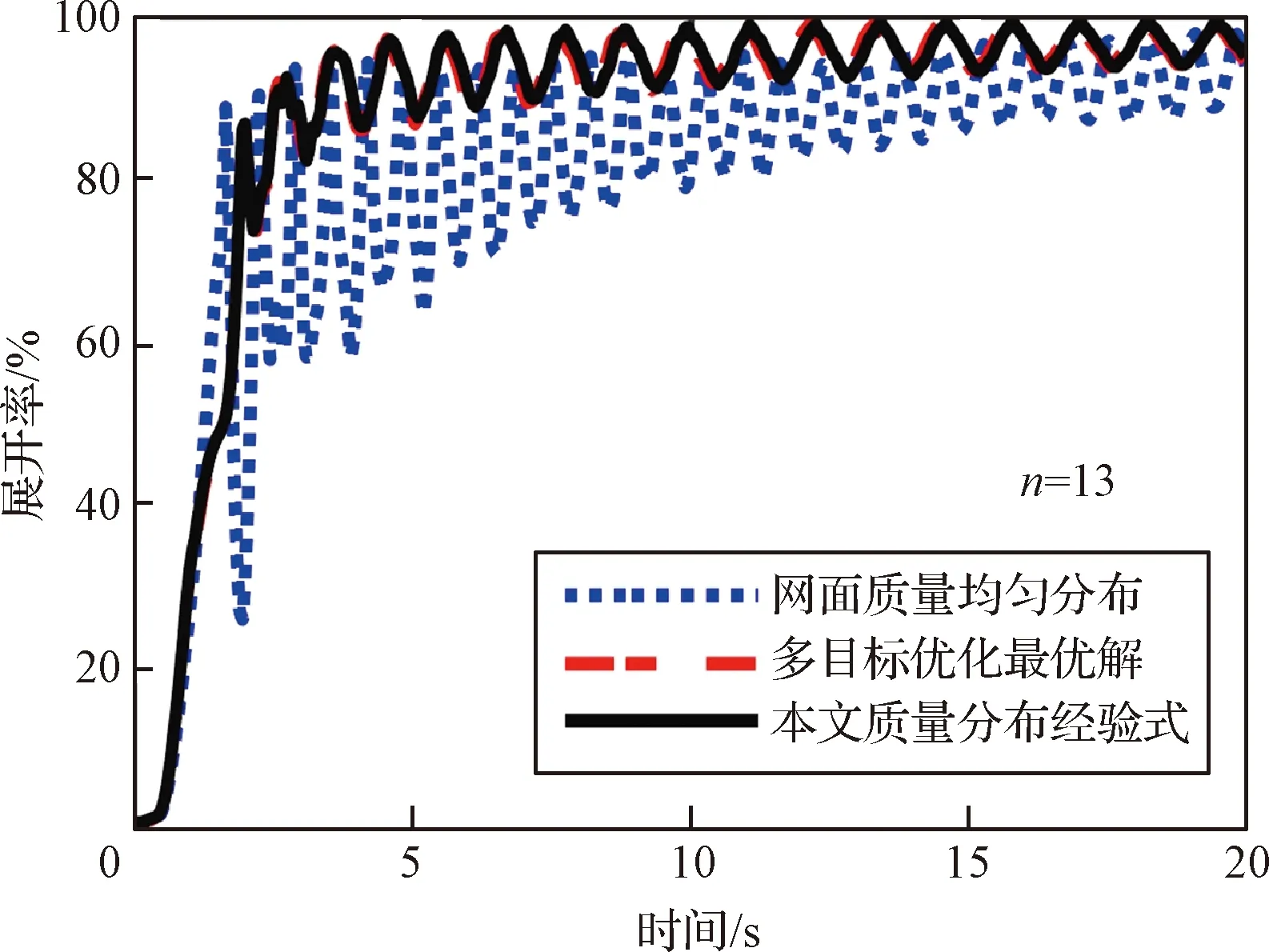
图17 脉冲展开式飞网的展开率对比Fig.17 Comparison of the unfolding ratios of the single-pulse-deployed net
4 结 论
针对脉冲展开式飞网展开后仍存在的较大回弹问题,本文从网面质量分布角度优化提升飞网展开时的稳定性。研究结果表明:1)基于传递矩阵方法和集中质量法推导得到的一维质量分布规律在二维网面中仍然成立,在线性递增、均匀分布、凸形递减、线性递减和凹形递减五个质量分布模型中,凹形递减的网面质量分布所对应的网面展开稳定性最好。2)本文基于反比例函数建立的网面质量分布模型对不同规格绳网均具有较好的适应性,可快速调节相位偏移量,得到不同的网面质量分布状态且极大地降低了网面优化问题中优化变量的个数,提升了绳网优化问题的求解效率。3)最大回弹率由网面质量均匀分布状态下的67.5%降低至网面质量分布优化后的28%;回弹振荡期由网面质量均匀分布状态下的17 s缩短至网面质量分布优化后的7.2 s。4)网面质量分布经验公式所对应的网面展开状态良好,与多目标优化最优解基本一致。
