基于改进遗传算法的战备器材仓库选址优化问题研究

汪琳，何成铭

（陆军装甲兵学院 装备保障与再制造系，北京 100072）

0 引 言

陆军平时器材使用通常由现有器材仓库进行保障，而战时器材保障不同于平时保障的固定性。战时，陆军器材保障是陆军部队作战的重要支撑，对整个战争进程有着重要影响。所以，器材仓库的选址问题就显得尤为重要。临时应急器材储备库的位置选得好，不仅可以降低运输成本，更重要的是在战时可以充分发挥仓库物资的时效性，使器材仓库的战术作用发挥更加明显。

由于野战地点分布随机，与现有器材仓库的距离也并不固定，也就是说，战时仅靠现有的器材仓库无法满足器材保障的需求，必须开设临时器材仓库以实现对战时某一区域的战场器材需求进行及时、准确、不间断的保障，确保战时器材供应保障高效准确、及时稳定。因此，在战时环境下，临时器材仓库选址问题就很有必要进行研究解决。

过去的研究中，关于仓库选址问题的解决方法不多。张帅等人依据微分算法选择库区，引入层次分析法和模糊综合评判建立选址指标体系和建立野战器材仓库选址模型，对仓库位置进行优化配置。罗耀波等人利用改进的遗传算法解决了带退货和软时间窗的地方物流多仓库路径-选址问题。苑德春等人运用四元评价（DFGH）理论分析了影响交通战备器材储备仓库选址的主要因素，并建立了相应模型。严骏等人提出了一种维修器材仓库选址模型的鲁棒优化方法，对定点器材仓库选址的稳定性进行了论证。

在对仓库选址进行评价方面，彭飞等人通过建立评价体系，进一步利用模糊综合评价法研究了仓库选址完成之后的评价问题。邵帅等人还在评价过程中引入了正态云的概念，对于解决仓库选址评估问题中的随机性和模糊性问题发挥了一定的作用。辛昱等人提出基于AHP和模糊物元分析法（FMEA）对物流中心选址方案进行优度评价。

综合上述研究，不难发现过去的研究大多数局限于简单的定量方法，其中模糊综合评价法和AHP的使用尤为频繁，且对于部队战时仓库选址的研究少之又少。本文在对遗传算法进行改进的基础上，对战时器材仓库选址的定量优化进行了有益探索。

1 陆军战时装备器材选址问题

1.1 问题描述

本文通过设定假定条件，在仓库选址问题上运用改进遗传算法在待选战时仓库地址中选取最优点建立临时器材仓库。

器材仓库选址问题可描述为：已知个作战点（，，…，B）的地理位置（，），（，），…，（x，y）和个（，，…，W）可供选择建立临时仓库的待选点位置（，），（，），…，（a，b），运输车从某一仓库待选点出发，将所有作战点遍历一次，并回到原待选点，如何选点能够使得所走路径最短。

为了便于研究，现做出如下假设：

（1）出于战时器材仓库的临时性，单一仓库储存的器材种类可能不能满足所有战场需求，需要至少建立2个或以上的临时器材仓库，本文假设从5个待选地点中选择2个建立仓库即可满足需求；且为保障安全性，5个待选位置均处于战场后方，最终选取的2个器材仓库必须保持一定距离；

（2）凡是某一器材仓库中存在某种类型的器材，则该器材必然能满足所有战场的某次器材需求；

（3）在选址的条件考虑中，器材通过陆路运输，仅考虑路途的远近问题，认为各待选点的自然地理条件均无大差别，不考虑选址点的自然环境；

（4）由于战时环境多变，无法随时保障各个战场与临时器材仓库之间、各器材仓库互相之间信息通信及时、顺畅。因此，假设每次器材运输车出发前往各作战点时，所承载的器材数必然能够满足所有作战点的需求，且器材运输车每次出发必经过所有作战点。

1.2 建立模型

将一个仓库待选点和所有作战点记为顶点集，各顶点间的边集记为，则和组成图=(,)。各顶点间的距离(V,V)已知，设：

其中f表示遍历一次的总路径，(V,V)表示从第个作战点到达第+1个作战点的距离，表示临时仓库。式（1）、式（2）表示对每个点而言，有且仅有一条边进和一条边出；式（3）则保证了没有任何子回路解的产生。

2 利用改进遗传算法求解战时仓库选址问题

2.1 遗传算法

遗传算法的基本思想是根据问题的目标函数构造一个适值函数，对一个由多个解（每个解对应一个染色体）构成的种群进行评估、选择、遗传运算，经多代繁殖，获得适应值最好的个体作为问题的最优解。其通常包含“产生一个初始种群”“根据问题的目标函数构造适值函数”“根据适应值的好坏不断选择和繁殖”以及“若干代后得到适应值最好的个体为最优解”这四个大步骤。

2.2 求解思路和流程

本文中求解器材仓库选址最优方案的总体思路是，在计算过程中，针对每一个待选址点，将其等同于各个作战点，相当于从原来的个点转为从+1个点中去寻找最优路线，从而将问题简化为多个TSP问题。利用遗传算法求解出最优路径，以此作为从该待选址出发，运输车走遍所有作战点，并返回原待选址点的最短路径；将每个待选址点都求出最短路径后，对比选出最优者和次优者作为最终器材仓库的选址位置。图1为算法流程图。

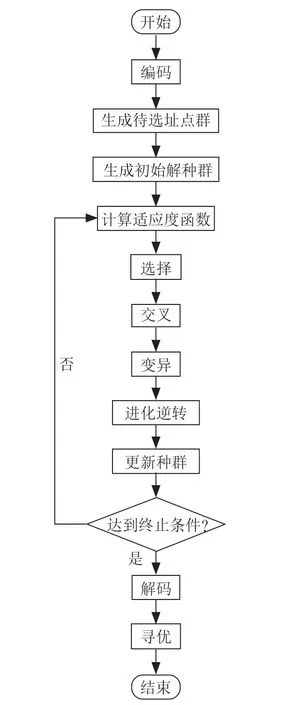
图1 算法流程图

算法基本步骤如下：

（1）随机生成个仓库待选址点；

（2）生成初始解种群：利用initPop()函数生成随机初始种群；

（3）利用适应度函数fitness()计算种群中每个染色体的适应度值，并按适应度值进行排序，计算每个染色体的累计概率；

（4）根据累计概率选择染色体进入新种群；

（5/6）分别按照交叉、变异概率，在新种群中随机选择两个解，进行相应操作；并决定是否将交叉、变异产生的新染色体替换入新种群；

（7）在新群体中选择适应度值最低的解进行进化逆转，并决定是否将逆转产生的新染色体替换入新种群；

（8）检验是否达到终止条件，若未达到，则转步骤3；否则，得出最优解，并从不同待选址点所对应的数个最优解中选出最优和次优所对应的待选址点作为最终的选址点。

2.3 算法详细设计

本文编码方式为顺序编码，即用1到的自然数来编码，其中“0”表示临时器材仓库的位置；1到则表示可能发生战争的作战地点。图2表示了仓库待选点与作战点总数的染色体编码的一种情况示例。

图2 染色体编码示意图

2.3.2 种群初始化

在完成染色体编码之后，必须产生一个初始种群作为起始解。本文选择从含有120个随机个体的群体中寻找最优解进入初始种群，组成含80个染色体的初始解空间。

2.3.3 适应度函数

将适应度函数设置为自“仓库”出发，逐一、无重复经过所有“作战点”，再回到“仓库”的总距离的倒数，即：

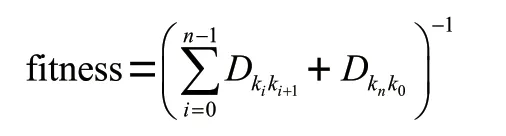
其中D表示从“作战点”k到k的距离，表示“仓库点”。优化的目标就是选择适应度函数值尽可能大的染色体，适应值越大的染色体越优质，反之越劣质。给出了染色体适应值计算的伪代码为：

2.3.4 选择策略

其次，一个场景内，需要各式各样，年代和状况各有不同的建筑，这对于保证区域的地价水平有重要作用。区域内需要有大型企业对产业起到引领作用，因此需要高端商业区域；同时区域也需要考虑小型企业、个人工作室的需求，因此需要相对老旧的房屋场所。同样多样化的房屋可以保证地租水平的稳定，减少居民必要支出，释放消费潜力。在许多对文化创意产业的研究中都发现，地租水平是影响文化创意产业发展的重要因素，差异化的地租，对建立多样化人群的社交网络有重要影响。

对于染色体，设其适应值为F，种群规模为NP，则该染色体的选择概率P可表示为

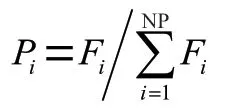
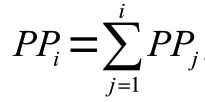
2.3.5 改进遗传算子

对于交叉算子，创新性的提出了同基因交换方式进行交叉。对于两个选定的染色体和，随机选取两个切点和（＞0，＜），逐个比较两切点之间的子串，进行同基因交换。以为例，若其子串第一个位置的基因在的子串中能找到相同基因且处于r（r＜）位置，则改变中该基因的位置为r，并将原先处于r位置的基因调整至子串的第一个位置；若无法找到相同基因，则不改变该基因的位置。同样的，将与未进行交叉操作前的进行同基因交换。若产生的新染色体优于父辈，则将其替换入新种群。图3为染色体交叉示例，经过同基因交换后的染色体不会产生不合法编码。

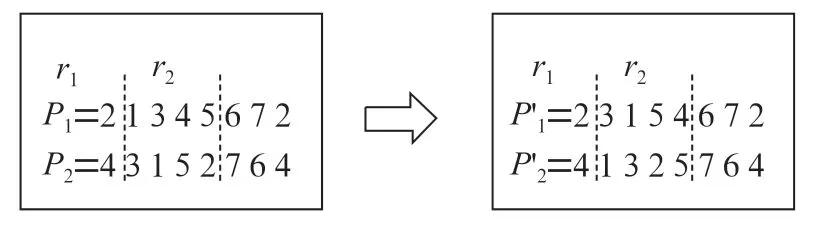
图3 同基因交换示意图

下文给出了改进遗传算法交叉策略与变异策略的伪代码：

%对染色体B进行交叉，操作同上。

变异策略采取随机选取某一染色体的两个位置和，将两位置上的值进行互换：

2.3.6 进化逆转操作

为改善遗传算法的局部搜索能力，在选择、交叉、变异之后引进连续多次的进化逆转操作。

在串中随机选择两点（两点之间称为逆转区域），再将逆转区域内的子串按反序插入原位置中。如图4所示，若新生成的染色体适应度优于原染色体，则进行逆转操作（即进化），否则，不进行逆转。

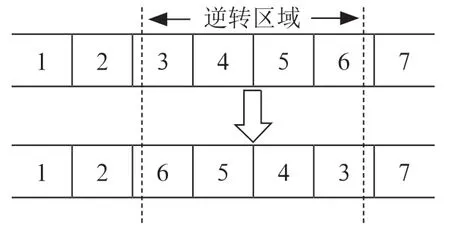
图4 进化逆转示意图（r1=2，r2=6）

进化逆转操作的伪代码为：

2.3.7 停止准则

当寻优迭代次数达到最大遗传代数MAXGEN时，寻优结束。

当整个算法循环次数达到总的待选仓库点数时，算法结束并输出最优和次优仓库位置。

3 实例分析

某战区东南沿海多点同时发生敌方入侵事件，多地局部小规模战争一触即发。临时器材仓库选址建设问题迫在眉睫。

目前，已初步统计出战斗极有可能发生的14处位置坐标，如表1所示。根据前期侦查，发现后方有5处位置可供建设临时器材仓库，如表2所示。目前需要以最快的速度确定2个仓库待建点，以进行临时器材仓库的搭建。

表1 可能的作战地点位置坐标

表2 临时仓库待选点位置坐标

染色体编码为从0-14-0的顺序编码（0表示仓库点），表示器材保障路径为从仓库点出发，遍历所有作战点后返回仓库。

3.1 参数设置

由于在不同种群大小、寻优代数以及交叉变异概率下，改进遗传算法的计算速率有所不同，甚至在待选仓库点较多的情况下，不合适的计算参数为得到最优解可能累积产生极大计算负担。因此，本文为改进遗传算法设置可能的参数取值如表3所示，以便从中选出可能的最优参数选择。

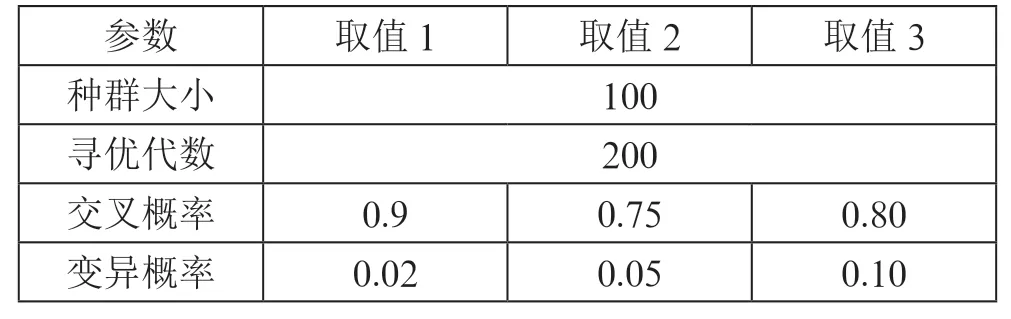
表3 算法参数取值

3.2 算法可行性分析

在表3给出的具体算法参数下，可利用改进遗传算法得到器材仓库选址的最优点和次优点，结果如表4所示。结果显示，采取基于同基因交叉的改进遗传算法时，在合适的参数取值下收敛速度能够明显优于传统遗传算法。并且，当参数取值为第2组时，结果最优。

表4 仓库选址结果

4 结 论

战时器材仓库选址问题面临作战任务的重要性和器材供应的紧迫性，在通过以定性为主的方法（如模糊综合评价法）得出几个待选址点后，需要快速进行更准确的选择。本文通过改进遗传算法，对交叉算子提出了同基因交叉的改进思路，给出了战时仓库精确选址的一种解法，为未来战场应急仓库选址提供可行途径，为提升战场器材保障效率提供了参考依据。