偶数重连续覆盖的Walker星座设计方法
2022-10-15龚宇鹏张世杰
龚宇鹏,张世杰
(1. 哈尔滨工业大学航天学院卫星技术研究所,哈尔滨 150080; 2. 鹏城实验室数学与理论部, 深圳 518055)
0 引 言
Walker星座是由轨道高度和倾角相同的圆轨道卫星组成的规则同构星座,星座中各轨道面沿赤道均匀分布,各轨道所含卫星数量相同且沿轨道均匀分布,具有构型稳定性强、覆盖性能分布均匀、可以灵活调整覆盖纬度范围等特点,被广泛应用于Telesat, Starlink, Kuiper等低轨巨型星座系统的设计。然而当前Walker星座构型设计仍主要依赖于参数枚举、经验公式或智能搜索方法,并未形成通用的设计流程和方法。鉴于偶数与奇数重覆盖Walker星座的覆盖特性存在差异,本文将首先解决偶数重覆盖星座的构型设计问题,并在未来补充研究奇数重覆盖星座的设计方法。
如何使用最少的卫星数量满足星座对地连续覆盖需求是构型设计考虑的首要问题。当卫星数量较少时,可以通过枚举构型并分析覆盖性能获得最优的构型结果,但此类方法难以满足未来卫星数量日益增加的设计需求。覆盖带(Street of coverage, SoC)法是一种通过拼接卫星的覆盖区域解析计算同构星座中卫星的球面距离,进而求解星座构型的设计方法。这种方法不需要预设卫星数量,适用于任意数量规模的星座设计,但由于传统覆盖带方法仅考虑带内卫星位于同一轨道的情况,而Walker星座倾角选择灵活,不同纬度存在多个轨道面交点,难以判定拼接关系,因此并未广泛采用覆盖带方法设计。尽管如此,文献[12]中已经证明,覆盖带存在仍是星座连续覆盖的必要条件。通过分析异轨道面卫星组成覆盖带的特征宽度和拼接关系,就能将覆盖带方法应用于Walker星座设计。
由于Walker星座中不同卫星的升交点经度和纬度幅角相位差不随星座运行而发生变化,因此在(,)相平面内计算星地或星间距离关系可以降低距离求解和覆盖判定的难度。Ulybyshev基于(,)相平面(也称为二维图)分别提出了连续和非连续覆盖Walker星座的构型设计方法。孟少飞等在其基础上提出了一种四重覆盖星座的构型设计方法。然而这些方法并未采用合理的覆盖判定准则,因此所得构型的卫星数量将显著高于实际需求。李翠兰等在星座构型设计时进一步考虑了卫星碰撞风险,对不同(,)分布下的星座碰撞概率估计方法进行了研究。文献[17]中针对相平面内覆盖的判定问题进行了分析,指出当任意纬度目标的可视相位范围在相平面内无缝密铺时,就表示星座可以连续覆盖该目标纬度;结合异轨覆盖带相平面映射的特征宽度,就能判定星座在不同纬度处的覆盖重数,从而计算满足覆盖需求所需的卫星数量和星座构型。
本文将基于覆盖带理论提出一种Walker星座的设计方法。参考Walker星座的构型特点,在(,)相平面内分析覆盖带拼接结果与构型参数的关系,重点解决覆盖重数需求为偶数重时的构型设计问题,旨在为低轨星座系统建设提供参考。
1 同轨覆盖带星座设计
1.1 问题描述
在设定轨道高度和倾角后,Walker星座的空间构型可以由卫星总数,轨道面个数以及相位参数三个特征参数表示,其中表征相邻轨道上两卫星相位之差与2π/的倍数关系。记初始时刻基准卫星的升交点经度和纬度幅角分别为(,),则星座中任意卫星的初始相位(,)可以表示为
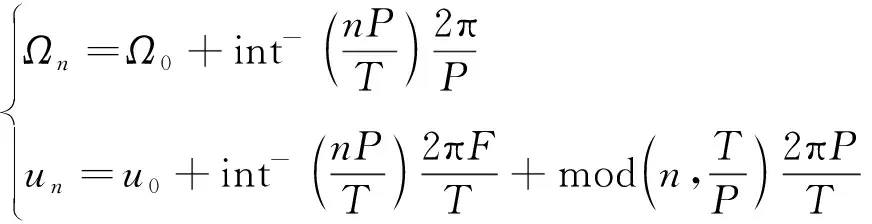
(1)
式中:int(·)为向下取整函数;mod(·,·)为求余函数;=0,…,-1。
如何设计Walker星座的构型参数,,和轨道倾角,使得星座能在给定单星覆盖范围下,利用尽可能少的卫星和轨道数量满足期望的覆盖需求,是Walker星座构型设计所要解决的问题。对于偶数重连续覆盖的Walker星座,由于轨道升降交点沿赤道均匀分布且每轨卫星数量完全相同,因此处于轨道上行段(卫星由南向北运行)卫星的分布情况与下行段(卫星由北向南运行)卫星完全相同。当轨道上行段卫星可以满足期望覆盖重数需求的一半时,另一半覆盖需求将自然被处于轨道下行段的卫星满足。而奇数重覆盖星座需要同时考虑上下行卫星覆盖性能的叠加,其设计思路与偶数重覆盖星座存在差异,本文中暂不对其开展研究。在此可以将偶数重覆盖构型设计问题总结为,求解构型参数,,和倾角,使得星座在卫星数量尽可能少的约束下,轨道上行段卫星可以独立满足目标区域一半的连续覆盖重数需求。
传统覆盖带方法主要适用于覆盖带由同轨卫星覆盖区域拼接形成的情况,本节将首先在这一假设下研究偶数重连续覆盖Walker星座的构型设计方法,并在后续章节中将结论进行推广,分析覆盖带由不同轨道卫星组成时的通用构型设计方法。
1.2 覆盖区域和覆盖带
为设计连续覆盖星座,首先需要计算卫星对地覆盖范围。假设地球是半径为的理想球体,并记卫星对地面可视的最小仰角为,则卫星的覆盖范围可以视作以星下点为圆心,半球心角为半径的球面圆形区域,可根据卫星高度和仰角计算得到。

(2)
覆盖带是由卫星的覆盖区域依次相连形成的条带区域。文献[12]中指出,星座连续覆盖的必要条件是存在覆盖带,即任意卫星的覆盖区域都必须与其它卫星的覆盖区域存在交集。根据组成覆盖带卫星运行方向的不同,可以将覆盖带分为上行段和下行段。为保证连续覆盖,相邻覆盖带间不能存在覆盖间隙,因此可以给出如图1所示的覆盖带距离关系。
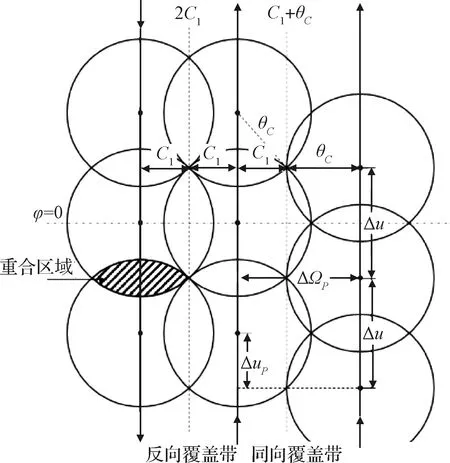
图1 覆盖带的连续覆盖条件Fig.1 Continuous coverage condition for streets of coverage
当覆盖带由相同轨道卫星的覆盖区域组成时,为避免出现覆盖间隙,若同轨相邻卫星覆盖重合区域半宽度为,则同向运行覆盖带间的最大球面距离为+,反向运行的覆盖带最大间距为2。更进一步,当要求重覆盖时,同向覆盖带最大间距为+,反向覆盖带间最大间距为+。重合区域宽度与单轨卫星数量的关系满足
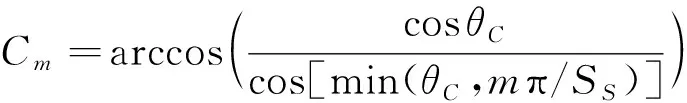
(3)
由于相邻轨道间距随纬度增加而逐渐减小,同向覆盖带在赤道附近距离最远。记星座期望覆盖的纬度范围为[,],满足0≤<≤π2,则当两相邻同向覆盖带在和纬度不存在覆盖间隙时,在任意纬度∈[,]范围内两覆盖带间的区域就一定不存在覆盖间隙。相邻的反向覆盖带出现最大间距的纬度由两轨道升交点经度差所决定,由于本文主要考虑同向覆盖带拼接,在此不进一步研究。
1.3 同轨覆盖带偶数重覆盖星座设计
为使相邻同向覆盖带在纬度不存在覆盖间隙,需要使一侧覆盖带最小宽度与另一侧覆盖带最大宽度同时运行到纬度处。以左侧覆盖带最宽位置与其右侧覆盖带最窄位置拼接为例。当覆盖带最窄和最宽位置运行到目标纬度时,分别对应于左右两侧轨道的纬度幅角和分别为
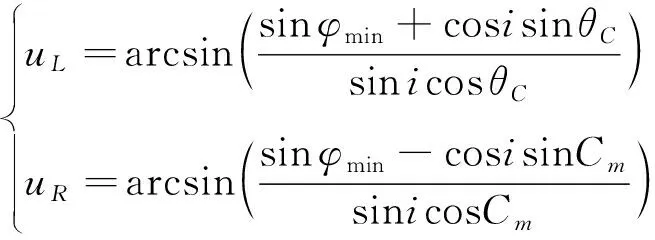
(4)
此时在纬度带上,两侧覆盖带轨迹与轨道星下点的经度差分别为

(5)
由此可以得到满足连续覆盖所需的轨道数量和卫星相位间隔条件
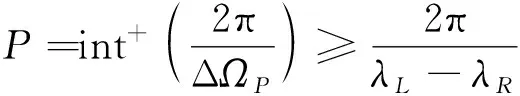
(6)

(7)
式中:Δ=-为相邻轨道的升交点经度差;Δ=-+π为相邻轨道面上卫星的纬度幅角差;int(·)和int(·)分别为向上取整和四舍五入取整函数。
将同轨覆盖带Walker星座的设计步骤总结如下:首先根据期望覆盖的纬度范围[,]和覆盖半径估算初始轨道倾角(例如=-2),随后根据式(3)枚举单轨卫星数量,并计算不同对应的覆盖带宽度。再根据式(6)~(7)计算构型参数,和总卫星数量=。得到星座构型参数后,根据星座在纬度和处的覆盖特性,对轨道倾角进行微调,使得星座在这两个纬度均满足连续覆盖,就基于同轨覆盖带完成了偶数重覆盖Walker星座的构型设计。最后可以通过比较不同对应的总卫星数量和覆盖性能,优选出所需卫星数量较少的构型设计结果。
2 相平面理论基础
尽管覆盖带与轨道重合的设计方法可以满足一般Walker星座的设计需求,但仍存在进一步优化的可能。若令处于不同轨道面的卫星组成覆盖带,可以极大地拓宽构型设计空间,往往能取得更好的设计结果。然而不同轨道面上卫星的星间距离将不断变化,这也会导致覆盖带宽度随卫星运行发生变化,使得相邻覆盖带之间的拼接关系难以计算。
考虑到同构星座中不同卫星轨道参数的差值近似恒定,因此基于轨道参数建立相平面能简化星间距离和覆盖区域几何关系的分析。鉴于Walker星座卫星分布可以由升交点经度和纬度幅角确定,参考文献[14],定义本文中所采用相平面的横轴为,纵轴为,并进一步给出卫星及其覆盖区域空间分布在(,)相平面上的映射关系。
2.1 覆盖区域的相平面映射
为计算覆盖区域的相平面映射结果,首先给出(,)到经纬坐标(,)的转换关系

(8)
式中:arctan(··)定义为值域在[-π,π)上的反正切函数,其取值由分子和分母的符号共同确定。
记卫星的星下点经纬度为(,),任意地面目标经纬度为(,)。由球面几何可知,卫星与目标所夹球心角满足
cos=coscoscos(-)+sinsin
(9)
卫星的覆盖区域即到星下点(,)的球面距离小于卫星覆盖球面半径的点集。考虑到覆盖区域随卫星运行而不断变化,在判定覆盖时更关心星座对纬度的覆盖情况。记可视相位范围(,)为到(,)球面距离小于的相平面坐标集,将式(8)代入式(9)并令=可得
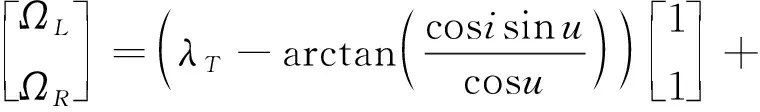

(10)
式中:()=arcsin(sinsin)为星下点纬度。
考虑到三角函数的多值性,式(10)所得结果被分为和两部分,分别对应于可视相位范围左右两侧边界的计算结果。所得结果在(,)相平面内围成了封闭区域,当卫星(,)相位位于所围成区域内时,就可以覆盖目标(,)。图2以=60°,=36°时的可视相位范围为例,展示了不同纬度对应可视相位范围的形状差异。由于同一星下点可能对应于轨道上行和下行段的不同卫星,因此可视相位范围将分为关于(,)=(-π2,π2)中心对称的两部分区域。在分析同向覆盖带拼接时,可以仅考虑||≤π2范围内覆盖区域的拼接关系。
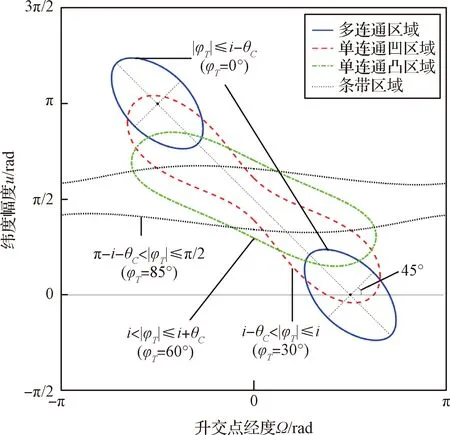
图2 不同φT的可视相位范围形状类型Fig.2 Types of access area mapping with different φT
由前述分析可知,通过在相平面内拼接纬度=和=处的(,)形状,就能判定相邻同向覆盖带在[,]范围内能否密铺。因此可以将卫星实际覆盖区域的拼接关系,转化为相平面内可视相位范围的拼接关系进行求解。
2.2 Walker星座覆盖带构型参数
基于轨道数和单轨卫星数=的构型参数只反映了卫星数量沿轨道面的分布,而与星座覆盖性能无关。本节将改进传统构型参数,提出一种描述星座的覆盖特征的卫星分布表征方式。
对于同构星座中相位为(,)和(,)的两颗卫星和,两星球面距离可以表示为
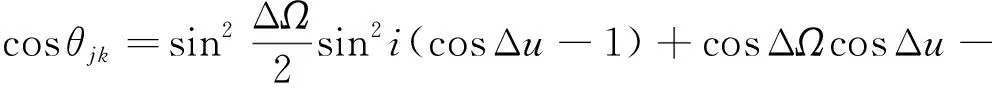
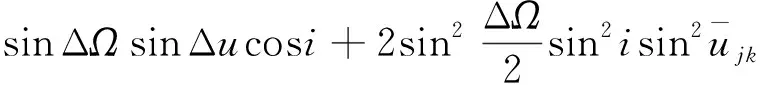
(11)

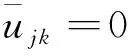

(12)
式(12)可进一步整理为
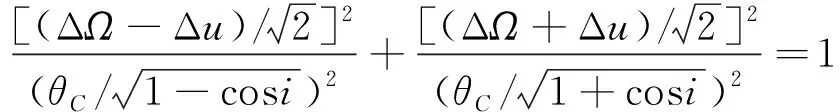
(13)
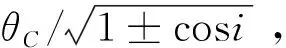
图3以构型(,,)=(36,12,6),倾角=60°,覆盖球心角=28.6°的Walker星座为例,给出了到每颗卫星最大球心距小于的相位邻域。将这些区域依次相连形成覆盖带后,记覆盖带在(-π,π]区间内跨过纵轴和横轴的次数分别为||和,的正负符号取决于覆盖带斜率,若覆盖带与纵轴平行则取=0。定义与的最大质因数为(若=0,则取=)。由此可以将卫星的相位分布表示为:

图3 覆盖带构型特征参数示意图Fig.3 SoC configuration characteristic parameters
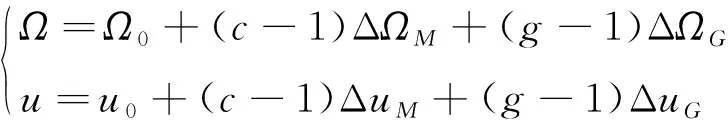
(14)
式中:=1,2,…,,=1,2,…,,分别为覆盖带组数和每组覆盖带上卫星的编号;Δ=2π, Δ=2π,分别为同组覆盖带上相邻卫星的升交点经度和纬度幅角差;Δ, Δ为同组覆盖带相邻轨迹上两颗卫星的相位差。
如图3所示,当=1时,星座中所有卫星分布在唯一一组覆盖带上。这条覆盖带将在穿越(,)相平面横轴次,纵轴次后回到该组起始卫星相位,并留下条横轴间隔为2π的“轨迹”。定义间隔为2π的两条轨迹为同组覆盖带的相邻轨迹。假设覆盖带穿越相平面横轴次后,所得轨迹左侧相邻于起始覆盖带,则满足:
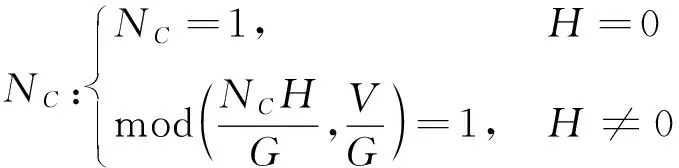
(15)
为描述≥2时卫星的分布情况,需要在基准卫星:(,)同组覆盖带的相邻轨迹上,额外定义一颗参考卫星。记基准卫星右侧相邻轨迹上第一颗纬度幅角不小于的卫星为:(,)。
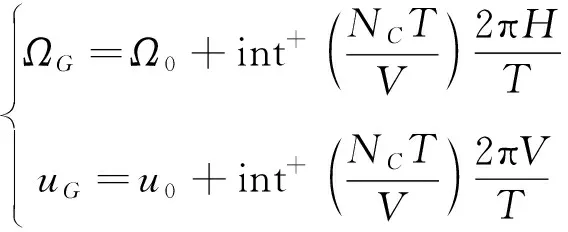
(16)
当≥2时,在每组覆盖带相邻轨迹间还有-1条其他组覆盖带的轨迹。定义其余各组覆盖带起始卫星相位位于与之间时,对应构型参数=0。当>0时,其余-1组轨迹的起始卫星相位将均匀分布在(,)和(+·Δ,+·Δ)之间。因此可得Δ和Δ为
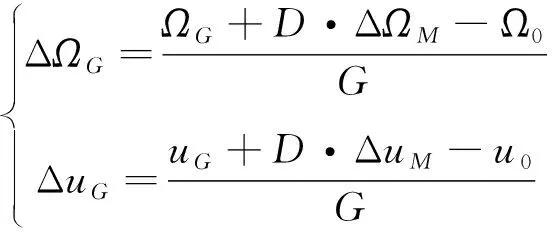
(17)
与传统构型参数(,,)相同,在设定覆盖带构型参数(,,,)后,就可以表征Walker星座中所有卫星的相位分布。例如在图3中覆盖带共穿越横轴6次,穿越纵轴3次,覆盖带斜率为负,且各组覆盖带的起始卫星的相位都分布在相邻同组覆盖带上、两颗纬度幅角相同的卫星和之间。因此该构型同时对应于(,,,)=(36,6,-3,0)的覆盖带构型参数。需要注意由于(Δ,Δ)与(Δ,Δ)的选取并不唯一,同一个Walker星座可能对应于多组不同的覆盖带特征参数。尽管如此,Walker星座仍可以根据期望的覆盖带特性,采用覆盖带构型参数进行设计。
3 异轨覆盖带的相平面映射
与同轨卫星组成覆盖带时设计思路相同,异轨覆盖带的理想拼接情况仍是以覆盖带最宽处与其相邻同向覆盖带最窄处相接,使得两覆盖带的间距最大,从而减少卫星数量。根据文献[17],可以利用特定纬度地面目标的可视相位范围,代替卫星覆盖范围相连形成覆盖带。当所得覆盖带能在相平面内无缝拼接时,就表示星座能实现对该纬度的连续覆盖。(,)相平面上覆盖带的最大宽度,和最小宽度,,以及理想的拼接情况如图4所示。

图4 覆盖带宽度和理想拼接情况示意图Fig.4 SoC width and ideal stitching condition on the phase plane
3.1 异轨覆盖带的最大宽度
记=为(,)相平面内覆盖带的斜率。则当目标纬度为时,覆盖带的最大宽度可以定义为(,)的轨道上行段映射相位(+,+),到与(,)上行段可视相位范围相切且斜率为切线的距离。(+,+)可以根据式(8)求得。
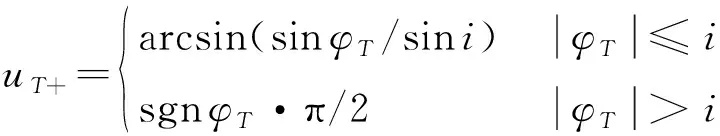
(18)
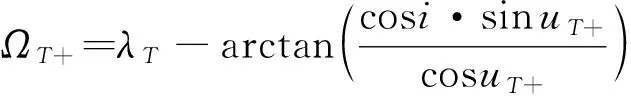
(19)
式中:sgn(·)为符号函数,并假设≤90°。
为避免=0时无法计算,取覆盖带斜率的倒数1=d/u计算覆盖带的最大宽度。式(10)对求导可得
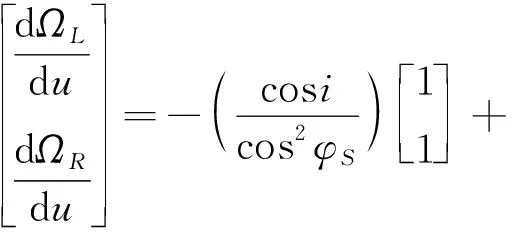
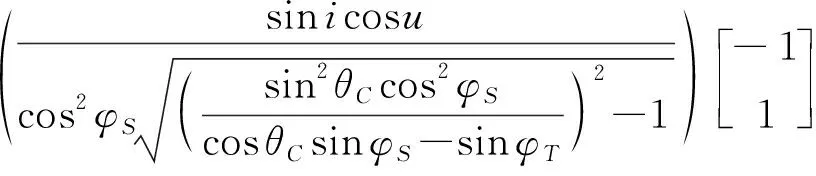
(20)
在图4中,可视相位范围左右两侧分别存在斜率等于的切线。记左侧切点为(,),右侧为(,),和为满足:
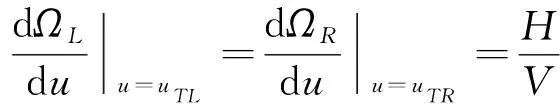
(21)
通过数值方法寻找满足切点斜率为的和,再将所得结果代入式(10)求出切点的升交点经度和,就能计算出对应于纬度的覆盖带左右两侧的最大宽度和。
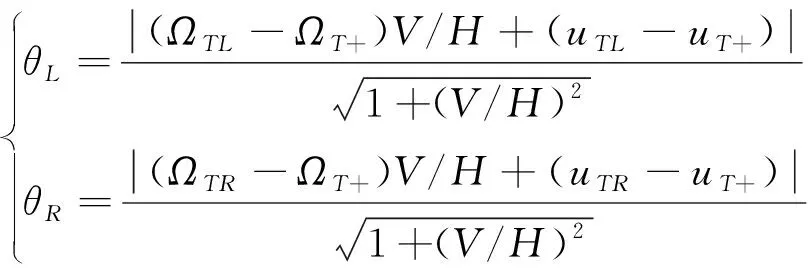
(22)
3.2 异轨覆盖带的最小宽度
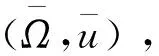
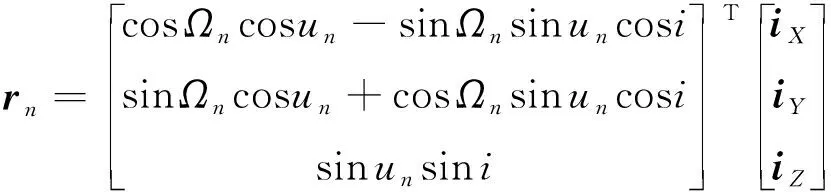
(23)
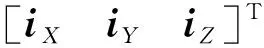
当两星覆盖区域存在交集时,在星下点连线的左右两侧均存在一个交点。记两侧交点空间矢量为和,则有
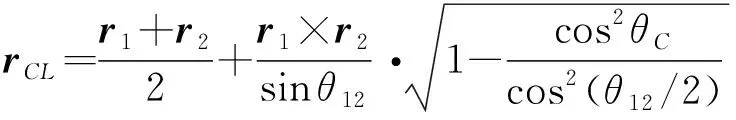
(24)
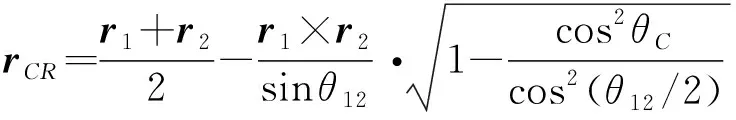
(25)
式中:为到的球面距离,可由式(11)计算。
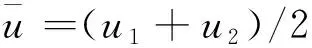
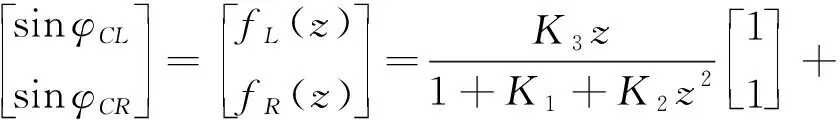

(26)

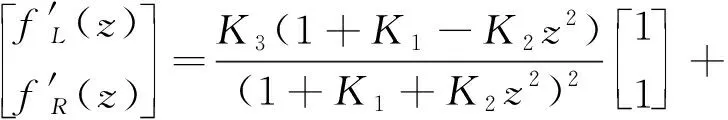
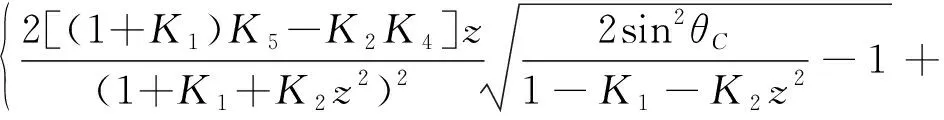
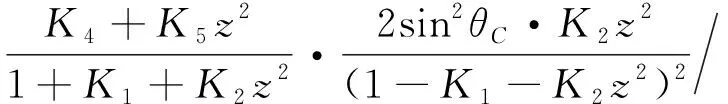

(27)
式中:
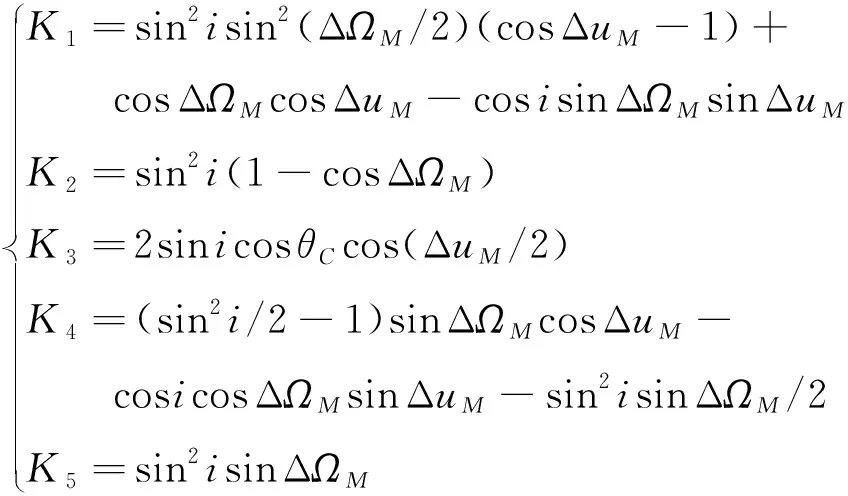


(28)

(29)
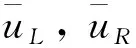


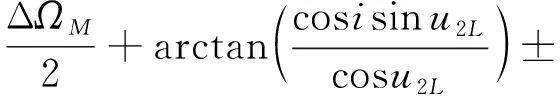
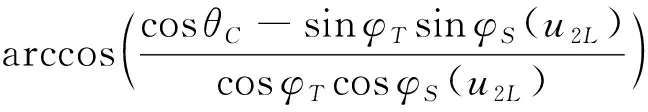
(30)
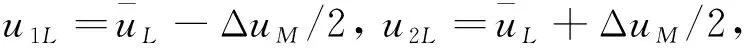
同理可得另一侧交点经度,在得到交点经度和后,就能根据式(18)和式(19)求解交点对应的相平面映射坐标(,)和(,)。
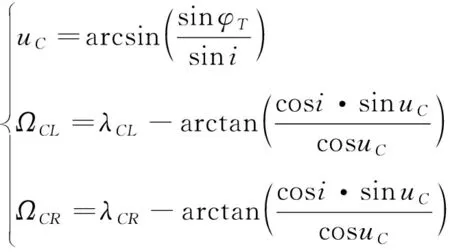
(31)
如图4所示,覆盖带的最小宽度和分别为两星覆盖区域交点(,)和(,)到相平面内两星(,)与(,)所在覆盖带的直线距离,因此有
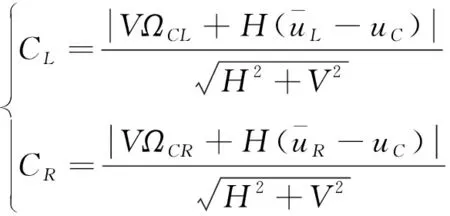
(32)
鉴于覆盖重合区域的交点和宽度求解较为繁琐,在枚举构型时可以将覆盖带间距和最大宽度和相减计算出和的最小值,再利用数值方法计算最小宽度对应的带上相邻卫星相位差和卫星数量,进而提高构型枚举效率。
4 轨道倾角优化
由图2所示可视相位范围类型可知,=π2目标的可视相位范围位于=arcsin(cossin)和=π-arcsin(cossin)之间的条带区域,为使条带区域内的卫星数量恒大于期望覆盖重数,需要求解Walker星座中纬度幅角=的卫星数量,以及星座中任意两星纬度幅角的非零最小差值Δ,由构型参数(,,)计算可得
=gcd(,)
(33)
Δ=·2π
(34)
式中:gcd(·,·)表示和的最大公约数,则使可视相位范围条带内卫星数量大于的倾角满足
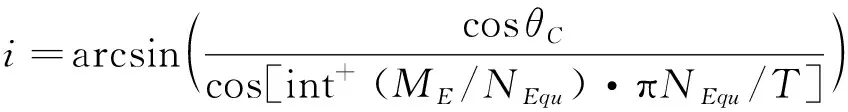
(35)
当<π2时需要保证纬度带上不同经度位置均达到期望的覆盖重数,因此轨道倾角很难解析求解。文献[13]和[15]中均基于二分法给出了倾角的优化步骤,但其覆盖判据过于严苛,因此本文将根据覆盖带的拼接关系优化倾角的求解。
文献[18]中给出了星座连续覆盖的充分必要条件,若任意两星覆盖区域的交点落在时,该交点均至少被其它颗卫星所覆盖,则星座连续重覆盖纬度。由此判据可知,的可视相位范围必须在特定情况下包含+2颗卫星,否则无法实现在纬度的重连续覆盖。
考虑到<π2时可视相位范围是图2中的中心对称单连通凸区域,而Walker星座也存在卫星(,)相位分布关于相平面内某点中心对称的情况。当两者对称中心重合时,的可视相位范围内必须包含+2颗卫星才能保证重覆盖。不失一般性,选取(,)=(0,π2)作为可视相位范围的对称中心,对应于经度=π2的地面目标。由Walker星座构型规则性可知,将(,)设置为以下4种情况时,卫星相位分布将关于(0,π2)中心对称:
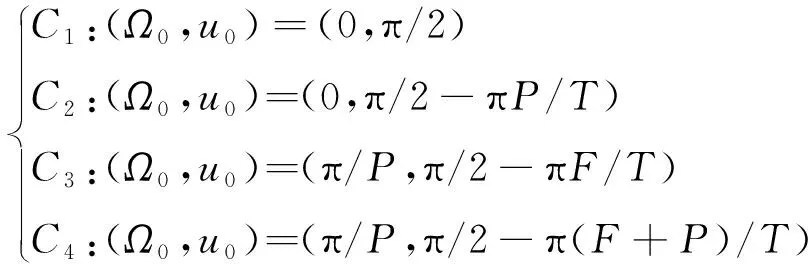
(36)
以上4种情况分别对应于卫星相位、同轨相邻卫星中点相位以及两类相邻轨道卫星中点相位与(,)重合的情况。由于Walker星座的相平面映射可以视为多个平行四边形网格的密铺,因此以上4种类型包括了所有卫星相位关于可视相位范围中心中心对称的情况。通过判定此情况下到对称中心距离最远的两颗卫星覆盖区域交点处的重合重数,就能判定出星座在纬度是否满足重覆盖。由此可以给出图5所示基于二分搜索的Walker星座轨道倾角优化步骤。
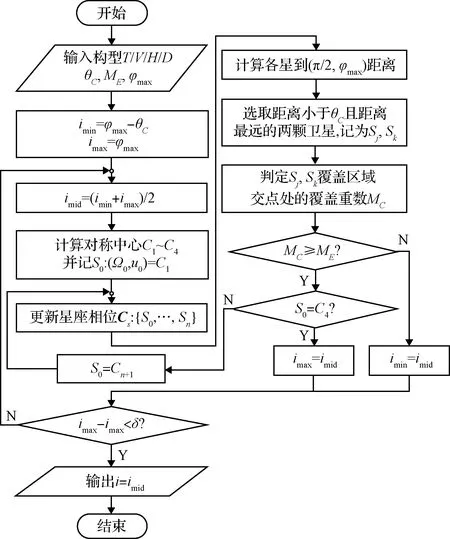
图5 φmax<π/2时的轨道倾角优化步骤Fig.5 Inclination optimization process when φmax<π/2
5 偶数重覆盖Walker星座设计步骤
对于偶数重覆盖Walker星座,只需保证同向相邻覆盖带拼接后达到期望覆盖重数的一半,即可满足设计要求。由于最差覆盖情况仅在期望覆盖的最低纬度和最高纬度处出现。首先根据处的可视相位范围计算同向覆盖带的拼接情况,再根据星座对处的覆盖调整轨道倾角,就能获得理想的星座构型。如图6所示,将基于覆盖带法的偶数重连续覆盖Walker星座的设计步骤总结如下。
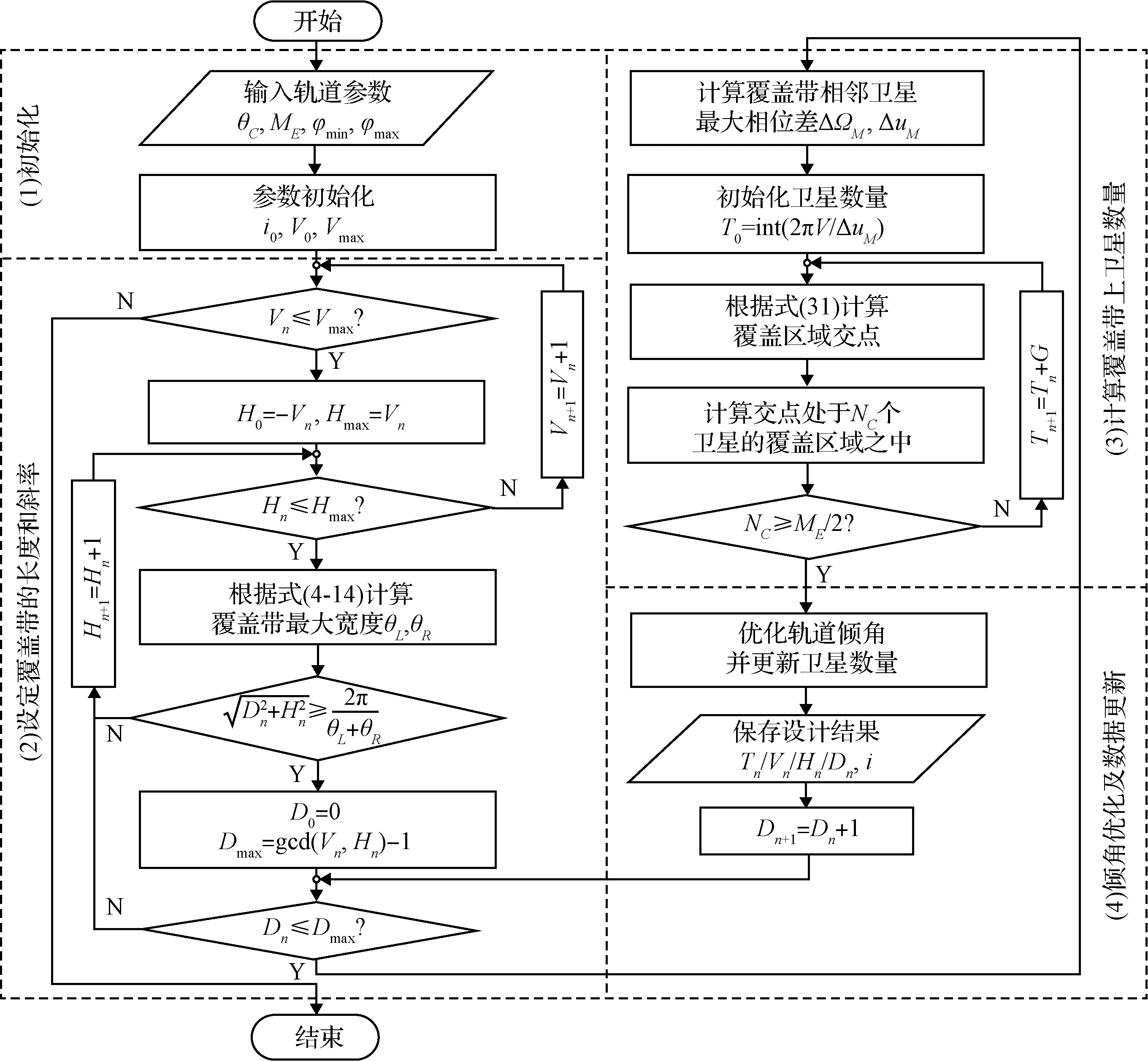
图6 偶数重覆盖Walker星座设计步骤Fig.6 Procedure of even-fold coverage Walker constellation design
1)参数初始化
临床生化检验属于医院重要工作内容,生化检测结果的准确性对诊断和治疗疾病产生直接影响[1]。血液样本溶血是指血液样本在临床检验过程中由各种因素影响导致红细胞被破坏,而细胞内物质进入血清,使得血清呈现出红色,进而影响生化检验结果准确性的医学现象。在当下临床检验实践过程中,若因血液标本溶血导致结果不准确而引发的医疗纠纷,医院往往处于被动地位,并可能需要承担全部责任,所以临床上如何避免或预防血液溶血对生化检测结果带来的影响依然是临床检验科室面对的焦点问题[1]。此外临床对纠正溶血所产生影响的措施缺少关注。本研究对溶血对生化检验准确性影响进行分析并总结相关应对措施,现将相关内容总结如下:
首先根据单星覆盖范围和覆盖需求,粗略估计轨道倾角,并确定覆盖带与相平面横轴相交次数,即特征参数的取值范围。由式(13)可知,相平面上到卫星的最大距离为的相位范围可以等效为一个椭圆。因此同向覆盖带间的最宽距离不能大于椭圆的长轴,否则相邻覆盖带间的覆盖区域不可能存在交集。同时覆盖带间距也不宜太窄,因此令覆盖带的最小间距大于椭圆的半短轴,即令覆盖带只与相邻同向覆盖带的覆盖区域存在交集。在输入单星覆盖半径,期望覆盖重数以及期望覆盖的纬度范围[,]后,可以将初始轨道倾角和构型参数∈[,]的范围选定如下
=-(2+1)
(37)

(38)
2)设定覆盖带长度和斜率(设定,,)
由于同向轨道间距随纬度升高而逐渐减小,因此可以根据纬度目标的可视相位范围映射形状,确定覆盖带构型参数和的取值范围。依次枚举构型参数和,并根据式(22)计算出对应不同斜率的覆盖带左右两侧最大宽度和。当相邻同向覆盖带间距小于+时,可以通过增加覆盖带上卫星使相邻覆盖带实现密接; 反之则表明无论如何增加覆盖带上的卫星,相邻覆盖带间均会存在覆盖间隙。相邻同向覆盖带间距需满足:
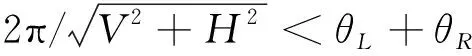
(39)
3)计算覆盖带上的卫星数量(计算)
在确定构型特征参数和后,相平面上的覆盖带就被唯一确定,随后需要计算使处达到重覆盖的卫星数量。在图4中,当的可视相位范围在一侧与一条覆盖带相切时,另一侧区域与相邻覆盖带两个交点之间的相位差即为覆盖带上相邻卫星的最大相位间隔。随后根据这一相位差和覆盖带总长度计算出所需的最少卫星数量。最后,继续增加卫星数量,直至覆盖带最窄位置被其相邻覆盖带上至少2颗卫星覆盖。
4)倾角优化及数据更新(优化)
以上步骤保证了星座对于[,]纬度区间的重连续覆盖。由于最高星下点纬度等于轨道倾角,因此对于纬度高于轨道倾角的区域,星座覆盖能力将随纬度升高而迅速下降。根据星座对于纬度的覆盖性能优化轨道倾角,并在优化后重新执行步骤(3)更新卫星数量,保证纬度处的覆盖性能不受影响。保存每组构型及对应的卫星数量和轨道倾角,直至所有可行构型参数计算完成。
6 仿真校验
为验证覆盖带方法的可行性,本节将首先以文献[4-5]中,由构型枚举法得到的最优(相同卫星数量下单星覆盖半径最小)Walker星座的单星覆盖半径作为覆盖带法的设计输入,设计并对比给定覆盖范围下的偶数重连续覆盖Walker星座的构型结果。随后结合低轨巨型通信星座系统实例,进一步验证所提出方法在星座设计领域的应用价值。
6.1 偶数重覆盖星座设计结果
图7以全球二重覆盖Walker星座构型设计为例,对比了地面仰角=5°约束下三种设计方法的耗时。同轨覆盖带星座由于约束了构型而不需要进行枚举,因此基本能在10s内获得构型设计结果。本文方法需要枚举覆盖带构型参数,因此仿真耗时略有增加,但仍能在2~4 s内完成构型计算。
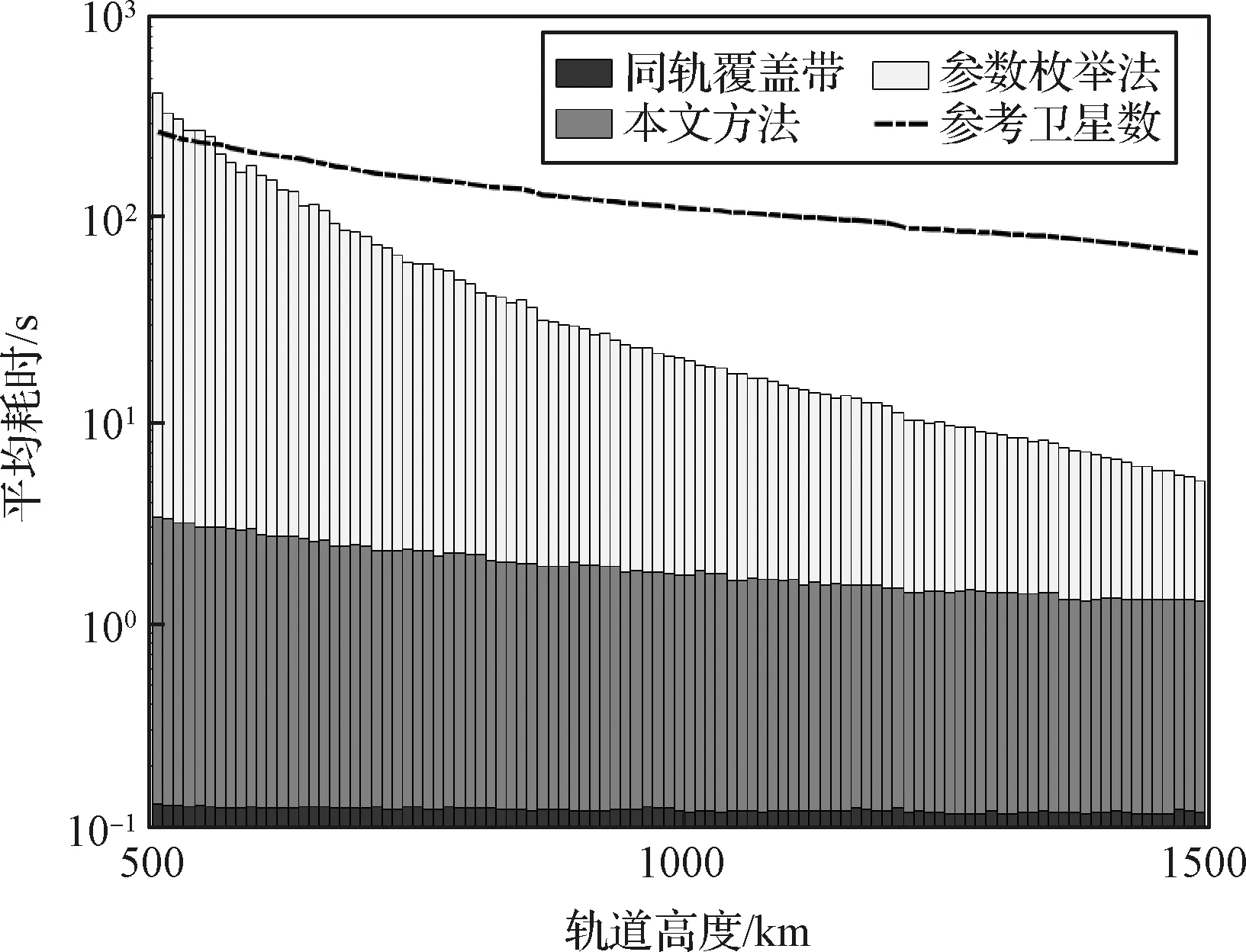
图7 各构型设计方法耗时对比Fig.7 Time consuming of the three configuration design methods
参数枚举法需要枚举不同卫星数量下所有可能的轨道和卫星相位分布组合,因此方法耗时将随卫星数量增加而显著增加。在卫星数量规模约为200颗时,本文方法耗时仅为构型枚举法的1%,且计算时间减少比例会随单星覆盖范围的减小而进一步提高,因此更适用于巨型星座的构型设计问题。
记枚举法给定卫星数量为,相同覆盖范围约束下采用本文方法和同轨覆盖带方法设计所得卫星数量结果分别为和,并分别定义和为枚举法和同轨覆盖带法,与本文方法所得卫星数量误差的百分比。
=100×(-1)
(40)
=100×(-1)
(41)
图8和图9分别给出了不同单星覆盖范围下,Walker星座实现全球二重和四重连续覆盖所需的最少卫星数量。由图可知本文方法所计算得到的星座构型,与枚举所得最优构型结果的卫星数量误差一般不超过10%。而对于传统同轨道覆盖带星座,由于其卫星总数必须能被分解为轨道数及每轨卫星数量的乘积且需要合理分配轨道和卫星数量,因此达成覆盖所需的卫星数量将增加约10%到20%。
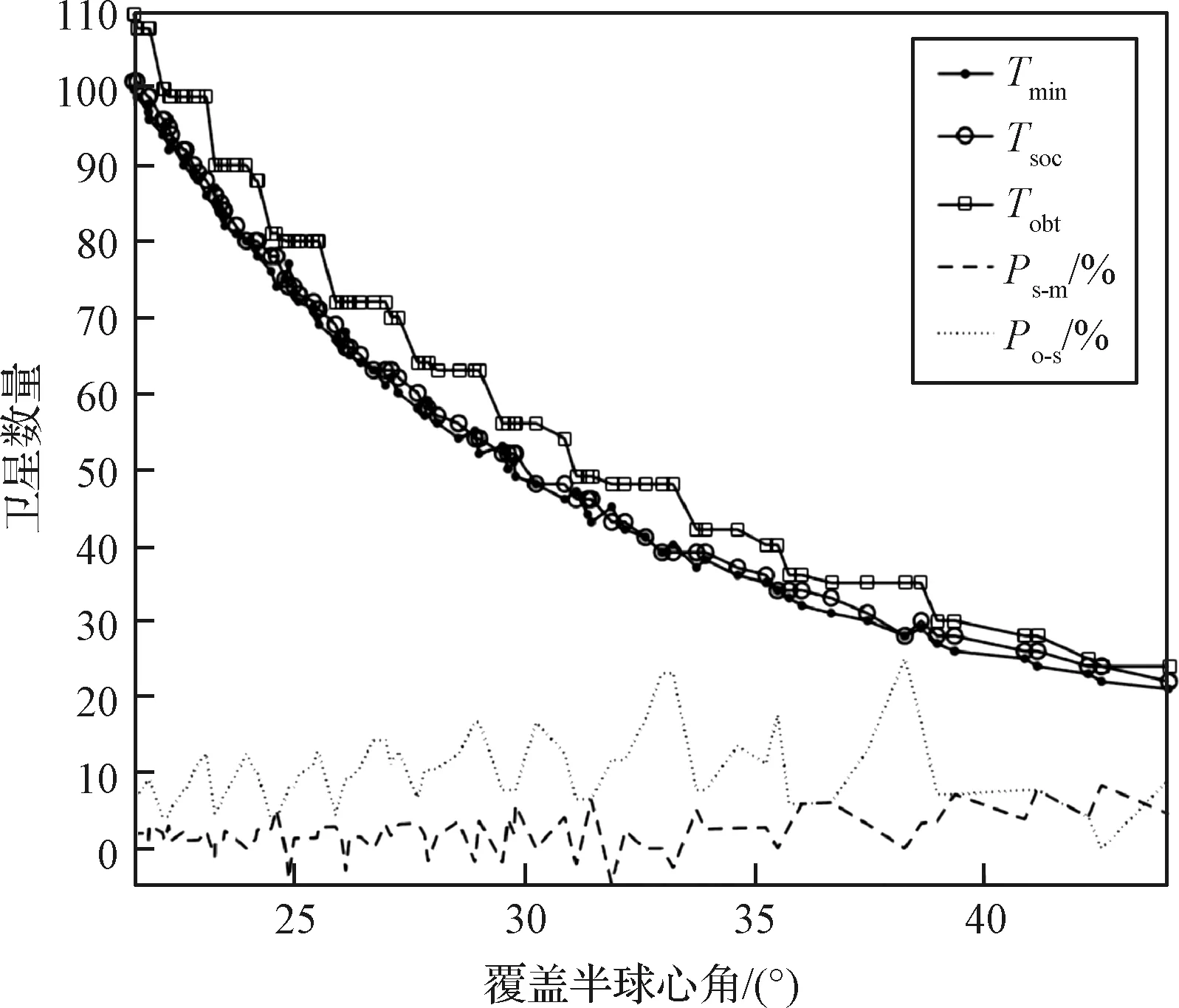
图8 全球二重覆盖星座卫星数量Fig.8 Number of satellites for 2-fold global coverage

图9 全球四重覆盖星座卫星数量Fig.9 Number of satellites for 4-fold global coverage
在少部分情况下,覆盖带方法所得结果将优于枚举出的给定卫星数量下最优构型。这是由于当卫星总数为质数时,只能采用每条轨道一颗卫星的构型。这种构型限制使得卫星数量增加反而可能造成星座覆盖能力的下降。而采用覆盖带法设计不需要预设卫星数量,因此将直接取得卫星数量更少且卫星覆盖范围更小的构型结果。
图10和图11分别给出了中低纬度及中纬度条带的构型设计结果。当覆盖区域不包括赤道时,上下行覆盖带的覆盖性能将相互耦合,因此两者独立满足一半覆盖重数需求的假设相对保守。但本文方法与最少卫星数量结果误差仍不会超过10%。
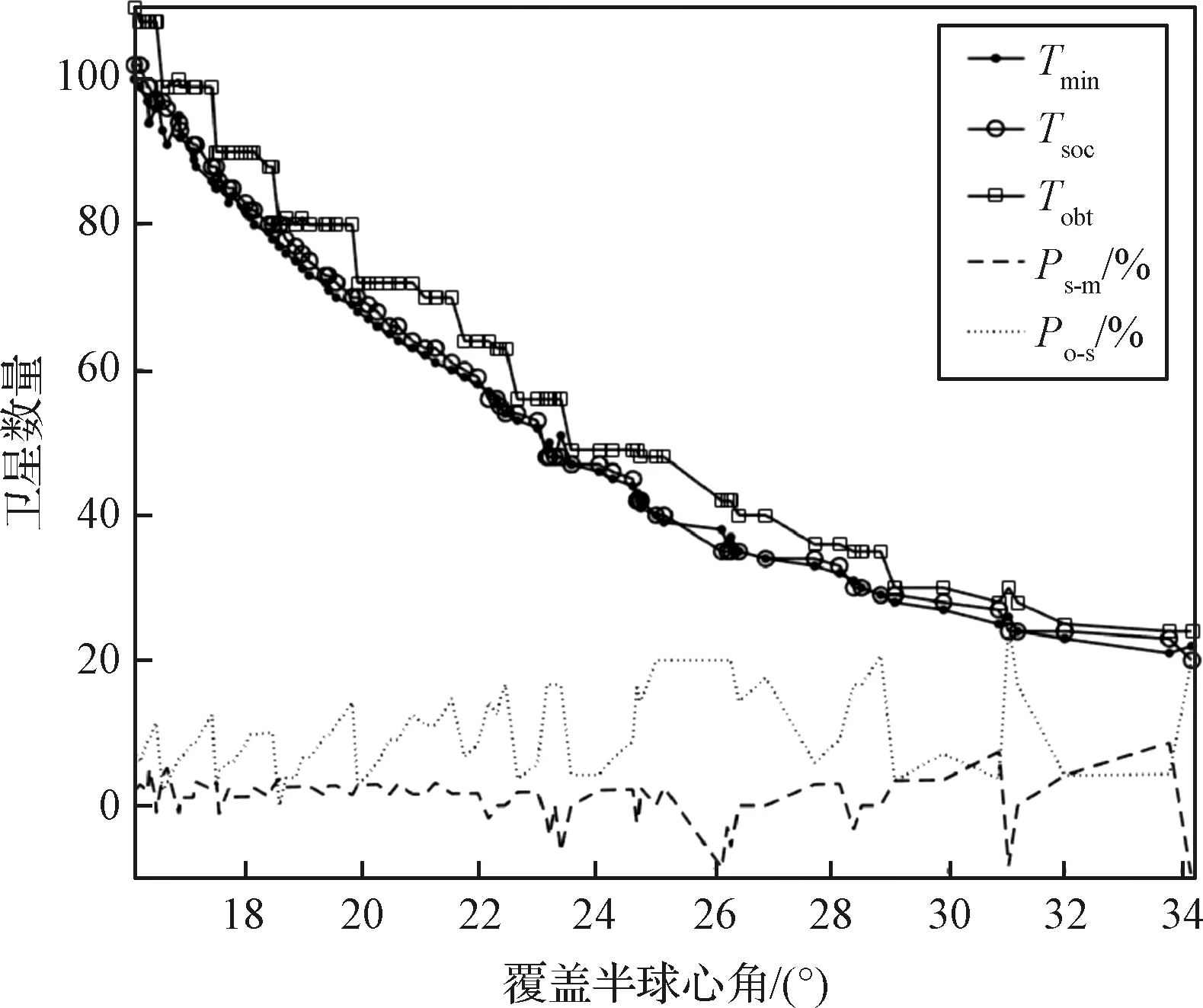
图10 南北纬65°二重覆盖星座构型结果Fig.10 Number of satellites for 2-fold 65° S~65° N coverage
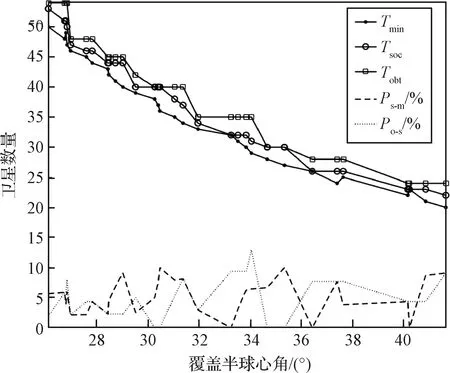
图11 20°N~65°N二重覆盖星座构型结果Fig.11 Number of satellites for 2-fold 20° N~65° N coverage
6.2 巨型星座系统构型设计实例
本节以亚马逊公司提出的Kuiper互联网星座系统为例,进一步验证所提出方法在星座构型设计领域的应用价值。Kuiper系统规划最低工作仰角设置为35°,由3层高度及倾角不同的Walker星座组成,旨在为全球95%人口所在的南北纬56°之间区域提供低时延的入网服务。经过分析,可以确定该系统采用的是以轨道作为覆盖带的双重覆盖星座构型,其构型参数及预期覆盖范围如表1所示。

表1 Kuiper星座系统构型及轨道参数Table 1 Configuration and orbit parameters of the Kuiper constellation
将各批次Kuiper星座系统的轨道和构型参数作为星座构型设计的输入,计算单星覆盖范围与各批次条件相同时,达成覆盖需求所需的卫星数量和星座构型。表2给出了基于所提出覆盖带方法的部分星座构型设计结果。

表2 参考Kuiper星座构型设计结果示例Table 2 Configuration results referring to the Kuiper constellation
图12对比了相同单星覆盖范围约束下,所得构型与现有Kuiper系统构型的最低覆盖重数在各纬度的分布。相比于现有构型,本文方法可以在最低覆盖重数不变的情况下,将覆盖所需的卫星数量减少约10%。考虑到卫星数最少的构型结果可能需要过多的轨道数量,大大增加星座部署和构型维持难度。通过在覆盖带上增加少量卫星,或是选择次优的构型可行解,均能在覆盖特性基本不变的前提下,减少轨道数量并获得可行的构型设计结果。

图12 Kuiper与优化构型的最小覆盖重数对比Fig.12 Minimum coverage folds of Kuiper and modified constellation configuration
值得一提的是,卫星数量和覆盖性能并非是星座构型设计所需考虑的唯一因素。星座系统往往为了保证性能余量和抗毁能力,而采用卫星数量稍多,但鲁棒性和综合性能更强的构型。在星座构型设计时,可以首先采用本文方法计算满足覆盖需求的最少卫星数量,再沿覆盖带增加卫星,进一步提升星座的构型鲁棒性和降阶运行能力。
7 结 论
本文针对偶数重连续覆盖Walker星座的构型设计问题,基于覆盖带方法改进了传统星座构型的表征方式,分析了异轨覆盖带相平面映射的宽度特征,并提出了轨道倾角优化和构型设计方法。所提出方法适用于任意卫星数量规模和纬度覆盖需求,能有效解决Walker星座的构型设计问题。仿真实例表明,该方法所得构型与传统同轨覆盖带构型相比能减少约10%覆盖所需的卫星数量,且与满足覆盖所需的最少卫星数量相近,并能通过调整覆盖带构型参数进一步优化构型包含的轨道数量。
