带止步、中途退出和负顾客及反馈的MX/M/1/N多重工作休假排队系统
2022-10-14王莉
王 莉
(宿迁学院 文理学院,江苏 宿迁 223800)
随着现实生活的实际需求,休假排队系统的研究已愈发广泛和成熟,并在现实生产生活中得到了广泛的应用.但是,本着高效节能的原则,在休假模型中需要做进一步的优化设计,这就需要对系统进行设定,一般要求在休假期内,服务员仍处于待工作状态,如果有顾客,就会进行服务,但是服务的效率要低于正常工作时的服务效率.比如银行系统,在工作日内的每天中午时段,服务窗口会减少,只安排少部分人员工作,但不会关闭所有窗口,这种工作模式的休假称为工作休假.如果工作休假期间,服务员的服务效率降为零,将变成经典休假模式.
近年来,在休假排队模型的研究中,工作休假排队模型成为国内外学者关注的焦点[1-4].与此同时,在工作休假模型中考虑负顾客的侵入影响的研究[3-5]也逐渐增多,这里所指的负顾客规定为非正常到达的顾客,它是外来一些随机因素对服务台的影响,它可以消除队列中的正常顾客,如果系统中没有顾客,此时外来随机因素带来的影响会自动消失.在工作休假模型中考虑止步和中途退出两个因素的研究[6-8]也不在少数.另外,多重工作休假、带反馈机制的排队模型也都是当前研究的一个热点[9-11].
然而同时将止步、中途退出、负顾客、反馈机制同时考虑在多重工作休假系统中的文献还比较少.基于此,本文在MX/M/1/N多重工作休假模型中同时加入了止步、中途退出、负顾客、反馈及批量到达等六个因素后研究系统稳态下的性能指标,为今后这类模型在实际应用中提供参考和依据.
1 模型描述
本文的新意在于在简单的MX/M/1/N多重工作休假模型中同时考虑了因不耐烦情绪造成的止步和批量到达两个因素的新模型,同时结合负顾客、中途有退出机制和反馈策略进行了讨论.在增加负顾客后,系统出现了正、负顾客两种类型,系统的服务机制是一次只服务一位顾客的单服务台系统,最大服务量为N,如果系统中的正顾客数大于规定的临界值,就不容许再有正顾客进入.
模型的具体规定如下:

相互独立且都服从两点分布.则X为到达的这批顾客的总数量,其概率分布为:
为方便起见,记mn=P(X=n),0≤n≤N.这里mn=P(X=n)≥0.
2)服务台对成批次到达的正顾客的服务顺序是按到达的先后顺序进行服务.服务台对每批次中的顾客施行随机选择的形式服务,且服务顾客的时间服从负指数分布.
3)系统中有工作休假和忙期两种状态。忙期时,系统服务顾客的效率μb是正常的,忙期结束后系统为空时,会进入一个时长为V的工作休假期,且随机时长且服从参数为θ的负指数分布,假期内到达的顾客也接受服务,但服务的效率μV(μV<μb)会比忙期低.如果一个时长的休假期结束后,系统是空的,那么将继续一个完全相同时长的休假;反之,如果一个假期结束时系统不是空的,那么结束假期进入忙期,当系统不再有顾客时,结束.两种状态下系统的服务时间都服从负指数分布.顾客结束服务后可能会直接离开,也可能继续反馈到队尾等待第二次服务,设直接离开的概率为p(0 4)设定负顾客到达率为ε,负顾客的出现会消除排在第一的正顾客,且一抵一消除,否则会自行消失. 5)在排队等待的顾客会因队长而不耐烦,而选择中途退出.设定顾客在系统内停留的时间分布是负指数分布,参数为α,则有顾客在系统忙期时的中途退出率为 r(n)=(n-1)α,2≤n≤N 相应地,顾客在系统工作休假期的中途退出率为 r(n)=nα,1≤n≤N 6)本模型中只设置一个服务台,一次只服务一个顾客,顾客进入系统如无其他顾客,则会马上接受服务,否则需要等待.服务过程与到达过程是相互独立的. 假定服务过程与到达过程且以上各随机变量间均相互独立. 令L(t)表示系统在t时刻的队列长(顾客数),t≥0.令J(t)表示服务员在t时刻的服务状态,有: 则{L(t),J(t),t≥0}为二维马尔科夫过程,其空间状态为 Ω={(n,0):0≤n≤N∪(n,1):1≤n≤N} 系统的稳态概率定义如下: 由马尔科夫过程理论可得系统稳态概率满足的方程组为 (1) (2) (3) (4) (5) [pμb+ε+(N-1)α]P1(N) (6) 其中,方程(1)-(3)代表顾客在系统休假期间到达系统时的状态变化情况,方程(4)-(6)代表系统由休假期进入忙期的情况. 用下列分块矩阵表示系统的状态转移率的矩阵 其中 注A1是N+1阶方阵;B是(N+1)×N阶矩阵;C是N×(N+1)阶矩阵;A2是N阶矩阵;O1为N维零行向量;O2为N-1维零列向量;O3为(N-1)×N阶零矩阵;EN是N阶单位阵. 证明参见文献[12]. 定理1将A1写成如下分块矩阵 证明完毕. 证明 记DN=|A2|,考虑到DN的形式可得出,把DN的其它N-1列都加到第一列上,再将第一列按展开法展开得出DN=-(μb+ε)DN-1,其中DN-1是比DN的低一阶的具有相同结构的行列式. 同理可得: DN-i=-(μb+ε+iα)DN-i-1,1≤i≤N-2 D1=-[pμb+ε+(N-1)α] 证明完毕. 记εn(1≤n≤N)为N维单位列向量,eN+1和eN依次为元素均为1的N+1维、N维列向量,e代表元素均为1的2N+1维列向量. 定理3系统的稳态概率为 P0(0)=δ (7) (8) (9) 证明 定义稳态向量 P0=(P0(0),P0(1),…,P0(N)),P1=(P1(1),…,P1(N)) 记P=(P0,P1),稳态向量满足: (10) 用分块矩阵的形式(10)式可以表示为 (11) P0eN+1+P1eN=1 (12) 将(11)式展开得 (15) 从而得到: (16) 由此得: (17) 由(14)式得 展开并将(16)式代入可得 (18) 将(17)和(18)式代入(12)式可得 (19) 把(19)式代入(17)、(18)式整理可得系统的稳态概率为 证明完毕. 1)服务员处在忙期的概率 (20) 2)服务员工作休假的概率 (21) 3)系统的平均等待队长 (22) 4)系统的平均队长 (23) 5)顾客的平均止步率 (24) 6)平均的中途离去率 7)顾客的消失概率 由于多重工作休假系统在实际应用中复杂多变,将简单的休假模型做了复杂化的处理,添加了批量到达、负顾客、止步和中途退出四个实际中的控制因素,建立了一个多重工作休假排队系统的新模型,通过运用基本的排队理论和方法得出了新模型的一系列重要的性能指标,这为该模型的实际运用提供的理论依据,同时为工作休假进一步深入的研究也提供了参考.2 稳态概率方程组

3 稳态概率的矩阵解法





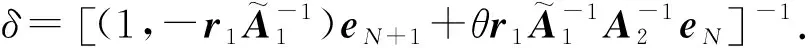




4 系统的性能指标
5 结论
