大气摄动力作用下卫星轨道仿真

薛申芳，谢小军

(广州工商学院，广东 佛山 510850)

0 引言

在讨论大气对卫星轨道的影响时，我们是针对高层大气(高度在90 km以上).大气密度不仅与高度有关，而且与地球形状、昼夜、季节、大气旋转等有关，其规律相当复杂，尽管大气模型不断地得到改进，仍然存在15%～30%的误差[1].测量资料已经证明了大气密度分布所具有的特征[1]：大气密度随高度增加而减小，减小的速度随高度的增加而变缓，等密度面接近于地球形状；太阳辐射显著影响大气密度分布，且卫星轨道越高，这种昼夜、周日、季节变化越大.高层大气在200 km高度上可相差3～4倍，在500 km高度上可相差20～30倍，在1 000 km高度上可相差100倍.这里采用通常使用的大气近似密度的指数分布函数给出大气阻力以及大气旋转作用下卫星轨道模型，采用四阶龙格-库特算法和MATLAB-simulink进行计算仿真，去讨论大气摄动对卫星轨道的影响.

1 大气摄动下轨道模型

下面的讨论中，地球视为密度均匀的圆形球体，大气密度近似采用指数分布，采用地心惯性坐标系Oxyz，给出相应数学模型.

在地心惯性坐标系下，大气摄动下轨道模型为：

其中

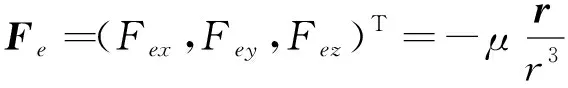
为地球中心引力；

为大气摄动力，且其中

t：时间(s)；

r：r=(x,y,z)T为卫星位置矢量(km)；

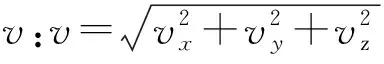
μ：μ=398 601.19为地心引力常数(km3/s2)；

Cd：大气阻尼系数，一般取为1.5～2.3[2]，这里取为Cd=2；

S/M：卫星面质比，S为有效(相对阻力而言)截面积，M为卫星质量，一般卫星的面质比在2～20(m2/t)[3]，这里取S/M=10-8(km2/kg)；

va：大气在Oxyz坐标系中的运动速度(km/s)；

V：卫星相对于大气的运动速度，V=v-va，空间大气并非处于静止状态，大气有旋转，而且情况复杂.记ωa为大气旋转角速度，ne为地球自转角速度.根据多年来卫星资料，发现大气旋转速率随高度变化而不同，大气这一旋转机制还不清楚.多年的卫星资料得到的变化情况[4]，在卫星距地面高度为325～600 km时，ωa/ωe呈近似线性减小变化，从1.22下降到0.82，这里取ωa/ωe=1.此时有[2]va=ne(-y,x,0)TV=(vx+ney,vy-nx,vz)T；

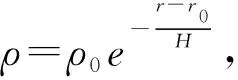
取初始条件为：

r(0)=(7 120.64,176.842,112.678)T

v(0)=(-0.172 005,3.168 71,6.785 77)T

记

X=(x,y,z,vx,vy,vz)T,f(X,t)=(vx,vy,vz,Fex+Fdx,Fey+Fdy,Fez+Fdz)T

则上述模型可表为向量微分方程的初值问题：

(1)

2 模型离散化算法

模型(1)式是一个一阶向量形式的非线性微分方程，它没有解析解，只能求数值解.记Δt为采样周期，Xi=X(ti)(i=0,1,2,…,N),下面采用四阶龙格-库特算法把该模型进行离散化.

其中

k1=f(Xi-1,ti-1)

k4=f(Xi-1+k3,ti-1+Δt)

X0=X(0)

(i=1,2,…,N)

3 模型求解

下面取Δt=240 s，仿真时间区间为0～12 000 s,利用Matlab-simulink求解.相应的simulink模块参看图1，计算结果数据参看表1，轨道计算结果图形参看图2，卫星到地心的距离参看图3.

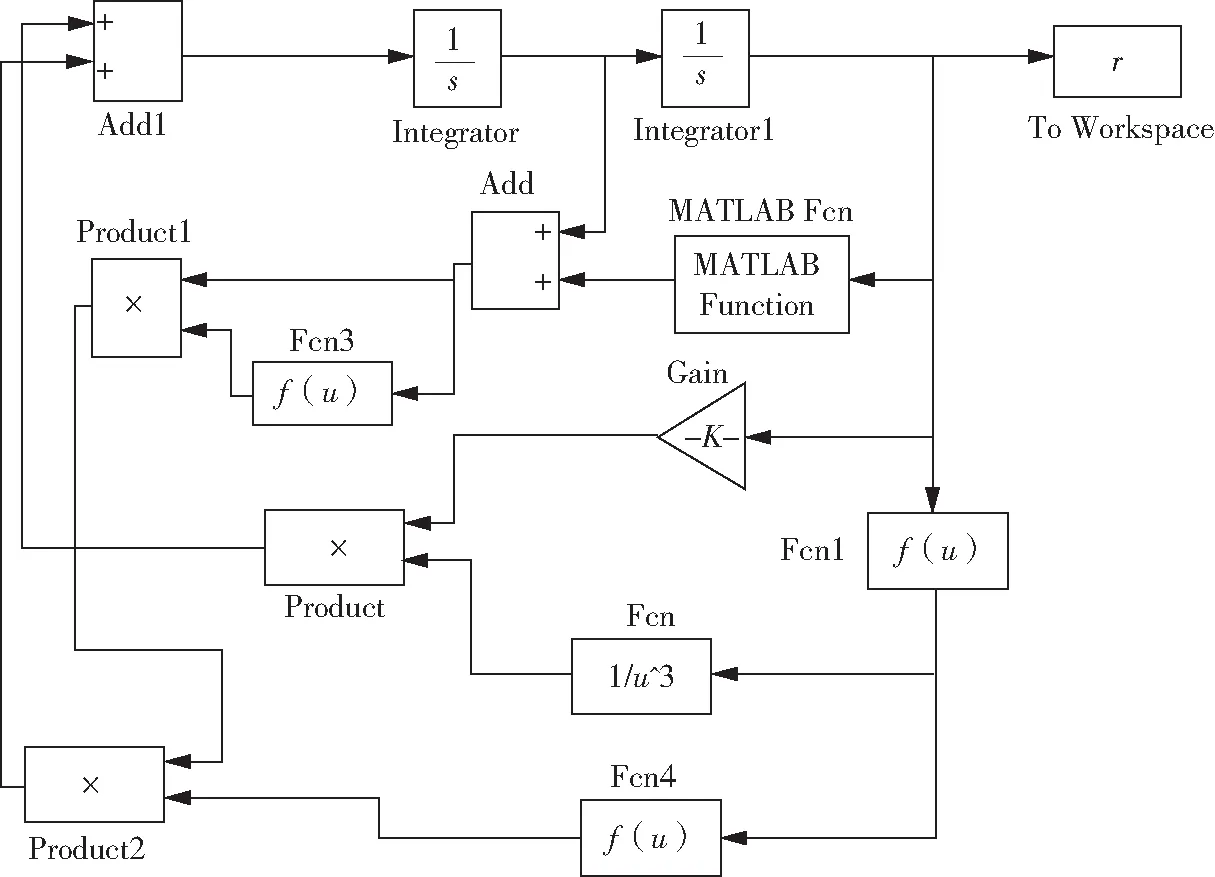
图1 Simulink模块

表1 卫星位置坐标及到地心的距离

续表

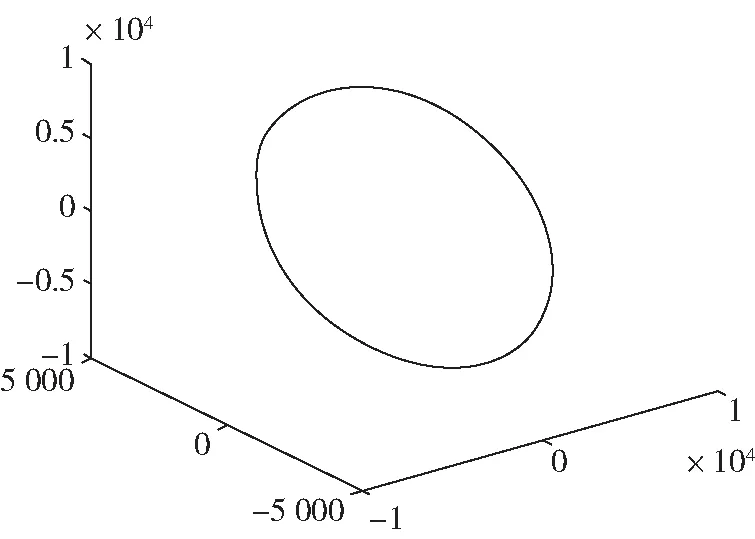
图2 卫星轨道

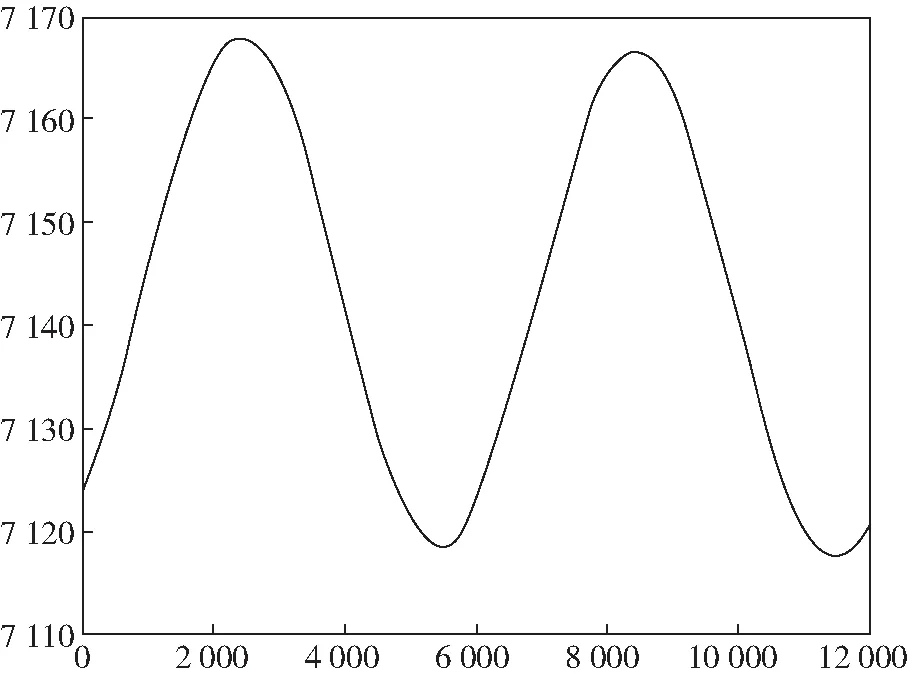
图3 卫星到地心的距离

理想的二体轨道应该是卫星在一个不变的轨道上运行.在大气阻力作用下，在仿真时间段为0～12 000 s的时间内卫星大约两圈.第一圈的远地点：7 168.05 km，近地点：7 118.56 km；第二圈的远地点：7 166.75 km，近地点：7 117.32 km；第二圈比第一圈轨道的远地点减小了1.3 km，近地点减小了1.24 km.

4 结论

实际卫星飞行过程中，也受到其他要素(地球非球形、日月引力、太阳光压等)的影响，以上只考虑了地球中心引力和大气密度、大气旋转的作用下，建立了数学模型，利用四阶龙格-库特算法和MATLAB-simulink进行了模型求解.从理论上讲四阶龙格-库特算法精度(o(Δt4))有一定的方法误差，且由于大气密度变化十分复杂,不但与高度有关，而且还与昼夜、季节等要素有关，另外大气的旋转机制也不十分清楚，只是做了一些近似处理.通过对结果的分析得到了大气对轨道的影响，卫星轨道随着时间的推移，使得轨道高度逐渐变小，在两圈的仿真中，远地点就减小1.3 km，近地点减小了1.24 km，这样随着时间的推移，卫星轨道将会逐渐变小.